随着互联网技术的发展,电子商务极大地影响了传统消费模式和消费行为。中国互联网络信息中心(CNNIC)发布第36次中国互联网络发展状况统计报告显示,截至2015年6月,我国网民规模达6.68亿,互联网普及率为48.8%,中国网络购物用户规模达到3.74亿。相对传统行业的客户管理,电子商务的客户流失率高达80%。有研究表明,保持现有客户比获取新客户的成本低得多,一般可节约4~6倍。如果用户保持率增加5%,会为运营商带来85%的利润增长。因此在准确识别出电子商务流失客户的同时,若能加强对非流失高价值客户的识别,将为后期客户保持提供基础。
现有客户流失预测研究中,主要包括基于传统统计学的预测、基于人工智能的预测、基于统计学习理论的预测、基于组合分类器的预测和基于仿生学算法的预测。Renjith[1]提出用Logistic回归来预测电子商务中流失的客户,再借助机器学习方法提出个性化客户保留策略。文献[2- 4]主要研究支持向量机的改进。张秋菊等[5]将自组织数据挖掘中的客观系统分析算法(OSA)和改进分组数据处理网络(GMDH)集成起来进行电子商务客户流失预测。近年来组合分类器也被应用到了客户流失预测研究中,它利用各个子分类器之间的互补性,按照一定的方式将各子分类器进行融合,以提高其性能。组合分类器包括Schapire提出的Boosting算法[6]和Breiman提出的Bagging算法[7]。AdaBoost是最优秀的Boosting算法之一,在实践中得到了很好的推广和应用。应维云[8]提出LDA boost方法,通过将线性判别LDA引入Boosting算法框架中,应用到商业银行的客户流失预测中。Liu等[9]为了平衡数据,对少数类赋予一个较大的权值,对AdaBoost改进后应用到客户流失预测。张玮等[10]将CART和自适应Boosting集成模型应用于通信企业客户流失预测,对离网客户预测具有一定的准确性。
随着电子商务交易量快速增加和市场的激烈竞争,为了满足客户日益增长的个性化需求,需要通过差异化服务和针对性策略吸引客户,提高客户忠诚度,电子商务领域也需要像传统的市场营销一样进行客户细分。另一方面,电子商务客户流失呈非线性变化、客户类别是非对称的,电子商务客户流失数据具有典型样本不平衡性,即流失样本数目明显比非流失样本数目多得多。目前对不平衡的电子商务客户流失数据进行平衡的研究较少。本文提出基于客户细分的电子商务客户流失预测研究,用改进SMOTE进行数据平衡,再用AdaBoost算法进行预测,与未细分前的预测结果对比;同时与BP神经网络、支持向量机[11](support vector machine, SVM)和分类加权支持向量机[12](class weighted support vector machine, CW-SVM)3种成熟的客户流失预测方法的预测效果进行对比分析。
1 电子商务客户细分 1.1 客户细分客户细分是客户关系管理价值实现的基础,是进行客户关系管理的关键步骤,也是更高效地进行针对性营销活动的重要前提。依据著名的帕累托原则,企业80%的利润是由20%的客户创造的,有50%的利润被底部30%的非盈利客户损失掉。而要进行客户细分首先要识别和挖掘客户价值,企业若能聚焦客户实际价值来分配资源针对性进行市场营销,便能更好地提高核心竞争力。
随着电子商务的快速发展,通过网络进行的企业商务活动更多体现的是实时和交互的特点,从而也使得原本以产品为中心的经营模式转变为以客户为中心,客户成为企业获得利润和竞争优势的重要资源。而电子商务客户流失率较高,企业若要与客户建立长期的合作联盟关系,发展稳定持续的客户关系,将会面临很多挑战。电子商务客户群广泛而复杂,其价值参差不齐。如何准确识别高价值客户,做好流失预测并提前挽留成为电子商务领域较为关注的热点。另一方面,客户价值的评价有利于企业在众多的消费者当中识别出有价值的客户,并根据客户价值的不同实行不同的客户管理,使企业有限的资源发挥最大的功效。购买价值作为电子商务客户主要的显性价值被文本选择为考察客户价值主要的衡量指标,购买量的大小直接关系到企业产品或服务的销售量,是实现企业利润目标的保证,也是客户价值大小的最为直接的体现。在此主要利用历史交易数据鉴定客户的价值高低,以此为依据进行客户细分。
客户细分研究不断得到理论和实践方面的发展和创新,一些聚类分析算法在这方面已经得到了长足的应用。赵铭等[13]用K-means算法对商业银行的基金理财客户交易行为数据进行了分类。徐翔斌等[14]在传统零售行业客户细分的RFM模型上,引入总利润属性,创建RFP模型,使用数据挖掘K-means算法对某电子商务企业客户进行聚类分析。Brito等[15]用实例证明,应用K-Medoids更好地了解了电子商务客户偏好,使企业能更好地响应客户需求,提高竞争力。有研究表明,对于大量数据集的处理,K-Medoids算法较K-means算法更高效[16]。本文选择K-Medoids聚类算法对电子商务客户进行细分。
1.2 K-Medoids聚类算法为了实现对数据对象的分类,人们提出了许多不同的聚类算法。K-means算法是最为经典的基于划分的聚类方法,是十大经典数据挖掘算法之一。其类中心的计算是对调整后的新类使用平均值的方法,因此容易受到离群点的影响。为了克服K-means算法对离群点的敏感性,本文选择K-中心点聚类(K-Medoids)方法作为细分的方法,不采用类中对象的均值作为新类中心,而是在每个类中选出一个实际的对象来代表该类。其余的每个对象聚类到与其最相似的代表性对象所在的类中。该算法可以克服K-均值算法容易陷入局部最优的缺陷。围绕中心点的划分(partitioning around medoids,PAM)是最早提出的K-Medoids算法之一[17]。该算法用数据点替换的方法获取最好的聚类中心。本文利用该聚类算法对电子商务客户进行细分,识别出高价值客户。
2 电子商务客户流失预测模型的建立 2.1 电子商务客户流失的定义客户流失是指企业原有的客户终止继续购买企业商品或接受企业服务,转而接受竞争对手的商品或服务[18]。电子商务客户流失则是一般性客户流失的一种,即由于某些原因电子商务客户离开当前为其所提供产品或服务的电子商务企业。电子商务客户流失是一种非契约关系情景下的客户流失。在非契约关系下,这种企业–客户关系即便发生了终止也很难被企业提前察觉到。对于电子商务企业来说,能够准确预测即将流失的高价值客户群体很有现实意义,同时对没有流失的客户购买习惯进行研究以便更好地保留该类客户群体,从而减少企业为开拓新客户付出更多的成本,提高企业客户管理效率和客户忠诚度。
电子商务客户流失预测原理是对在一段时间内的电子商务客户数据进行收集,通过对电子客户购买行为进行分析,建立电子商务客户流失预测模型,进而给出电子商务客户流失挽留措施,减少客户流失,另一方面识别出高价值非流失电子商务客户,做好客户保持工作。
本文应用改进后SMOTE+AdaBoost对聚类后高价值客户进行流失预测,将细分前后的预测精度进行对比。同时为了说明该预测算法的有效性,最后与BP神经网络、SVM、CW-SVM 3种不同客户流失预测算法的预测结果进行对比。具体流程框架如 图1。
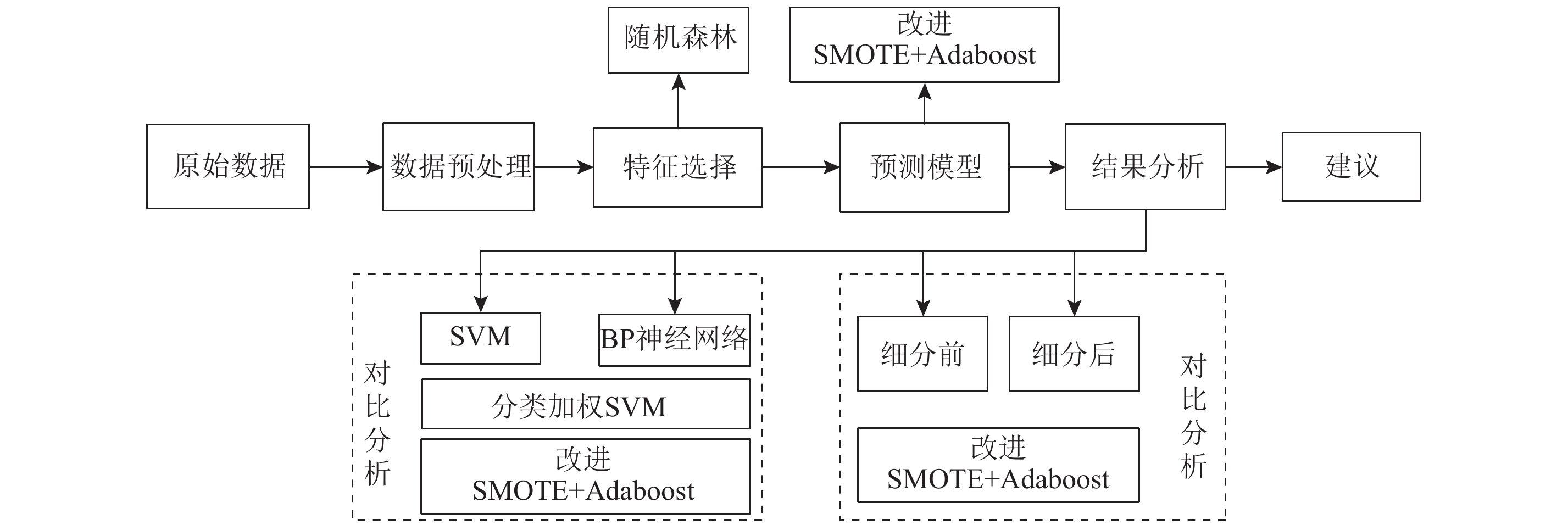
|
图 1 基于客户细分的电子商务客户流失预测系统框架图 Fig. 1 The system frame of e-commerce customer churn prediction based on customer segmentation |
非平衡数据集(imbalanced data sets)是指数据集中某一类或者某些类的样本量远远大于其他类,多数类称为负类,少数类称为正类。不平衡率(imbal-ancerate)是测度非平衡数据集不平衡程度的重要指标,它是正负两类样本量的比率。针对不平衡数据的预处理,主要目的是降低数据集的不平衡程度,人为地增加少数类的样本(over sampling,过采样),人为地减少多数类的样本(under sampling,欠采样)等。SMOTE[19](synthetic minority oversampling technique)是通过人工合成新的少数类样本以降低类别的不平衡性,其基本思想是:在相距较近的少数类之间插入少数类虚拟样本。对少数类的每个样本 X i ,搜索其 k个最邻近,随机选取这 k个最近邻中的任意 m个近邻点 Y ij ( j=1, 2, … m)。按式(1)合成新的少数类样本 P j ( j=1, 2, … m):
| $\quad\quad {P_j} = {X_i} + {\rm{rand}}(0,1) \times ({Y_{ij}} - {X_i})\text{。}$ | (1) |
其中rand(0, 1)表示区间在(0, 1)之间的一个随机数。将新合成少数类样本合并到原数据集中,使不平衡率降低,同时可以减少分类器过拟合现象。然而SMOTE算法在合成新样本的过程中没有充分考虑多数类近邻样本的信息,具有一定的盲目性,同时不能对合成样本数量进行精细控制。
一般来说,非平衡数据集的欠采样效果较过采样好[20]。因此本文提出改进SMOTE,将过采样和欠采样方式有机结合。通过欠采样减少多数类的比例,直至多数类和少数类成一定比例。在采样前,设定最终合成数据集中欠采样比( N under)和过采样比( N over)。欠采样将从多数类样本数据中随机抽取多数类样本数,结合SMOTE人工合成少数类样本,通过设定的采样比平衡数据集。过采样将产生新少数类为原少数类的 N over,而欠采样将依据新生成的少数类和欠采样比确定最终的多数类,即为新产生的少数类 S× N over的 N under。若原始数据集中,少数类样本数为 S,则最后多数类样本将变为 S× N over× N under,而少数类样本将为 S+ S× N over。以此来控制正负样本数量和训练模型的规模,提高算法效率和预测精度。
2.3 AdaBoostBoosting,也称为增强学习或提升法,是一种重要的集成学习技术,能够将预测精度仅比随机猜度略高的弱学习器增强为预测精度高的强学习器。AdaBoost算法是Freund等提出的一种组合算法,是最优秀的Boosting算法之一。它利用一种自适应的重采样技术,对错分的样本增大采样概率重新采样,通过加强对错分样本的学习来提高分类精度。具体算法如下,设训练样本集
1) 初始化权重:
2)DO FOR t=1, ..., T (弱分类器数量)。
①用弱学习算法
L训练得到弱学习分类器:
②计算
| $\quad\quad {\varepsilon _t} = \sum\limits_{i = 1}^n {\omega _i^t} I\left[ {{h_t}({x_i}) \ne {y_i}} \right]{\text{。}}$ | (2) |
ε
t
为第
t个弱分类器的带权分类误差值,
| $\quad\quad I\left[ {{h_t}({x_i}) \ne {y_i}} \right] = \left\{ \begin{align}& 0,\;\;\;\;{h_t}({x_i}) = {y_i} ;\\& 1,\;\;\;\;{h_t}({x_i}) \ne {y_i}\text{。}\end{align}\right.$ | (3) |
从公式(2)和(3)看带权分类误差 ε t 和分类器在样本上的误差值和样本集中每个样本的权重相关;弱分类器 h t 的权重 α t 与其本身的带权分类误差相关,即
| $\quad\quad {\alpha _t} = \frac{1}{2}\ln [(1 - {\varepsilon _t})/{\varepsilon _t}]\text{。}$ | (4) |
③调整样本权值:
| $\quad\quad \omega _i^{t + 1} = \frac{{\omega _i^t}}{{{z_t}}} \times \left\{ \begin{align}& {{\rm{e}}^{\alpha _t}},\;\;\;{h_t}({x_i}) \ne {y_i};\\& {{\rm{e}}^{ - {\alpha _t}}},\;\;{h_t}({x_i}) = {y_i}\text{。}\end{align}\right.$ |
z t 为归一化因子。如果该分类器在该样本上分类正确,则降低该样本的权值,若分类错误则提高该样本的权值。
3)循环结束后,组合分类器为
AdaBoost算法给错分样本更大的权重,根据加权错误率最小来选取新分类器。基于改进SMOTE和AdaBoost的电子商务客户流失预测模型,通过采样比确定合成样本中正负样本的数量,控制模型的训练时间,将平衡后的数据集输入集成学习算法AdaBoost来训练弱分类器,经过多次迭代,提高流失客户和非流失客户的预测精度。
3 实证研究 3.1 不平衡数据集评价指标传统的评价指标采用的混淆矩阵,如 表1所示,其中,TP为正类样本判为正类的个数,TN为负类样本判为负类的个数,FN、FP分别为判决错误的实际正类和负类样本数目。
| 表 1 二分类混淆矩阵 Tab. 1 Binary classification confusion matrix |
传统分类学习中,采用分类精度作为预测模型分类性能的指标。如公式(5)。而在一个二分类不平衡的数据集中,分类精度却因其更倾向于预测多数类而无法准确衡量分类器的性能[21]。在不平衡数据分类评价标准中,主要应用ROC[22](receiver operating characteristics curve)、AUC[23](area under the ROC curve)、G-mean准则、F-value准则来评价模型。ROC曲线将真正率(TPR)作为纵轴,将假正率(FPR)作为横轴。因此少数类的性能提升以多数类的性能损失为代价。而在二分类电子商务客户流失预测中,希望流失客户预测精度较高的情况下,非流失客户的预测精度也能有较好的提升,因此ROC曲线上越靠近坐标系左上角预测效果越好。
| $\quad\quad {\rm{Accuracy}} = \frac{{{\rm{TP}} + {\rm{TN}}}}{{{\rm{TP}} + {\rm{TN}} + {\rm{FN}} + {\rm{FP}}}}\text{。}$ | (5) |
真正率(true positive rate)/灵敏度(sensitivity)/查全率(recall)为
| $\quad\quad {\rm{TPR}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}}\text{;}$ | (6) |
假正率(false positive rate)为
| $\quad\quad {\rm{FPR}} = \frac{{{\rm{FP}}}}{{{\rm{FP}} + {\rm{TN}}}}\text{;}$ | (7) |
特异性(specificity)为
| $\quad\quad {\rm{Specificity}} = \frac{{{\rm{TN}}}}{{{\rm{TN}} + {\rm{FP}}}}\text{;}$ | (8) |
少数类预测/查准率(precision)为
| $\quad\quad {\rm{Precision}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}}}}\text{。}$ | (9) |
考虑到ROC曲线不能很好地定量化分类效果的性能,一般用其下面的面积AUC作为量化指标,AUC越大,说明ROC曲线下面的面积越大,分类器效果越好。
G-mean准则用灵敏度(sensitivity)考察少类分类性能,用特异性(specificity)考察多类分类性能。G-mean避免过度拟合负类的重要度量[24]。其定义为
| $\quad\quad {\rm{G}} {\tiny{-}}{\rm{mean}} = \sqrt {{\rm{sensitivity}} \times {\rm{specificity}}} \text{。}$ | (10) |
F-value准则主要组合了查全率和查准率指标,较高的F-value意味着分类器在正类上具有更好的性能,定义为
| $\quad\quad {\rm{F}} {\scriptstyle-}{\rm{value}} = \frac{{(1 + {\beta ^2}) \times {\rm{recall}} \times {\rm{precision}}}}{{{\beta ^2} \times {\rm{recall}} + {\rm{precision}}}}\text{。}$ | (11) |
其中, β表示recall与precision的相对重要性,通常取 β=1。
3.2 样本选择本文采用的数据来自于某B2C电子商务网站,主营办公文具用品。以2015年1月为实证研究的起始,观测终止时间为2015年10月。选取1~5月内首次在该网站购买商品的客户消费数据进行分析和预测,该数据集主要为客户消费明细。其中定义在观测期未来的5个月(6~10月)内若有继续消费,即为非流失客户;在未来的5个月内没有继续消费,即标记为流失客户。通过对数据进行缺失值处理、数据变换和数据规约预处理后,最后得到1~5月内首次在该网站购买商品的3935条客户消费数据。在观测期结束后,3935名客户中,3474名客户流失(约占88%),461名客户未流失。综合考虑电子商务客户流失的各种影响因素,参考国内外电子商务客户流失相关文献,并考虑解释变量数据的可获得性,最终确定出客户白天购买次数、晚上购买次数、深夜购买次数、购买次数、购买金额、购买商品件数、购买商品种类、返点积分、信用等级、支付积分、客户编号11个指标作为本文研究的待选解释变量。
3.3 客户细分本文选择主成分分析法对主要细分指标进行筛选。主成分分析法的目的就是使用较少的指标尽可能多地描述原来指标的信息量,从而减少实际操作中的工作量。在实践中,考虑到既要保持原始数据的主要信息又能很好地进行属性约简,最常见的主成分个数提取方法是被提取的前 m个主成分的累积方差贡献率需大于等于85%。本文选择客户白天购买次数、晚上购买次数、深夜购买次数、购买次数、购买金额、购买商品件数、购买商品种类、返点积分、信用等级、支付积分10个数值变量作为原始变量集,运用SPSS对原数据进行主成分分析,选择输入聚类细分的变量成分。
从各变量的相关系数矩阵看,晚上购买次数和白天购买次数有较强的负相关性,购买商品件数和购买商品种类、购买金额和返点积分有较强的相关性,说明有部分信息重叠。而一般来说主成分个数的提取规则是累计方差贡献率大于等于85%的前
N个主成分。本文中,6个主成分的累计方差贡献率为86.7%。根据SPSS输出的因子载荷进行分析处理,对因子载荷矩阵的第
k列的每个元素分别除以第
k个特征根的平方根
| 表 2 主成分系数矩阵 Tab. 2 Principal component coefficient matrix |
根据上文属性约简后,选择以上分析的6个主成分作为聚类分析的输入变量。本章节结合电子商务客户数据的特征,选择K-Medoids聚类法为细分方法。为了得到最佳的聚类数,参考Kaufman[25]等提出的平均轮廓宽度标准(average silhouette width criterion)来衡量最终聚类结果的优劣。最终选择最大平均轮廓宽度值对应的 k=3为最佳聚类数。
将客户聚成3大类,细分后类Ⅰ有371名客户,其中未流失72人,流失299人,流失率达到80%;而类Ⅱ总客户1 565名,流失1 401名,流失率为89%;类Ⅲ总客户数1 999,非流失225,流失1 774,流失率为88%。
根据以上聚类结果,结合构成6个主成分PC1~PC6的各个变量上对应的系数大小,选择购买金额、购买商品件数、购买商品次数,返点积分、支付积分和信用等级6个与客户消费行为密切相关的指标进行客户类别识别。客户Ⅰ的消费次数、消费金额和买家信用等级都较高,客户数量仅为总客户数的10%,其总购买金额占总金额的30%,因此识别其为高价值客户群体;而客户Ⅲ的购买金额、信用等级都相对较低,客户数量为总客户数的30%,其购买金额却只占总金额的10%,因此为较低价值客户。客户Ⅱ处于两者之间。
对细分后高价值客户和细分前客户进行客户流失预测研究。首先对建模输入特征变量进行选择:以随机森林算法为基本工具研究Wrapper特征选择方法,利用随机森林分类器的分类准确率作为特征可分性判据,基于随机森林算法本身的变量重要性度量进行特征重要性排序选择。在R语言中random-Forest()函数中的importance参数用来提取随机森林模型中各个变量的重要性的度量结果。最后选择关键属性集{购买金额、购买商品件数、返点积分和支付积分}作为输入,客户流失状态为目标变量,用1表示客户流失,0表示客户未流失。
用改进SMOTE+AdaBoost建模时,首先对原样本数据3 935(461非流失,3 474流失)名客户进行平衡处理,通过改进SMOTE对电子商务不平衡数据集进行平衡,改进SMOTE算法中邻域 k设置为5,在R语言环境实现,设置欠采样比 N under为1.5,过采样比 N over为2,对细分前后客户数据分别进行改进SMOTE方法平衡后,得到平衡后数据集如 表3。将平衡后数据集分别输入AdaBoost模型预测,其中弱分类器的个数即迭代次数设置为100。
| 表 3 平衡前后数据集 Tab. 3 The balanced data set |
实验中采用十折交叉检验 (10-fold cross validation)的测试方法,将数据分为10份,9份作为训练集,1份作为测试集,将10次实验得出的测试结果的均值作为该算法的最终评价结果。将平衡后的数据集输入AdaBoost算法训练,与SVM、BP神经网络和分类加权支持向量机(CW-SVM)相对比,不同方法得到各项评价指标结果如下。其中分类加权支持向量机建模时,考虑到非流失类客户误分代价远高于流失类客户误分代价,为提高非流失类客户的预测精度,朱帮助等[5]在建模时将非流失类客户数据复制数次,使其数据量与流失类客户数量大致相当。复制次数 C=流失客户量/非流失客户量–1,若 C不为整数,则四舍五入取整。因此在CW-SVM预测模型中,将非流失客户的权重设为流失客户权重的 C倍, C=流失客户量/非流失客户量。
图2为不同算法在细分前所有电子商务客户预测中Specificity、Sensitivity、accuracy、G-mean、F-value和AUC的对比图,从图可见,SVM、BP神经网络未对不平衡数据集进行处理,得到的Specificity和accuracy较高,由于电子商务客户流失数据的不平衡性,分类器往往会牺牲少数类(非流失)的性能,在多数类(流失)上获得较高的准确率,即Specificity较高,且分类器的平均准确率将很高。因此仅用准确率来评价不平衡数据集的分类效果具有片面性。
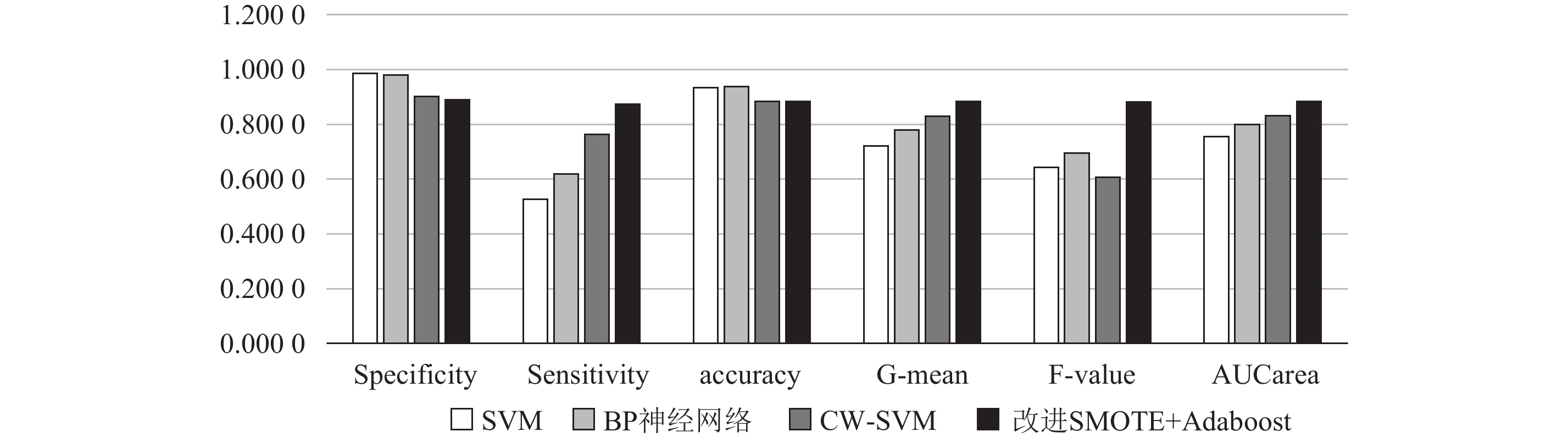
|
图 2 不同方法对细分前电子商务流失客户预测性能指标对比 Fig. 2 Performance index of e-commerce customers churn prediction before segmentation by different methods |
从不平衡数据集主要评价指标G-mean、F-value和AUC看,改进SMOTE+AdaBoost方法在电子商务客户流失预测中效果最佳,其次是分类加权支持向量机(CW-SVM)方法,其考虑了类权重,在不平衡的电子商务流失预测中相比于SVM和BP神经网络效果较好。因此在电子商务客户流失预测中,考虑数据不平衡性的预测方法较未对数据进行平衡处理的方法预测效果更好,能更有效地提高对非流失客户的预测精度,即灵敏度(Sensitivity)。
CW-SVM与改进SMOTE+AdaBoost的ROC曲线如 图3,ada表示改进SMOTE+AdaBoost预测方法,ksvm表示CW-SVM预测方法。在对电子商务客户流失的预测中,改进SMOTE+AdaBoost预测效果明显比考虑类权重的支持向量机好。
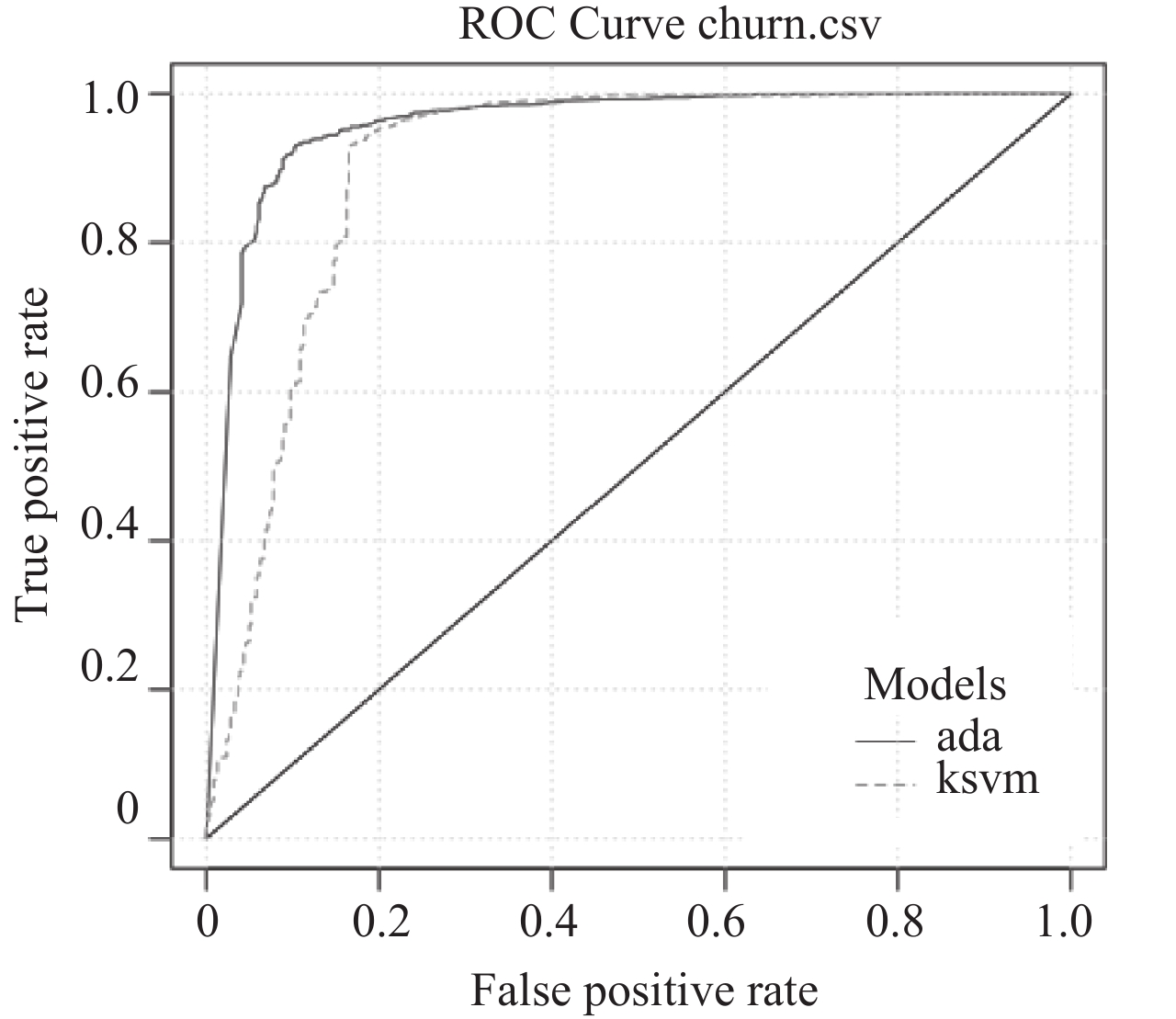
|
图 3 CW-SVM和改进SMOTE+AdaBoost预测方法ROC曲线 Fig. 3 The ROC curve of CW-SVM and improved SMOTE + AdaBoost |
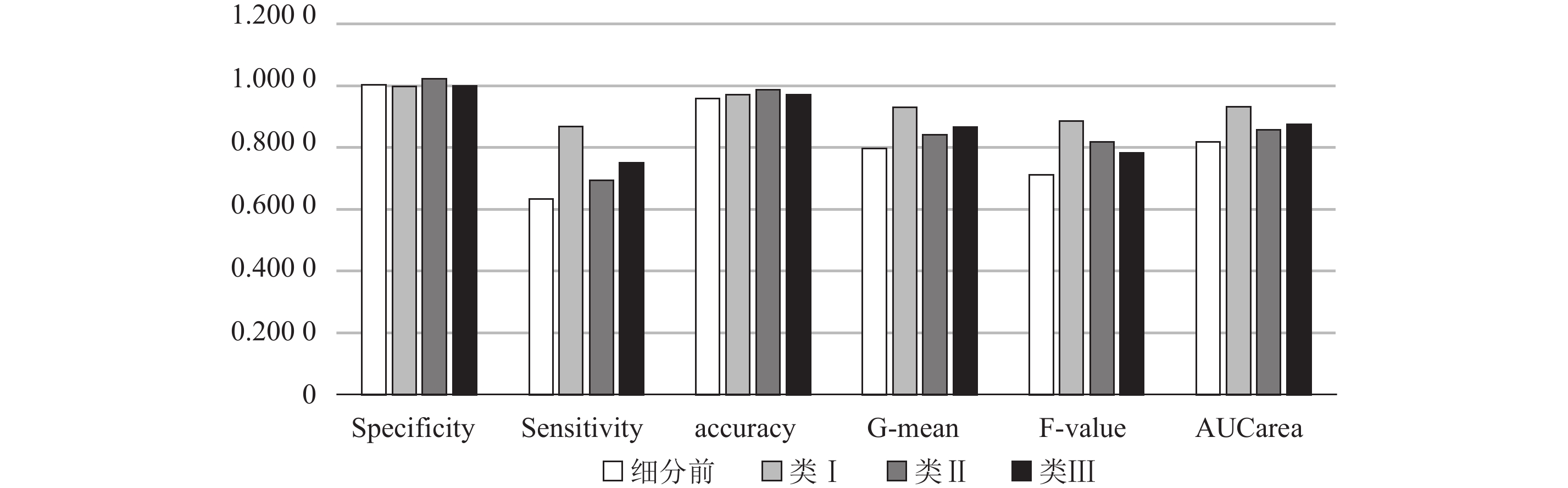
对细分后3类客户,分别用BP神经网络、SVM、CW-SVM和改进SMOTE+AdaBoost 4种不同方法进行客户流失预测,与客户细分前相比,3类客户各项指标均有较大的提高,其中改进SMOTE+AdaBoost方法在G-mean、F-value和AUCarea这3个衡量不平衡数据集分类效果的指标上有很大提升,该方法对不同客户群体的各项指标对比如 图4。未对数据集进行平衡的BP神经网络方法对细分前后客户的各项评价指标如 图5,其主要提升在于对少数类的预测精度和整体AUC。
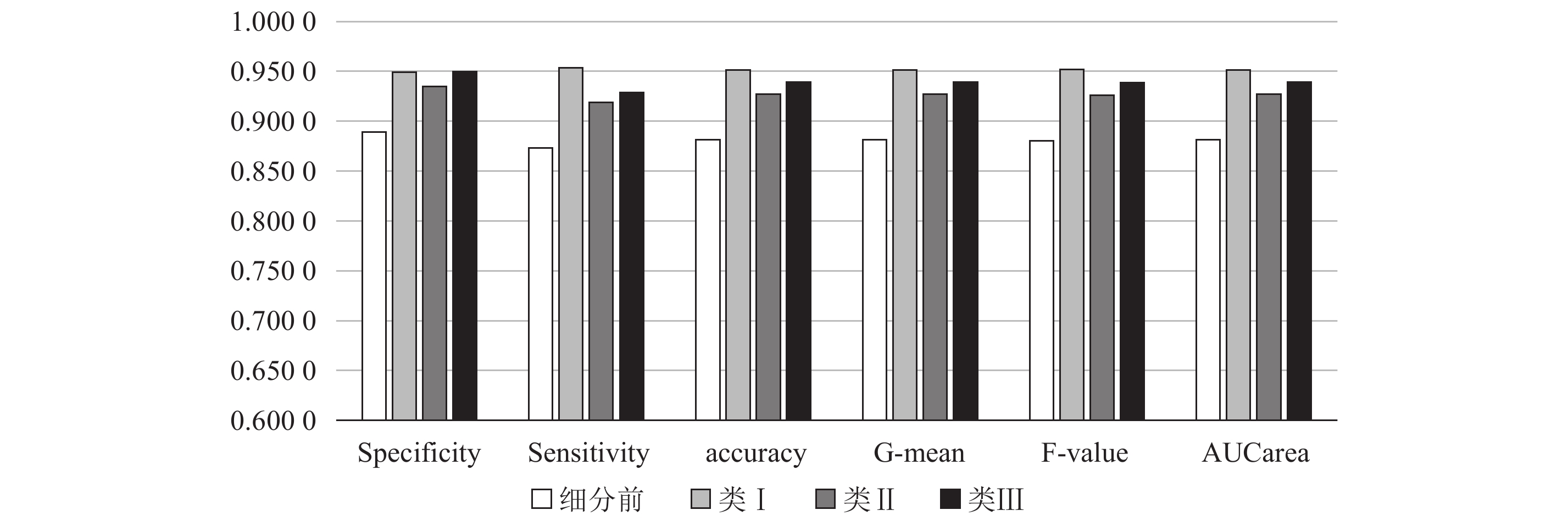
|
图 4 改进SMOTE+AdaBoost方法对细分前后客户各项指标 Fig. 4 The indicators of improved SMOTE + AdaBoost for the original customer and segmented customer |
|
图 5 BP神经网络方法对细分前后客户各项指标 Fig. 5 The indicators of BP neural network for the original customer and segmented customer |
从以上分析可知,客户细分后改进SMOTE+AdaBoost方法在各类上对流失客户和非流失客户的预测精度和G-mean、F-value及AUCarea指标都有较大提高,而高价值客户群体类Ⅰ的预测效果明显比细分前好。客户细分能有效识别出高价值客户群体,并提高对流失客户和非流失的预测准确性,从而提高整体预测效果。
4 结论考虑到电子商务客户流失数据的不平衡性,客户价值相差较大,在提高对流失客户预测准确性的同时,也希望对非流失客户的预测能有较好的效果,为后期客户保持工作提供客户基础。本文提出基于客户细分后的改进SMOTE+AdaBoost方法,首先通过聚类对电子商务客户进行细分,识别出不同价值客户,再通过欠采样和SMOTE结合的采样技术在有效增加少数类的样本量的同时减少多数类样本量,通过采样比平衡正负类数据,降低数据集的规模,同时结合AdaBoost算法提高分类器的分类精度。实验结果表明,在客户细分后各预测方法的预测效果有较大提高,用不同方法对各项评价指标进行对比,对数据进行不平衡性处理的预测方法CW-SVM和改进SMOTE+AdaBoost能明显提高对非流失客户的预测精度,改进SMOTE+AdaBoost方法能更准确识别出流失和非流失客户。这将为下一步客户保持和挽留工作提供基础。
| [1] | RENJITH S. An integrated framework to recommend personalized retention actions to control B2C E-commerce customer churn[J]. International Journal of Engineering Trends and Technology, 2015, 27(3): 152-157. DOI: 10.14445/22315381/IJETT-V27P227. |
| [2] | JU C H, LU Q B, GUO F P. E-commerce customer churn prediction model combined with individual activity[J]. Systems Engineering-Theory & Practice, 2013, 33(1): 141-150. |
| [3] |
朱帮助. 基于SMC-RS-LSSVM的电子商务客户流失预测模型[J].
系统工程理论与实践, 2010, 30(11): 1960-1967.
ZHU Bangzhu. E-business customer churn prediction based on integration of SMC, rough sets and least square support vector machine[J]. Systems Engineering-Theory & Practice, 2010, 30(11): 1960-1967. DOI: 10.12011/1000-6788(2010)11-1960. |
| [4] | YU X B, GUO S S, GUO J. An extended support vector machine forecasting framework for customer churn in e-commerce[J]. Expert Systems with Applications, 2011, 38(3): 1425-1430. DOI: 10.1016/j.eswa.2010.07.049. |
| [5] |
朱帮助, 张秋菊, 邹昊飞, 等. 基于OSA算法和GMDH网络集成的电子商务客户流失预测[J].
中国管理科学, 2011, 19(5): 64-70.
ZHU Bangzhu, ZHANG Qiuju, ZOU Haofei. E-business customer churn prediction based on integration of objective system analysis and group method of data handling network[J]. Chinese Journal of Management Science, 2011, 19(5): 64-70. |
| [6] | SCHAPIRE R E. The strength of weak learnability [C]// Foundations of Computer Science, 1989. 30th Annual Symposium on. IEEE, 1989: 197-227. |
| [7] | BREIMAN L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
| [8] |
应维云, 蔺楠, 谢雅雅, 等. 用LDA Boosting算法进行客户流失预测[J].
数理统计与管理, 2010, 29(3): 400-408.
YING Weiyun, LIN Nan, XIE Yiayia. Research on the LDA boosting in customer churn prediction[J]. Journal of Applied Statistics & Management, 2010, 29(3): 400-408. |
| [9] | LIU M, QIAO X Q, XU W L. Three categories customer churn prediction based on the adjusted real adaBoost[J]. Communication in Statistics- Simulation and Computation, 2011, 40(10): 1548-1562. DOI: 10.1080/03610918.2011.589732. |
| [10] |
张玮, 杨善林, 刘婷婷. 基于CART和自适应Boosting算法的移动通信企业客户流失预测模型[J].
中国管理科学, 2014, 22(10): 90-96.
ZHANG Wei, YANG Shanlin, LIU Tingting. Customer churn prediction in mobile communication enterprises based on CART and Boosting algorithm[J]. Chinese Journal of Management Science, 2014, 22(10): 90-96. |
| [11] | SUYKENS J A k, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300. DOI: 10.1023/A:1018628609742. |
| [12] |
应维云, 覃正, 赵宇, 等. SVM方法及其在客户流失预测中的应用研究[J].
系统工程理论与实践, 2007, 27(7): 105-110.
YING Weiyun, QIN Zheng, ZHAO Yu. Support vector machine and its application in customer churn prediction[J]. Systems Engineering--Theory & Practice, 2007, 27(7): 105-110. |
| [13] |
赵铭, 李雪, 李秀婷, 等. 基于聚类分析的商业银行基金客户的分类研究[J].
管理评论, 2013, 7: 38-44.
ZHAO Ming, LI Xue, LI Xiuting. Research on the classification of commercial banks’ fund clients based on clustering analysis[J]. Management Review, 2013, 7: 38-44. DOI: 10.3969/j.issn.1008-3448.2013.06.005. |
| [14] |
徐翔斌, 王佳强, 涂欢, 等. 基于改进RFM模型的电子商务客户细分[J].
计算机应用, 2012, 32(5): 1439-1442.
XU Xiangbin, WANG Jiaqiang, TU Huan. Customer classification of E-commerce based on improved RFM model[J]. Journal of Computer Applications, 2012, 32(5): 1439-1442. |
| [15] | BRITO P Q, SOARES C, ALMEIDA S. Customer segmentation in a large database of an online customized fashion business[J]. Robotics and Computer-Integrated Manufacturing, 2015, 36: 93-100. DOI: 10.1016/j.rcim.2014.12.014. |
| [16] | VELMURUGAN T, SANTHANAM T. Computational complexity between K-means and K-medoids clustering algorithms for normal and uniform distributions of data points[J]. Journal of Computer Science, 2010, 6(3): 363-368. DOI: 10.3844/jcssp.2010.363.368. |
| [17] | WANG D, THOMAS S G, WANG k L. Finding groups in data, an itroduction to cluster analysis[J]. Applied Physics Letters, 1997, 70(12): 1593-1595. DOI: 10.1063/1.118625. |
| [18] | HADDEN J, TIWARI A, ROY R. Computer assisted customer churn management: State-of-the-art and future trends[J]. Computers & Operations Research, 2007, 34(10): 2902-2917. |
| [19] | CHAWLA N V, BOWYER K W, HALL L O. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357. |
| [20] | DRUMMOND C, HOLTE R C. C4. 5, class imbalance, and cost sensitivity: why under-sampling beats over-sampling [C]//Workshop on learning from imbalanced datasets II. 2003, 11. |
| [21] | GANGANWAR V. An overview of classification algorithms for imbalanced datasets[J]. International Journal of Emerging Technology and Advanced Engineering, 2012, 2(4): 42-47. |
| [22] | PROVOST F. Analysis and visualization of classifier performance: comparison under imprecise class and cost distributions[C]// International Conference on knowledge Discovery & Data Mining. 1999: 43-48. |
| [23] | FAN X, TANG K. Enhanced maximum AUC linear classifier [C]// International Conference on Fuzzy Systems and Knowledge Discovery, Fskd 2010, 10-12 August 2010, Yantai, Shandong, China. 2010: 1540-1544. |
| [24] | KUBAT M, MATWIN S. Addressing the curse of imbalanced training sets: one-sided selection [C]// In Proceedings of the Fourteenth International Conference on Machine Learning. 2000: 179--186. |
| [25] | KAUFMAN L, ROUSSEEUW P J. Finding groups in data. an introduction to cluster analysis[J]. Wiley, 1990. |
 2017, Vol. 20
2017, Vol. 20