煤炭开采企业作为煤矿资源型地区的支柱产业，对地方经济发展和社会稳定发挥着举足轻重的作用。另一方面，由于煤炭开采自身的特殊性，开采工作大多在地下进行，矿井可深达地下几十米；同时，由于地质环境的错综复杂，受到的外部环境影响很多，导致安全生产中存在多种不确定因素，给人们生命财产安全带来极大威胁。以山西煤矿安全监察局于2016年5月5日发布的《全省煤矿安全生产统计分析》数据为例，一季度全省煤矿累计发生生产安全事故3起，死亡22人，同比死亡人数增加12人，上升120%。其中：国有重点煤矿事故2起，死亡21人，同比起数持平，死亡人数增加15人，上升250%；地方煤矿事故1起，死亡1人。因此，有效识别煤炭开采企业潜在风险，进而有效防范风险，降低事故发生率，将煤矿事故发生对人民生命财产安全造成的损失降为最低有着重大意义。

为了保障煤炭开采企业的安全生产，国家出台了一系列促进煤炭开采企业战略转型的政策，促进其快速转型。为了有效降低事故发生率，国家加大了对煤炭企业的安全生产管理力度，特别注重国有重点煤矿的安全生产，特别针对瓦斯爆炸和煤矿水害事故出台一系列政策。国家煤矿安全监察局也特别注重这几方面的监察和查处，并加大了对煤矿开采准许权的和生产许可的监管力度，严厉查处非法违法生产。但是，煤炭开采企业安全生产管理仍存在问题，煤矿事故仍时有发生。

煤炭开采企业本身的高风险性和极大的破坏性，使得如何科学管理风险成为煤炭行业发展过程中亟待解决的现实问题。而这一现实问题的有效解决，首先就需要从系统科学的视角，全面识别煤炭开采企业所面临的风险，以及企业生产系统中的薄弱环节和关键项目。因为识别风险是管理风险的前提与基础，也是指定改进控制措施的依据。已有的相关研究主要集中在以下几方面。①煤炭开采企业风险识别的视角，主要从安全生产风险、安全管理风险、外部风险和财务风险视角识别煤炭企业的风险^[1]；从矿区生态、煤矿环境以及煤矿排矸场环境的视角出发识别煤炭企业的风险源^{[2- 4]}；从煤炭企业个别高风险单元的视角出发对煤炭开采企业风险进行识别，如瓦斯爆炸风险识别^{[5- 7]}，巷道冒顶高风险区域识别^[8]；从实证研究的视角对大型国有煤炭企业的风险因素进行识别^[9]；也有从煤炭物流网络角度出发对煤炭企业进行分析并提出相应应对措施^[10]；此外也有文献通过建立风险指标体系对煤炭企业风险进行识别，如从人－机－环－管理4个方面建立风险预警指标体系^[11]以及从安全、质量、进度、成本风险因素4方面得到的立体模块化管理的风险指标体系^[12]。②煤炭开采企业风险识别的方法，主要有应用鱼骨图、决策树等方法追溯风险及其最根本的风险原因，也即知识型风险识别方法^[13]；根据价值链、平衡积分卡等方法对煤炭开采企业从绩效评估视角识别风险^{[14- 15]}；还有一些研究应用流程分析方法从任务层面分析对煤炭开采企业的运营风险进行识别^[16]，以及层次分析法^[17]、结构方程模型分析法^[18]等；此外，还有一些研究将计算机技术与信息化技术相结合对煤炭企业进行风险识别，并将识别出的各种危险因素建立安全风险信息系统或者风险信息数据库^{[19- 20]}。

由此可见，已有研究主要从经营，安全或个别风险角度对煤炭开采企业风险进行识别，鲜有从生产流程的角度对煤炭开采企业进行全面风险识别。此外，已有文献中运用FMEA方法对煤炭开采企业生产过程的风险进行全面识别的研究较少，且是运用传统FMEA简单的求和或乘积来求得风险优先度(RPN)^{[3, 19]}，存在一定的局限性^{[20- 22]}。

基于此，为了克服传统FMEA分析方法的弊端，本文将FMEA和模糊VIKOR方法用于煤炭开采企业的风险识别研究中，为煤炭开采企业风险识别提出一套系统、科学、客观的方法，使企业生产风险从源头上得以控制，最后再以某煤炭开采企业为例进行案例分析，使FMEA和模糊VIKOR方法的合理有效性得以验证。

1 识别过程 1.1 识别方法介绍

FMEA(failure modes and effect analysis)简称失效模式与影响分析，最初是由美国于上世纪50年代初提出，用于战斗机操作系统设计分析^{[20- 22]}。FMEA是一种前瞻性的可靠性分析和安全性评估方法，在预防事故的保护机制系统中被广泛应用。该方法通过分析系统中每一个潜在的故障模式，既可以有效进行风险识别，又可以确定其对系统所产生的影响，从而识别系统中的薄弱环节和关键项目，为指定改进控制措施提供依据，强调“事前预防”，而非“事后纠正”。

依据煤炭开采企业的生产流程将其划分为若干个生产单元，以此作为分析节点，对其进行FMEA分析。在具体分析过程中，从“人、机、料、法、环”5个方面着手，对每一个节点的潜在失效原因，潜在失效模式，潜在失效后果进行分析。将分析结果整理成故障失效模式分析表，根据现有的资料和产品生产过程，分析流程的结构，鉴别系统的每一个潜在的故障模式，分析引起故障的原因，建立一份完整的“故障模式分析表格”(表格形式参考 表2)，然后利用统计方法，估算故障发生时的发生频率( O)，严重度( S)，不易探测度( D)，并计算 O， S和 D的乘积得出风险优先度(RPN)。

VIKOR是一种折中的多属性群决策方法，最初由Opricovic提出。由于人的理解、判断、直觉和偏好等具有模糊、难于测量等特点，使得煤炭企业风险指标数据难以实测。因此，本文运用模糊VIKOR方法进行风险识别。具体是在得到“故障失效模式分析表”的基础上，从该表中整理出潜在风险，然后组织分析小组，按照以下步骤识别潜在风险。具体步骤如下。

1)明确决策者，评价标准和可行方案。假设有 n个决策者， y个评价标准， m个可行方案。

2)定义语言变量和其相对应的三角模糊数。语言变量用于评判评价标准的重要程度及相应等级(见 表1)。

假设模糊集 $\tilde A{\rm{ = }}\left( {{a_1}{\rm{,}}{a_2}{\rm{,}}{a_3}} \right)$ 为三角模糊数，三角模糊数 $\tilde A$ 对应的隶属度函数 $\mathop u\nolimits_{\tilde A} \left( x \right)$ 为

$\mathop u\nolimits_{\tilde A} \left( x \right){\rm{ = }}\left\{ {\begin{array}{*{20}{l}}{0{\rm{,}}}&{x {\text{＜}} a;}\\{\left( {x{\rm{ - }}a} \right)/\left( {b{\rm{ - }}a} \right){\rm{,}}}&{a {\text{≤}} x {\text{≤}} b;}\\{\left( {c{\rm{ - }}x} \right)/\left( {c{\rm{ - }}b} \right){\rm{,}}}&{b {\text{≤}} x {\text{≤}} c;}\\{0{\rm{,}}}&{x {\text{＞}} c{\text{。}}}\end{array}} \right.$

(1)

假设模糊集 $\tilde A{\rm{ = }}\left( {{a_1}{\rm{,}}{a_2}{\rm{,}}{a_3}} \right)$ ， $\tilde B{\rm{ = }}\left( {{b_1}{\rm{,}}{b_2}{\rm{,}}{b_3}} \right)$ ，且 ${a_1} {\text{≤}} {a_2} {\text{≤}} {a_3},{b_1} {\text{≤}} {b_2} {\text{≤}} {b_3}$ 。定义三角模糊数的基本运算法则如式(2)~(6)。运算后形成新的模糊集不一定按照由小到大的顺序排列参数。

$ \quad\quad {\text{加法规则}}:\tilde A + \tilde B{\rm{ = }}\left( {{a_1} + {b_1}{\rm{,}}{a_2} + {b_2}{\rm{,}}{a_3} + {b_3}} \right);$

(2)

$ \quad\quad {\text{减法规则}}:\tilde A{\rm{ - }}\tilde B{\rm{ = }}\left( {{a_1}{\rm{ - }}{b_3}{\rm{,}}{a_2}{\rm{ - }}{b_2}{\rm{,}}{a_3}{\rm{ - }}{b_1}} \right);$

(3)

$ \quad\quad {\text{乘法规则}}:\tilde A \times \tilde B{\rm{ = }}\left( {{a_1}{a_2}{\rm{,}}{b_1}{b_2}{\rm{,}}{a_3}{b_3}} \right);$

(4)

$\begin{split}& \quad\quad {\text{任意实数乘以一个模糊三角函数规则}}: \\& r \times \tilde A{\rm{ = }}\left( {r{a_1}{\rm{,}}r{a_2}{\rm{,}}r{a_3}} \right);\end{split}$

(5)

$ \quad\quad {\text{除法规则}}:\tilde A \div \tilde B{\rm{ = }}\left( {{a_1} \div {b_3}{\rm{,}}{a_2} \div {b_2}{\rm{,}}{a_3} \div {b_1}} \right)\text{。}$

(6)

其中， b ₁， b ₂， b ₃≠0。

3)计算综合的模糊方案排序。若有 n个决策者，则每一个可行方案的排序可由式(7)~(8)确定。

$ \quad\quad \tilde {{x_{i{\rm{,}}j}}}{\rm{ = }}\frac{{\sum\limits_{t{\rm{ = }}1}^n {{x^t}_{i{\rm{,}}j}} }}{n};$

(7)

$ \quad\quad \tilde {{W_j}}{\rm{ = }}\frac{{\sum\limits_{t{\rm{ = }}1}^y {w_j^t} }}{y}{\text{。}}$

(8)

4)计算模糊加权平均并构建模糊决策矩阵：

$\begin{split}& \quad\quad {B}{\rm{ = }}\left[ {\begin{array}{*{20}{c}}{{{\tilde x_{11}}}}&{{{\tilde x_{12}}}}&{{{\tilde x_{13}}}}& \vdots &{{{\tilde x_{1n}}}}\\{{{\tilde x_{21}}}}&{{{\tilde x_{22}}}}&{{{\tilde x_{23}}}}& \vdots &{{{\tilde x_{2n}}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\{{{\tilde x_{m1}}}}&{{{\tilde x_{m2}}}}&{{{\tilde x_{m3}}}}& \vdots &{{{\tilde x_{mn}}}}\end{array}} \right],\\[8pt]& \quad\quad {W} = \left( {{{\tilde W}_1},{{\tilde W}_2}, \cdots ,{{\tilde W}_n}} \right){\text{。}}\end{split}$

(9)

其中， $\tilde {{x_{i{\rm{,}}j}}}$ 是方案 ${\tilde A_i}$ 关于评价标准 Y _j 的评分， $\tilde {{W_j}}$ 为第 j个评价标准的重要程度，即权重。文中语言变量 ${{\tilde x_{i{\rm{,}}j}}}$ ， $\tilde {{W_j}}$ 均为三角模糊数。

5)确定模糊最优值( $\tilde {f_j^ * }$ )和模糊最劣值( $\tilde {f_j^{\rm{ - }}}$ )：

$\quad\quad \tilde {f_j^ * }{\rm{ = }}\mathop {\max }\limits_i {{\tilde x_{i{\rm{,}}j}}}{\rm{,}}\tilde {f_j^{\rm{ - }}}{\rm{ = }}\mathop {\min }\limits_i {{\tilde x_{i{\rm{,}}j}}}{\text{。}}$

(10)

6)计算最大群效应( $\tilde {{S_i}}$ )和最小个别遗憾值( $\tilde {{R_i}}$ )：

$ \quad\quad \tilde {{S_i}}{\rm{ = }}\sum\limits_{j{\rm{ = }}1}^y {\frac{{\tilde {{w_j}}\left( {\tilde {f_j^ * }{\rm{ - }}{{\tilde x_{ij}}}} \right)}}{{\tilde {f_j^ * }{\rm{ - }}\tilde {f_j^{\rm{ - }}}}}} ;$

(11)

$ \quad\quad\tilde {{R_i}}{\rm{ = }}\mathop {{\rm{max}}}\limits_j \left[ {\frac{{\tilde {{w_j}}\left( {\tilde {f_j^ * }{\rm{ - }}{{\tilde x_{ij}}}} \right)}}{{\tilde {f_j^ * }{\rm{ - }}\tilde {f_j^{\rm{ - }}}}}} \right]{\text{。}}$

(12)

其中， $\tilde {{w_j}}$ 是每一个评价标准的模糊权重。

7)计算综合评价值：

$ \quad\quad {{\tilde Q_i}}{\rm{ = }}v\left[ {\frac{{{{\tilde S_i}}{\rm{ - }}{{\tilde S^ * }}}}{{{{\tilde S^{\rm{ - }}}}{\rm{ - }}{{\tilde S^ * }}}}} \right] + \left( {1{\rm{ - }}v} \right)\left[ {\frac{{{{\tilde R_i}}{\rm{ - }}{{\tilde R^ * }}}}{{{{\tilde R^{\rm{ - }}}}{\rm{ - }}{{\tilde R^ * }}}}} \right]{\text{。}}$

(13)

其中， ${{\tilde S^ * }}{\rm{ = }}\mathop {\min }\limits_i \left\{ {{{\tilde S_i}}} \right\}{\rm{,}}{{\tilde S^{\rm{ - }}}}{\rm{ = }}\mathop {\max }\limits_i \left\{ {{{\tilde S_i}}} \right\},$ $\widetilde {{R^*}}{\rm{ = }}\mathop {\min }\limits_i \left\{ {\widetilde {{R_i}}} \right\},$ ${{\tilde R^{\rm{ - }}}{\rm{ = }}\mathop {\max }\limits_i \left\{ {\widetilde {R_i}} \right\}}{\text{。}}$

设 v为最大群效用权重。如果 v＞0.5，则说明大多数决策者偏好该方案；如果 v=0.5，则说明决策者的态度基本一致；如果 v＜0.5，则说明大多数决策者持否定态度，一般 v=0.5即折衷的态度。

8)去模糊化。根据以下公式对综合评价值进行去模糊化处理，并将结果按照从小到大的顺序排序。

$ \quad\quad T\left( {\tilde A} \right){\rm{ = }}\frac{{\alpha + 2\beta + \gamma }}{4}{\text{。}}$

(14)

9)如果满足以下条件，则认为方案 A _i 得到了最佳排序。

①有 $Q\left( {{A^{\left( 2 \right)}}} \right){\rm{ - }}Q\left( {{A^{\left( 1 \right)}}} \right) {\text{≥}} BQ$ 且 $Q:BQ{\rm{ = }}\displaystyle\frac{1}{{m{\rm{ - }}1}}$ 。

②只有当按照 S _i 和 R _i 排序方案 A ⁽¹⁾均为最佳排序时，所得到的这种折衷解才具有稳定性。

若上述2个条件只符合其一则折衷解就会有所不同，具体而言：若只满足条件(1)则最优折衷解为 A ⁽¹⁾和 A ⁽²⁾；若只满足条件(2)，则最优折衷解为 A ⁽¹⁾， A ⁽²⁾，…， A ^{( M)} ，且 $Q\left( {{A^{\left( M \right)}}} \right){\rm{ - }}Q\left( {{A^{\left( 1 \right)}}} \right) {\text{＜}} BQ$ 。

1.2 风险识别过程

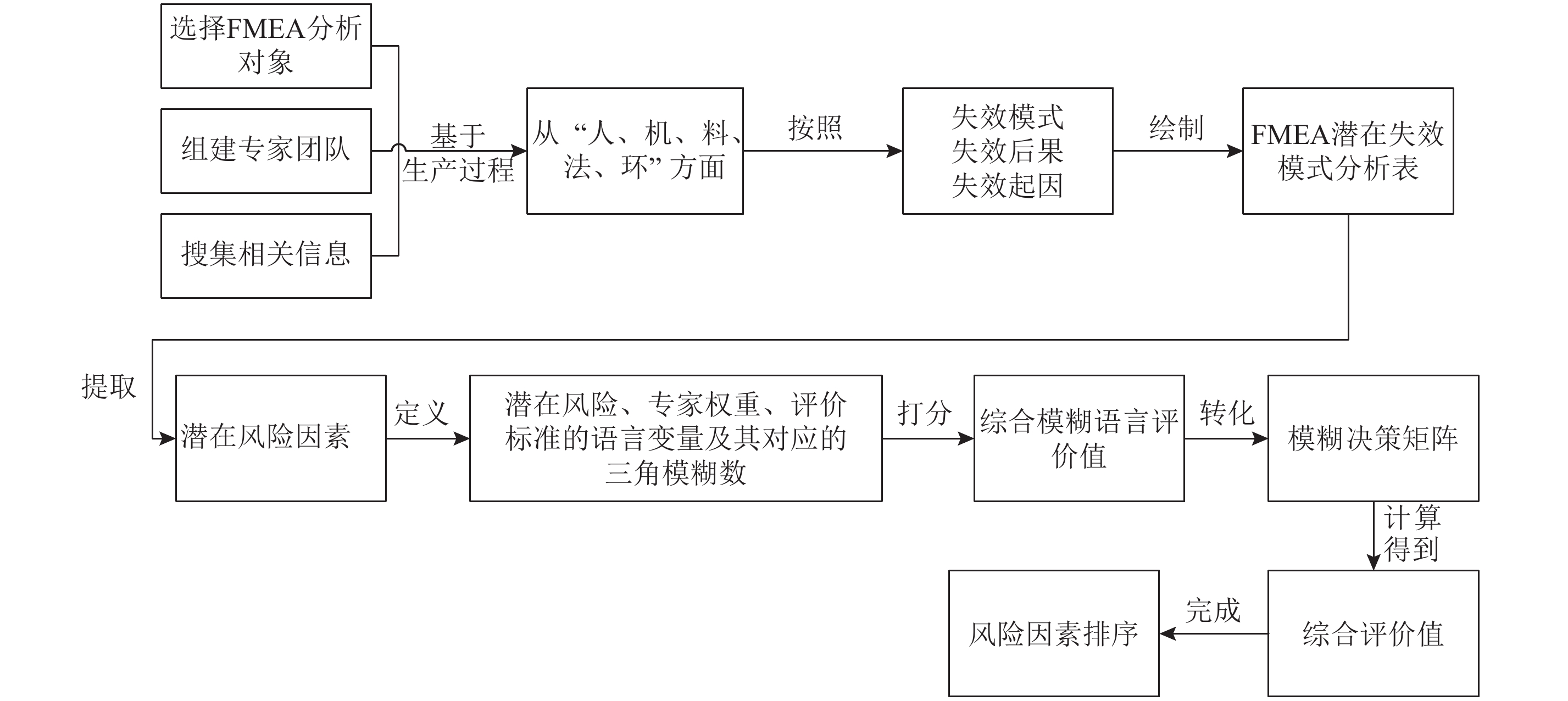
将FMEA和模糊VIKOR方法进行科学结合，既运用了FMEA的思想，又采用了模糊VIKOR的算法，从而保证了风险识别的客观性和精确度，具体的风险识别过程见 图1所示。

2 案例分析 2.1 案例概况

本案例以某煤炭开采企业为例。该企业成立于1980年9月，是一个特大型传统煤炭开采企业，井田面积13.25 km ²，年设计生产能力已突破500万t，该企业煤炭开采为主平硐、斜井开拓，采煤方法采用综合机械化生产。该煤矿企业井下设备种类众多，由于设备设施故障导致的事故屡有发生。

2.2 案例企业风险识别过程

1)各生产单元的FMEA潜在失效模式分析。

为了对该企业进行FMEA分析，根据煤炭开采企业的生产流程，将企业分为9个功能模块，也就是9个生产单元。本研究邀请该企业生产单元的负责人、技术负责人以及企业安全生产负责人等3位企业成员和2位高校长期从事应急管理研究的学者组成专家团队，最终确定了各个生产单元的在用设备，并收集了相关资料，进行FMEA潜在失效模式分析(见 表2)。

2)由 表2整理出该企业的潜在风险(见 表3)。

3)潜在风险的语言变量及其对应的三角模糊数(见 表1)。参考文献[23]各位专家的知识背景和经历都不同，所以各位专家所给的意见也应赋以不同的权重(见 表4)。根据FMEA方法的原理，由于3个评价标准 O， S， D具有相同的重要程度，因此文章在此赋予3个评价标准相同的权重(见 表5)。

4)5位专家以3个评价标准为依据对所有潜在风险进行打分得到综合模糊语言评价值(见 表6)。

5)根据 表1和 表4的语言变量，将 表6转化为模糊决策矩阵(见 表7)。

6)根据公式(10)可计算得到评价标准的模糊最优值( $\tilde {f_j^ * }$ )和模糊最劣值( $\tilde {f_j^{\rm{ - }}}$ )(见 表8)。

7)根据公式(11)、(12)计算得到计算最大群效应( $\tilde {{S_i}}$ )和最小个别遗憾值( $\tilde {{R_i}}$ )，取 v=0.5，根据公式(13)计算综合评价值 $\tilde {{Q_i}}$ (见 表9)。

8)去模糊化。根据公式(14)对综合评价值 $\tilde {{Q_i}}$ 进行去模糊化处理，并按照从小到大的顺序排序，结果见 表10。

3 结语

本文针对传统FMEA在计算RPN时不够精准、主观性较强的不足，将模糊VIKOR方法引入到煤炭开采企业潜在风险因素的最终评价中，以某煤炭开采企业为例从9个生产单元，5个方面对企业进行了FMEA潜在失效模式分析，提取出了20个潜在风险因素。在此基础上，应用模糊VIKOR的方法不仅识别出潜在风险的关键风险，还得到每一个潜在风险的排序。在具体评价时还考虑了由于专家知识背景及经验不同而赋予专家不同权重，同时遵循考虑最大群效应和最小个别遗憾值的折衷思想对各潜在风险进行排序。研究结果明确了该企业的主要潜在风险，表明了FMEA和模糊VIKOR方法的科学结合能够克服传统FMEA的局限性，有效识别煤炭企业的主要潜在风险，而且识别结果可以为企业制定突发事件应急预案或应急管理机制提供参考。