近年来主题工业区和主题经济开发区在我国各省、市、地区蓬勃发展,形成了区域内或相邻区域间的多供应商、多制造商( n- n)组成的物流系统网络。与传统物流系统(1-1、1- n、 n-1)不同,该类物流系统复杂,合理规划运输路径困难。通过智能优化技术,合理规划 n- n物流系统的运输方案,不仅能加强供应商与制造商之间的合作、降低整个物流系统的成本,也能减少对社会流通的影响和压力。
针对不同运输策略,入厂物流模式主要分为直送、越库及循环取货3种模式。直送作为企业最早使用与最基本的入厂物流运输模式,具有简单快捷等优点。马东彦[1]研究了基于直送的两阶段混合调度模型。但该文献着重对算法的研究,对直送模式运作的分析不够细致。邱晗光[2]研究了第三方物流直送配货的运作模式,并将该模式与其他模式对比分析,明确了不同模式的实施情形。越库是在配送中心内建立临时库存,对货品进行卸载、分拣、装载出库并运送至客户手中的内部转移形式。文献[3- 8]均建立了越库运输的车辆路径规划模型,并设计启发式算法进行求解。循环取货是指同一货运车辆对多个供应商或需求点进行循环取货的运作模式,适用于多站点( n-1)小批量近距离运输。文献[9- 14]均对循环取货模式进行深入研究,并设计算法进行有效求解。Toshinori等[15]通过案例分析的方式,对3种运输模式进行了对比分析,阐述了3种运输模式的优势及适用范围。
综上,虽然3种模式已得到深入研究,但仍缺少综合3种模式进行园区运输方案设计的研究。国内外已有对 n-1运输规划问题的研究,但缺乏 n- n入厂物流系统的广泛探讨。另外,即使Oded等[4]对 n- n物流系统进行研究,但仅限于越库与直送模式的车辆路径问题研究,缺乏对3种运输模式的综合考虑,难以形成更加合理的运输方案。本文综合考虑直送、越库及循环取货3种模式的特征和优势,将3种模式延拓到 n- n入厂物流系统的研究空间下,以最小化运输成本为目标,建立非线性规划模型,并给出运输模式与路径的设计方法,对 n- n物流系统的运输方案进行规划研究。
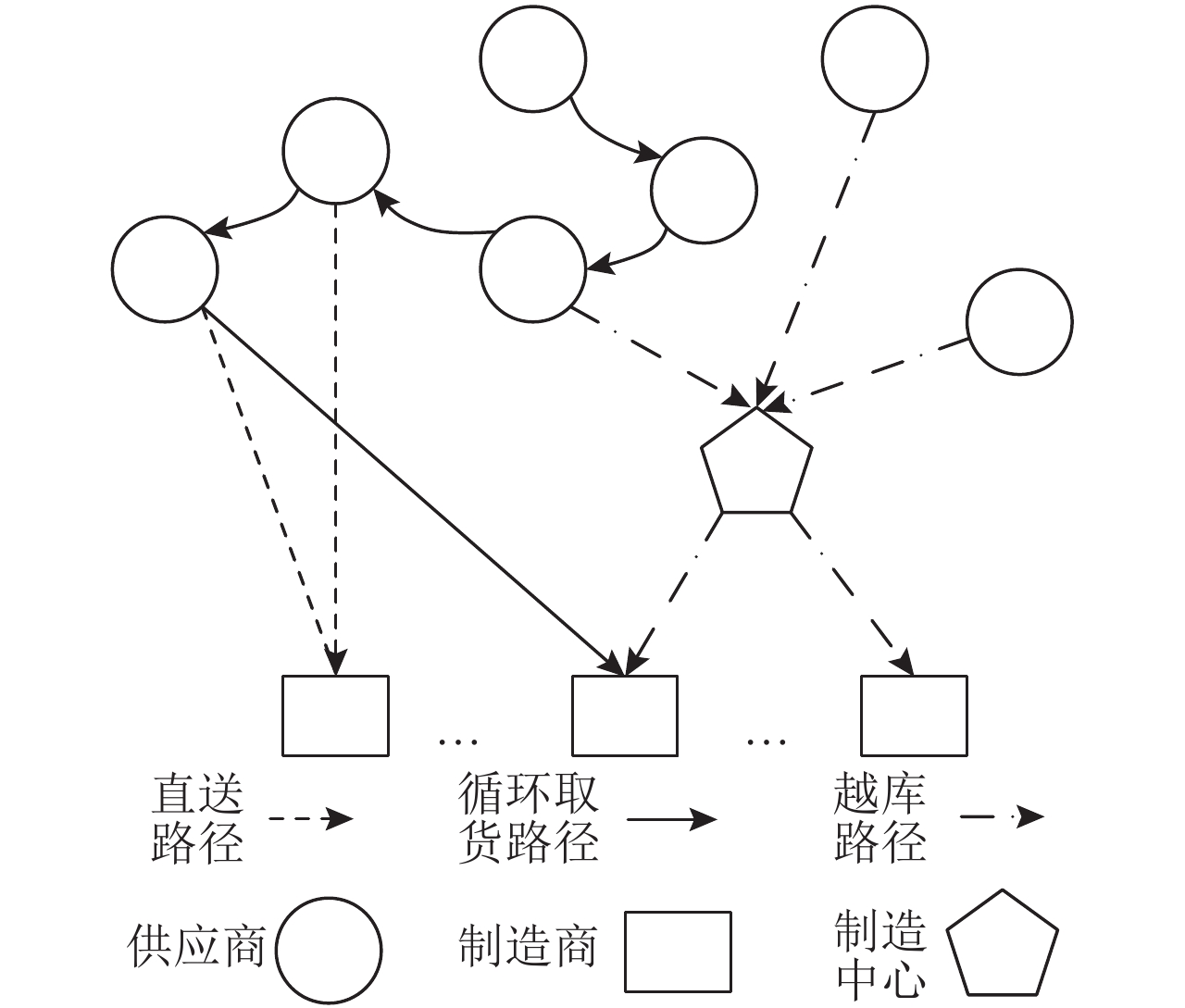
1 入厂物流运输方案的规划问题 1.1 问题描述如 图1所示,某相关区域内若干家供应商,通过直送、循环取货、越库3种方式向相邻区域的若干家制造商供应若干类零部件。本文针对此类 n- n物流系统情境,以系统总运输成本最低为目标,设计合理的运输模式与路径的规划方案。
|
图 1 基于3种运输模式的运输方案示意图 Fig. 1 Three kinds of transportation modes |
定义供应商点集 V={1, 2,…, n},制造商点集 W={1, 2,…, m}, i, j∈ V, k∈ W, l k ( l k =1, 2,…, m k )表示制造商 k用于循环取货的车辆编号;制造商 k用于循环取货的编号为 l k 的汽车在供应商 g l k 处发车,经过循环取货后,到达最后一个供应商 h l k 处取货,最后运回至制造商 k,在模型中以约束的方式加以说明;定义决策变量如下。
| ${y_{i{l_k}}} = \!\! \left\{ {\begin{array}{*{20}{l}}\!\!\!\! {1,} {{\text{制造商}}k \text{用于循环取货的车辆}{l_k}\text{去供应商}i\text{处取货}};\\\!\!\!\! {0,} \text{否则}{\text{。}}\end{array}} \right.$ |
| ${x_{ij{l_k}}} \!\!= \!\! \left\{ {\begin{array}{*{20}{l}}\!\!\!\! {0,} {\text{制造商}k\text{用于循环取货的车辆}{l_k}\text{从供应商}i\text{运输至}j};\\\!\!\!\! {1,} \text{否则}。\end{array}} \right.$ |
| $\begin{split}\\[-2pt]{{\rm{min}}Z = \displaystyle\sum\limits_{k \in W} {\sum\limits_{{l_k} = 1}^{{m_k}} {\sum\limits_{i \in V} {\sum\limits_{j \in V} {{C_{ij}}{x_{ij{l_k}}}} } } } + \sum\limits_{k \in W} {\sum\limits_{{l_k} = 1}^{{m_k}} {{C_{{h_{{l_k}}}k}}} } + }\\\sum\limits_{i \in V} {{C_{i0}}\left[ {\sum\limits_{k \in W} {{D_{ki}}\left( {1 - \sum\limits_{{l_k} = 1}^{{m_k}} {{y_{i{l_k}}}} } \right)} /Q - \varepsilon + 1} \right]} + \\\sum\limits_{k \in W} {{C_{0k}}\left[ {\sum\limits_{i \in V} {{D_{ki}}\left( {1 - \sum\limits_{{l_k} = 1}^{{m_k}} {{y_{i{l_k}}}} } \right)} /Q - \varepsilon + 1} \right]\text{。}} \end{split}$ | (1) |
s.t.
| $\begin{array}{*{20}{c}}\quad\quad {{m_k} = \left[ {\displaystyle\sum\limits_{{l_k} = 1}^{{m_k}} {\sum\limits_{i \in V} {{D_{ki}}{y_{i{l_k}}}/(aQ)} } } \right] + 1,}&{k \in W};\end{array}$ | (2) |
| $\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}\quad\quad {\displaystyle\sum\limits_{i \in V} {{D_{ki}}{y_{i{l_k}}}} {\text{≤}} Q,}&{k \in W;}\end{array}}&{{l_k} = 1,2, \cdots ,{m_k}};\end{array}$ | (3) |
| $\begin{array}{*{20}{c}}\quad\quad {\displaystyle\sum\limits_{{l_k} = 1}^{{m_k}} {{y_{i{l_k}}}} = 0{\text{或}}{\rm{1,}}}&{i \in V;}&{k \in W};\end{array}$ | (4) |
| $\begin{array}{*{20}{c}}\quad\quad {\displaystyle\sum\limits_{i \in V} {{x_{i{g_{{l_k}}}{l_k}}}} = 0,}&{{l_k} = 1,2, \cdots ,{m_k};}&{k \in W};\end{array}$ | (5) |
| $\begin{array}{*{20}{c}}\quad\quad {{y_{{g_{{l_k}}}{l_k}}} = 1,}&{{l_k} = 1,2, \cdots ,{m_k};}&{k \in W};\end{array}$ | (6) |
| $\begin{array}{*{20}{c}}\quad\quad {\displaystyle\sum\limits_{j \in V} {{x_{{h_{{l_k}}}j{l_k}}}} = 0,}&{{l_k} = 1,2, \cdots ,{m_k};}&{k \in W};\end{array}$ | (7) |
| $\begin{array}{*{20}{c}}\quad\quad {{y_{{h_{{l_k}}}{l_k}}} = 1,}&{{l_k} = 1,2, \cdots ,{m_k};}&{k \in W};\end{array}$ | (8) |
| $\quad\quad$\begin{split}\\[-2pt]\quad\quad \sum\limits_{i \in V} {{x_{ij{l_k}}}} = {y_{j{l_k}}},j \in V,j \ne {g_{{l_k}}}, {l_k} = 1,2, \cdots ,{m_k}k \in W;\end{split}$$ | (9) |
| $\begin{split}\\[-2pt]\quad\quad \sum\limits_{j \in V} {{x_{ij{l_k}}}} = {y_{i{l_k}}},i \in V,i \ne {h_{{l_k}}}, {l_k} = 1,2, \cdots ,{m_k},k \in W;\end{split}$ | (10) |
| $\begin{array}{*{20}{c}}\quad\quad{{x_{j{l_k}}} = 0{\text{或}}1,} {i、j \in V,} {{l_k} = 1,2, \cdots ,{m_k},} {k \in W};\end{array}$ | (11) |
| $\begin{array}{*{20}{c}}\quad\quad {{y_{i{l_k}}} = 0{\text{或}}1,} {i、j \in V,} {{l_k} = 1,2, \cdots ,{m_k},} {k \in W}\text{。}\end{array}$ | (12) |
目标函数(1)式中表示循环取货方式中供应商与供应商之间的运输、循环取货方式从供应商运输至制造商、越库模式从供应商运输至配送中心以及从配送中心运输至制造商的总费用。其中, C ij 为供应商 i与供应商 j之间的运输费用, C ik 为供应商 i到制造商 k的运输费用, C i0 为供应商 i运输至越库的运输费用, C 0 k 为从越库运输至制造商 k的运输费用,模型中所有的“[]”表示对内部取整。
1.3 算法设计该问题是NP难问题,本文设计了基于一种新编码方式的模拟退火算法计算该数学模型,并用Matlab软件编程实现。模拟退火算法已在理论上被证明是一种以概率1收敛于全局最优解的全局优化算法[7]。
1.3.1 解的编码方法该问题解的编码可用一个 m× n的矩阵表示,其中, m表示制造商的数量, n表示供应商数量。 x ij 表示矩阵的的第 i行第 j列的数。若 x ij =0,则表示制造商 i对供应商 j的零部件需求量通过越库方式运输,若 x ij ≠0,则表示制造商 i对供应商 j的零部件需求量通过循环取货方式运输,且表示供应商 j的排列顺序为 x ij 。再考虑到每辆车的最大装载量,可以依次将各个供应商划入各辆车的循环取货路径中,确定循环取货的路径。
1.3.2 基于3种变异操作的邻域选择方法解的邻域选择主要有3种变异操作:由越库转变为循环取货,由循环取货转变成越库,循环取货方式中改变供应商排列顺序进行两两交换。具体邻域选择操作如下。
步骤1 确定3种变异操作的概率: P 1、 P 2、 P 3。
步骤2 对于矩阵的第 i行,记该行中最大的数为max,当该行中不存在“0”或者 P 1<rand()(区间[0, 1]的均匀分布中随机产生的一个数)时,转步骤4;否则选择其中任意一个“0”,将其变为[1, max]区间内的任意一个数整 r。
步骤3 将该行中大于等于 r的数都加上1(2个 r保留第1个)。
步骤4 当该行中的数全为零,或者 P 2<rand()时,转步骤6;否则随机选择其中一个非零的数 q,将其变为“0”。
步骤5 将该行中大于 q的数都减去1。
步骤6 当该行中非零的数少于2个,或者 P 3<rand()时,转至步骤7;否则随机选择2个非零的数进行交换。
步骤7 i= i+1,转步骤2。
1.3.3 模拟退火算法实现本文基于文献[16]中提出的模拟退火算法求解该问题,并采用简单直观的降温方法 t k+1 = a· t k ,温度迭代步长为 N;终止准则采用温度下降至0.1停止计算,具体步骤如下。
步骤1 产生一个初始可行解 X 0,令当前解等于 X 0,最优解等于 X 0,最优解的评价值等于当前解的评价值,当前迭代步数 k=0,当前温度 t k = t max。
步骤2 若在该温度内达到内循环停止条件(迭代次数达到固定步长 N),则转步骤4;否则,进行邻域选择操作,得到一个邻域解并计算该邻域解的评价值。
步骤3 计算得到的邻域解与原来解评价值的差 Δ,若 Δ≤0,则使该解成为当前解,否则,以exp(- Δ/ t k )的概率成为当前解,并比较当前解的评价值与最优解的评价值,若当前解的评价值小于最优解的评价值,则将当前解赋给最优解,当前解的评价值赋给最优解,重复第2步。
步骤4 k= k+1, t k = a· t k ,若满足 t k <0.1,转第5步;否则转第2步。
步骤5 算法终止并输出结果。
2 算例及结果本文通过运行6个算例证明算法的有效性,在CPU 2.27 GHz,内存4G的计算机平台上利用Matlab2008a完成对上述模拟退火算法(SA)与禁忌搜索算法(TS)的实现,其中禁忌搜索在文中作为参照,评价方法、邻域选择及目标函数评价值与模拟退火算法相同,且具体实现方法参照文献[17]。每个算例运行10次,得到结果如 表1所示。
| 表 1 模拟退火算法(SA)与禁忌搜索算法(TS)运行结果对比 1) Tab. 1 Result comparison between SA and TS |
计算结果显示,模拟退火算法(SA)与禁忌搜索算法(TS)求解问题所需的计算时间基本相同,但SA得到的计算结果优于TS:1)SA求得费用最小值及费用均值均小于(个别等于)TS;2)SA求得费用值标准差小于TS,表明SA具有更好的稳定性。
2.1 算例结果解释与分析具体解释以算例6为例,假设运输路线均为直线运输,运输费用与运输距离成正比,本文设定其比例为1:1;设定一辆车的最大容载量为100(%)。具体数据,制造商以及供应商的地址坐标以及运输量,如 表2。
| 表 2 制造商、供应商的坐标及需求量 Tab. 2 The location and demand of manufacturers and suppliers |
调试后确定算法初始温度5 000,迭代步长2 000,降温系数 a=0.96,3种邻域变异的选择概率分别为0.1、0.05、0.1,利用Matlab运行10次后,选取评价值(系统总费用)最低的解,其编码为:(4, 0, 6, 0, 0, 1, 0, 5, 0, 0, 3, 2);(3, 0, 4, 0, 1, 5, 0, 6, 0, 2, 0, 0);(4, 0, 3, 0, 0, 2, 0, 5, 0, 0, 0, 1);(3, 0, 4, 0, 1, 6, 0, 5, 0, 2, 0, 0);(4, 0, 6, 0, 3, 2, 0, 5, 0, 0, 0, 1);(2, 0, 4, 0, 0, 5, 0, 1, 0, 3, 0, 0)。循环取货的具体安排如 表3所示。
| 表 3 循环取货及直送的路径、车辆数、装载率、费用 Tab. 3 The route, car number, loading rate and expense of Milk-run and Direct transportation modes |
由 表3可知,采取循环取货或直送的运输费用为914.9,需要运输车辆为16辆,车辆的平均装载率为78.6%。其余零部件由越库模式运输,易得越库模式的运输费用为2 341.4,运输车辆25辆,平均装载率90.8%。因此算例6的总运输费用为3 256.3,总运输车辆为41辆,总平均装载率为86%。对于远距离运输的供应商7、9、11均采用越库模式(由于制造商1对供应商11的需求量相对于其他制造商大很多,接近运输车辆满载,因此采用直送模式);对于中距离运输的供应商2、4、5,除了供应商5的部分零部件采用循环取货之外,其余也都采用了越库运输;剩余近距离运输的供应商大部分选择循环取货或直送模式。由此可知,求解得到了运输总费用低、平均装载率高的更合理的综合运输方案。并验证了3种运输模式的优势及适用情境,即直送适用于大量运输,循环取货适用于近距离小批量运输,越库适用于远距离运输。
2.2 算例结果与其他方案对比本文结果通过与全部使用越库方式、全部使用循环取货方式、全部使用直送方式3种运输方案进行对比,体现该方法求解运输方案的优势,具体对比如 表4。
| 表 4 各运输方案对比 Tab. 4 The comparison among different transportation modes |
通过该方法求得的运输方案中,运输车辆为41辆,多于全部循环取货方案的28辆,但明显少于全部越库方案的56辆与全部直送方案的72辆。且求解的运输方案的运输费用远低于其他3种运输方案(分别低27.2%、31.4%、44.7%),车辆的平均装载率也在4种模式中最高。因此,该方法可求得车辆需求少、满载率高的更优的运输方案,降低系统总运输费用。
3 总结与展望本文研究了工厂集聚区 n- n入厂物流系统运输方案的规划问题,建立了非线性规划模型,并利用改进的模拟退火算法求解。算例验证了该方法的有效性并得到结论:对 n- n入厂物流运输方案进行合理规划可以有效提高车辆的满载率,减少运输车辆数并有效降低运输费用。研究结果为未来工业开发区、工厂集聚区的整体物流规划提供理论指导与技术支持。但本文在某些方面还存在欠缺,因此未来研究工作中会以下几个方面深入探索并不断完善:1)考虑越库模式下货物仓储时间对运输方案规划的影响;2)考虑各供应商取货时间窗的约束对运输方案规划的影响;3)考虑循环取货型越库以及制造商处的循环送货;4)考虑空车返回调度策略对运输方案规划的影响。
| [1] |
马东彦. 基于直送的两阶段混合调度模型的模拟退火算法研究[J].
物流技术, 2009, 28(10): 48-50.
MA Dongyan. Simulated annealing algorithm of two-stage hybrid scheduling model based on through transport[J]. Logistics Technology, 2009, 28(10): 48-50. DOI: 10.3969/j.issn.1005-152X.2009.10.016. |
| [2] |
邱晗光. 供应链协同供应配送策略研究[J].
物流技术, 2013, 32(11): 336-338.
QIU Hanguang. Study on supply chain joint supply and distribution strategy[J]. Logistics Technology, 2013, 32(11): 336-338. DOI: 10.3969/j.issn.1005-152X.2013.11.107. |
| [3] | LEE Y H, JUNG W J, LEE K M. Vehicle routing scheduling for cross-docking in the supply chain[J]. Computers & Industrial Engineering, 2006, 51(2): 247-256. |
| [4] | BERMAN Oded, QIAN Wang. Inbound logistic planning: minimizing transportation and inventory cost[J]. Transportation Science, 2006, 40(3): 287-299. DOI: 10.1287/trsc.1050.0130. |
| [5] | LIAO Ching-Jong, LIN Yaoming, SHIH S C. Vehicle routing with cross-docking in the supply chain[J]. Expert Systems with Applications, 2010, 37(10): 6868-6873. DOI: 10.1016/j.eswa.2010.03.035. |
| [6] |
麦家骥, 陈峰. 基于循环取料的不确定越库调度模型与算法[J].
上海交通大学学报, 2011, 45(2): 159-163.
MAI Jiaji, CHEN Feng. Uncertain milk run-based cross docking scheduling: model and algorithms[J]. Journal of Shanghai Jiaotong University, 2011, 45(2): 159-163. |
| [7] | MIAO Zhaowei, YANG Feng, FU Ke. Transshipment service through crossdocks with both soft and hard time windows[J]. Annals of operations research, 2012, 192(1): 21-47. DOI: 10.1007/s10479-010-0780-4. |
| [8] | DONDO R, CERDÁ J. A monolithic approach to vehicle routing and operations scheduling of a cross-dock system with multiple dock doors[J]. Computers & Chemical Engineering, 2014, 63: 184-205. |
| [9] | SADJADI S J, JAFARI M, AMINI T. A new mathematical modeling and a genetic algorithm search for milk run problem (an auto industry supply chain case study)[J]. The International Journal of Advanced Manufacturing Technology, 2009, 44(1-2): 194-200. DOI: 10.1007/s00170-008-1648-5. |
| [10] |
汪金莲, 蒋祖华. 汽车制造厂零部件入厂物流的循环取货路径规划[J].
上海交通大学学报, 2009, 43(11): 1703-1708.
WANG Jinlian, JIANG Zuhua. Routing for the Milk-Run Pickup System in Automobile Parts Supply[J]. Journal of Shanghai Jiaotong University, 2009, 43(11): 1703-1708. DOI: 10.3321/j.issn:1006-2467.2009.11.006. |
| [11] | GURINDER Singh Brar, GAGAN Saini. Milk run logistics: literature review and directions [C]//Proceedings of the World Congress on Engineering. 2011, 1: 6-8. |
| [12] | JAFARI-ESKANDARI M, ALIAHMADi A R, KHALEGHI G H H. A robust optimization approach for the milk run problem with time windows with inventory uncertainty: an auto industry supply chain case study[J]. International Journal of Rapid Manufacturing, 2010, 1(3): 334-347. DOI: 10.1504/IJRAPIDM.2010.034254. |
| [13] |
章勋宏, 贾国柱, 孔继利. 考虑零件三维装载约束带时间窗的循环取货路径问题研究[J].
管理工程学报, 2014, 28(4): 207-218.
ZHANG Xunhong, JIA Guozhu, KONG Jili. Vehicle routing problem with time windows under three-dimensional loading constraint based on milk-run[J]. Journal of Industrial Engineering /Engineering Management, 2014, 28(4): 207-218. |
| [14] |
朱伟军, 屈挺, 王宗忠, 等. 工业园区集配中心循环取货路径规划[J].
现代制造工程, 2015(9): 13-19.
ZHU Weijun, QU Ting, WANG Zongzhong. Milk run route planning for supply hub in industrial park[J]. Modern Manufacturing Engineering, 2015(9): 13-19. |
| [15] | TOSHINORI Nemoto, KATSUHIKO Hayashi, MASATAKA Hashimoto. Milk-run logistics by Japanese automobile manufacturers in Thailand[J]. Procedia-Social and Behavioral Sciences, 2010, 2(3): 5980-5989. DOI: 10.1016/j.sbspro.2010.04.012. |
| [16] |
邓爱民, 毛超, 周彦霆. 带软时间窗的集配货一体化VRP改进模拟退火算法优化研究[J].
系统工程理论与实践, 2009, 29(5): 186-192.
DENG Aimin, MAO Chao, ZHOU Yanting. Optimizing research of an improved simulated annealing algorithm to soft time windows vehicle routing problem with pick-up and delivery[J]. Systems Engineering——Theory & Practice, 2009, 29(5): 186-192. DOI: 10.12011/1000-6788(2009)5-186. |
| [17] | 郎茂祥. 配送车辆优化调度模型与算法[M]. 北京: 电子工业出版社, 2009. |
 2017, Vol. 20
2017, Vol. 20