热处理是机械零件加工过程一道重要工序。热处理不仅可以提高工件切削性能，而且对提高工件精度、强度和使用寿命有重要作用。工件每次热处理需要较长的加工时间，工件一般需要在热处理炉中加热保温几小时到几十小时，而且热处理炉功率较大，普通容量的热处理炉功率高达到几十千瓦以上，合理安排热处理工件的生产将对降低能耗和降低生产成本具有重大意义。在工件到达时间、质量、尺寸和交货期存在多种差异的情况下，如何充分利用热处理设备对工件进行有效调度，是热处理车间急需解决的一个难题。

热处理生产调度是近年来国内外的研究热点，文献[1- 6]在简化的模型下研究了热处理批调度算法。其中文献[1- 4]假定各批次的加工时间是定值，与批中装载量和工件尺寸无关。文献[5- 6]则假定各批次的加工时间由批中最大质量的工件决定。然而，文献[7]认为真空热处理各批次的加工时间取决于装炉量和批中有效厚度最大的工件。因此，在确定各批次加工时间时，必须同时考虑装炉量和批中最大工件尺寸，得到的调度模型和算法才比较符合热处理车间的实际应用。

热处理生产调度可以归类为批调度问题。根据各批次加工时间与批中工件的关系，批调度问题可分成3类。第1类假定各批次加工时间是定值，文献[3- 4]属于第1类，这2篇文献分别构造了以最小化最大完成时间为目标的混合整数线性规划(MILP)数学模型，并提出算法改进数学模型的计算效率。第2类假定各批次加工时间取决于批中最大工件，文献[8- 10]属于第2类。其中文献[8- 9]以单机和两机流水车间为调度环境分别提出了MILP数学模型，文献[10]提出领域搜索算法求解最小化最大拖期量为目标的单批处理机调度问题。第3类则假定各批次的加工时间为批中工件的加工时间之和，文献[11- 13]属于这一类型。其中文献[11]构建了以最小化最大拖期量为目标的单批处理机数学模型，文献[12]构建了以最小化最大完成时间为目标的混合整数规划数学模型，文献[13]研究了考虑机器故障和工件动态到达的批调度问题。文献[14]提出了两阶段流水车间批调度算法，其中前阶段属于第3类批调度问题，后阶段属于第1类调度问题。

本文研究的批调度问题是第2类和第3类的结合，各批次的加工时间受到总装载量和批中最大工件尺寸的双重约束。对现有国内外论文研究发现，尚无文献报道该类型批调度问题的相关研究。基于最小化最大完成时间和最小化最大拖期量是生产中最基本的两个调度目标，下文将分别构建MILP数学模型并提出满足企业应用需求的启发式算法。

1 问题描述

有 n个待加工工件需要经过真空热处理加工，工件的到达时间 r _j 、交货期 d _j 、质量 g _j 和尺寸 s _j 存在差异。车间现有一台热处理炉，热处理炉可以容纳多个工件同时加工，每一批次装载的工件总质量不能超过热处理炉的容量 G _max。各批次的加工时间受到该批次的总质量和批中工件最大尺寸的双重约束。文献[7]提出热处理过程中两次预热时间和最终保温时间的计算公式均为： T(min)=0.4 G+ D，即各批次的总加工时间为 T(min)=1.2 G+3 D，其中 G表示装炉量(kg)， D表示批中最大工件尺寸(mm)。对多间热处理企业调研发现，不同企业在计算各批次加工时间时应用的公式略有区别。为了使本文提出的数学模型和算法更具通用性，本文将各批次加工时间的计算公式总结为

$\quad\quad T = \alpha + \beta G + \gamma D{\text{。}}$

(1)

式(1)中固定时间 α以及权重系数 β和 γ的值可由各企业实际情况进行设定。各批次一旦在热处理炉上开始加工，不允许中途停下来或者插入其他批次。调度目标分别为最小化最大完成时间 C _max和最小化最大拖期量 L _max。采用调度问题的通用表示方法，求解最小化最大完成时间的调度问题可描述为 $\left. 1 \right|\left. {{\rm{batch}},\mathop r\nolimits_j ,\mathop g\nolimits_j ,\mathop s\nolimits_j } \right|\mathop C\nolimits_{\max } $ ，求解最小化最大完成时间的调度问题可描述为 $\left. 1 \right|\left. {{\rm{batch}},\mathop r\nolimits_j ,\mathop d\nolimits_j ,\mathop g\nolimits_j ,\mathop s\nolimits_j } \right|\mathop L\nolimits_{\max } $ 。下文使用到的集合、参数和变量定义如下。

集合：

J为工件集 { j∈ J}, J = {1, 2, …, n}， n表示工件总数量；

B为批次集 { b∈ B}, B = {1, 2, …, v}， v表示分批数量上界。

参数：

r _j 为第 j个工件的到达时间；

d _j 为第 j个工件的交货期；

g _j 为第 j个工件的质量；

s _j 为第 j个工件的尺寸；

G _max为设备的容量；

M为数值较大的整数；

α为固定加工时间；

β为装载量权重系数；

γ为工件尺寸权重系数。

决策变量：

${X_{jb}}\left\{ {\begin{array}{*{20}{c}}{ {\rm{1}},{\text{第}}j{\text{个工件被安排在第}}b{\text{个批次中;}}}\\[5pt]{ \!\!\!\! 0,{\text{否则}}{\text{。}}} \qquad \qquad \qquad \qquad \qquad\,\,\,\,\, \,\,\,\end{array}} \right.$

因变量：

S _b 为第 b个批次的开始加工时间；

P _b 为第 b个批次的加工时间；

C _j 为第 j个工件的完成时间；

C _max为最大完成时间；

L _max为最大拖期量。

2 最小化最大完成时间 2.1 混合整数线性规划数学模型(Model C)

$\quad\quad {\rm{min }}\mathop C\nolimits_{{\rm{max}}} {\text{。}}$

(2)

s.t.

$\quad\quad \sum\limits_{b \in B} {\mathop X\nolimits_{jb} } = 1,\;\forall j \in J;$

(3)

$\quad\quad \sum\limits_{j \in J} {\mathop g\nolimits_j } \mathop X\nolimits_{jb} {\text{≤}} \mathop G\nolimits_{\max } ,\forall b \in B;$

(4)

$ \quad\quad \mathop P\nolimits_b {\text{≥}} \alpha + \beta \sum\limits_{j \in J} {\mathop g\nolimits_j } \mathop X\nolimits_{jb} + \gamma \mathop s\nolimits_j \mathop X\nolimits_{jb} ,\;\forall b \in B,j \in J;$

(5)

$ \quad\quad \mathop S\nolimits_b {\text{≥}} \mathop r\nolimits_j \mathop X\nolimits_{jb} ,\forall b \in B,j \in J;$

(6)

$ \quad\quad \mathop S\nolimits_b {\text{≥}} \mathop S\nolimits_{b - 1} + \mathop P\nolimits_b ,\forall b \in B/\{ 1\} ;$

(7)

$ \quad\quad \mathop C\nolimits_{\max } {\text{≥}} \mathop S\nolimits_b + \mathop P\nolimits_b ,\forall b \in B;$

(8)

$ \quad\quad \mathop X\nolimits_{jb} = 0\;{\rm{or}}\;1{\text{。}}$

(9)

在Model C中，设定分批数量上界 v= n，因为 n个工件最多能分为 n批。式(2)表示目标函数为最小化最大完成时间；式(3)表示每个工件只能属于并必须属于一个批次；式(4)表示各批次中工件的总质量不得超过设备的容量；式(5)表示各批次加工时间取决于装载量和批中工件最大尺寸；式(6)表示各批次的开始加工时间大于批中工件的到达时间；式(7)表示前一批次加工完成后才能开始后一批次的加工，其中 B/{1}表示除第1个批次外的所有批次；式(8)表示所有工件的完成时间必须大于最后一批的完成时间；式(9)表示决策变量的取值范围。

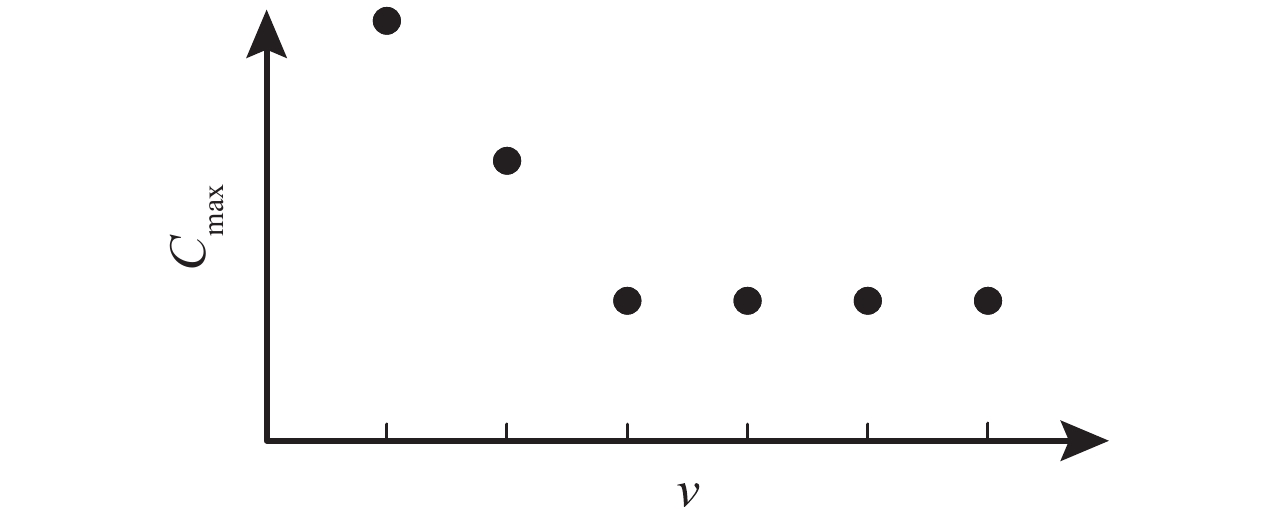
2.2 启发式算法(HC算法)

将Model C中的分批数量上界设定为工件总数量，直接运行数学模型虽然可以得到目标函数的最优解，然而将分批数量上界的值设定得越大，将会产生越多的决策变量和因变量，数学模型的运算效率将会下降。通过大量实验发现，分批数量上界的设定值和Model C的运算结果存在 图1所示的关系特性。

令 C _max( i)表示将分批数量上界设定为 i时的运算结果，该特性可以表述为：如果出现 C _max( i+1)且 i+2≤ n，则必将出现 C _max( i+2)= C _max( i+1)。虽然该特性暂时没有严格的数学证明，但到目前为止还找不到不满足该特性的反例，第Ⅳ节中的所有验证算例也都符合这一特性。

如果工件允许被拆分，那么所有待加工工件至少被分成 $\left\lceil {\sum\limits_{j \in J} {\mathop g\nolimits_j } /\mathop G\nolimits_{\max } } \right\rceil $ 批。运用上文介绍的关系特性，首先将分批数量上界设定为 $\left\lceil {\sum\limits_{j \in J} {\mathop g\nolimits_j } /\mathop G\nolimits_{\max } } \right\rceil $ ，并逐步增大分批数量上界值，反复求解数学模型Model C，直到得到目标函数值最优解。这里将提高Model C运算效率的算法称为HC算法。

HC算法的具体步骤如下。

步骤 1　求解工件的分批数量下界，令 $i \!\!=\!\!\! \left\lceil { \! \sum\limits_{j \in J} {\mathop g\nolimits_j } \!/\!\mathop G\nolimits_{\max } }\! \right\rceil\!\! $ 。

步骤2　设定分批数量上界 v= i，通过数学模型Model C求解目标函数值 $\mathop C\nolimits_{\max } (i)$ 。如果无法得到有效解，令 i= i+1，求解目标函数 C _max( i)；否则，转步骤3。

步骤3　如果 i= n，停止计算， C _max( i)已是目标函数值最优解；否则，令 i= i+1，设定 v= i，求解目标函数值 C _max( i)，转步骤4。

步骤4　如果 C _max( i)= C _max( i–1)，停止计算， C _max( i–1)已是目标函数值最优解；否则转步骤3。

2.3 实验算例

本节通过一个简单的算例来说明数学模型Model C和启发式算法的有效性。

例1　有12个工件需要经过热处理加工，设备的容量为5 kg，工件的到达时间 r _j 、质量 g _j 和尺寸 S _j 如 表1所示。各批次加工时间由式(1)计算可得，其中固定时间系数 α设为0，权重系数 β和 γ分别设为1。

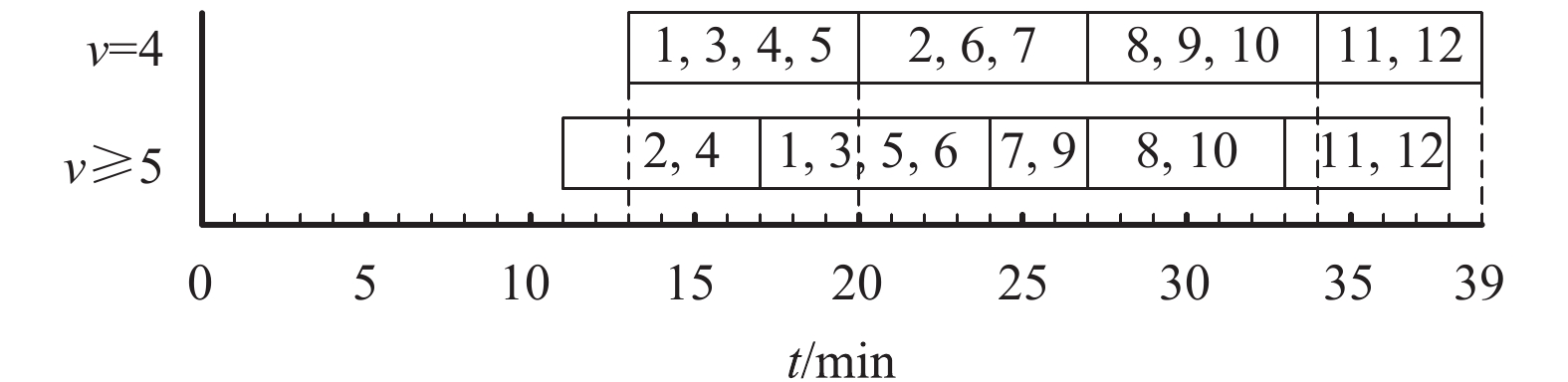
工件的总质量为18 kg，则至少需要分成4批。将分批数量上界 v设置为4, 5, …, 12时，求解Model C得到的调度结果分别为39、38、38、38、38、38、38、38、38 (min)。设置不同分批数量上界，求解Model C得到的调度结果甘特图如 图2所示。从运算结果可以看出，HC算法能够求得该算例的最优解。

3 最小化最大拖期量 3.1 混合整数线性规划数学模型(Model L)

$ \quad\quad {\rm{min }}\mathop L\nolimits_{{\rm{max}}} {\text{。}}$

(10)

s.t.

$ \quad\quad \sum\limits_{b \in B} {\mathop X\nolimits_{jb} } = 1,\forall j \in J;$

(11)

$\quad\quad \sum\limits_{j \in J} {\mathop g\nolimits_j } \mathop X\nolimits_{jb} {\text{≤}} \mathop G\nolimits_{\max } ,\forall b \in B;$

(12)

$ \quad\quad \mathop P\nolimits_b {\text{≥}} \alpha + \beta \sum\limits_{j \in J} {\mathop g\nolimits_j } \mathop X\nolimits_{jb} + \gamma \mathop s\nolimits_j \mathop X\nolimits_{jb} ,\forall b \in B,j \in J;$

(13)

$ \quad\quad \mathop S\nolimits_b {\text{≥}} \mathop r\nolimits_j \mathop X\nolimits_{jb} ,\forall b \in B,j \in J;$

(14)

$ \quad\quad \mathop S\nolimits_b {\text{≥}} \mathop S\nolimits_{b - 1} + \mathop P\nolimits_b ,\forall b \in B/\{ 1\} ;$

(15)

$ \quad\quad \mathop C\nolimits_j {\text{≥}} M(\mathop X\nolimits_{jb} - 1) + \mathop S\nolimits_b + \mathop P\nolimits_b ,\forall b \in B,j \in J;$

(16)

$ \quad\quad \mathop L\nolimits_{\max } {\text{≥}} \mathop C\nolimits_j - \mathop d\nolimits_j ,\forall j \in J;$

(17)

$ \quad\quad \mathop L\nolimits_{\max } {\text{≥}} 0\text{：}$

(18)

$ \quad\quad \mathop X\nolimits_{jb} = 0\;{\rm{or}}\;1{\text{。}}$

(19)

数学模型Model L中，分批数量上界设置为工件总数量。式(10)表示目标函数为最小化最大拖期量；式(11)~(15)与式(3)~(7)相同；式(16)用来计算各工件的完成时间；式(17)用来计算最大拖期量；式(18)表示最大拖期量为非负数；式(19)表示决策变量的取值范围。

3.2 实验算例

本节通过一个简单的实验算例来验证Model L可以求得目标函数值的最优解，并且说明上一章提到Model C所具有的特性并不适用于求解Model L。即当出现 L _max( i+1)= L _max( i)且 i=2≤ n时， L _max( i+2)= L _max( i+1)不一定成立，其中 L _max( i)表示将分批数量上界设定为 i时Model L的运算结果

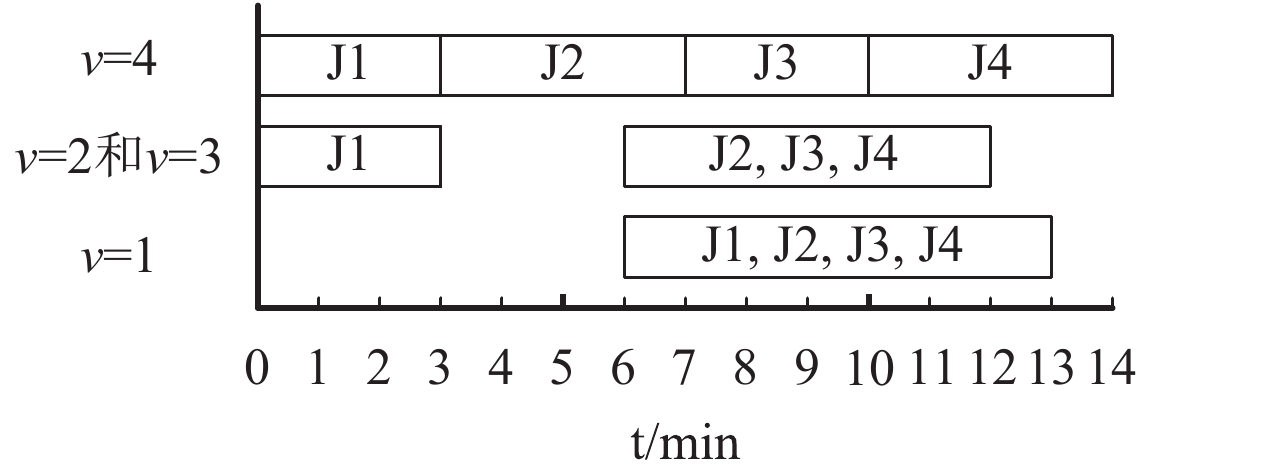
例2　有4个工件(J1, J2, J3, J4)需要经过热处理加工，各工件质量都为1，尺寸分别为(1, 2, 1, 2)，到达时间分别为(0, 3, 6, 6)，交货期分别为(3, 10, 10, 13)，设备的容量为4 kg。算例中时间的单位均为min，质量的单位为kg，尺寸的单位为mm，固定时间系数 α设定为1，权重系数 β和 γ也分别设定为1。通过设定不同的分批数量上界，求解Model L得到的调度结果如 图3所示。

通过 图3可以看出，当分批数量上界 v设定为2或者3时，运行Model L将得到相同的调度结果，此时最大拖期量 L _max(3)= L _max(2)=2 min。但是最优调度结果出现在分批数量上界设定为4时，最大拖期量 L _max(4)=1 min。

3.3 启发式算法(HL算法)

从上一节的算例可以看出，上一章构造的启发式算法并不适用于数学模型Model L。目前计算机的运算速度并不能满足Model L求解大规模调度问题，本节将构造适用于求解大规模问题的近优解启发式算法，这里将该构造启发式算法称为HL算法。

先到先加工FCFS(first come first served)和最早交货期先加工EDD(earliest due date)是目前批调度中常见的两种规则算法。这2种规则算法对不同调度环境各有优劣，本节将构建一种综合考虑到达时间和交货期的调度算法，以适用不同的调度环境。当工件到达的时间强度较低时，为了避免设备长时间处于等待状态，算法中将设定一个设备最大等待时间，设备最大等待时间的值设为各批次预期平均加工时间的1/3。当空闲设备达到最大等待时间，则在已到达工件中选择工件立即开工。

HL算法具体步骤如下。

步骤1　将所有工件按到达时间非降排序，并将工件依次放到集合 K中。设 L _max(OS)为已经得到的最优调度结果，并令 L _max(OS)的初始值为一个较大数值。

步骤2　按工件在集合 K中的顺序依次组批，使各批次尽可能装满，每个批次只考虑在设备最大等待时间前到达的工件，组批完毕后转步骤3。

步骤3　计算最大拖期量 L _max。如果 L _max=0，则令 L _max(OS)= L _max，转步骤6；否则转步骤4。

步骤4　如果 L _max≤ L _max(OS)，则令 L _max(OS)= L _max，转步骤5；否则转步骤6。

步骤5　找出拖期量最大的工件J1，在集合 K中从J1的位置开始往前搜索，如果出现工件J2的交货期大于J1，则停止搜索，更新集合 K中的工件顺序，将J2紧接在J1后面，转步骤2；否则如果不存在交货期大于J1的工件，则转步骤6。

步骤6　停止运算，最大拖期量为 L _max(OS)，输出 L _max(OS)对应的调度结果。

定理1 　HL算法的计算复杂度为 $O(\mathop n\nolimits^2 \log n)$ 。

证明 　步骤1为工件排序，计算复杂度为 O( nlog n)；步骤2到步骤6中，每次重新排序计算复杂度为 O( nlog n)。在最坏情况下，每个工件都必须调整顺序，则计算复杂度为 O( n ²log n)；在每次重新排序后为工件组批的计算复杂度为 O( n)。在最坏情况下，需要进行 n次组批，则计算复杂度为 O( n ²)。因此HL算法的计算复杂度为 O( n ²log n)。证毕。

4 算法验证

本章的实验分成3部分。第1部分对比说明数学模型Model C和HC算法的运算效率；第2部分检验数学模型Model L的运算时间和HL算法的偏差百分比；第3部分通过和其他典型算法比较，说明HL算法的有效性。用于实验的计算机配置为Pentium(R) Dual-core CPU T4200 @2.00 GHz，数学模型运算工具为CPLEX 12.3，MATLAB 7.0作为运行HL算法的运算工具。实验数据参数通过以下方式随机产生。

工件质量( g _j )：服从均匀分布 U[10, 50](kg)，工件平均质量 $\overline {\mathop g\nolimits_j } = 30\;{\rm{kg}}$ ；

工件尺寸( s _j )：2 g _j (mm)；

设备容量( G _max)：200 kg，300 kg和400 kg；

工件到达时间强度：0.8；

各批次的加工时间由式(1)计算得到，其中固定时间系数 α设为0，权重系数 β和 γ分别设为1.2和3，则各批次平均加工时间 $\overline {\mathop P\nolimits_b } = 0.96\mathop G\nolimits_{\max } + 180$ (min)；

工件到达间隔时间： $\lambda = \displaystyle\frac{{\overline {\mathop P\nolimits_b } }}{{0.8}} \times \frac{{\overline {\mathop g\nolimits_j } }}{{\mathop G\nolimits_{\max } }}$ (min)；

工件到达时间( r _j )：服从平均分布 U[0, n λ](min)；

工件交货期( d _j )： $\mathop r\nolimits_j + {\rm{rand}}\;{\mathop{\rm int}} (300,1\,000)$ (min)。

实验1 　设置13种不同的工件数量，分别为10, 11, 12, 13, 14, 15, 16, 17, 18, 30, 40, 50和60。对每个参数组合随机产生20组数据进行实验，并对20组数据的实验结果取平均值记录于 表2和 表3中。其中 表2记录了将分批数量上界 v设置为工件数量 n直接求解数学模型Model C，平均每次所需要的运算时间； 表3记录了HC算法每次运行平均需要调用Model C的次数和相应的平均运算时间。对于本实验的所有算例，直接求解数学模型和HC算法都能得到最优调度结果。

当设置 v= n直接求解数学模型Model C，目前计算机在1 h内只能求解不大于18个工件的调度问题。通过 表2可以看出，随着工件的增多，每次Model C的运算时间将急剧上升，当有18个工件时，每次Model C的运算时间将高达1 000 s左右。随着设备容量的增大，Model C的运算效率也逐渐下降，这是由于每个批次能容纳越多工件，数学模型在做计算时要做越多的搜索。对比 表2和 表3可以发现，HC算法能明显提高求解效率，当工件数量不大于18个时，对于不同设备容量HC算法求得最优解的平均总运算时间都不大于15 s。

通过观察 表3可以发现，当工件数量不大于18个时，不同设备容量对HC算法的运算效率影响并不大。当工件数量大于30个时，设备容量越大HC算法的运算效率越高。这是由于设备容量越大，工件的分批数量也就越少，Model C的单次运算时间也就越短，并且求得最优解需要调用Model C的次数也随着设备容量增大而减少。随着设备容量的增大，HC算法能求解的调度规模也逐渐增大。当设备容量为400 kg，即每个批次平均大约能容纳13个工件时，HC算法求解50个工件的调度问题总运算时间不超过200 s，求解60个工件的总运算时间不超过1 h。

实验2 　设置8种不同工件数量，分别为10, 11, 12, 13, 14, 15, 16和17。对每种参数组合分别产生20组数据，其运行结果取平均值。数学模型Model L的运算时间记录于 表4中。HL算法的偏差百分比记录于 表5中。HL算法的偏差百分比RE(radio error)定义为， ${\rm{RE}} = \displaystyle\frac{{100 \times \left[ {\mathop L\nolimits_{\max } ({\rm{HL}}) - \mathop L\nolimits_{\max } (*)} \right]}}{{\mathop L\nolimits_{\max } (*)}}$ ，其中， L _max(HL)表示算法HL得到的目标函数值； L _max $(*) $ 表示最优解。

基于目前的计算机运算水平，数学模型Model L在1 h内只能求解18个工件以下的调度问题。从 表4可以看出，随着调度规模的最大，Model L需要的运算时间呈指数增长；并且设备容量越大，Model L需要越长运算时间，这是由于各批次能容纳工件数量越多，计算时需要做越多搜索。

通过 表5可以发现，随着调度规模的增大，HL算法的调度性能明显越来越好，这是由于HL算法在调度规模较小时出现较坏调度结果的偶然性较大。当工件数量为17时，HL算法的平均偏差不超过15%。设备容量对HL算法的调度性能影响不大。

实验3 　设置5种不同工件数量，分别为100、200、300、400和500。对每种参数组合分别产生100组数据，分别通过EDD规则、FCFS规则和HL算法进行运算，并将其性能率PR(performance radio)取平均值记录于 表6中。例如，HL算法的性能率定义为： ${\rm{PR}}({\rm{HL}}) = \displaystyle\frac{{100 \times \left[ {\mathop L\nolimits_{\max } (HL) - \mathop L\nolimits_{\max } (\mathop B\nolimits^* )} \right]}}{{\mathop L\nolimits_{\max } (\mathop B\nolimits^* )}}$ ，其中 L _max(HL)表示HL算法计算得到的目标函数值； L _max( B ^*)表示对同一组数据，这3种算法计算得到的目标函数值中的最小值。

实验3中各组数据在3种算法中的运算都不超过0.02 s，因此本实验主要只对比3种算法计算结果的优劣。通过 表6可以看出，对于不同参数组合，HL算法的运算结果明显优于其他两种算法，并且工件数量越少HL算法的优势越明显。当工件数量小于300时，设备容量越小HL算法的优势越明显。FCFS规则的运算结果总体略优于EDD规则。

5 结束语

本文根据热处理批加工时间受到装炉量和批中最大工件尺寸双重约束的特点，分别构建以最小化最大完成时间和以最小化最大拖期量为调度目标的数学模型Model C和Model L。根据分批数量上界设定值与Model C运算结果的关系特性，构建了启发式算法(HC算法)来提高Model C的运算效率。通过一个简单反例说明Model C所具有的特性并不适用于求解Model L，并提出启发式算法(HL算法)来求解以最小化最大拖期量为目标的调度问题，HL算法的计算复杂度为 O( n ²log n)。

实验结果显示，数学模型Model C、Model L和HC算法都能够得到问题的最优解。将分批数量上界设置为工件总数量，直接求解Model C和Model L，在1 h内只能分别求得18个工件和17个工件调度问题的最优解。而HC算法能够在1h内得到60个工件调度问题的最优解，并且设备容量越大，调度规模也就越大。对于500个工件的调度问题，HL算法的运算时间不超过0.02 s。对于17个工件调度问题，HL算法和最优解相比平均偏差不超过15%，而对于大规模调度问题，HL算法的调度性能明显优于其他两种典型算法。

基于本文的研究，后续将继续研究加工时间受双重约束的批调度问题，并主要从以下两方面开展：1)存在平行批处理机的批调度问题；2)存在不相容工件族的批调度问题。