机器人避障路径规划是指在障碍物存在的情况下,从起始点到目标状态的无碰撞路径。在机械臂运动的过程中,不仅要避免机械臂末端与障碍物发生碰撞,同时能够防止杆端与障碍物产生碰撞,使得机械臂的避障路径规划与一般的移动机器人避障规划相比状态空间维数更高,更具复杂性。
机械臂的避障路径规划有两种:全局路径规划以自由空间法[1- 3]为代表,该方法需要预先得到全局的信息,计算量比较大;局部路径规划方法有神经网络[4]、蚁群算法[5]等,这类方法由于缺乏全局信息,往往容易陷入局部极小值。因此,很有必要结合使用全局与局部规划算法,充分发挥各自算法的优点[6- 7]。
人工势场法是一种局部路径规划算法,具有结构简单,在静态环境中适应性强的优点,但容易陷入局部极小,或在障碍物周围振荡的缺陷。针对这些不足,国内外许多学者对人工势场法进行了不同程度的改进。文献[8]运用几何法与人工势场法相结合解决传统人工势场法的局部极小值陷阱问题。然而,在对机械臂整体进行路径规划时,运用了逆运动学的方法,该方法需要从8组解中进行筛选,效率比较低。文献[9]在陷入局部极小值时,通过添加虚拟障碍物改变整个人工势场解决问题。该方法的实现必须在通过其他的方法得到一组“合理”的关节角度解,但在实时应用中难以选取“合理”的解。文献[10]在处理局部极小值点问题时,在该点的最速下降方向上引入虚拟目标点,把当前点吸引过去,从而逃离了局部最小值点。然而,运用几何方法确定的虚拟目标点仅适用于简单的环境之中。
基于以上分析,改进人工势场法的思路主要是建立虚拟目标点、增加虚拟障碍物、改变势函数、建立等势线法[11]等。本文从建立虚拟目标点的思路出发,将人工势场法与改进的快速扩展随机树算法结合起来使用。首先利用人工势场法对机械臂进行局部的路径规划,当机械臂陷入局部极小值时,快速扩展随机树算法开始工作,确定临时目标点,绕开局部极小值点。当机械臂逃离局部极小值点到达临时目标点时,切换回人工势场法进行规划。通过人工势场法与改进RRT算法的混合切换使用,最后能够到达目标点。
1 环境建模 1.1 机械臂运动学模型本文采用德国库卡公司的youBot机械臂作为研究对象。该机械臂由一个直流电机驱动的5轴机械臂以及一个二指的末端执行器组成[12],具体运动参数如 图1所示。

|
图 1 youBot机械臂结构 Fig. 1 The mechanical of youBot robot arm |
根据 图1的运动参数,采用标准D-H法建立运动学模型。D-H参数见 表1。
| 表 1 机械臂D-H模型参数表 Tab. 1 The denavit- hartenberg parameter table of the robot arm |
为了简化表达,本文将sin( θ n )记作 s n ,cos( θ n )记作 c n 。其中, θ n 表示第 n个关节的关节角, d n 表示第 n个关节的连杆偏距, a n 表示第 n个关节的连杆长度, α n 表示第 n个关节的连杆转角。
根据 表1 中的参数和式(1)可以得到机械臂的总变换矩阵,即机械臂的正运动学模型,见式(2)。
| $\begin{aligned}& \quad\quad{ {A}_i} = { {R}_{i - {\rm{1}}}}\left( {{\theta _i}} \right){ {T}_{i - {\rm{1}}}}\left( {{d_i}} \right){ {T}_{i - {\rm{1}}}}\left( {{a_i}} \right){ {R}_{i - {\rm{1}}}}\left( {{\alpha _i}} \right) = \\ & \left[ {\begin{array}{*{20}{c}} {{c_i}} & { - {s_i}c{'_i}} & {{s_i}s{'_i}} & {{a_i}{c_i}}\\{{s_i}} & {{c_i}c{'_i}} & { - {c_i}s{'_i}} & {{a_i}{s_i}}\\{\rm{0}} & {s{'_i}} & {c{'_i}} & {{d_i}}\\{\rm{0}} & {\rm{0}} & {\rm{0}} & {\rm{1}}\end{array}} \right]{\text{。}}\end{aligned}$ | (1) |
对于当前坐标系 X i-1 - Z i-1 和下一个坐标系 X i - Z i ,其中,矩阵 R i ( θ i )表示将 Z i-1 轴旋转 θ i ,使得 X i-1 与 X i 平行;矩阵 T i-1 ( d i )表示沿 Z i-1 轴平移 d i 的距离,使得 X i-1 和 X i 共线;矩阵 T i-1 ( a i )表示沿 X i-1 轴平移 a i 的距离,使得 X i-1 轴和 X i 轴的原点重合;矩阵 R i-1 ( α i )表示将 Z i-1 轴绕 X i 轴旋转 α i ,使得 X i-1 轴和 X i 轴的原点重合;4个矩阵 R i-1 ( θ i )、 T i-1 ( d i )、 T i-1 ( a i )、 R i-1 ( α i) 相乘表示机械臂相邻关节角之间由一个参考坐标系到另一个参考坐标系的坐标变换。为了简化表达,将cos( α i )记作 c’ i ,将sin( α i )记作 s’ i 。 i表示坐标系的下标,对于youBot机械臂模型,取值范围为1~5。
| $\quad\quad {{A} = {{A}_{\rm{1}}}{{A}_{\rm{2}}}{{A}_{\rm{3}}}{{A}_{\rm{4}}}{{A}_{\rm{5}}}}{\text{。}}$ | (2) |
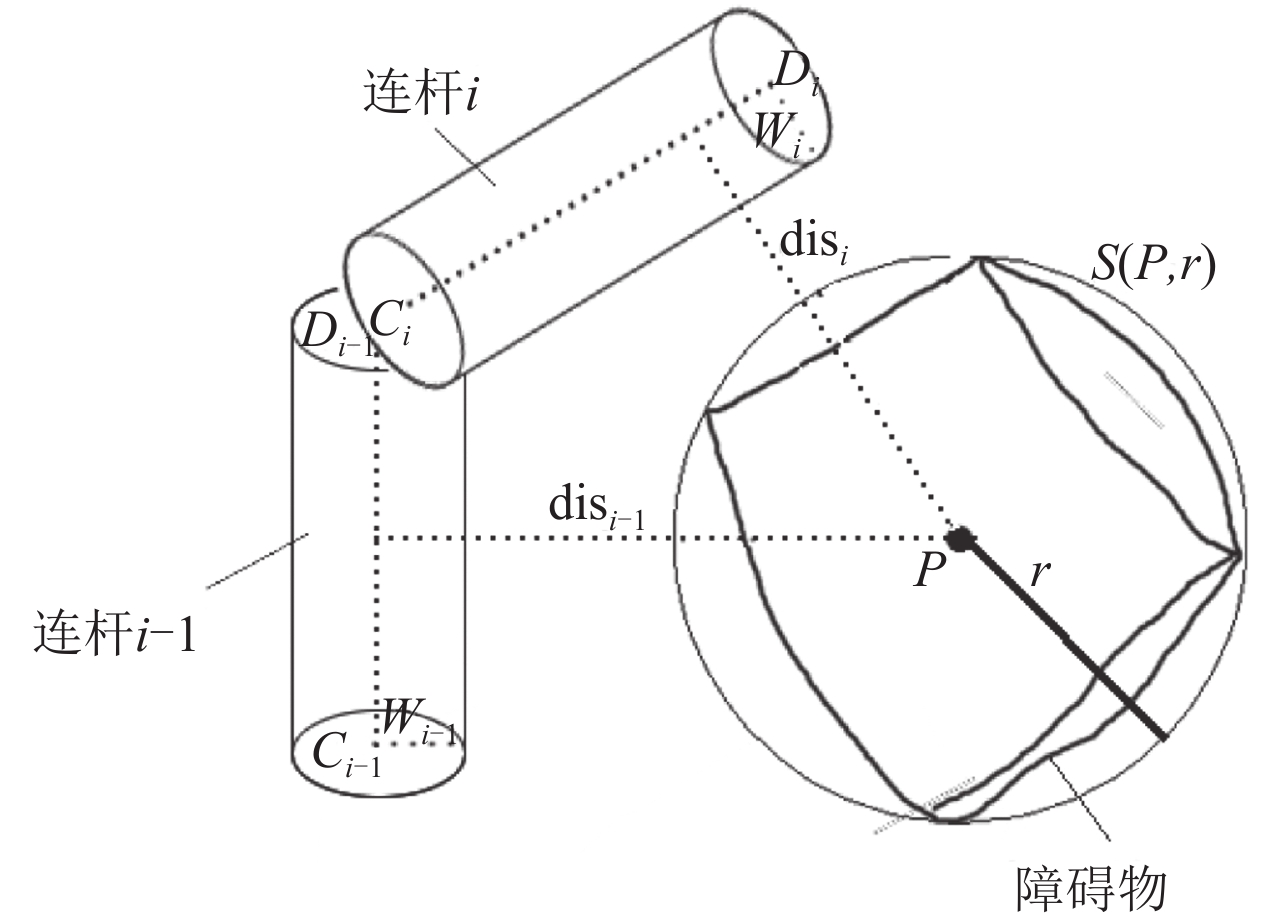
在现实环境中,障碍物通常比较复杂,难以通过精确的公式描述。本文利用球体包围障碍物近似模拟。该方法尽管增加了障碍物区域,但极大地简化了对障碍物的描述,因此能提高避障路径规划的效率。以球形包络 S( P, r)描述障碍物,其中, P( X, Y, Z)为球心世界坐标, r为球半径,具体模型如 图2所示。
|
图 2 障碍物的球形包络碰撞检测模型 Fig. 2 Spherical envelope collision detection model of obstacle |
本文将障碍物用球形包围盒来模拟,将机械臂连杆用圆柱体来模拟。因此,机械臂的碰撞检测问题转化为线段和球体之间的碰撞检测。
假设机械臂连杆 i的两端为 C i , D i ,连杆圆柱体底面半径为 W i ,球形包络障碍物的球心为 P( X, Y, Z),半径为 r,因此,碰撞检测问题可以简化为球心 P到线段 CD的距离dis i 。
1)如果dis i < r+ W i ,则表示机械臂连杆 i与障碍物发生碰撞;
2)如果dis i ≥ r+ W i ,则表示机械臂连杆 i没有与障碍物发生碰撞。
分别检测机械臂的连杆1~ m( m为机械臂关节数),确定整个机械臂是否与障碍物发生碰撞。
2 算法原理 2.1 机械臂的人工势场法原理人工势场法是局部路径规划方法[13],最早是针对移动机器人进行避障使用的,通常使用如下的引力势函数和斥力势函数:
| $\quad\quad {{U_{{\rm{att}}}}({P_{{\rm{robot}}}}) = \frac{1}{2}}{k_{\rm{a}}}|{P_{{\rm{robot}}}} - {P_{\rm{g}}}{|^2}{\text{。}}$ | (3) |
式中, U att( P robot)表示引力势函数, k a代表引力常数, P robot代表机器人的当前位置, P g代表目标点的位置。斥力势函数
| $\quad\quad {U_{{\rm{rep}}}} = \left\{ {\begin{array}{*{20}{c}}{\displaystyle\frac{1}{2}{k_r}{{(\frac{1}{l} - \frac{1}{{{l_0}}})}^2},} & {l {\text{≤}} {l_0};}\\{0,}\,\,\,\,\qquad\qquad\qquad & {l {\text{>}} {l_0}{\text{。}}}\end{array}} \right.$ | (4) |
式中, U rep表示斥力势函数, k r代表斥力常数, l代表机器人与障碍物之间的距离, l 0代表斥力场的作用范围。
对于机械臂当前关节角Theta i =( θ 1, θ 2, θ 3, θ 4, θ 5),通过运动学方程可求出机械臂末端点 P robot,假设目标点为 P g。于是可以引用式(3)作为引力势函数。
在工业机械臂上使用斥力势函数的情况复杂得多。由于机械臂的避障同时要求机械臂末端与杆端都不能与障碍物发生碰撞,因此机械臂的斥力势能函数需要计算每个连杆与障碍物的距离,要对每个关节分别进行考虑。对于每个关节 i,斥力势能函数为
| $\quad\quad {U_{ir}} = \left\{ {\begin{array}{*{20}{c}}{\displaystyle\frac{1}{2}{k_r}{{(\frac{1}{{{l_n}}} - \frac{1}{{{l_0}}})}^2},} & {{l_n}{\text{≤}} {l_0};}\\{0,}\,\, \,\,\,\qquad\qquad\qquad& {{l_n} {\text{>}} {l_0}{\text{。}}}\end{array}} \right.$ | (5) |
式中, k r代表斥力常数, l n代表连杆与障碍物之间的距离, l 0代表斥力场的作用范围。
整个机械臂的斥力势能为
| $\quad\quad {U_{{\rm{rep}}}} = \sum\limits_{i = 1}^n {{U_{ir}}}{\text{。}}$ | (6) |
对于每一时刻,机械臂受到的总势能为引力势能与斥力势能的总和,即
| $\quad\quad {U = {U_{{\rm{att}}}}} + {U_{{\rm{rep}}}}{\text{。}}$ | (7) |
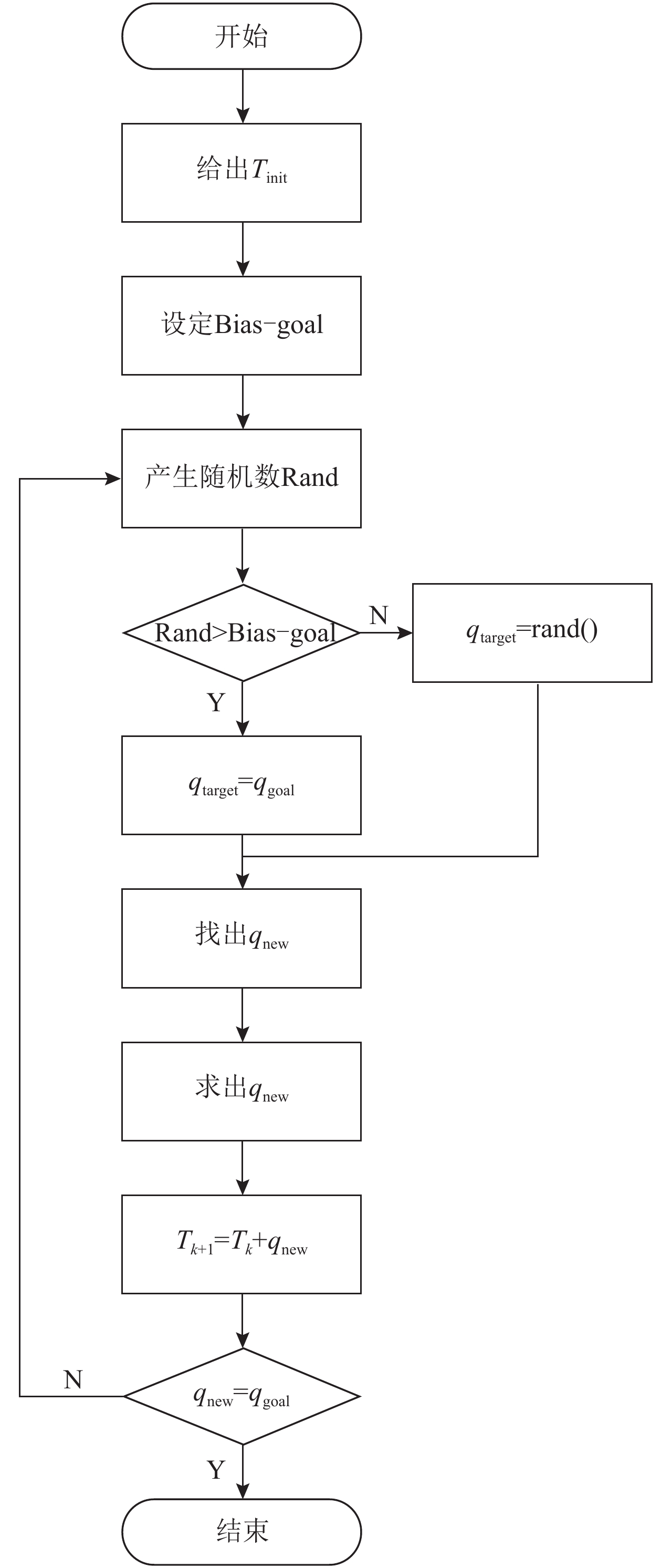
快速扩展随机树算法是由LaValle[14]教授提出的。由于它是一种随机算法,不可避免地存在扩展方式过于平均,规划的路径质量不高,算法实时性差等缺点。针对以上缺点,本文通过吸收启发式算法的经验,对原有算法进行了改进,使树向目标点方向生长。这样会提高搜索的实时性,同时也会相应地提高规划路径的质量。具体算法如 图3所示。
|
图 3 改进的RTT算法流程图 Fig. 3 The flow chart of improved RTT algorithm |
具体算法描述如下。
1)求出 q start。
2)求出 q target。
3)找到 q near, q near是距离 q target最近的节点。
4)求出 q new, q new在 q near与 q target的连线上,必须在机械臂可达空间内且与 q near的距离为γ。如果 q new存在,转到步骤5);否则,转到步骤2)。
5)在 T k 上增加一个叶子节点 q new。
6)判断条件新增的叶子节点 q new是不是为目标点 q goal,若是,求解完成,结束算法;否则,转到步骤2)。
其中, q start表示起始点, q goal表示目标点, γ表示步长, T k 表示树上有 k个节点, q new的计算可由式(8)~(10)得出。
| $\begin{split}{x_{{q_{{\rm{new}}}}}} = & {x_{{q_{{\rm{near}}}}}} + \\& \displaystyle\frac{{\gamma ({x_{{q_{{\rm{near}}}}}} - {x_{{q_{{\rm{target}}}}}})}}{{\sqrt {{{({x_{{q_{{\rm{near}}}}}} - {x_{{q_{{\rm{target}}}}}})}^2} + {{({y_{{q_{{\rm{near}}}}}} - {y_{{q_{{\rm{target}}}}}})}^2} + {{({z_{{q_{{\rm{near}}}}}} - {z_{{q_{{\rm{target}}}}}})}^2}} }},\end{split}$ | (8) |
| $\begin{split}{y_{{q_{{\rm{new}}}}}} = & {y_{{q_{{\rm{near}}}}}} + \\& \displaystyle\frac{{\gamma ({y_{{q_{{\rm{near}}}}}} - {y_{{q_{{\rm{target}}}}}})}}{{\sqrt {{{({x_{{q_{{\rm{near}}}}}} - {x_{{q_{{\rm{target}}}}}})}^2} + {{({y_{{q_{{\rm{near}}}}}} - {y_{{q_{{\rm{target}}}}}})}^2} + {{({z_{{q_{{\rm{near}}}}}} - {z_{{q_{{\rm{target}}}}}})}^2}} }},\end{split}$ | (9) |
| $\begin{split}{z_{{q_{{\rm{new}}}}}} = & {z_{{q_{{\rm{near}}}}}} + \\& \displaystyle\frac{{\gamma ({z_{{q_{{\rm{near}}}}}} - {z_{{q_{{\rm{target}}}}}})}}{{\sqrt {{{({x_{{q_{{\rm{near}}}}}} - {x_{{q_{{\rm{target}}}}}})}^2} + {{({y_{{q_{{\rm{near}}}}}} - {y_{{q_{{\rm{target}}}}}})}^2} + {{({z_{{q_{{\rm{near}}}}}} - {z_{{q_{{\rm{target}}}}}})}^2}} }}{\text{。}}\end{split}$ | (10) |
q target为随机树生成过程中的局部目标点,其构造方式影响着随机树的形状。本文采用随机函数加参数 q goal-Possibility结合共同生成局部目标点。确定 q target的方法如下:
人工设定参数 q goal-Possibility,表示算法中选取目标点 q goal为 q target的可能性。如果 q goal-Possibility的值大于算法产生的随机数的时候就选取目标点 q goal作为 q target,否则随机生成一个点当作 q target。
3 改进RRT与人工势场法混合算法 3.1 人工势场法的局部最小值问题人工势场法把所有信息归结于引力与斥力的合力,并以合力的方向指示机械臂下一步的运动。由于机械臂在运动过程中只能感知到附近的障碍物,缺乏全局的障碍物信息,因此,机械臂在避障过程中容易陷入局部极小值点,或者在局部极小值点附近循环跳动。
3.2 快速扩展随机树的效率问题由于快速扩展随机树是由随机函数产生的,重复执行同一任务会得到不同的路径。同时,由于快速扩展树的叶子节点也是随机生成的,缺乏指向性,因此规划出的路径往往并不是最优路径。
3.3 改进的RRT算法与人工势场法结合的混合算法 设计算法结合在避障路径规划研究中的作用非常明显:针对一种算法的缺点与不足采用另外一种算法来进行弥补与改进。由于人工势场法缺乏全局信息,极易陷入局部极小点,因此,可用快速扩展随机树算法作为补充;同样,快速扩展随机树算法的实时性很差,也需要与人工势场法进行结合。
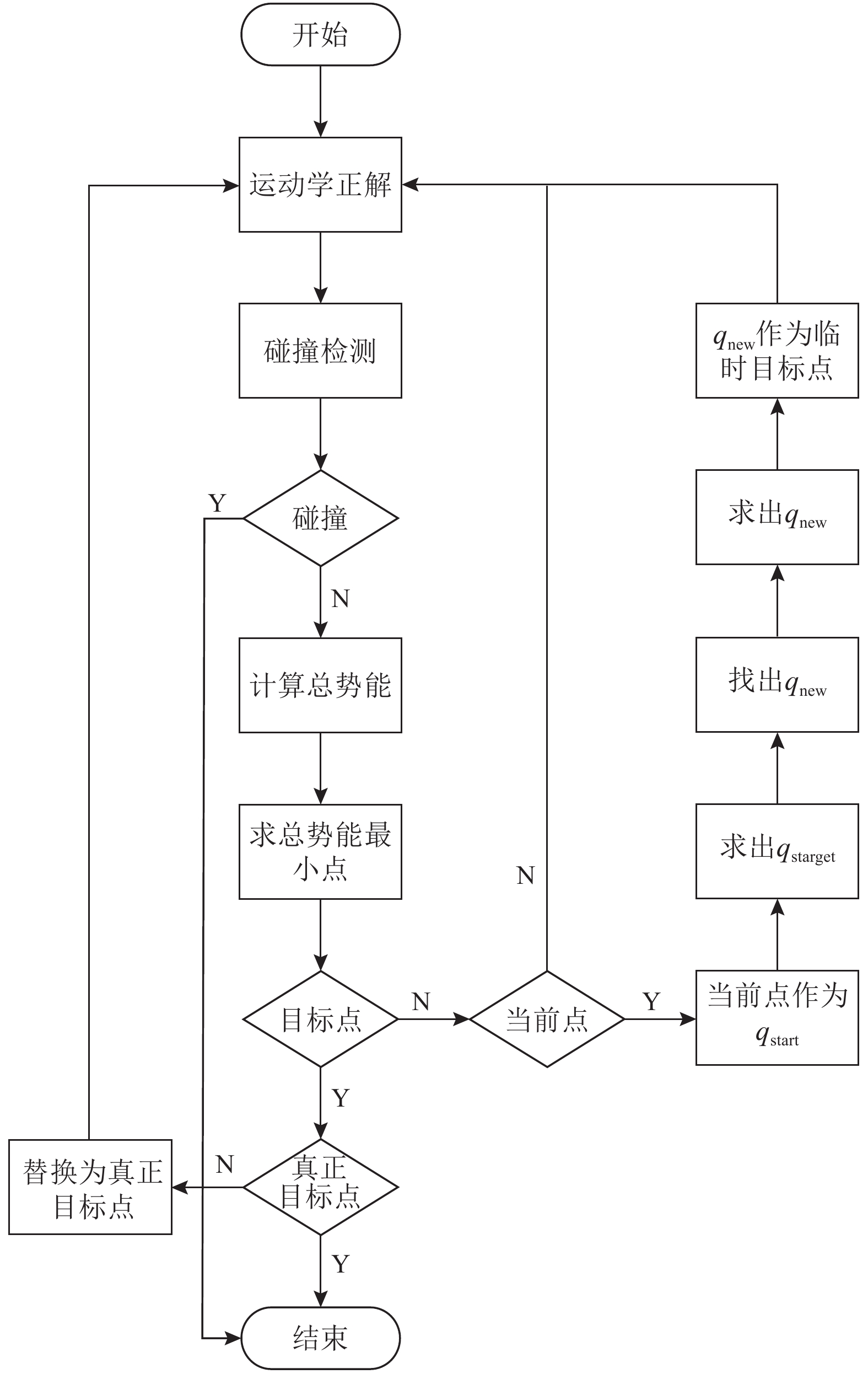
本文在移动机器人避障路径规划算法[15]启发下,改进类似算法并且应用到工业机械臂当中。通过人工势场法进行局部规划,用改进的RRT算法进行全局规划,当人工势场法陷入局部极小点的时候采用改进RRT算法进行全局规划。机械臂沿着改进的RRT算法规划的全局路径运动,就能逃离局部极小值点。只要机械臂能逃离局部极小值点,切换回人工势场法重新规划路径,就能最终完成任务。具体算法过程如 图4所示。
|
图 4 改进RRT算法与人工势场法结合的混合算法流程 Fig. 4 The process of the combination of artificial potential field and improved RRT algorithm |
1)获取当前关节角的相邻关节角。相邻关节角是当前每个关节角取 θ- λ, θ, θ+ λ 3种情况,其中 λ为搜索步长。
2)通过运动学正解求出末端执行器的坐标,同时得到机械臂每节连杆两端的坐标。
3)将第2)步得到的每节连杆与障碍物进行碰撞检测。若碰撞则舍弃当前关节角,否则计算连杆与障碍物的距离以及机械臂末端与目标点的距离。
4)将第3)步计算出的距离代入式(3)和式(5)中,分别计算斥力势能和引力势能。
5)得到斥力势能和引力势能之和最小时对应的相邻关节角。对末端点进行判断,如果末端点是目标点,则转到第6)步;否则,转到第7)步。
6)判断目标点是真正目标点还是临时目标点。如果是真正目标点,则机械臂完成避障;否则,把目标点替换为真正目标点,并跳转到第1)步。
7)判断第5)步的相邻关节角是否是当前关节角。如果不是当前关节角,则机械臂运动到这个关节角,然后跳转到第1)步。如果是当前关节角,则进入第8)步跳出局部极小值点。
8)按照 图3改进RRT算法流程,分别依次求出 q target, q near, q new,将 q new作为临时目标点,然后跳转到第1)步。
4 数值仿真实验为验证文中算法的有效性,使用Matlab进行仿真实验。实验从起始位置运动到目标位置,机械臂成功到达目标点且运动过程中机械臂杆端与末端都没有跟障碍物发生碰撞,说明机械臂避障成功。
设置机械臂运动控制参数如 表2所示。
| 表 2 机械臂运动控制参数表 Tab. 2 The motion control parameter table of robot arm |
实验1 算法对变化的障碍物的适应性实验。
本实验人为设定机械臂末端的初始坐标以及目标点坐标,通过多次实验,在每次实验得到的末端运动轨迹附近增加障碍物,增加下一次机械臂避障运动规划的难度,得到的结果如 图5所示。

|
图 5 存在障碍物环境下的机械臂末端轨迹 Fig. 5 The trajectory of the robot arm in the environment with obstacles |
由 图5可以看出,随着障碍物数量增加,机械臂的工作环境变得复杂,但使用改进RRT与人工势场法混合算法机械臂依然能够顺利完成避障,而且避障轨迹比较平滑。对比 图5(d)与 图5(e),当障碍物的位置发生变化时,机械臂依然能够完成避障,说明该算法能够适应环境的变化。
实验2 与类似算法进行避障成功率比较。
本实验通过使用随机函数随机生成障碍物与目标点,在控制其他变量都相同的情况下,用障碍物的数量表示周围环境的复杂程度,通过与文献[10]所使用的方法在相同搜索步长下比较机械臂规划的运行步数,结果如 表3和 表4所示。表中,∞表示该实验无法到达目标点。
| 表 3 使用本算法在不同数量障碍物的环境下机械臂运行步数比较 Tab. 3 Using this algorithm in different number of obstacles under the environment of mechanical arm operation steps |
| 表 4 使用文献[10]所用算法在不同数量障碍物的环境下机械臂运行步数比较 Tab. 4 Using the algorithm for document [10] in different number of obstacles under the environment of mechanical arm operation steps |
对比 表3和 表4可以看出,在障碍物数量只有1个或者2个的简单环境中,2种算法的运行步数基本相同,存在个别实验中本算法运行步数比文献[10]所使用算法多。本算法并不一定规划出最优的路径,但总体上规划都能成功且机械臂的运行步数比较少,说明本算法在简单环境中有效。在障碍物数量为3个或者4个的复杂环境中,本算法的优越性就能体现出来。在有着3个障碍物的环境中,文献[10]所使用算法有3次规划路径失败,而本实验只有1次失败,说明本算法在复杂环境下依然有较高的适应性。在有着4个障碍物进一步复杂的环境下,文献[10]所使用算法规划的成功率急速降低,而本算法虽然有时候规划的步数较高,但依然保持路径规划有着较高的成功率。
5 实际应用实验 5.1 虚拟仿真实验本实验在机器人操作系统(ROS)里面的Rviz软件进行可视化仿真。首先,通过编写URDF文件搭建环境模型,然后使用本算法控制机械臂进行避障路径规划,规划过程的关键点如 图6所示。可以看出,机械臂从起始状态( 图6(a))开始通过把关节3和关节4“向上提”到达中间状态( 图6(b))避开障碍物,最后顺利到达目标点( 图6(c))。

|
图 6 避障路径规划仿真过程 Fig. 6 The simulation process of Obstacle Avoidence Path Planning |
根据仿真环境在现实环境中搭建环境模型,用长方体盒子作为障碍物,用毛绒玩具作为目标点并且以末端执行器夹住毛绒玩具为实验目标进行实际实验。把本算法移植到机械臂运动规划模块当中,结果如 图7所示。可以看出,利用RRT与人工势场混合算法,机械臂能够顺利完成任务,该实验验证了虚拟仿真的结果。

|
图 7 实际环境下的避障路径规划过程 Fig. 7 The path planning process of obstacle avoidance in real environment |
本文将改进RRT算法与人工势场法结合使用,在关节空间内,对机械臂的避障路径规划进行研究,通过实验证明该混合算法在避障过程中有效避免了机械臂杆端和末端与障碍物发生碰撞。算法运行过程简单,能够适应环境的变化,在复杂的环境下依然有效,满足机械臂避障的要求。通过进行实际实验表明了实际与仿真实验的一致性。
| [1] | LOZANO-PEREAZ T. Spatial planning: a configuration space approach[J]. IEEE Transaction on Computers, 1983, 32(2): 108-120. |
| [2] | LOZANO-PEREAZ T. A simple motion-planning algorithm for general robot manipulator[J]. IEEE Journal of Roboties and Automation, 1987, 3(3): 224-238. DOI: 10.1109/JRA.1987.1087095. |
| [3] | LOZANO-PEREAZ T. Automatic planning of manipulator transfer movements[J]. IEEE Transaction on System Man and Cybernetics, 1981, 11(10): 681-698. DOI: 10.1109/TSMC.1981.4308589. |
| [4] |
钱夔, 宋爱国, 章华涛, 等. 基于自适应模糊神经网络的机器人路径规划方法[J].
东南大学学报(自然科学版), 2012, 42(4): 637-624.
QIAN Kui, SONG Aiguo, ZHANG Huatao. Path planning for mobile robot based on adaptive fuzzy neural network[J]. Journal of Southeast University(Natural Science Edition), 2012, 42(4): 637-624. DOI: 10.3969/j.issn.1001-0505.2012.04.012. |
| [5] |
周东健, 张兴国, 马海波, 等. 基于栅格地图-蚁群算法的机器人最优路径规划[J].
制造业自动化, 2013, 36(3): 91-94.
ZHOU Dongjian, ZHANG Xingguo, MA Haibo. Optimal path planning for mobile robot based on grid map with ant colony algorithm[J]. Manufacturing Automation, 2013, 36(3): 91-94. |
| [6] |
贾庆轩, 陈钢, 孙汉旭, 等. 基于A
*算法的空间机械臂避障路径规划
[J].
机械工程学报, 2010, 46(13): 109-115.
JIA Qingxuan, CHEN Gang, SUN Hanxu. Path planning for space manipulator to avoid obstacle based on A * algorithm [J]. Journal of Mechanical Engineering, 2010, 46(13): 109-115. |
| [7] |
李爱萍, 李元宗. 机器人路径规划方法的研究[J].
机械工程与自动化, 2009(10): 194-197.
LI Aiping, LI Yuanzong. Research on path planning method of robot[J]. Mechanical Engineering and Automation, 2009(10): 194-197. |
| [8] |
汪首坤, 朱磊, 王军政. 基于导航势函数法的六自由度机械臂避障路径规划[J].
北京理工大学学报, 2015, 35(2): 186-191.
WANG Shoukun, ZHU Lei, WANG Junzheng. Path plan of 6-DOF robot manipulators in obstacle environment based on navigation potential function[J]. Transactions of Beijing Institute of Technology, 2015, 35(2): 186-191. |
| [9] |
王俊龙, 张国良, 羊帆, 等. 改进人工势场法的机械臂避障路径规划[J].
计算机工程与应用, 2013, 49(21): 266-270.
WANG Junlong, ZHANG Guoliang, YANG Fan. Improved artificial field method on obstacle avoidance path planning for manipulator[J]. Computer Engineering and Applications, 2013, 49(21): 266-270. DOI: 10.3778/j.issn.1002-8331.1201-0360. |
| [10] |
姬伟, 程风仪, 赵德安, 等. 基于改进人工势场的苹果采摘机器人机械手避障方法[J].
农业机械学报, 2013, 44(11): 253-259.
JI Wei, CHENG Fengyi, ZHAO De′an. Obstacle avoidance method of apple harvesting robot manipulator[J]. Transactions of The Chinese Society of Agricultural Machinery, 2013, 44(11): 253-259. DOI: 10.6041/j.issn.1000-1298.2013.11.043. |
| [11] |
孙绍杰, 齐晓慧, 苏立军, 等. 基于人工势场—遗传算法的机械臂避障方法研究[J].
计算机测量与控制, 2011, 19(12): 3078-3081.
SUN Shaojie, QI Xiaohui, SU Lijun. Obstacle avoiding research on artificial potential field the machine arm of robot based on method and genetic algorithm[J]. Computer Measurement & Control, 2011, 19(12): 3078-3081. |
| [12] |
杨强. Youbot机器人轨迹规划研究[D]. 广州: 广东工业大学, 2015.
YANG Qiang. Study on trajectory planning for Youbot robot[D]. Guangzhou: Guangdong University of Technology, 2015. |
| [13] | KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. International Journal of Robotics Research, 1985, 1(5): 500-505. |
| [14] | LAVALLE S M. Rapidly-exploring random trees: a new tool for path planning[J]. Algorithmic & Computational Robotics New Directions, 1999, 1(1): 293-308. |
| [15] |
李威洲. 基于RRT的复杂环境下机器人路径规划[D]. 哈尔滨: 哈尔滨工程大学, 2012.
LI Weizhou. Robot motion planning based on rapid-exploring random trees in complex environment[D]. Harbin: Harbin Engineering University, 2012. |
 2017, Vol. 20
2017, Vol. 20