制造业是国民经济的支柱产业。根据中国制造2025,制造企业需向质量效益竞争优势及绿色制造转变,而完成上述两个转变的基础之一是实现合理的车间调度。有效的调度优化方法可以使作业车间的各种生产制造资源得到充分利用,保证生产秩序的正常进行,并把在制品和流动资金减少到最低限度。因此做好生产调度工作是制造企业提升其竞争力的重要技术手段。
随着科学技术的发展,制造过程自动化水平不断提升,机器人在制造业的应用也日益广泛。如汽车制造行业、家电制造行业、零配件生产企业等,都不同程度地使用机器人来代替手工操作。但是一些复杂的、高精度的工作仍需工人的操作,因此目前生产现场中主要的资源包括机器设备、操作人员和机器人,其调度问题也可归属于多资源调度。
国内外学者一直注重多资源车间调度问题。刘志刚[1]和李鹏[2]针对设备、员工以及刀具等资源进行了多资源车间调度问题的研究,但是他们都没有考虑机器人在制造系统中的作用。孙志峻[3]和徐建国[4]考虑了设备、机器人和员工的多资源调度问题,但是文中考虑的机器人只是从事上料下料工作,没有考虑到机器人所具备的制造功能。
与以往作者仅将机器人当成上下料的辅助设备不同,本文认为,随着技术的发展,机器人在制造车间的作用远不止于此,机器人完全可以作为一种设备进行部分工序的操作。同时鉴于机器人具有上下料等辅助功能,零件在机器人上操作不需要员工的辅助;而在其他一般的设备上操作,则需要员工的辅助配合。因此文本将设备和机器人均看成能承担一定工序操作任务的资源,进行资源任务的合理分配,以满足零件的交货期、设备和机器人运作成本以及员工成本最低的要求。
1 问题的描述及数学模型的构建本文提出的多资源约束下的调度问题认为:制造系统中包括 M种不同的设备、 J种不同功能的机器人及 H个多技能员工来生产 P种不同的零件。每个零件的每道工序需要设备或机器人进行操作。考虑设备的上下料及其他辅助工序,本文认为零件工序在设备操作时需要人员的辅助操作,但员工完成某个零件工序的任务后,可直接转向下一个零件工序的操作,而零件由机器人操作的时候则不需要配备辅助的员工。问题的优化目标是:1)零件需要在交货时间窗内完成所有加工工序;2)尽可能使用较少的设备、机器人和员工,以降低制造过程中的运作成本和员工的工资成本。
1.1 模型假设及变量设定为了更好地描述多资源车间调度问题模型,本文提出的数学模型基于以下假设:
1) 零件加工工艺顺序为已知;
2) 零件在设备和机器人上的加工时间、交货时间等基本信息是已知的;
3) 每台机器加工零件都是非中断非抢占式的;
4) 每种设备和机器人均可以有多台;
5) 员工操作设备的基本信息已知;
6) 每个零件的不同工序可以由设备或者机器人中的某一个资源进行操作;
7) 员工在不同设备间的移动时间忽略不计;
8) 不考虑设备的故障问题。
符号及参数:
p为零件,
p=1, 2,…,
P,其中,
P表示零件的总数;
o为工序,
o=1, 2,…,
O
p
,其中,
O
p
表示零件
p的总工序;
m为设备,
m=1, 2,…,
M,其中,
M表示设备的种类数;
d
m
为第
m种设备的第
d台,
d
m
=1, 2,…,
N
m
,其中,
N
m
表示第
m种设备的总台数;
j为机器人,
j=1, 2,…,
J,其中,
J表示机器人的种类数;
e
j
为第
j种机器人的第
e台,
e
j
=1, 2,…,
W
j
,其中,
W
j
表示第
j种机器人的总台数;
h为工人,
h=1, 2,…,
H,其中,
H表示工人总数;[
a
p, b
p
]为零件
p的交货时间窗;
g
1
pom
=1为零件
p的工序
o需要在第
m种设备上加工;
g
2
poj
=1为零件
p的工序
o需要在第
j种机器人上加工;
Q
1
m
为需要第
m种设备进行加工的零件工序集合;
Q
2
j
为需要第
j种机器人进行加工的零件工序集合;
变量:
目标函数:
| $\quad\quad \min w = {Z_1} + {Z_2} + {Z_3},$ | (1) |
其中,
| $\quad\quad {Z_1} = \sum\limits_{p = 1}^P {\left( {\max (0,F_p - b_p) + \max (0,a_p - F_p)} \right)} C_1,$ | (2) |
| $\quad\quad {Z_2} = \sum\limits_{m = 1}^M {\sum\limits_{d_m = 1}^{N_m} {x_{m{d_m}}C_m} + \sum\limits_{j = 1}^J {\sum\limits_{e_j = 1}^{W_j} {y_{je_j}}C_j} } ,$ | (3) |
| $\quad\quad {Z_3} = \sum\limits_{h = 1}^H {z_hC_h}\text{。}$ | (4) |
其中, Z 1为零件完工时间不在时间窗内的惩罚成本; Z 2为设备及机器人的运作成本;Z 3为工人的工资成本。
约束条件:
| $\quad\quad \sum\limits_{d_m = 1}^{N_m} {x_{pom{d_m}} = 1} , \left( {p,o} \right) \in {Q_{1m}}, m = 1,2,..., M; $ | (5) |
| $ \quad\quad \sum\limits_{h = 1}^H {z_{poh} = 1} ,\left( {p,o} \right) \in {Q_{1m}},m = 1,2,...,M;$ | (6) |
| $ \quad\quad \sum\limits_{e_j = 1}^{W_j} {y_{poj{e_j}} = 1} ,\left( {p,o} \right) \in {Q_{2j}}, j = 1,2,...,J;$ | (7) |
| $\begin{array}{*{20}{l}}\displaystyle\sum\limits_{j' = 1}^J {{g_{2p \left( {o + 1} \right)j'}}} \times \sum\limits_{ej' = 1}^{W_j'} {y_{p\left( {o + 1} \right)j'{e_ j'}}}S_{p\left( {o + 1} \right)j'{e_j'}} + \\\displaystyle\sum\limits_{m' = 1}^M {{g_{1p\left( {o + 1} \right)m'} }} \times \sum\limits_{d_{m'} = 1}^{N_{m'}} {x_{p\left( {o + 1} \right)m'{d_m'}}S_{p\left( {o + 1} \right)m'd_{m'}}}{\text{≥}} \\ \displaystyle\sum\limits_{j = 1}^J {{g_{2poj}}} \times \sum\limits_{e_j = 1}^{W_j} {y_{poje jfpoje_j}} + \sum\limits_{m = 1}^M {{g_{1pom}}} \times \\\displaystyle\sum\limits_{d_m = 1}^{N_m} {x_{pomd_m}}{f_{pomd_m}} ,\forall p,o = 1,2,...,O_{p - 1};\,\,\,\,\quad\quad\quad\quad\quad\quad \end{array}$ | (8) |
| $\begin{split}& \displaystyle\sum\limits_{j = 1}^J {{g_{2poj}}} \times \sum\limits_{e_j = 1}^{W_j} {y_{poje_ j}}f_{poje_j} + \sum\limits_{m = 1}^M {{g_{1pom}}} \times \\& \sum\limits_{d_m = 1}^{N_m} {x_{pomd_m}}f_{pomd_m} = \sum\limits_{j = 1}^J {g_{2poj}} \times \\& (\displaystyle\sum\limits_{e_j = 1}^{W_j} {y_{poje_j}} S_{poje_j} + t_{poj}) + \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\& {\displaystyle\sum\limits_{m = 1}^M {{g_{1pom}}} \times \sum\limits_{dm = 1}^{Nm} {x_{pom{d_m}} \times } }\\& {\left[ {S_{pomd_m} + t_{pom} + \displaystyle\sum\limits_{h = 1}^H {(t_{poh} + r_{poh})z_{poh}} } \right]}; \forall p,o\;\text{;}\end{split}$ | (9) |
| $\begin{split}& {F_p = \displaystyle\sum\limits_{j = 1}^J {g_{2popj}} \times (\sum\limits_{e_j = 1}^{W_j} {y_{popje_j}} S_{popje_j} + t_{pop_j}) + }\\& \displaystyle\sum\limits_{m = 1}^M {{g_{1pop_m}}} \times \sum\limits_{d_m = 1}^{N_m} {x_{popmd_m} \times } \\& \left[ {S_{popmd_m} + t_{pop_m} + \displaystyle\sum\limits_{h = 1}^H {(t_{pop_h} + r_{pop_h}) \times z_{pop_h}} } \right]; \forall p ; \end{split}$ | (10) |
| $\begin{split}\\[-2pt]& x_{p'o'md_m}S_{p'o'md_m} + B(1 - {u_{1pop'o'md_m}}) {\text{≥}} \\& f_{pomd_m}x_{pomd_m}(p,o),(p',o') \in Q_{1m},\forall m,d_m\\& x_{pomd_m}S_{pomd_m} + B_{u1pop'o'md_m} {\text{≥}} \\& f_{p'o'md_m}x_{p'o'md_m};\end{split}$ | (11) |
| $\begin{split}\\[-2pt] & y_{p'o'je_j}S_{p'o'je_j} + B(1 - u_{2pop'o'je_j)} {\text{≥}} \\ & f_{poje_j}y_{poje_j}(p,o),(p',o') \in {Q_2}j,\forall j,e_j\\ & {y_{poje_j}S_{poje_j} \!+\! B_{u2pop'o'_je_j}\! {\text{≥}}\! f_{p'o'je_j}y_{p'o'je_j}};\end{split}$ | (12) |
| $\begin{split}\\[-2pt]& r_{p'o'h} + B(1 - u_{3pop'o'h}) {\text{≥}} \\& r_{poh} + t_{poh}(p,o),(p',o') \in {Q_{1m}},\forall m,h; \\& {r_{poh} + B_{u3pop'o'h} {\text{≥}} r_{p'o'h} + t_{p'o'h}}\text{;}\end{split}$ | (13) |
| $\quad\quad\sum\limits_{p = 1}^P {\sum\limits_{o = 1}^{O_p} {z_{poh}} } {\text{≤}} Bz_h , \forall h; $ | (14) |
| $\quad\quad\sum\limits_{p = 1}^P {\sum\limits_{o = 1}^{O_p} {x_{pomd_m} {\text{≤}} } } Bx_{md_m} , \forall m,d_m \text{;} $ | (15) |
| $\quad\quad\sum\limits_{p = 1}^P {\sum\limits_{o = 1}^{O_p} {y_{poje_j} {\text{≤}} } } By_{je_j}, \forall j,e_j\text{;}$ | (16) |
| $\quad\quad x_{pomd_m},y_{poje_j},z_{poh},z_p ,y{_{j_{{e_j}}}},{x_{m{d_m}}}= 0\; {\rm{or}}\;1\text{。}$ | (17) |
上述模型中式(1)~(4)表示目标函数,期望获得零件在非交货期窗口交货的惩罚成本、设备和机器人的运作成本、操作人员工资成本之和为最小。
式(5)~(17)表示约束条件。其中,式(5)表示如果零件 p的工序 o需要在第 m种设备上操作,则必须选择其中一台设备对其进行操作;式(6)表示如果零件 p的工序 o需要在设备操作,则必须选择一个员工进行辅助操作;式(7)表示如果零件 p的工序 o需要第 j种机器人上操作,则必须选择其中一台机器人对其进行操作;式(8)表示每个零件后一个工序开始的时间必须大于等于前一工序的完工时间;式(9)表示每个零件工序结束的时间等于该工序开始的时间加上操作时间;式(10)表示零件的完工时间;式(11)~(13)表示同一台设备、机器人或者员工在同一时刻只能操作一种产品;式(14)~(16)表示变量之间的逻辑关系;式(17)表示所有变量均为0-1变量。
2 基于遗传算法的模型求解遗传算法(genetic algorithm)是一类借鉴生物界进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法。它由Holland在1975年首先提出,目前已被广泛应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域[5]。Zhang[6],Nilsen[7],刘晓冰[8],邹攀[9]等都采用遗传算法或混合遗传算法求解车间调度模型,并证明了该方法具有较好收敛性和求解效果。
针对上述提出模型的复杂性,本节采用遗传算法进行问题的求解,同时采用自适应以及精英选择策略。
为了更好地说明如何应用改进遗传算法对模型进行求解,本节首先提出一个简单的算例。假设有5个零件,其工序顺序以及所需设备、机器人以及工人的情况如 表1和 表2。
| 表 1 零件操作工序与设备或机器人关系一览表 1) Tab. 1 The relationship between part processes and machines and robots |
| 表 2 员工与设备操作关系一览表 1) Tab. 2 The relationship between workers and machines |
编码
根据上述模型特征,在进行染色体编码时,考虑采用3层染色体编码。其中,第1层染色体主要是确定零件的操作顺序,第2层染色体用来确定员工的任务分配,第3层染色体主要考虑多台设备或机器人的具体分配。而染色体个体的长度则为
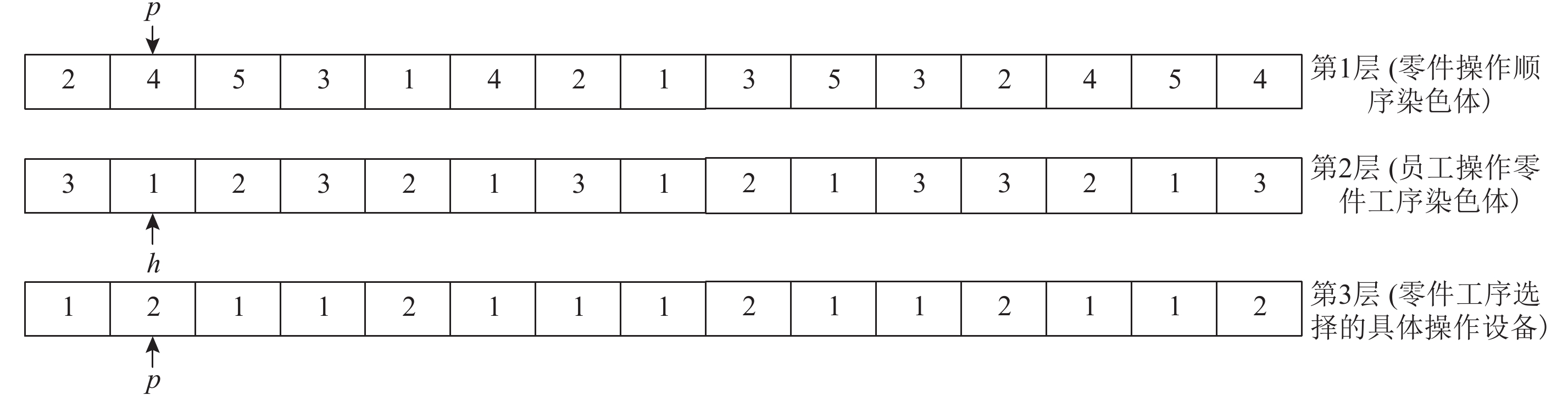
|
图 1 染色体编码 Fig. 1 The encoding of chromosome |
第1层中的2-4-5-3-1-4-2-1-3-5-3-2-4-5-4表示零件在设备或机器人上的排序,数字表示为具体的零件,而数字出现的次数则表示零件的工序。第2层和第3层的人员和具体某台设备或机器人的分配则与对应了1层的零件工序。如第2层表示零件工序操作所需的员工, 图1中第2层 h箭头指向的数字为1,则表示零件 P 4的第1道工序由第1个员工进行操作。如果该工序是由机器人操作的,可以设定该工人操作此工序的时间为0,从而符合调度模型的基本假定。而第3层的数字1,或者2则表示零件工序选择某种设备的具体在某一台设备上操作,如 图1第3层中 p所指的数据2表示零件 P 4的第1道工序在 J 3的第2台上操作。
目标函数的调整
在遗传算法中,为了方便父代的选择一般要求目标函数求极大化,因此需要对本数学模型中的目标函数进行调整,具体可见式(18)。在式(18)中考虑到 w的倒数可能非常接近于0,很难分辨不同适应度值得好坏,所以在倒数的基础上乘以10 b ,在求解中可以根据实际所得的数字来确定 b的值,从而增加不同适应度值差异范围。
| $ \quad\quad w' = {10^b}/w,\;b {\text{≥}} 0{\text{。}}$ | (18) |
遗传算子的设计
在遗传算法中通过选择、交叉和变异这3个步骤对染色体个体进行不断的优化,本文在此主要应用精英策略和自适应的方法对遗传算法进行改进。
选择
本文采用精英保留策略和轮盘赌相结合的方式选择进入交配池的父代个体。计算父代种群所有个体的适应度值,保留适应度最优的5%的个体直接进入下一代,而剩下的95%的个体通过对父代个体进行轮盘赌选择进行交配。
交叉
考虑到对第3层零件工序具体设备交叉时可能会出现不可行解的情况,本文仅对第1层和第2层采用两点交叉的方法进行交叉操作。在染色体个体中任意地选择2点,然后进行前后两端位置的交换。具体见 图2所示。
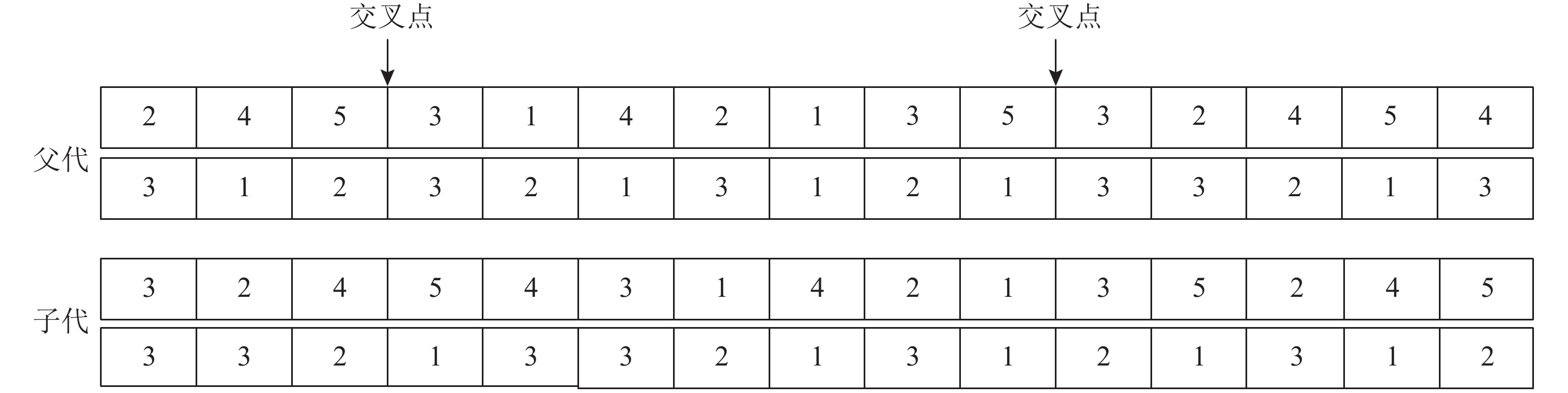
|
图 2 染色体交叉过程 Fig. 2 The crossover of chromosome |
变异
为了保证变异后仍然为可行解,本文第1层、第2层采用两点交换位置的方法进行变异,而对于第3层染色体则在确定变异点后,采用随机设定的方法进行。具体可见 图3所示。
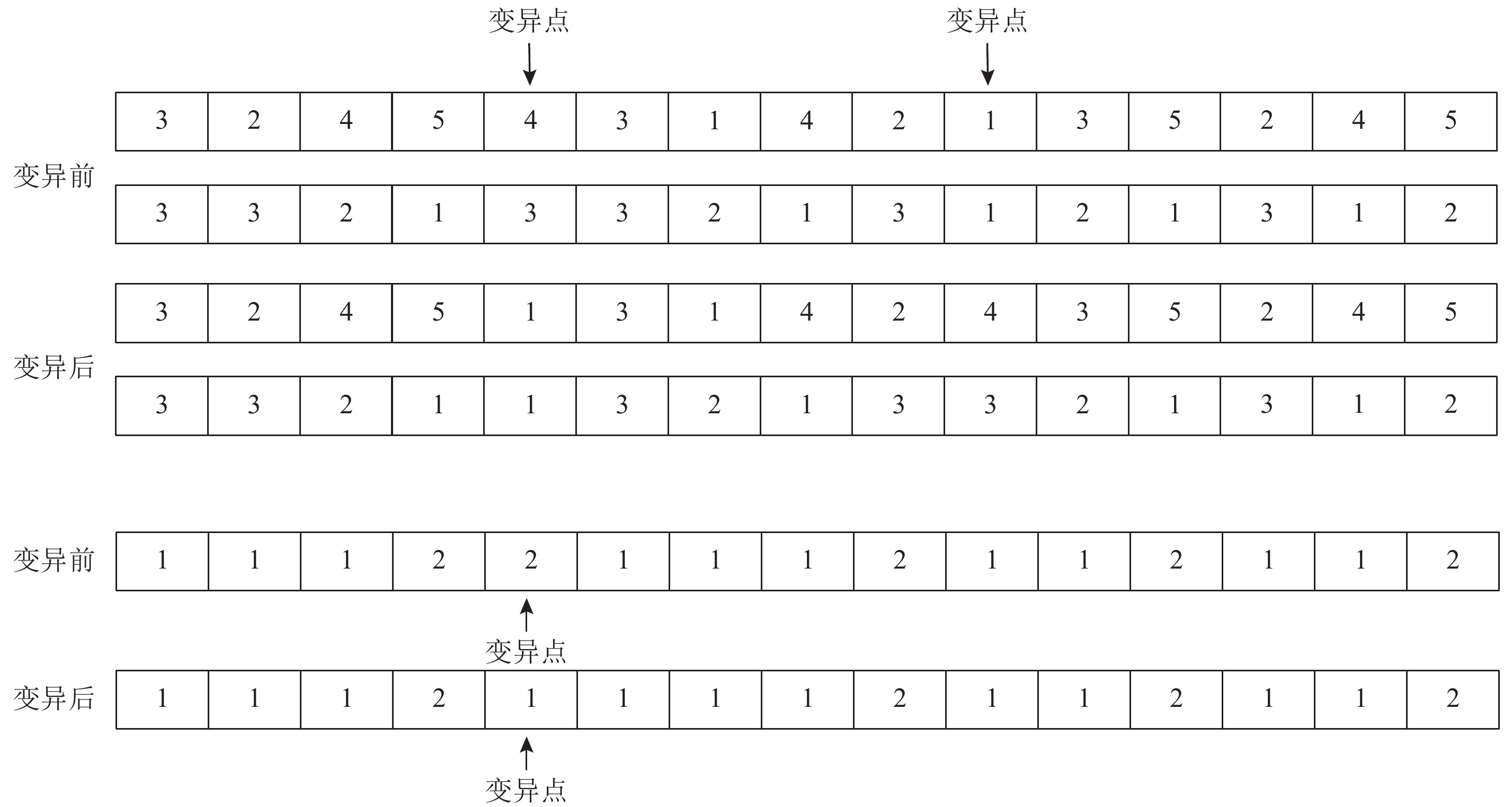
|
图 3 染色体变异过程 Fig. 3 The mutation of chromosome |
为了能够更好地对算法进行收敛和处理,本文采用自适应的交叉和变异。交叉算子和遗传算子会随着个体适应度值自动改变。交叉概率 P c 和变异概率 P m 按照以下公式自适应调整。
| $\begin{array}{l}\\[6pt]P_c = \left\{ \begin{array}{l}P_{c1} - \displaystyle\frac{{(P_{c1} - P_{c2})(f' - f_{{\rm{avg}}})}}{{f_{\max} - f_{{\rm{avg}}}}},f' {\text{≥}}f_{{\rm{avg}}};\\P_{c1},f' {\text{≤}} f_{{\rm{avg}}}\text{。}\end{array} \right.\\[20pt]P_m = \left\{ \begin{array}{l}P_{m1} - \displaystyle\frac{{(P_{m1} - P_{m2})(f_{\max} - f)}}{{f_{\max} - f_{{{\rm{avg}}}}}},f {\text{≥}} f_{{\rm{avg}}};\\P_{m1},f {\text{≤}} f_{{{\rm{avg}}}} \text{。}\end{array} \right.\end{array}$ | (19) |
其中, f max是指群体中最大适应度值; f avg指每一代群体的平均适应度值; f ′值为交叉染色体适应度值的较大值; f是指要变异个体的适应度值; P c1 =0.9; P c2 =0.6; P m1 =0.01; P m2 =0.001。
算法终止
本文采用当运算达到最大迭代次数,或最优个体的适应度值在一定循环周期内不再上升,或者最优个体已达到给定的阈值时,算法终止。
算法具体流程:
Begin
种群初始化;
While k≤maxgeneration(最大迭代次数)
按式(17)计算种群个体适应度值;
生成精英集合 N elite;
采用轮盘赌法,从 N- N elite中选择父代染色体;
根据式(18)计算交叉率和变异率;
交叉操作;
变异操作;
k= k+1;
End
End
3 算例分析由于上述提出的模型与前人的研究具有一定的差异,没有相类似的标杆数据进行对比分析,故本文应用上述模型和算法对7个不同规模的问题进行求解,具体可见 表3所示。
| 表 3 算例相关数据 1) Tab. 3 The relation data of example |
为了更好地说明模型以及求解的结果,本文以算例2为例,说明不同资源对整个调度的影响。算例2相关信息可见 表1和 表2,另外设定所有零件的交货时间窗均为[40, 100],应用以上模型求解算法得到零件加工顺序为4-2-3-5-1-5-2-3-2-4-3-5-4-1-4。而所需的员工分别为 H 1操作一台 M 1和一台 M 2, H 2操作一台 M 3,而机器人则不需要人工操作。 表4和 表5分别为零件工序选择的设备和零件工序开始(结束)时间。 图4 为该算例最后各零件工序加工的甘特图。
| 表 4 零件各工序所需设备 1) Tab. 4 The machines needed by part process |
| 表 5 零件各工序开始(结束)时间 Tab. 5 The start (finish) time of each part process |
设备 M 2和 J 3各有2台。从 图4可以看出,对于设备 J 3,第1台加工了 P 4的第1道工序,第2台加工了 P 2的第2道工序和 P 5的第3道工序,这样的安排使得零件的加工周期为95;如果仅用到一台 J 3,会使得整个加工周期延长至105。而对于设备 M 2,最终却仅选用了一台进行操作,因为不管使用1台设备还是2台设备整个加工周期都不会发生变化。同时在操作人员安排上, H 1一人操作2台设备,从而导致 H 1必须在操作完 P 3的第3道工序后才能操作 P 4的第3道工序,从而使得 P 4的第3道工序加工时间推迟了3 min,进而使得整个加工周期推迟了3 min。但是如果让 H 3操作 P 4的第3道工序,则整个加工周期可以缩短3 min,但是由于这3 min并不影响零件的交货的时间要求,故最终只选择2个工人进行设备的操作,从而满足目标函数中总成本最低的要求。
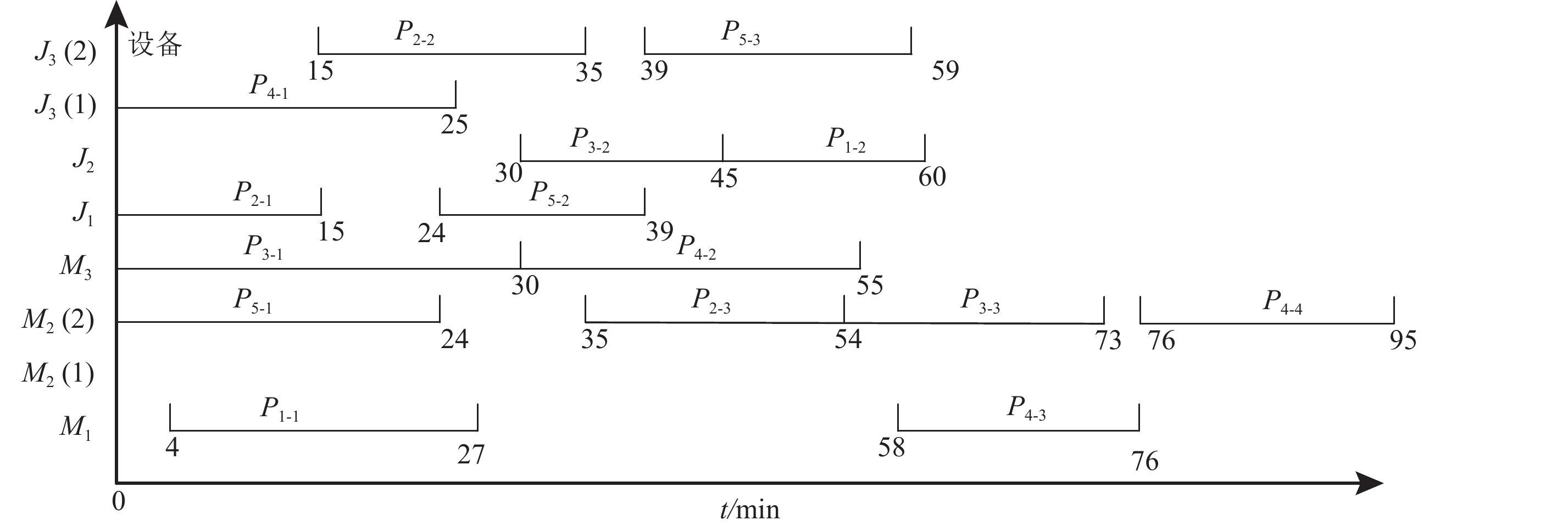
|
图 4 算例2零件加工甘特图 Fig. 4 The Gantt chart of the result for the Example 2 |
随着科学技术的不断提高,机器人在制造企业中的作用越来越大,使得原来的单资源、双资源调度问题晋身为了现在的多资源调度问题。本文在详细介绍多资源调度问题的现状后,提出了设备、人员以及机器人的多资源调度问题的数学模型,并采用了改进遗传算法对模型进行了求解验证。
在研究内容上,考虑到问题的复杂性,本文假设每种零件只有一条加工工艺路径,这在一定程度上限制了模型在实际问题中的应用范围。因此在后续研究中,将进一步研究多工艺路径及员工流动环境下的多资源调度问题。
在研究方法上,由于模型变量设置相对比较简单,本文采用遗传算法进行了求解,在速度和最优解方面都获得较好的效果。当模型复杂程度不断提升后,将进一步研究更有效的混合算法对模型的求解,提高算法的效率。
| [1] |
刘志刚, 李言, 李淑娟. 基于蚁群算法的Job-Shop多资源约束车间作业调度[J].
系统仿真学报, 2007, 19(1): 216-220.
LIU Zhigang, LI Yan, LI Juanshu. Multi-resource constrained job-shop optimization scheduling based on ant colony algorithm[J]. Journal of System Simulation, 2007, 19(1): 216-220. |
| [2] |
李鹏, 邱顺流, 宋豫川, 等. 基于瓶颈工序的多资源多目标机械加工车间调度研究[J].
现代制造工程, 2013, 1: 1-6.
LI Peng, QIU Shunliu, SONG Yuchuan. Research on multiple resources constrained and multi-objective machining job shop scheduling based on bottleneck operations[J]. Modern Manufacturing Engineering, 2013, 1: 1-6. DOI: 10.3969/j.issn.1671-3133.2013.01.002. |
| [3] |
孙志峻, 朱剑英, 潘全科. 基于遗传算法的多资源作业车间的智能动态优化调度[J].
中国机械工程, 2002, 38(4): 120-123.
SUN Zhijun, ZHU Jianying, PAN Quanke. Genetic algorithm based approach to the intelligent optimum scheduling of multi-resources in the dynamic environment[J]. Chinese Journal of Mechanical Engineering, 2002, 38(4): 120-123. |
| [4] |
徐建国. 多资源生产调度问题的分析建模[D]. 安微: 合肥工业大学, 2008.
XU Jianguo. Modeling of multi-resource production scheduling problem [D]. Anhui: Hefei University of Technolgoy, 2008. |
| [5] | 玄光男, 程润伟. 遗传算法与工程优化/应用数学译丛[M]. 于歆杰, 周根贵译. 北京: 清华大学出版社, 2004. |
| [6] | Zhang Q, Manier H, Manier M A. A genetic algorithm with tabu search procedure for flexible job shop scheduling with transportation constraints and bounded processing times[J]. Computers and Operations Research, 2012, 39: 1713-1723. DOI: 10.1016/j.cor.2011.10.007. |
| [7] | KUNDAKCI N, KULAK O. Hybrid genetic algorithms for minimizing makespan in dynamic job shop scheduling problem[J]. Computers & Industrial Engineering, 2016, 96(6): 31-51. |
| [8] |
刘晓冰, 焦璇, 宁涛, 梁旭, 等. 基于双链量子遗传算法的柔性作业车间调度[J].
计算机集成制造系统, 2015, 21(2): 495-502.
LIU Xiaobing, JIAO Xuan, NING Tao, LIANG Xu. Flexible job shop scheduling based on double chains quantum genetic algorithm[J]. Computer Integrated Manufacturing Systems, 2015, 21(2): 495-502. |
| [9] |
邹攀, 李蓓智, 杨建国, 施烁, 等. 基于分层蚁群遗传算法的多目标柔性作业车间调度方法[J].
中国机械工程, 2015, 26(21): 2873-2880.
ZOU Pan, LI Beizhi, YANG Jianguo, SHI Shuo. Hierarchical ant-genetic algorithm-based multi-objective intelligent approach for flexible job shop scheduling[J]. Chinese Journal of Mechanical Engineering, 2015, 26(21): 2873-2880. DOI: 10.3969/j.issn.1004-132X.2015.21.006. |
 2017, Vol. 20
2017, Vol. 20