随着物流领域的迅速发展和生活水平的不断提高，冷链物流也得到快速的发展。冷链物流是指在冷藏环境下保证食品质量，减少食品损耗，以冷冻工艺学为基础、以制冷技术为手段，进行冷藏类食品的物流过程^[1]。冷藏类食品具有易腐烂、易变质等特性，在流通过程中需要持续保持适宜的温度，并需要较快的周转速度。因此在冷链物流的整个环节都必须配备合适的设备来加强管理，以保证冷藏品的质量。鉴于冷链物流的特殊性质，冷链物流配送路径优化问题可以归结为带有时间窗的车辆路径问题(vehicle routing problems with time windows, VRPTW)，它是在经典车辆路径问题(vehicle routing problems, VRP)的基础上加上了时间窗限制、车容量限制等约束条件^{[2- 4]}。目前，用于求解此类车辆路径问题的方法较多，经典的方法有割平面法、分支定界法、动态规划方法等。由于该问题的可行解都是一个NP难题(非多项式算法难题)，因此，一些启发式算法不断地在求解中应用，如粒子群算法^[5]、遗传算法^{[6- 7]}、蚁群算法^[8]、禁忌搜索算法^[9]等智能优化算法。这样一来，大量的VRP问题在应用方面很好地得到了解决。

虽然启发式算法已经大规模运用到冷链物流配送路径优化研究中，也取得了较大的研究成果。但是由于一些启发式算法存在收敛速度慢、搜索成功率较低等缺陷，因此为了克服这种情况，本文在前人研究的基础之上，把智能水滴算法应用到冷链物流配送路径优化问题中。智能水滴(intelligent water drop, IWD)算法是2007 年由Shah-Hosseini^[10]提出来的，它通过模仿自然界水系统中水滴群与其周围环境作用而形成河流的过程，不断进行迭代运算，最后得到优化的结果。智能水滴算法提供了一种新的解决方案来处理NP难题。

1 冷链物流配送路径优化模型的建立

冷链物流配送路径优化问题属于带时间窗的车辆路径问题。基于此种情况，冷链物流配送路径问题可作如下描述：一个冷链物流中心(用 O表示)，使用 K辆冷藏车在规定时间内向 N个需求地(一般为超市)送货，在满足各需求地货物需求量、运输车辆容量限制等约束条件下，要求车辆综合配送成本最低。已知每个需求地 i的需求量为 q _i ，该需求地服务时间及其时间窗限制 $\left[ {{e_i},{l_i}} \right]$ ，其中 e _i 为最早开始服务时间， l _i 为最晚开始服务时间。定义如下。

d _ij 为需求地 i到需求地 j之间的距离( i、 j=1, 2，…， N)。

Q _k 为车辆 k的最大载重量。

D _k 为车辆 k最大行驶距离。

m _k 表示车辆 k参与配送的需求地总数，若车辆 k没有参与配送，记 m _k =0。

t _ij 表示车辆从需求地 i到需求地 j开展配送的运输时间。

u _ik 表示车辆 k为第 i个需求点提供服务(装卸货物)所需要的时间。

h _i 为车辆到达第 i 个需求点的时间。

q _i 为客户 i的货物需求量。

c为车辆的单位距离运输成本。

c ₁为车辆未按某需求地规定时间而提前到达该处的等待成本。

c ₂为车辆在某一需求点的最晚要求时间之后到达该处的处罚成本。

ω _k 为每部车辆运营时所需负担的固定成本。

$\begin{array}{l}x_{ij}^k = \left\{ \begin{array}{l}1,\;\;\;{\text{车辆}}k{\text{从第}}i{\text{个需求点直接到达第}}j{\text{个需求点}};\\0,\;\;\;{\text{否则}} \text{。}\end{array} \right.\\[10pt]y_i^k = \left\{ \begin{array}{l}1,\;\;\;{\text{需求点}}i{\text{由车辆}}k{\text{配送}};\\0,\;\;\;{\text{否则}} \text{。}\end{array} \right.\end{array}$

p为配送冷藏品的单位成本。

μ ₁为运送过程中冷藏品损坏量占总量的损比值。

μ ₂为装卸搬运操作过程中损坏量占总量的损比值。

基于综合最低配送成本的带时间窗的冷链物流配送路径问题数学模型如下：

$\quad\quad \min\; C = \min\; ({{\rm{C}}_1} + {C_2} + {C_3} + {C_4}) \text{。}$

其中， ${C_1} = \displaystyle\sum\limits_{k = 1}^K {\sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {cx_{ij}^k{d_{ij}}} } } $ ，为配送车辆的运输成本；

${C_2} = \displaystyle\sum\limits_{k = 1}^K {{\omega _k}} $ ，为配送车辆的固定成本；

${C_3} = {c_1}\displaystyle\sum\limits_{i = 1}^N {\max\; ({e_i} - {h_i},0)} + {c_2}\sum\limits_{i = 1}^N {\max\; ({h_i} - {l_i},0)} $ ，为客户惩罚成本；

${C_{\rm{4}}} = p \displaystyle\sum\limits_{k = 1}^K {\sum\limits_{i = {\rm{0}}}^N {y_i^k\left( {{\mu _1}{t_{ij}} + {\mu _2}{q_i}} \right)} } $ ，为冷藏品的货物损坏成本。

约束条件如下。

1) $\displaystyle\sum\limits_{i = 1}^{{m_k}} {{q_i}y_i^k} {\text{≤}} {Q_k}$ ，表示车辆装载量能够满足该条线路上各需求地的总需求量。

2) $\displaystyle\sum\limits_{k = 1}^K {\sum\limits_{j = 1}^N {x_{oj}^k} } = K$ ，表示配送中心为起始出发点，每辆车都必须从此处出发。

3) $\displaystyle\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {x_{ij}^k{d_{ij}}} } {\text{≤}} {D_k}$ ，表示每辆车的行驶距离受该车最大行驶距离的限制。

4) $\displaystyle\sum\limits_{i = 1}^N {\sum\limits_{k = 1}^K {{y_{ik}}} } = 1$ ，表示每个需求点有且只有一辆车为其提供服务。

5) $\displaystyle\sum\limits_{k = 1}^K {{m_k}} = N$ ，表示所有需求地都需得到配送服务。

6) $x_{ij}^k = \left\{ \begin{array}{l}1, \text{车辆}k \text{从第}i \text{个需求点直接}\\\quad \text{到达第}j \text{个需求点；}\\0, \text{否则} \text{。}\end{array} \right.$

7) $y_i^k = \left\{ \begin{array}{l} 1,\;\;\;{\text{需求点}}i{\text{由}}k{\text{车辆配送}};\\ 0,\;\;\;{\text{否则}} \text{。} \end{array} \right.$

8) $\displaystyle\sum\limits_{j = 1}^N {x_{ij}^k} = y_i^k$ ，表示如果第 k辆车到达第 j个点，则必为第 j个需求点提供服务。

9) $\displaystyle\sum\limits_{j = 1}^N {x_{ij}^k} = y_j^k$ ，表示车辆 k为第 i个需求点提供服务，则完成服务后必须从该点离开。

10) ${e_i}{\text{≤}} {u_{ik}} {\text{≤}} {l_i}$ ，表示如果第 k辆车为第 i 个需求点提供服务，则必须在该点规定的时间窗内完成服务。

2 智能水滴算法 2.1 智能水滴算法的原理

在自然界当中，河流中流动的水滴组成了庞大的移动群体，水滴群由于受重力影响而向目的地流动。在现实情况中，由于受河流中障碍物的影响，水滴群并不能从水滴源头由理想直线路径流动到终点，水滴运动的实际路径大都与理想路径相差甚远^[11]。流动中的水滴主要具有两个属性。1)流动中的水滴具有一定的速度，从河床带走泥土的过程中，速度起了重要的作用，速度快的水滴够携带更多的泥土。2)流动的水滴可以从河床带走一定数量的泥土；随着水流的前进，水滴能够把泥土从一个位置携带到另一个位置，水滴中泥土数量在增加，河床中泥土数量在减少，而且水滴还会从运动的路径中带走一些泥土^[12]。除了上述两个主要属性外，自然界中水滴还有另一个属性：水滴在某一路径当中流动的难易程度由路径当中所含泥土量的多少来衡量；所含泥土量越少，水滴便会以更大的概率选择此条路径^[13]。水滴的这些属性与实际的物流配送存在共同之处，能作为解决物流配送的一种方法。

2.2 智能水滴算法的数学描述

根据分析水滴的属性可知，水滴运动时具有速度 v(IWD)，水滴运动时携带泥土量 s( i, j)。水滴在河道中流动时 v(IWD)和 s( i, j)会随时发生变化，直至找到最优路径到达目的地。由于实际的水流是连续的，在建立模型中把连续流动的水流看作离散运动^[11]。水滴从河道某一位置 i运动到另一位置 j的过程中的速度增量为∆ v(IWD)，该速度增量与位置 i， j之间的泥土量呈负相关，具体关系可表示如下：

$\quad\quad \Delta v({\rm{IWD}}) = \frac{{{a_v}}}{{{b_v} + {c_v}{s^\alpha }(i,j)}} \text{。}$

(1)

其中， a _v ， b _v ， c _v 以及 α均为实际运算中设置的参数。

水滴从位置 i运动到位置 j的过程中，水滴中泥土含量会增加，增加量为∆ s(IWD)，与此同时，该过程的河道位置 i， j之间的泥土减少量为∆ s( i, j)。一般而言，二者数量相等，即

$\quad\quad \Delta s({\rm{IWD}}) = \Delta s(i,j){\text{。}}$

(2)

河道位置 i， j之间的泥土减少量∆ s( i, j)与水滴从位置 i运动到位置 j的时间 t( i, j)呈负相关，具体关系可表示如下：

$\quad\quad \Delta s({\rm{IWD}}) = \frac{{{a_s}}}{{{b_s} + {c_s}{t^\beta }(i,j)}}{\text{。}}$

(3)

与上文一样， a _s ， b _s ， c _s 以及 β均为实际运算中设置的参数。

上述提到 t( i, j)为水滴位置 i运动到位置 j的时间，与位置 i至位置 j的距离呈正相关，具体关系可表示如下：

$\quad\quad t(i,j) = \frac{{d(i,j)}}{{v({\rm{IWD}})}}{\text{。}}$

(4)

当水滴从位置 i运动到位置 j后，该路径中泥土含量将被更新，局部更新计算公式为

$\quad\quad s(i,j) = (1 - \rho )s(i,j) - \rho \Delta s(i,j){\text{。}}$

(5)

其中， ρ为局部泥土更新量参数，且0＜ ρ＜1。

智能水滴中的泥土含量也会被更新，更新计算公式为

$\quad\quad s({\rm{IWD}}) = s({\rm{IWD}}) + \Delta s({\rm{IWD}}){\text{。}}$

(6)

前文介绍了智能水滴的一种属性，即在某一路径当中流动的难易程度是由路径中所含泥土量的多少来衡量的，所含泥土量越少，水滴便会以更大的概率选择此条路径。针对这一机制，以 P( i, j)表示智能水滴在位置 i选择 j作为下一位置的概率，它与路径( i, j)中的泥土含量呈负相关。选择下一位置的具体概率为

$\quad\quad P(i,j) = \frac{{f(s(i,j))}}{{\sum\limits_k {f(s(i,k))} }}{\text{。}}$

(7)

其中， f ( s ( i , j)) 是与位置 i至位置 j之间泥土含量相关的函数：

$\quad\quad f(s(i,j)) = \frac{1}{{\eta + g(s(i,j))}}{\text{。}}$

(8)

常量 η是极小的正数，通常取值为0.01，加入常量 η是为了防止函数 f的分母为0 。而加入函数 g(·)是为了确保位置 i 到位置 j 之间的路径泥土量为正数，具体表示为

$\quad\quad g(s(i,j)) = \left\{ \begin{array}{l}\!\!\!\!\!s(i,j),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\min \;s(i,j) {\text{≥}} {\rm{0;}}\\\!\!\!\!\!s(i,j) - \min \;s(i,j),\;\;\;{\text{否则}}。{\text{。}}\end{array} \right.$

(9)

当水滴群中所有的水滴从起点到达目的地之后，都会形成相应的路径，各个水滴运动形成的路径长度用 E _IWD表示，最优路径集合为 $\left\{ {E_{{\rm{IWD}}}^k} \right\}$ 。其中，最优路径为智能水滴从起点至目的地形成的最短路径。然后对最优路径进行迭代后可得出最优的路径解

$\quad\quad {E_{{\rm{IB}}}} = \min \left\{ {E_{{\rm{IWD}}}^k} \right\}{\text{。}}$

(10)

设当前最优路径为 E _TB，则 E _TB可按下述公式进行更新：

$\quad\quad {E_{{\rm{TB}}}} = \left\{ \begin{array}{l}\!\!\!\!\!{E_{{\rm{TB}}}}{\rm{,}}\;\;\;\;{E_{{\rm{TB}}}} {\text{＞}} {\rm{ }}{E_{{\rm{IB}}}};\\[5pt]\!\!\!\!\!{E_{{\rm{IB}}}},\;\;\;\;\;\;{\text{否则}}{\text{。}}\end{array} \right.$

(11)

针对每次智能水滴算法的迭代，当此次迭代结束后，根据以下更新公式对每一条最优的路径 E _IB进行全局泥土量更新：

$\quad\quad s(i,j) = (1 + {\rho _{\rm {_{IWD}}}})s(i,j) - {\rm {\rho _{_{IWD}}}} \cdot \frac{{s({\rm{IWD}})}}{{{N_{{\rm{IB}}}} - 1}}{\text{。}}$

(12)

2.3 智能水滴算法的改进

根据上述分析可知，智能水滴算法每次迭代结束后只会对最优解中的河流泥土量进行更新，如此一来将会影响该算法求解的数量，易导致算法陷入局部最优^[14]。针对该问题，本文在智能水滴算法当中加入了次优解集合理论和收缩因子。目的是既要对最优解中河流泥土量进行更新，还对次优解集合中的河流泥土含量进行更新，同时也为了避免过早收敛。设算法每次迭代中的最优解集合为 ${E_{{\rm{best}}}} = \left\{ {{E_1},\;} \right.$ $\left. {{E_2}, \cdots ,{E_i}, \cdots ,{E_n}} \right\}$ ，对其进行邻域扩展，得到邻域集合 $E_{{\rm{best}}}^H = \left\{ {E_1^ + ,\;E_1^ - , \cdots ,E_i^ + ,E_i^ - , \cdots ,E_n^ + ,E_n^ - } \right\}$ ，其中 ${E_i^ + }$ 和 ${E_i^ - }$ 分别为可行域中与 E _i 相邻的解。由此可知新的解的集合为 ${E^N} = E_{{\rm{best}}}^H \cup {E_{{\rm{best}}}}$ 。在每次迭代结束后，次优解集合中的任意2个客户点之间的泥土含量更新公式为

$\quad\quad s(i,j) = (1 + {\rm {\rho _{_{IWD}}}})s(i,j) -{\rm {\rho _{_{IWD}}}} \cdot \frac{{\theta s({\rm{IWD}})}}{{{N_{{\rm{IB}}}} - 1}}{\text{。}}$

(13)

其中， ρ _IWD 为智能水滴全局泥土更新量参数， θ为收缩因子， $\theta = \displaystyle\frac{{2\left( {1 - i/{\rm{ite}}{{\rm{r}}_{\max }}} \right)}}{{\left| {2 - \varphi - \sqrt {{\varphi ^2} - 4\varphi } } \right|}}$ ，其中 i为当前迭代数，iter _max为总迭代数， $\varphi $ 为智能水滴的加速常数，一般情况下 $\varphi $ ＞4，本文取 $\varphi $ =4.1。收缩因子能够大幅度更新路径之间的泥土含量，使得算法能快速搜索到最优解，而且还能有效避免算法陷入局部最优。

同时，因为水滴的移动会使某一路径中的泥土含量发生变化，当某段路径的泥土含量远多于其他路径的泥土含量时，就会导致智能水滴算法提早进入收敛状况^[15]。为避免此种情况，这里通过借助最大最小蚁群算法(MMAS)的设置上下限思想，对水滴群路径上的泥土量设置了最大和最小量的限制^[16]。对每条路径上的 s( i, j)，有 ${s_{\min }} {\text{≤}} s(i,j) {\text{≤}} {s_{\max }}$ 。如此一来，每次迭代完成后，确保泥土量的值还在这个范围内。当 $s(i,j) {\text{＞}} {s_{\max }}$ 时，则令 $s(i,j) = {s_{\max }}$ ，当 $s(i,j) {\text{＜}} {s_{\min }}$ ，则令 $s(i,j) = {s_{\min }}$ 。同时也要确保 ${s_{\min }} {\text{＞}} 0$ ，这样就能保证每条路径被选择的概率都不为0。

$\quad\quad {s_{\min }} {\text{≤}} s(i,j) {\text{≤}}{s_{\max }}{\text{。}}$

(14)

其中 s _max和 s _min的计算公式为

$\quad\quad {s_{\max }} = \frac{{1 + \rho }}{{2(1 - \rho )E({\rm{cur}})}} + \frac{{2(1 - \rho )}}{{E({\rm{cur}})}},$

(15)

$\quad\quad {s_{\min }} = \frac{{{s_{\max }}}}{{2n}}{\text{。}}$

(16)

ρ为局部泥土更新量参数； n为水滴能够到达目的地个数； E(cur)为当前最优解。

2.4 算法流程

1) 输入初始变量，例如 a _s ， b _s ， c _s ， β， a _v ， b _v ， c _v ， α。以及局部泥土更新量参数 ρ，智能水滴全局泥土更新量参数 ρ _IWD ，智能水滴个数 M，最大迭代次数iter _max，智能水滴初始泥土量 s _Init以及初始速度 v _Init等。

2) 由式(7)、(8)对智能水滴下一位置进行更新。

3) 由式(1)对智能水滴的速度进行更新。

4) 根据式(3)、(6)对各个智能水滴的泥土含量进行更新；并根据公式(5)、(14)~(16)对局部路径泥土含量进行更新。

5) 根据式(10)、(11)迭代出智能水滴路径局部最优解和全局最优解。假使当前最优路径没有到达全局最优路径水平，则进行第6)步工作；相反，则进行第7)步工作。

6) 根据式(13)更新智能水滴最优路径泥土含量。

7) 确定当前迭代次数与最大迭代次数关系，如果当前迭代次数小于最大迭代次数，则返回第一步继续进行迭代；相反，则终止此循环。

3 仿真实验与分析

某一冷链物流配送中心需要向该地区8家超市配送冷藏品，这项任务由配送中心发出的3辆容量为8t的冷藏车辆来完成配送，每个需求地的需求量、所需的服务时间以及所要求的时间窗如 表1所示；配送中心与各个需求地，以及各个需求地之间的距离如 表2所示。每辆冷藏车的平均行驶速度为40 km/h，则任意两点之间的行驶时间 ${t_{ij}} = \displaystyle\frac{{{d_{ij}}}}{{40}}$ ，物流中心的车辆为统一车辆，每km的平均运输成本为20元(主要体现在燃油、耗电以及车辆损耗上)；由于冷藏车均配有专门司机和卸货人员，每辆车运行的固定成本为30元；冷藏品的成本为10 000元/t；车辆运送过程中冷藏品损坏量占总量的损比值为0.1%；装卸搬运操作过程中损坏量占总量的损比值为0.2%；车辆提前到达某一需求点处的等待成本 c ₁，同时各需求点规定当车辆在某一需求点要求时间之后到达该处，则处罚成本 c ₂均按50元计算。

此类问题属于线性规划问题，运用线性规划方法最终求得的最优行驶成本路径为：

车辆1：配送中心 O→需求地8→需求地5→需求地7→配送中心 O；

车辆2：配送中心 O→需求地6→需求地4→配送中心 O；

车辆3：配送中心 O→需求地3→需求地1→需求地2→配送中心 O。

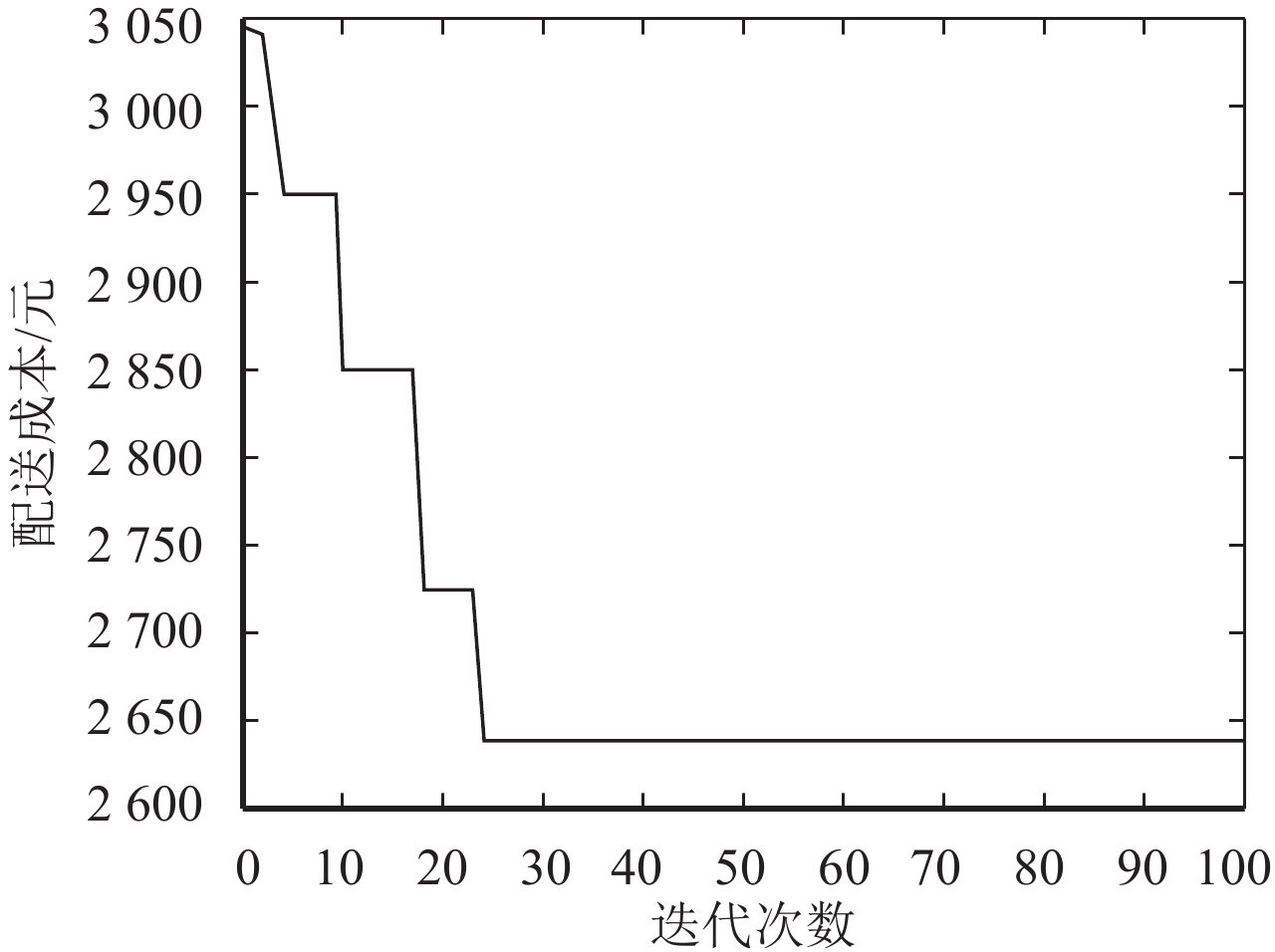
综合最低成本为2 638元。此类线性规划问题求解较为复杂，运算时间较长。基于此种情况，本文可采用改进后的智能水滴算法对其进行求解。智能水滴算法初始参数设置为： a _s ， b _s ， c _s 和 a _v ， b _v ， c _v 分别为1、0.1、1； α=1， β=1；局部泥土更新量参数 ρ=0.9，智能水滴全局泥土更新量参数 ρ _IWD =0.9，智能水滴个数 M=100，最大迭代次数iter _max=100，智能水滴初始泥土量 s _Init=10 000以及初始速度 v _Init=100。本文使用Matlab R2014a对算法进行仿真实验，仿真硬件环境为: 双核3.0 G CPU，2 G内存，硬盘为500 G；操作系统为windows7。在运行100次之后，有92次找到最优解，搜索到最优解的成功率为92%。其中最快需要迭代5次即可得到最优解，最慢需要迭代42次才能得到，平均迭代次数为16次。本文选取一个迭代24次搜索到最优解智能水滴，具体收敛过程如 图1所示。

为了体现本文方法的优越性，本文选取智能水滴算法、蚁群算法和遗传算法分别对此类问题进行求解，迭代次数均为100次。最终得到四者结果对比如 表3。

通过对比 表3中的数据可以发现，对于解决带有时间窗的冷链物流配送路径优化问题，本文提出的改进智能水滴算法，无论是在求解的平均值、搜索成功率还是平均迭代次数都要优于传统的智能水滴算法。不仅如此，本文提出的改进算法相比遗传算法和蚁群算法也有很大的优越性。

4 结论

本文建立的冷链物流配送综合运输成本最低模型，能够有效地反映出实际配送中的综合成本支出。同时，本文介绍了一种新型的智能算法——智能水滴算法，并在智能水滴算法基本原理基础上，对智能水滴算法进行了改进，把改进后的智能水滴算法应用到冷链物流配送综合运输成本最低模型中。最后通过仿真实验证明改进后的智能水滴算法能更加精确地求解此模型，该方法有效地避免了传统智能水滴算法易陷入局部最优和收敛速度过快等缺陷，相比其他智能算法有较强的优越性，是求解带时间窗的车辆路径问题的一种行之有效的方法。在下一步研究中，可以将改进的智能水滴算法运用到多车型、多配送中心等问题中去，从而丰富智能水滴的算法。