航空公司收益管理是指航空公司根据不同的乘客需求，将不同等级的机票以最合适的价格销售给最合适的乘客来获得最大的收益^[1]。机票作为一种典型的易逝品，其价值随着时间急剧流逝，因而航空公司机票价格往往是一个动态的过程。但正是由于不同时期机票价格不同，使得乘客的购买效用存在差异，理性的乘客会根据对机票价格的预期选择购买时机，这类乘客被称为“策略性乘客”^[2]。策略乘客这一选择购买时机的行为使得航空公司原有的价格体系受到极大的挑战^[3]。因此，如何在乘客具有策略行为下的情况下对机票实施动态定价并提出应对机制，对航空公司的收益管理具有一定的指导意义。

现有文献中研究应对顾客策略行为的机制大多假设在需求确定下，如彭志强^[4]研究了可退票机制、可召回机制、差价补偿和快速补货机制对消费者策略行为的缓解作用。Prasad等^[5]提出产品绑定和预留产品定价机制来缓解顾客的策略行为。而在需求不确定下考虑顾客策略行为的应对机制较少。Jerath等^[6]研究需求不确定下针对顾客的策略行为，提出了模糊销售机制，即当厂商存在剩余产品时，厂商可在销售后期引入中介机构，将剩余产品转移给中介销售。模糊销售实质上是一种促销机制。不同的是，这种销售机制可以隐藏产品的差异性，吸引更多顾客。关于模糊销售的文献有：Fay^[7]认为当一个行业品牌偏好较弱时，通过模糊销售会加大市场竞争，但减少了整个行业的利润。相反，当品牌偏好较大时，会减少市场竞争。Anderson和Xie^[8]认为通过模糊销售隐藏某种产品或服务的差异性，不但可以高价卖给老顾客，还可通过折扣价吸引更多新客户，从而增加企业的收益。虽然Jerath等^[6]在需求不确定下研究了模糊销售的可用性，但是该文没有考虑到顾客的策略程度，也没探讨模糊销售机制的可行性，在实践中缺乏一定的说服力。

本文在Jerath等^[6]的基础上，从乘客的购买行为出发，利用Hotelling模型建立航空公司和策略乘客的两周期动态博弈，引入中介进行模糊销售，探讨需求不确定下航空公司如何利用模糊销售实现收益最大化，并从航空公司和中介的视角分析模糊销售机制的有效性，对航空公司在需求不确定下的定价和收益管理具有一定的指导意义。

1 问题描述与假设

考虑如下问题：某一条航线上的航班分别由2个相互竞争的航空公司A、B提供，航空公司在有限的时间内销售 K张机票，假设每个航空公司分别持有 K/2张机票。飞机起飞后，剩余机票价值为零。假定航空公司A、B分别位于长度为1的Hotelling线的两端，乘客均匀分布在整条线上，且乘客具有策略行为，会根据当前的价格信息以及对未来机票来源和可得性的预期做出购买决定。线上任意一点乘客 x的购买偏好取决在Hotelling线上的位置，其中 x _A、 x _B分别表示从航空公司A、B购买机票，且是Hotelling线上离A、B公司最远的乘客的位置，位于 x _A左边的所有乘客从航空公司A购买机票，位于 x _B右边的乘客从航空公司B购买机票，如 图1所示。每位乘客限购一张机票，对机票的最大支付意愿为 V，为了便于分析，假定乘客对机票的估价相同。

本文将整个销售期分为2个周期，提出2种销售策略。一是传统销售，即航空公司通过自己的现有渠道进行销售。二是模糊销售，航空公司在周期1通过自己现有渠道销售，周期1结束后若还存在剩余机票，在周期2引入中介机构销售剩余机票，中介在售出机票之前隐藏一些有关机票的描述性特征，比如机票的来源、出发时间、经停地点等，直到乘客做出购买决定后才向其说明。

相关符号约定如下：

p _i 为航空公司 i( i=A、B)的定价； K， J分别为机票总供给和总需求， J＞ K供小于求，即高需求， J＜ K供大于求，即低需求； r为市场上品牌偏好的影响力； rx为乘客从航空公司A购买机票的距离成本， r(1– x)则表示从航空公司B购买机票的距离成本； $ \pi $ _I为中介的收益； $\pi _i^{\rm{T}}$ 为传统销售模式下航空公司 i的收益； $\pi _i^{\rm{O}}$ 为模糊销售机制下航空公司 i的收益； V/ r为乘客的购买意愿，反映2个航空公司的竞争程度。为确保乘客的效益非负，假设 V/ r≥1/2，类似于Jerath等^[6]。

$\varphi $ 为乘客对机票价值评价的折扣因子， $\varphi $ ∈[0, 1]， $\varphi $ =0表示乘客在未来购买机票的效用折扣为0，因此将完全忽视未来购买，即乘客是短视的。 $\varphi $ =1表示乘客在未来购买和现在购买的效用相同，即乘客是完全策略的。李豪^[9]、Levin等^[10]均采用此类假设。

还有以下进一步假设。

1)乘客和航空公司都是理性经济人，追求效用和收益最大化；

2)需求不确定，以 α的概率出现高需求即 J= H＞ K，以1– α的概率出现低需求即 J= L＜ K，且参数 α、 H、 L、 K是乘客和航空公司共识的；

3)理性预期均衡，即预期值和实际值相符。类似的假设有Muth^[11]和Dasu等^[12]。

2 传统销售

为了便于比较，本节首先分析在传统销售模式下考虑乘客策略行为的航空公司收益管理模型。处于Hotelling线上任意一点 x( x∈[0, 1])的乘客从航空公司A购买机票获得的效用为 V– rx– p _A，从航空公司B购买机票获得的效用为 V– r(1– x)– p _B。为得到航空公司收益和乘客的效用表达式，用 $p_i^1$ 表示航空公司 i在周期1的定价， $\pi _i^1$ 表示航空公司 i在周期1获得收益， $p_i^{2 \rm{L}}$ 表示航空公司 i在周期2低需求时的定价， $\pi _i^{2 \rm{L}}$ 表示航空公司 i在周期2低需求时获得的收益。

定理1

1)当 J＞ K时，航空公司在周期1的最优定价为 $p_{\rm{A}}^1 = p_{\rm{B}}^1 = V - \displaystyle\frac{{Kr}}{{2H}}$ ，最优市场覆盖率为 ${x_{\rm{A}}} = {x_{\rm{B}}} = \displaystyle\frac{K}{{2H}}$ ，航空公司的收益为 $\pi _{\rm{A}}^1 = \left( {V - \displaystyle\frac{{Kr}}{{2H}}} \right)\times \displaystyle\frac{K}{{2H}}\times H$ ，此时由于供小于求，航空公司在周期1将机票全部销售，因此没有剩余机票到周期2销售。

2)当 J< K时，Hotelling线上位于在[ x _A, x _B](其中 ${x_{\rm{A}}} = \displaystyle\frac{K}{{2H}}$ ， ${x_{\rm{B}}} = 1 - \displaystyle\frac{K}{{2H}}$ )的乘客在周期2购买机票，那么周期2航空公司的最优定价和最优市场覆盖率如 表1所示。

证明

1) J＞ K时，即需求大于供给时，为了避免在周期2买不到机票的风险，那么乘客会选择在周期1购买，此时航空公司的最优定价为 $p_{\rm{A}}^1 = p_{\rm{B}}^1 = V - \displaystyle\frac{{Kr}}{{2H}}$ ，航空公司A在周期1销售的机票数量为 $\displaystyle\frac{K}{{2H}} \times H$ ，其中 $H =\displaystyle \frac{K}{2}$ ，则航空公司A在周期1将所有机票售完，因此在周期2没有剩余机票。航空公司B的情况类似于A。

2) 航空公司A在周期1销售的机票数量为 $ {\displaystyle\frac{K}{{2H}}} \times L$ ，其中 $L {\text{＜}} \displaystyle\frac{K}{2}$ ，此时就会存在剩余机票在周期2销售。定义Hotelling线上某一点 $x_{\rm{A}}^{\rm{e}}$ 为周期1和周期2的边界乘客， $y_{\rm{A}}^{{\rm{L}},{\rm{e}}}$ 为低需求时周期2购买机票与不购买机票的边界乘客， $y_{\rm{A}}^{{\rm{L}},{\rm{e}}} {\text{≥}} x_{\rm{A}}^{\rm{e}}$ 。当 J＜ K时，航空公司A在周期2的定价为 $p_{\rm{A}}^{2{\rm{L}}} = \varphi V - y_{\rm{A}}^{\rm{L}}r$ ，且 $y_{\rm{A}}^{\rm{L}} {\text{＜}} \displaystyle\frac{1}{2}$ ，销售机票数量 $\left( {y_{\rm{A}}^{\rm{L}} - \displaystyle\frac{K}{{2H}}} \right)L$ ，获得利润为 $\pi _{\rm{A}}^{2{\rm{L}}} = \left( {\varphi V - y_{\rm{A}}^{\rm{L}}r} \right)$ × $\left( {y_{\rm{A}}^{\rm{L}} - \displaystyle\frac{K}{{2H}}} \right)L$ 。要使得利润最大，则 $y_{\rm{A}}^{\rm{L}} = \displaystyle\frac{{\varphi V + Kr/\left( {2H} \right)}}{{2r}}$ ， $p_{\rm{A}}^{2{\rm{L}}} = \displaystyle\frac{{\varphi V - Kr/\left( {2H} \right)}}{2}$ ， $\pi _{\rm{A}}^{2L} = \displaystyle\frac{{{{\left[ {\varphi V - Kr/\left( {2H} \right)} \right]}^2}}}{{4r}}L$ ，航空公司在周期1的定价为 $p_{\rm{A}}^1 = \alpha \left( {V - \displaystyle\frac{{Kr}}{{2H}} \cdot r} \right) + \left( {1 - \alpha } \right)$ × $ \displaystyle\frac{{\varphi V - Kr/\left( {2H} \right)}}{2}$ ， $\pi _{\rm{A}}^1 = p_{\rm{A}}^1\left[ {\alpha H + \left( {1 - \alpha } \right)L} \right]\displaystyle \frac{K}{{2H}}$ ，航空公司A的总收益就为 $\pi _{\rm{A}}^{\rm{T}} = \pi _{\rm{A}}^1 + \pi _{\rm{A}}^{2{\rm{L}}}$ ，整理得

$\begin{split}\\& \pi _{\rm{A}}^{\rm{T}} = \pi _{\rm{A}}^1 + \pi _{\rm{A}}^{2{\rm{L}}} = \left[ {\alpha \left( {V - \frac{{Kr}}{{2H}} \cdot r} \right) + \left( {1 - \alpha } \right)\frac{{\varphi V - Kr/\left( {2H} \right)}}{2}} \right] \times\\& \left[ {\alpha H + \left( {1 - \alpha } \right)L} \right]\frac{K}{{2H}} + \frac{{{{\left[ {\varphi V - Kr/\left( {2H} \right)}\right]}^2}}}{{4r}}L{\text{。}}\end{split}$

(1)

为使得 $y_{\rm{A}}^{2{\rm{L}}} {\text{≤}} 1/2$ ，给出限制条件 $ \displaystyle\frac{V}{r}{\text{＜}} 1 - \displaystyle\frac{K}{{2H}}$ 。

当 $1 - \displaystyle\frac{K}{{2H}} {\text{≤}} \displaystyle\frac{V}{r}{\text{＜}} \frac{3}{2}$ 时， $y_{\rm{A}}^{2{\rm{L}}} = 1/2$ ， $p_{\rm{A}}^{2{\rm{L}}} = \varphi V - r/2$ ， $p_{\rm{A}}^1 = \alpha \left( {V - \displaystyle\frac{{Kr}}{{2H}}} \right) + \left( {1 - \alpha } \right)\left( {V - \displaystyle\frac{r}{2}} \right)$ ， $\pi _{\rm{A}}^{2{\rm{L}}} = \left( {1 - \alpha } \right)\left( {\varphi V - \displaystyle\frac{r}{2}} \right)$ × $\left( {1 - \displaystyle\frac{K}{H}} \right) \displaystyle\frac{L}{2}$ ， $\pi _{\rm{A}}^1 = p_{\rm{A}}^1\left[ {\left( {\alpha H + \left( {1 - \alpha } \right)L} \right)} \right] \displaystyle\frac{K}{{2H}}$ ，那么航空公司的总收益为

$\begin{split}\\[-4pt]\pi _{\rm{A}}^{\rm{T}} = \pi _{\rm{A}}^1 + \pi _{\rm{A}}^{2{\rm{L}}} = \left[ {\alpha \left( {V - \frac{{Kr}}{{2H}}} \right) + \left( {1 - \alpha } \right)\left( {V - \frac{r}{2}} \right)} \right] \times \\\left[ {\left( {\alpha H + \left( {1 - \alpha } \right)L} \right)} \right]\frac{K}{{2H}} + \left( {1 - \alpha } \right)\left( {\varphi V - \frac{r}{2}} \right)\left( {1 - \frac{K}{H}} \right)\frac{L}{2}\text{。}\end{split}$

(2)

此时两航空公司的市场覆盖率恰好为1/2时，存在非竞争均衡。

当 $ \displaystyle\frac{3}{2}{\text{≤}} \displaystyle\frac{V}{r}$ 时， $y_{\rm{A}}^{2{\rm{L}}} = 1/2$ ， $p_{\rm{A}}^{2{\rm{L}}} = r$ ， $p_{\rm{A}}^1 = $ $\alpha \left( {V - \displaystyle\frac{{Kr}}{{2H}}} \right) + \left( {1 - \alpha } \right)r\,\text{，}$ $\pi _{\rm{A}}^{2{\rm{L}}} = \left( {1 - \alpha } \right)r\left( {1 - \displaystyle\frac{K}{H}} \right) \displaystyle\frac{L}{2}\,\text{，}$ $\pi _{\rm{A}}^1 = p_{\rm{A}}^1\left[ {\left( {\alpha H + \left( {1 - \alpha } \right)L} \right)} \right] \displaystyle\frac{K}{{2H}}$ ，那么航空公司的总收益为

$\begin{split}& \quad\quad \pi _{\rm{A}}^{\rm{T}} = \pi _{\rm{A}}^1 + \pi _{\rm{A}}^{2{\rm{L}}} = \left[ {\left( {V - \frac{{Kr}}{{2H}}} \right) + \left( {1 - \alpha } \right)r} \right]\times\\& \left[ {\left( {\alpha H + \left( {1 - \alpha } \right)L} \right)} \right]\frac{K}{{2H}} + \left( {1 - \alpha } \right)r\left( {1 - \frac{K}{H}} \right)\frac{L}{2}\text{。}\end{split}$

(3)

此时航空公司市场覆盖率为1/2，存在竞争均衡。

证毕。

在周期1，位于Hotelling线上 $[0,\frac{K}{{2H}}]$ 乘客对航空公司A偏好较大，则以较高的价格从航空公司A购买。当存在剩余机票时，在 $[\frac{K}{{2H}},\frac{1}{2}]$ 之间的乘客，即对航空公司A偏好较小，当航空公司A在周期2降低价格时，这部分乘客才购买。如果没有剩余机票，那么在周期2就没有任何销售。显然，理性的航空公司为实现收益最大化，在周期1会对偏好较大的乘客定价较高，然后在周期2降低价格，以吸引偏好较小的乘客。

3 模糊销售

本节主要分析航空公司实行模糊销售机制后的定价决策和期望收益。航空公司宣布在周期2实行模糊销售机制时，将剩余机票转移给中介I，由中介“出清”剩余机票。此时乘客会根据周期1的价格信息，预期周期2通过模糊销售能够购买到机票的概率以及机票来自哪个航空公司概率，然后决定当前购买还是延迟购买。只有在周期1结束至周期2开始时，乘客和航空公司才知道市场需求是高需求还是低需求。用 $p_{\rm{I}}^{\rm{H}}$ 表示高需求时中介的定价， $p_{\rm{I}}^{\rm{L}}$ 出现低需求时中介的定价。中介销售收入的 δ倍归提供其机票的航空公司所有，剩余1- δ部分归中介所有，且0≤ δ≤1。

当需求较低时，航空公司A剩余的机票期望数量为 $l_{\rm{A}}^{{\rm{L}},{\rm{e}}} = \max \left\{ {K/2 - x_{\rm{A}}^{\rm{e}}L,0} \right\}$ ，航空公司B剩余的机票期望数量为 $l_{\rm{B}}^{{\rm{L}},{\rm{e}}} = \max \left\{ {K/2 - \left( {1 - x_{\rm{B}}^{\rm{e}}} \right)L,0} \right\}$ ，那么乘客从模糊销售购买的机票来自航空公司A的概率为 $\gamma _{\rm{A}}^{{\rm{L}},{\rm{e}}} = l_{\rm{A}}^{{\rm{L}},{\rm{e}}}/\left( {l_{\rm{A}}^{{\rm{L}},{\rm{e}}} + l_{\rm{B}}^{{\rm{L}},{\rm{e}}}} \right)$ ，来自航空公司B的概率为 $\gamma _{\rm{B}}^{{\rm{L}},{\rm{e}}} = l_{\rm{B}}^{{\rm{L}},{\rm{e}}}/\left( {l_{\rm{A}}^{{\rm{L}},{\rm{e}}} + l_{\rm{B}}^{{\rm{L}},{\rm{e}}}} \right)$ 。同理，当需求较高时，航空公司A剩余的机票期望数量为 $l_{\rm{A}}^{{\rm{H}},{\rm{e}}} = \max \left\{ {K/2 - x_{\rm{A}}^{\rm{e}}H,0} \right\}$ ，航空公司B剩余的机票期望数量为 $l_{\rm{B}}^{{\rm{H}},{\rm{e}}} = $ max $\left\{ {K/2 - \left( {1 - x_{\rm{B}}^{\rm{e}}} \right)H,0} \right\}$ ，那么乘客从模糊销售购买的机票来自航空公司A的概率为 $\gamma _{\rm{A}}^{{\rm{H}},{\rm{e}}} = l_{\rm{A}}^{{\rm{H}},{\rm{e}}}/\left( {l_{\rm{A}}^{{\rm{H}},{\rm{e}}} + l_{\rm{B}}^{{\rm{H}},{\rm{e}}}} \right)$ ，来自航空公司B的概率为 $\gamma _{\rm{B}}^{{\rm{H}},{\rm{e}}} = l_{\rm{B}}^{{\rm{H}},{\rm{e}}}/\left( {l_{\rm{A}}^{{\rm{H}},{\rm{e}}} + l_{\rm{B}}^{{\rm{H}},{\rm{e}}}} \right)$ 。

乘客基于中介的价格 p _I、获得机票的概率 $\gamma _{\rm{A}}^{\rm{e}}$ 、 $\gamma _{\rm{B}}^{\rm{e}}$ 以及在Hotelling线上所处的位置这几方面因素来决定是否从中介购买机票。

引理1 在理性预期均衡下，当2个公司所持有的机票数量相同时，且有可能出现高需求时：

$\quad\quad \gamma _{\rm{A}}^{\rm{H}} = \gamma _{\rm{B}}^{\rm{H}} = \gamma _{\rm{A}}^{\rm{L}} = \gamma _{\rm{B}}^{\rm{L}} = 1/2{\text{。}}$

证明

为了便于分析，采用逆推归纳法。假定[ x _A, x _B]之间的乘客等待至周期2购买，在周期2开始时，市场需求已被乘客和中介所知晓。当供大于求时，中介定价为 $p_{\rm{I}}^{\rm{L}}$ ；供小于求时，中介定价为 $p_{\rm{I}}^{\rm{H}}$ 。在理性预期均衡下，可以得到 ${\gamma _{\rm{A}}} = {\gamma _{\rm{B}}} = 1/2$ ，证明类似于Jerath等^[6]，这里不再赘述。因此，位于[ x _A, x _B]之间的乘客，从中介购买的机票来自任意航空公司的均衡期望为 $\gamma _{\rm{A}}^{\rm{H}} = \gamma _{\rm{B}}^{\rm{H}} = \gamma _{\rm{A}}^{\rm{L}} = \gamma _{\rm{B}}^{\rm{L}} = 1/2$ 。

接着分析对于 $[0,{x_{\rm{A}}}) \cup ({x_{\rm{B}}},1]$ 之间的乘客也有同样的均衡期望。假定位于 x _A左边的任意乘客 x，其从航空公司A购买机票获得效用为 V- p _A- rx，当其从中介购买机票的期望效用为 $\alpha \Bigl[\varphi V - p_{\rm{I}}^{\rm{H}} - \gamma _{\rm{A}}^{{\rm{H}},{\rm{e}}}rx - \gamma _{\rm{B}}^{{\rm{H}},{\rm{e}}} $ $r(1 - x)\Bigl] + (1 - \alpha )\Bigl [\varphi V - p_{\rm{I}}^{\rm{L}} - \gamma _{\rm{A}}^{{\rm{L}},{\rm{e}}}rx - \gamma _{\rm{B}}^{{\rm{L}},{\rm{e}}}r(1 - x)\Bigl]$ ，只要模糊销售市场上存在潜在的乘客，那么模糊销售市场上的机票由2个航空公司各提供一半，因此，处于点 x＜ x _A的乘客的期望效用为 $\alpha (\varphi V - p_{\rm{I}}^{\rm{H}} - r/2) + $ $(1 - \alpha )(\varphi V - p_{\rm{I}}^{\rm{L}} - r/2)$ ，位于点 x＞ x _B的乘客类似于 x＜ x _A。

证毕。

根据引理1，可得如下定理：

定理2 当 $ \displaystyle\frac{1}{2} {\text{≤}} \displaystyle\frac{V}{r} {\text{≤}} \displaystyle\frac{K}{H}$ 时，航空公司的最优定价为 ${p_{\rm{A}}} = {p_{\rm{B}}} = \displaystyle\frac{V}{2}$ ，最优市场覆盖率为 ${x_{\rm{A}}} = 1 - {x_{\rm{B}}} = \displaystyle\frac{V}{{2r}}$ ，中介的最优定价为 $p_{\rm{I}}^{\rm{L}} = p_{\rm{I}}^{\rm{H}} = \varphi V - \displaystyle\frac{r}{2}$ ，中介的期望收益为

$\begin{split}\\[-5pt]& \quad\quad\pi _{\rm{I}}^{} = \left( {1 - \delta } \right)\biggr[\alpha \left( {\varphi V - \frac{r}{2}} \right)\left( {K - \frac{{VH}}{{2r}}} \right)r + \\& \left( {1 - \alpha } \right)\left( {\varphi V - \frac{r}{2}} \right)\left( {1 - \frac{V}{{2r}}} \right)Lr \biggr]\text{。}\end{split}$

(4)

航空公司的期望总收益为

$\begin{split}\\[-3pt]& \quad\quad \pi _{\rm{A}}^{\rm{O}} = \pi _{\rm{B}}^{\rm{O}} = \displaystyle\frac{{{V^2}}}{{4r}} \bigg[ {\alpha H + \left( {1 - \alpha } \right)L} \bigg] + \\& \displaystyle\frac{1}{2}\delta \biggr[\alpha (\varphi V \!-\! \frac{r}{2})(K \!-\! \displaystyle\frac{{VH}}{{2r}})r + \left( {1 \!-\! \alpha } \right)(\varphi V \!-\! \displaystyle\frac{r}{2})(1 - \frac{V}{{2r}})Lr \biggr]{\text{。}}\end{split}$

(5)

证明

在需求确定情况下，策略乘客不会使航空公司通过模糊销售来提高周期1的价格，因此航空公司要满足周期1的需求，则 ${x_{\rm{A}}} {\text{≤}} \frac{K}{{2H}}$ ， ${x_{\rm{B}}} {\text{≥}} 1 - \frac{K}{{2H}}$ ，那么航空公司A的定价就为 ${p_{\rm{A}}} = V - {x_{\rm{A}}}r$ ，航空公司B定价为 ${p_{\rm{B}}} = V - \left( {1 - {x_{\rm{B}}}} \right)r$ ，则两个航空公司市场覆盖率的最优均衡为 ${x_{\rm{A}}} = 1 - {x_{\rm{B}}} = \displaystyle\frac{V}{{2r}}$ ，价格均衡为 ${p_{\rm{A}}} = {p_{\rm{B}}} = \displaystyle\frac{V}{2}$ 。

当出现高需求时，通过模糊销售的机票数量为 $K - \displaystyle\frac{{VH}}{{2r}}$ ，低需求时通过模糊销售的机票数量为 $L - \displaystyle\frac{{VL}}{{2r}}$ ，由引理1 $\gamma _{\rm{A}}^{{\rm{H}},{\rm{e}}} = \gamma _{\rm{A}}^{{\rm{L}},{\rm{e}}} = \displaystyle\frac{1}{2}$ ，那么中介的价格就为 $p_{\rm{I}}^{\rm{H}} = p_{\rm{I}}^{\rm{L}} = \varphi V - \displaystyle\frac{r}{2}$ ，整理可得中介的期望收益如式(4)，航空公司的收益为如式(5)。

证毕。

定理3 当 $ \displaystyle\frac{K}{H} {\text{≤}} \frac{V}{r} {\text{≤}} \displaystyle\frac{K}{H} + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{{2L}}$ 时，不论是高需求还是低需求，航空公司的最优定价为 ${p_{\rm{A}}} = {p_{\rm{B}}} = V - \displaystyle\frac{{Kr}}{{2H}}$ ，市场最优覆盖率为 ${x_{\rm{A}}} = 1 - {x_{\rm{B}}} = \displaystyle\frac{K}{{2H}}$ 。当 J＜ K时，中介的最优定价为 $p_{\rm{I}}^{\rm{L}} = \varphi V - \displaystyle\frac{r}{2}$ ，那么中介的期望收益为

$\quad\quad {\pi _{\rm{I}}} = \left( {1 - \delta } \right)\left( {\varphi V - \frac{r}{2}} \right)\left( {1 - \frac{K}{H}} \right)Lr\text{。}$

(6)

航空公司的期望总收益为

$\begin{split}\\[-4pt]& \quad\quad \pi _{\rm{A}}^{\rm{O}} = \pi _{\rm{B}}^{\rm{O}} = \left( {V - \frac{{Kr}}{{2H}}} \right)\left[ {\alpha \frac{K}{{2H}}H + \left( {1 - \alpha } \right)\frac{K}{{2H}}L} \right] + \\& \frac{1}{2}\delta \left( {1 - \alpha } \right)\left( {\varphi V - \frac{r}{2}} \right)\left( {1 - \frac{K}{H}} \right)Lr{\text{。}}\end{split}$

(7)

证明

在这种情况下，2个航空公司通过竞争得到市场均衡覆盖率 ${x_{\rm{A}}} = 1 - {x_{\rm{B}}} = \displaystyle\frac{K}{{2H}}$ ，均衡价为 ${p_{\rm{A}}} = {p_{\rm{B}}} = $ $V - \displaystyle\frac{{Kr}}{{2H}}$ 。当 J＞ K时，没有剩余机票进行模糊销售。当 J＜ K时，剩余机票数量为 $\left( {{x_{\rm{A}}} - {x_{\rm{B}}}} \right)L = (1 - \displaystyle\frac{K}{{2H}} - \frac{K}{{2H}})L$ ，中介的最优定价为 $p_{\rm{I}}^{\rm{L}} = \varphi V - \displaystyle\frac{r}{2}$ ，整理得中介的期望收益为如式(6)，那么航空公司的收益如式(7)所示。

证毕。

定理4

当 $ \displaystyle\frac{K}{H} + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \frac{K}{{2L}} {\text{≤}} \displaystyle\frac{V}{r} {\text{＜}}1 + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{{2L}}$ 时，航空公司最优定价为 ${p_{\rm{A}}} = {p_{\rm{B}}} = \displaystyle\frac{V}{2} + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \frac{K}{{4L}}r$ ，当 J＞ K时，市场最优覆盖率为 $\displaystyle\frac{K}{{2H}}$ ，当 J＜ K时，市场最优覆盖率为 $\displaystyle\frac{V}{{2r}} - \frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{{4L}}$ ，中介的最优定价为 $p_{\rm{I}}^{\rm{L}} = \varphi V - \displaystyle\frac{r}{2}$ ，因此中介的期望收益为

$\quad\quad {\pi _{\rm{I}}} = \left( {1 - \delta } \right)\left( {\varphi V - \frac{r}{2}} \right)\left( {1 - \frac{V}{r} + \frac{\alpha }{{1 - \alpha }}\times \frac{K}{{2L}}} \right)Lr \text{。}$

(8)

航空公司的期望收益为

$\begin{array}{l}\quad\quad \pi _{\rm{A}}^{\rm{O}} = \pi _{\rm{B}}^{\rm{O}} = (\displaystyle\frac{V}{2} + \displaystyle\frac{\alpha }{{1 - \alpha }} \cdot \frac{K}{{4L}}r)\biggr[\alpha \displaystyle\frac{K}{{2H}}H + \left( {1 - \alpha } \right) \times\\[8pt](\displaystyle\frac{V}{{2r}} - \displaystyle\frac{\alpha }{{1 - \alpha }} \cdot \frac{K}{{4L}})\biggr] + \displaystyle\frac{1}{2}\delta \left( {1 - \alpha } \right)\left( {\varphi V - \displaystyle\frac{r}{2}} \right)\times\end{array}$

$\quad\quad \left( {1 - \frac{V}{r} + \frac{\alpha }{{1 - \alpha }} \times \frac{K}{{2L}}} \right)Lr{\text{。}}$

(9)

证明

由于 $ \displaystyle\frac{V}{r} {\text{≤}} 1 + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{{2L}}$ ，此时2个航空公司的均衡价为 ${p_{\rm{A}}} = {p_{\rm{B}}} = \displaystyle\frac{V}{2} + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{{4L}}r$ ，当 J＞ K时，市场最优覆盖率为 $ \displaystyle\frac{K}{{2H}}$ ，此时无剩余机票进行模糊销售。当 J＜ K时，市场最优覆盖率为 $ \displaystyle\frac{V}{{2r}} - \displaystyle\frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{{4L}}$ ，可得剩余机票的数量为 $1 - \displaystyle\frac{V}{r} + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \frac{K}{{2L}}$ ，整理可得定理4。

证毕。

定理5

当 $1 + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{{2L}} {\text{≤}} \displaystyle\frac{V}{r} {\text{＜}} \displaystyle\frac{3}{2} + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \frac{K}{L}$ 时，航空公司最优定价为 ${p_{\rm{A}}} = {p_{\rm{B}}} = V - \displaystyle\frac{r}{2}$ ，当 J＞ K时，市场最优覆盖率为 $ \displaystyle\frac{K}{{2H}}$ ，当 J< K时，市场最优覆盖率为 $ \displaystyle\frac{1}{2}$ ，航空公司的期望总收益为 $\pi _{\rm{A}}^{\rm{O}} = \pi _{\rm{B}}^{\rm{O}} = \left( {\displaystyle\frac{V}{r} - \displaystyle\frac{1}{2}} \right)$ × $\left[ {\alpha \displaystyle\frac{K}{2} + \left( {1 - \alpha } \right) \displaystyle\frac{L}{2}} \right]r$ 。

证明

在这种情形下，乘客购买意愿较大，整个市场被两个航空公司占领，那么其均衡价为 ${p_{\rm{A}}} = {p_{\rm{B}}} = $ $V - \displaystyle\frac{1}{2}$ ，当 J＞ K时，航空公司的最优市场覆盖率为 $ \displaystyle\frac{K}{{2H}}$ ，当 J＜ K时，航空公司各占领一半的市场，则不存在剩余机票，因此没有模糊销售的必要。

证毕。

定理6 当 $ \displaystyle\frac{3}{2} + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{L} {\text{≤}} \displaystyle\frac{V}{r}$ 时，航空公司最优定价为 ${p_{\rm{A}}} = {p_{\rm{B}}} = \left( {1 + \displaystyle\frac{\alpha }{{1 - \alpha }}\times \displaystyle\frac{K}{L}} \right)r$ ，获得期望总收益为 $\pi _{\rm{A}}^{\rm{O}} = \pi _{\rm{B}}^{\rm{O}} = \left( {1 + \displaystyle\frac{\alpha }{{1 - \alpha }} \cdot \displaystyle\frac{K}{L}} \right)\left[ {\alpha \displaystyle\frac{K}{2} + \left( {1 - \alpha } \right) \displaystyle\frac{L}{2}} \right]r$ 。

证明

当 J> K时，航空公司的最优市场覆盖率为 $\displaystyle\frac{K}{{2H}}$ ，当 J< K时，航空公司通过竞争确定市场覆盖率得到 ${x_{\rm{A}}} = \displaystyle\frac{1}{2} + \displaystyle\frac{{{p_{\rm{A}}} - {p_{\rm{B}}}}}{{2r}}$ 。显然不论是高需求还是低需求，都没有剩余机票进行模糊销售。那么航空公司A、B的收益为 $\pi _{\rm{A}}^{\rm{O}} = {p_{\rm{A}}}\left[ {\alpha \displaystyle\frac{K}{2} + \left( {1 - \alpha } \right)\left( {\frac{1}{2} + \frac{{{p_{\rm{B}}} - {p_{\rm{A}}}}}{{2r}}} \right)} \right]$ ， $\pi _{\rm{B}}^{\rm{O}} = {p_{\rm{B}}}\left[ {\alpha \displaystyle\frac{K}{2} + \left( {1 - \alpha } \right)\left( {\frac{1}{2} + \frac{{{p_{\rm{A}}} - {p_{\rm{B}}}}}{{2r}}} \right)} \right]$ ，整理可得 ${p_{\rm{A}}} = {p_{\rm{B}}} = \left( {1 + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{L}} \right)r$ ， ${x_{\rm{A}}} = {x_{\rm{B}}} = \displaystyle\frac{1}{2}$ 。

则有 $\pi _{\rm{A}}^{\rm{O}} = \pi _{\rm{B}}^{\rm{O}} = \left( {1 + \displaystyle\frac{\alpha }{{1 - \alpha }} \times \displaystyle\frac{K}{L}} \right)\left[ {\alpha \displaystyle\frac{K}{2} + \left( {1 - \alpha } \right) \displaystyle\frac{L}{2}} \right]r$ ，要使得均衡价存在，那么位于Hotelling线上1/2处的乘客的效用非负，那么 $V \!-\! {p_{\rm{A}}} \!-\! \displaystyle\frac{r}{2} {\text{≥}} 0 \Rightarrow \displaystyle\frac{V}{r} {\text{≥}} \displaystyle\frac{3}{2} \!+\! \displaystyle\frac{\alpha }{{1 \!-\! \alpha }} \times \frac{K}{L}$ ，这与本文之前的假设相符。

证毕。

在需求不确定情况下，乘客由于不知道周期1的需求情况，考虑到如果周期2需求较高，则票价较高，因此有可能不会选择等待。也就是说，如果乘客从周期1购买机票获得的效用，比其在周期2因高需求购买机票所得的效用要高，甚至于出现买不到机票的情况时，乘客则会选择在周期1购买。航空公司鉴于乘客这样的考虑，因此在周期1定较高的价格，以获得更大的收益。此时如果实际需求较低，虽然航空公司在周期1只能销售部分机票，但可以通过模糊销售，“出清”剩余机票。

当 α越大时，即出现高需求的概率越高时，航空公司更愿意使用模糊销售。原因很简单， α越大，乘客为购买到机票而竞争，会抬高周期1的票价，显然此时航空公司在周期1应该定较高的价格。当实际需求确实较高时，航空公司则获得较大的收益。若实际需求较小，则会存在一部分因周期1高价格而未购买机票的乘客，此时，航空公司则通过模糊销售将机票售出。

4 算例分析

本节通过数值模拟(利用Maple18)验证以上理论分析的结果，重点分析模糊销售机制对航空公司收益的影响以及对乘客策略程度缓解效果。

基本参数设置如下：假设航空公司和中介之间平分模糊销售阶段的收益即 δ=1/2。不失一般性，假定 r=2， K=1， α=1/2， L=1/2， H=3/2。

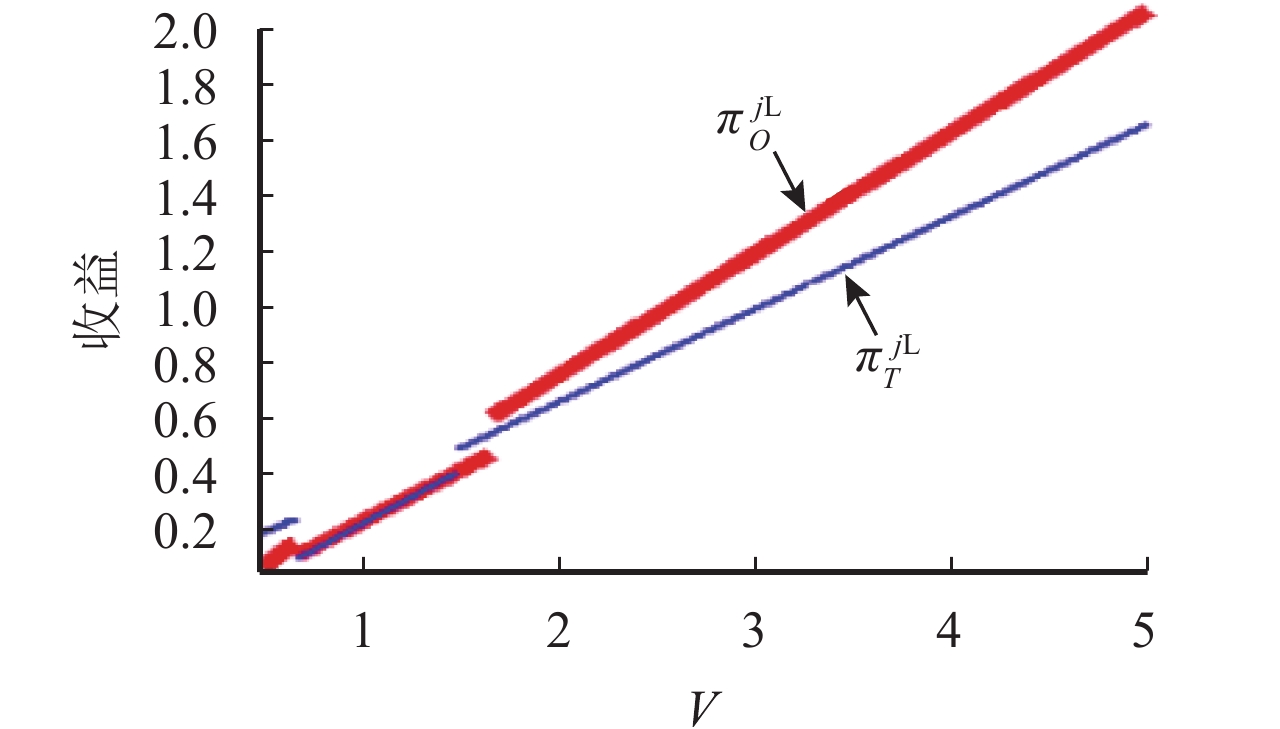
4.1 2种销售机制下乘客估价 V对航空公司收益的影响

首先假定乘客是完全策略的，即 φ=1，模拟乘客估价 V与航空公司收益的关系，如 图2所示。

从 图2可看到，乘客的估价与航空公司的收益呈正相关。当乘客估价非常低时，航空公司采用传统销售模式获得的收益更高，随着乘客估价的上升，模糊销售机制下的收益逐步高于传统销售机制。从整体来看，当乘客具有完全策略行为时，模糊销售机制获得收益高于传统销售。

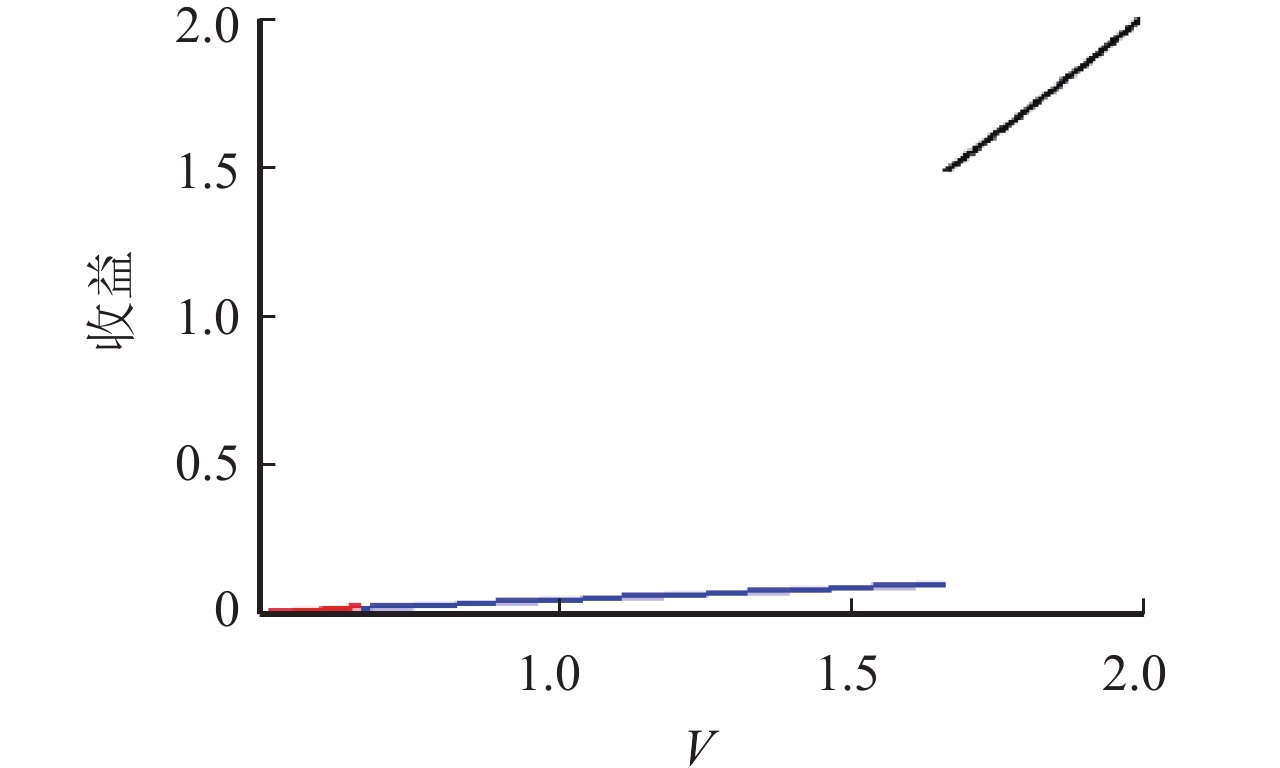
4.2 模糊销售机制下乘客估价 V与中介收益的关系

保持其他参数不变，模拟乘客估价 V与中介收益的关系，如 图3所示。

从 图3可以看到，在模糊销售机制下，中介的收益随着乘客估价的增加而增加，且中介的收益恒大于0，意味着中介有实施模糊销售的动力，尤其是当乘客估价较高时，中介实施模糊销售机制能获取较高的收益。因此，模糊销售机制具有可行性。

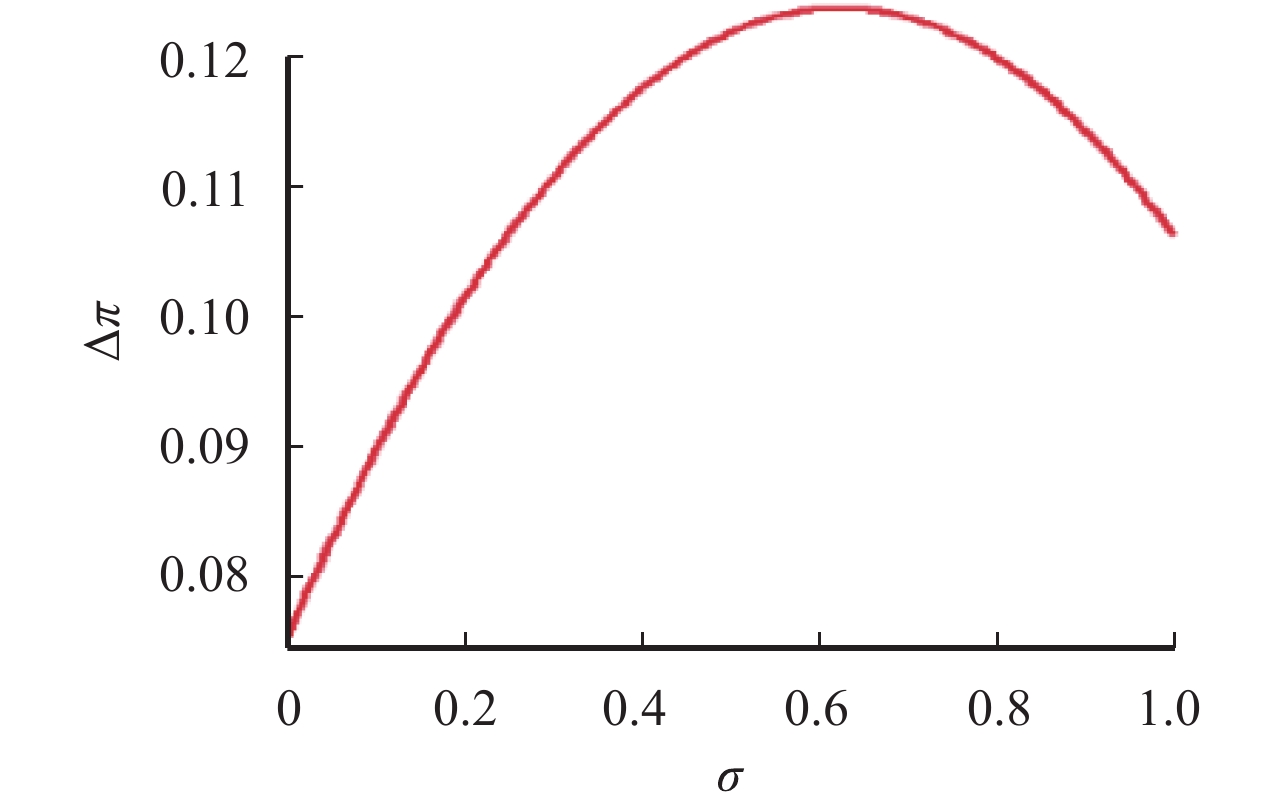
4.3 乘客策略程度 φ对模糊销售机制有效性的影响

令 $\Delta \pi = \pi _{\rm{A}}^0 - \pi _{\rm{A}}^{\rm{T}}$ ，不失一般性，取 V=1，保持其他参数不变，模拟乘客策略程度 φ与航空公司收益的关系，如 图4所示。

从 图4看到，当 $\varphi \in \left( {0,1} \right]$ 时，2种策略的收益差 $\Delta \pi $ 恒为正，也就是说模糊销售机制具有有效性。同时还可以看到，随着策略程度的增加，收益差在某一点取得最大值，然后开始下降。这是因为，当乘客策略程度超过某一临界值时，航空公司将更多的机票给予中介销售，那么中介分得的收益较多，相对而言减少了航空公司的总体收益。

5 结论

本文研究在需求不确定下考虑乘客策略行为的航空收益管理问题。在乘客具有策略行为的假设下，在航空机票销售中引入模糊销售机制。将整个机票销售分为2个周期，周期1为传统销售，周期2航空公司实行模糊销售机制，即周期1结束后，航空公司将所剩机票转给中介，由中介“出清”剩余机票。

根据问题的特点，本文利用Hotelling模型建立了需求不确定下考虑乘客策略行为的航空公司收益管理模型。研究了航空公司在传统销售和模糊销售机制下的市场最优价格、市场占有率以及期望收益。通过比较航空公司在2种销售机制下的收益，得出了模糊销售机制能够缓解乘客的策略行为，可以提高航空公司收益。并通过数值模拟从航空公司和中介的视角分析了模糊销售机制的有效性。

本文只是尝试将模糊销售引入航空公司应对策略乘客的机制中，还有如下问题可继续深入研究：首先，本文只考虑了2个相互竞争的航空公司。而某一航线上可能有有限个航空公司进行竞争，多个航空公司竞争的研究将更具实践意义；其次，当乘客的估价服从某一分布时，航空公司又该如何决策。