交通运输部发布的统计公报显示，截至2015年底，我国高速公路总里程达1.17×10⁵ km，已经超过美国，居世界第一。我国高速公路的建设已取得巨大成就，但养护管理工作却严重滞后。现阶段对高速公路的日常养护往往依赖人工决策，缺乏科学的规划手段和精确有效的决策方法，对人力、物力的资源利用率都很低，导致较高的养护成本，不利于我国公路事业高速发展的需要。本文研究高速公路日常养护管理中最基本的决策问题，即养护车辆路径优化问题，研究其在不确定性环境下的建模方法和优化算法，为决策者提供科学的决策方法。本文将该问题定义为一个带随机服务时间和随机移动时间的带容量约束的弧路径规划问题。

带容量约束的弧路径规划问题 (capacitated arc routing problem，CARP) 最早由Golden和Wong^[1]提出，之后该问题在学术上引起广泛关注。关于CARP的研究文献已有很多，而自Fleury等^[2-3]首次提出带随机变量的CARP以来，至今对该问题的研究仍非常有限。在现实环境中，由于受到多种因素，如顾客需求、天气情况、交通拥挤和车辆故障等影响，信息往往是不确定的。目前关于不确定性CARP的研究绝大多数只关注需求的不确定性。Chris-tiansen等^[4]描述了需求服从泊松分布的随机CARP，优化目标是获得期望费用最小的路径，通过分支定价法求得精确解。Laporte等^[5]以垃圾收集问题为例研究了带随机需求的CARP，在考虑修正费用的情况下提出自适应大规模邻域搜索算法构建解决方案。Wang等^[6]考虑了弧上的需求及费用的随机性，提出了一种文化基因算法及其改进算法，能够获得问题的鲁棒解。González等^[7]提出一种模拟与启发式算法相结合的方法，将蒙特卡洛模拟与求解确定限量弧路径问题的基于随机存储的启发式方法RandSHARP结合起来，用于求解带随机需求的弧路径问题。

关于带随机需求变量的CARP的研究已较为全面，但在现实生活中，影响路径决策的还有车辆移动时间及服务时间的不确定性、服务费用的不确定性和提供服务的车辆、司机的不确定性等，而鲜有对带这些随机变量的CARP的研究。Tagmouti等^[8]也只是将需求弧上的服务费用定义为与时间相关的分段线性函数，先将弧路径问题转化成点路径问题，再使用列生成方法求解相应的CARP。

目前尚无关于带随机时间变量的CARP的研究，但有不少关于带随机时间变量的车辆路径规划问题 (vehicle routing problem，VRP) 的研究。Li等^[9]也利用机会约束模型和带修正的随机规划模型描述带随机时间变量的VRP，利用改进的禁忌搜索算法对问题进行求解。Zhang等^[10]假设每条弧上的移动时间服从正态分布，将问题抽象为机会约束模型，利用分散搜索算法和基因算法求解。Taş等^[11]构造了一个带随机移动时间和软服务时间窗的模型，使用禁忌搜索和事后优化的多层次方法求解模型。Miranda等^[12]考虑带硬时间窗及随机时间的VRP，并提出一种基于迭代局域搜索的元启发式方法，在保证一定服务质量的同时使成本最小。Errico等^[13]将带硬时间窗及随机服务时间的VRP描述为集合划分问题，考虑两种不同的修正策略，提出最新的分支切割定价方法进行求解。从理论上来讲，大多数CARP问题都可以转化成CVRP再进行求解，但往往会使求解过程更复杂，算法的性能也无法得到保证。

关于弧路径问题的求解方法，很多文献中都使用了邻域搜索算法，这是求解组合优化问题中一种简单且鲁棒性较强的方法。Beullens等^[14]提出一种新的搜索算法，元启发式引导的邻域搜索算法，并进一步使用邻域列表和边标记的机理，提高了解的质量。Polacek等^[15]使用变邻域搜索算法研究带中转站的CARP，仅在邻域搜索中增加交叉交换这一种交换操作，就获得了鲁棒性不错的解。Tang等^[16]将基因算法和拓展的邻域搜索相结合，更有效地搜索了解空间，避免解陷入局部最优。

1 问题建模

本节针对高速公路日常养护问题，首先建立一个机会约束规划模型 (chance-constrained programming model, CCPM) 对问题进行定义。模型定义养护车辆的总工作时长超过某个给定阈值的概率，优化目标是总服务费用最小化。在此基础上，进一步提出一个带修正的随机规划模型 (stochastic program-ming model with recourse, SPM-R)，即允许养护车辆超时工作和延期工作，通过合理设计修正措施使得总的服务费用最小化。

1.1 机会约束规划模型CCPM

一个高速路网可以定义为一个有向图G=(V,A,R)，其中，V=( ${v_0}$ , ${v_1}$ ,…, ${v_n}$ )代表顶点集合 ( ${v_0}$ 为养护站)， $A = ({a_{ij}},i,j \in V)$ 代表顶点间的有向弧集， $R \subset A$ 为需求弧 (即需要养护的弧) 的集合，R中每条弧都必须被服务一次。另外，定义K=(k₁,k₂,…,k_m )为车辆集。由于各种因素，如事故、交通状况和天气情况的影响，各条弧上的移动时间存在不确定性。同样，需求弧上的养护服务时间也会受到道路状况、事故和养护人员的技术水平等因素影响，存在不确定性。假设：1) 每条路径的起始点和终点都是养护站；2) 当养护车辆行驶过一条弧而没对它进行养护服务时，称为空车行驶；3) 最短路径定义为养护站与第一条服务弧之间的路径、任意两条连续服务弧之间的路径以及最后一条服务弧与养护站之间的路径。

模型中的参数定义如下。

O(v)：离开点v的弧集， $v \in V$ ；

I(v)：进入点v的弧集， $v \in V$ ；

S：弧的子集；

V(S)：经过子集S中弧的车辆集；

d_a ：弧a的长度， $a \in A$ ；

t_a ：弧a上的移动时间， $a \in A$ ，假设t_a 是一个服从正态分布的连续随机变量 ${t_a}\~N\left( {{\mu _{t,a}}{\rm{}}\sigma _{t,a}^2} \right)$ ；

s_a ：弧a上的服务时间， $a \in R$ ，假设s_a 是一个服从正态分布的连续随机变量 ${s_a}\~N({\mu _{s,a}},\sigma _{s,a}^2)$ ；

B：每辆车每回合最大允许工作时间；

α：随机约束能容忍的概率，也表示置信水平；

λ：单位移动成本；

f：使用车辆的单位固定成本。

决策变量如下。

x_ak ：=1，如果需求弧a由车k服务；否则=0， $a \in R$ ， $k \in K$ ；

y_ak ：车k穿越弧a的次数， $a \in A$ ， $k \in K$ ；

z_k ：=1，如果使用了车k；否则=0， $k \in K$ 。

CCPM可以描述如下。

$\min D = \min ({D_1} + {D_2}) = \min (f\sum\limits_{k \in K} {{z_k}} + \lambda \sum\limits_{k \in K} {\sum\limits_{a \in A} {{d_a}{y_{ak}}} } )。$

(1)

约束条件为

$\quad\quad \sum\limits_{k \in K} {{x_{ak}}} = 1,\forall a \in R{\text{，}}$

(2)

$\quad\quad \mathop \sum \limits_{a \in O\left( v \right)} \left( {{x_{ak}} \!+\! {y_{ak}}} \right) \!-\! \mathop \sum \limits_{a \in I\left( v \right)} \left( {{x_{ak}} + {y_{ak}}} \right) \!=\! 0,\forall v \in V,k \in K{\text{，}}$

(3)

$\quad\quad \mathop \sum \limits_{a \in O\left( 0 \right)} \left( {{x_{ak}} + {y_{ak}}} \right) {\text{≥}} {z_k},\forall k \in K{\text{,}}$

(4)

$\begin{split}& \quad\quad \sum\limits_{a \in O\left( {V\left( S \right)} \right)} {\left( {{x_{ak}} + {y_{ak}}} \right)} {\text{≥}} {x_{bk}},\forall S \subset A,0 \notin V\left( S \right),\\& 2 {\text{≤}} \left| S \right| {\text{≤}} \left| V \right| - 1,b \in S \cap R,k \in K{\text{，}}\end{split}$

(5)

$\quad\quad {z_k} {\text{≥}} \frac{1}{{\left| R \right|}}\mathop \sum \limits_{a \in R} {x_{ak}},\forall k \in K{\text{，}}$

(6)

$\quad\quad P\left\{ {\mathop \sum \limits_{a \in R} {s_a}{x_{ak}} + \mathop \sum \limits_{a \in A} {t_a}{y_{ak}} {\text{≤}} B} \right\} {\text{≥}} \alpha ,\forall k \in K{\text{，}}$

(7)

$\quad\quad {x_{ak}},{z_k} \in \left\{ {0,1} \right\},\forall a \in R,k \in K{\text{，}}$

(8)

$\quad\quad {y_{ak}} {\text{≥}} 0,{\text{整数}},\forall a \in A,k \in K{\text{。}}$

(9)

当移动时间t_a 和服务时间s_a 相互独立且均服从正态分布，约束 (7) 中的机会约束可以表示为

$\begin{split}& \quad\quad {\varphi ^{ - 1}}\left( \alpha \right)\sqrt {\sum\limits_{i = 0}^{{n_k}} {\left[ {V\left( {{t_{{a_i}}}} \right) + V\left( {{s_{{a_i}}}} \right)} \right]} } + \\& \sum\limits_{i = 0}^{{n_k}} {\left[ {E\left( {{t_{{a_i}}}} \right) + E\left( {{s_{{a_i}}}} \right)} \right]} {\text{≤}} B,\forall k \in K{\text{。}}\end{split}$

(10)

其中，φ是标准正态分布函数；E(•)和V(•)代表随机变量的期望和方差。

目标函数 (1) 最小化车辆的固定费用和空驶费用之和。约束 (2) 确保需求弧集中的每条弧都被服务一次。约束 (3) 和 (4) 确保每辆被使用的车必须从养护站出发并最终回到养护站。约束 (5) 是连通性约束，即如果车k服务子集S中的某条弧，那么它必定穿过S的边界。约束 (6) 表示每辆被使用的车至少需要服务一条弧。约束 (7) 给出一个机会约束条件，确保每辆车的总工作时间小于规定的最大工作时间B的概率为α。约束 (8) 和 (9) 定义了变量的特性。

1.2 带修正的随机规划模型SPM-R

SPM-R模型允许养护车辆不满足机会约束 (10)，但通过定义修正措施使得总成本 (包括服务费用和修正费用) 最小化。定义 ${\tau ^k}$ 为养护车辆k的路径， ${\tau ^k}$ 由一系列弧a_n^k (服务弧和空驶弧) 构成， ${\tau ^k}{\rm{ = }}\{ 0,a_1^k,a_2^k,...,a_n^k,0\} $ 。

SPM-R是一个两阶段随机规划模型。第一阶段对养护车辆路径集合τ进行决策；第二阶段在获得服务时间和移动时间的真实数据后，定义修正措施对养护车辆的路径进行修正。SPM-R的优化目标是最小化总费用，包括第一阶段的总服务费用和第二阶段的期望修正费用 $E\left[ {\varphi \left( \tau \right)} \right]$ 。

当车辆在路径上的总工作时间超过了规定的最大工作时间B时，该路径被称为失效的路径计划。为计算期望修正费用，首先需要计算车辆服务路径计划的失效概率。路径计划失效既可能发生在某条服务弧上，也可能发生在非服务弧上。

参数定义如下。

$a_x^k$ ：车k的路径上的第x条弧， $k \in K$ ， $x = 1,2, \ldots ,{n_k}$ ；

$T\left( {k,a_x^k} \right)$ ：车k到达弧 $a_x^k$ 终点的总工作时间；

$L\left( {a_x^k,0} \right)$ ：车k从弧 $a_x^k$ 到养护站的移动时间

ρ：延期服务的单位距离修正成本；

θ：超时工作的单位距离修正成本。

$T\left( {k,a_x^k} \right)$ 包括需求弧的总服务时间和总行驶时间。因为t_a 和s_a 是相互独立的服从正态分布的随机变量，因此 $T\left( {k,a_x^k} \right)$ 也服从正态分布，期望和方差分别为

$\quad\quad E\left[ {T\left( {k,a_x^k} \right)} \right] = \sum\limits_{i = 0}^x {\left( {{\mu _{t,a_i^k}} + {\mu _{s,a_i^k}}} \right)}{\text{，}}$

(11)

$\quad\quad V\left[ {T\left( {k,a_x^k} \right)} \right] = \sum\limits_{i = 0}^x {\left( {\sigma _{t,a_i^k}^2 + \sigma _{s,a_i^k}^2} \right)}{\text{。}}$

(12)

定义 $P\left( {k,a_x^k} \right) = P\left\{ {\left[ {T\left( {k,a_x^k} \right) + L\left( {a_x^k,0} \right)} \right] {\text{＜}}B} \right\}$ ，当 $P\left( {k,a_x^k} \right) {\text{＜}} \alpha $ 时，意味养护路径计划在弧a_x^k 发生失败。此时，假设a_y^k 为a_x^k 前的最后一条服务弧，修正措施定义如下。

修正措施 (R) ：车辆k从弧a_y^k 的终点返回养护站，返回途中对途经的服务弧进行养护服务。定义 $\overline {{\tau ^k}} $ 为原计划安排在 $a_y^k$ 之后的弧集合， $\overline{\overline {{\tau ^k}}} $ 为在车k返回养护站途中服务的弧集合， $\overline{\overline {{\tau ^k}}} \subset \overline {{\tau ^k}} $ 。 $\overline {{\tau ^k}} $ 中未被服务的弧将被安排在第二天进行服务。

路径 ${\tau ^k}$ 的期望修正费用可以定义如下，包括超时惩罚费用和延期惩罚费用：

$\quad\quad E\left[ {\varphi \left( {{\tau ^k}} \right)} \right] = \theta \sum\limits_{{a_i} \in \overline{\overline {{\tau ^k}}} } {{d_{{a_i}}}} + \rho \sum\limits_{{a_i} \in \overline {{\tau ^k}} - \overline{\overline {{\tau ^k}}} } {{d_{{a_j}}}}{\text{。}}$

(13)

因此，SPM-R模型表达如下：在给定一个路径计划 $\tau = \left( {{\tau ^1}, \ldots ,{\tau ^{\left| K \right|}}} \right)$ 的情况下，最小化解τ中车辆固定费用 ${D_1}\left( \tau \right)$ 、空驶费用 ${D_2}\left( \tau \right)$ 和期望修正费用 $E\left[ {\varphi \left( \tau \right)} \right]$ 的总和。

$\begin{split}& \quad\quad \min \left[ {D\left( \tau \right) + E[\varphi (\tau )]} \right] = \\& \min \left\{ {f\sum\limits_{k \in K} {{z_k}} + \lambda \sum\limits_{k \in K} {\sum\limits_{a \in A} {{d_a}{y_{ak}}} } + \sum\limits_{k \in K} E [\varphi (\tau )]} \right\}{\text{。}}\end{split}$

(14)

约束条件：式(2)～(6)、式(8)～(13)。

2 分支切割法

本节使用分支切割 (branch-and-cut，B&C) 法对CCPM进行求解，首先对连通性约束和机会约束进行松弛，如果所求得的解为非可行解，则加入新的约束排除这个非可行解，重复该过程直到获得的解也是原模型的可行解。

针对连通性约束 (5)，参照Hà等^[17]提出的切割方法，利用启发式的分割程序来识别非整数解时的连通性违反。具体步骤如下。当求得一个非整数解，所有决策变量 $\left\{ {{x_{ak}},{y_{ak}}} \right\}$ 需要重新调整。通过连接那些满足 ${x_{ak}} + {y_{ak}} {\text{≥}} \omega $ 的弧来构造网络，其中，ω是一个预定义的值，且 $0 {\text{≤}} \omega {\text{＜}} 1$ ，将得到的图定义为 $G'$ 。如果 $G'$ 不是弱连通，那么与 $G'$ 中的每个弱连通分量相关的连通性不等式被确定为连通性违反。在文献[17]中，Hà等证明了这种启发式的切割方法比其他切割方法和未使用切割的分支定界法能更快获得更好的下界。

而约束 (10) 定义的机会约束是非线性的，无法直接用于识别非可行解。利用一个二元变量替代原有的整数变量 ${y_{ak}}$ ：

$\quad\quad {y_{ak}} = \sum_{i = 1}^{u(a)} {{2^{i - 1}}{\theta _{iak}}} ,\forall a \in A,k \in K{\text{，}}$

(15)

$\quad\quad {\theta _{iak}} \in \left\{ {0,1} \right\},\forall a \in A,k \in K,i = 1, \ldots ,u\left( a \right){\text{。}}$

(16)

令M_a 为y_ak 的上界，u(a)表示为

$\quad\quad u\left( a \right) = \left\{ \begin{array}{l}\begin{array}{*{20}{c}}{1,{M_a} = 0{\text{；}}}\\[5pt]{\left[ {\log _2^{{M_a}}} \right] + 1,{M_a} \ne 0{\text{；}}}\end{array}\\[5pt]\forall a \in A{\text{。}}\end{array} \right.$

(17)

M_a 可以估算为

$\quad\quad {M_a} = \left\{ {\begin{array}{*{20}{c}}{\left| R \right| + 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a \in A\backslash R{\text{；}}}\\{\left| R \right|,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a \in R{\text{。}}}\end{array}} \right.$

(18)

如果车辆k'的路径是一条非可行路径，可以通过以下约束将其排除：

$\quad\quad \sum\limits_{i:\theta {'_{iak'}} = 1} {\left( {1 - {\theta _{iak}}} \right) {\text{≥}} 1} {\text{。}}$

(19)

另外，将以下约束引入模型：

$\quad\quad {z_k} {\text{≥}} {z_{k + 1}},1 {\text{≤}} k {\text{≤}} \left| K \right| - 1{\text{,}}$

(20)

$\quad\quad \sum\limits_{i = 1}^j {{2^{j - i}}{x_{ik}}} \! {\text{≥}}\! \sum\limits_{i = 1}^j {{2^{j - i}}{x_{i,k + 1}}} ,\forall j \in R,1 \!{\text{≤}}\! k \!{\text{≤}}\! \left| K \right| - 1{\text{。}}$

(21)

分支切割算法的关键在于忽略原问题 (CCPM) 中的非线性约束 (5) 和 (10)，先求解新问题 (CCPM’)。

$\min D \!=\! \min \left( {{D_1} + {D_2}} \right) \!=\! \min \left( {f\sum\limits_{k \in K} {{z_k}} \!+\! \lambda \sum\limits_{k \in K} {\sum\limits_{a \in A} {{d_a}{y_{ak}}} } } \right){\text{。}}$

(22)

约束条件：式(2)～(4)、式(6)、式(8)、式(15)、式(16)、式(20) 和式(21) 以及

$\quad\quad {y_{ak}} {\text{≥}} 0,\forall a \in A,k \in K{\text{。}}$

(23)

求解CCPM’后，通过增加约束 (19) 更新CCPM’的约束集，再次求解CCPM’，持续迭代直到得到的CCPM’的最优解也满足CCPM。

分支切割法对解决小规模问题非常高效，但很难获得大规模问题的精确解。因此，本文提出一种启发式算法求解中大规模问题，并根据分支切割法获得的最优解验证该启发式算法的性能。

3 自适应大规模邻域搜索算法

自适应大规模邻域搜索 (adaptive large neighborhood search，ALNS) 算法是大规模邻域搜索的扩展，它提供多个具有竞争关系的删除算法和插入算法。每一个删除及插入算法都有一个权重，控制搜索过程中被调用的概率。这些权重在搜索过程中不断调整，使算法更具适应性。ALNS算法的要点描述如下。

3.1 初始解

首先利用改进的路径扫描 (path scanning, PS) 法求初始解。PS法描述如下。

1) 设定k=1，R'=R；

2) 在路径 ${\tau ^k}$ 中插入顶点0，即 ${\tau ^k}$ ={0}；

3) 令 $c \in R'$ 为最接近当前路径 ${\tau ^k}$ 终点的弧；

4) 如果将弧c插入路径 ${\tau ^k}$ 后满足工作时间约束，那么将c添加在路径 ${\tau ^k}$ 末尾，并将c从集合R'中删除并执行(5)；否则关闭当前路径 (关闭路径是指将所有属于路径终点到养护站间最短路径中的弧插入路径中)，k=k+1，返回(2)；

5) 如果 $R' = \emptyset $ ，关闭路径 ${\tau ^k}$ 并终止算法，否则返回(3)。当算法终止时，k即为方案所需总车辆数。

3.2 自适应搜索

ALNS算法的一次迭代包括：从当前路径中选择一种删除算法删除q条服务弧，然后选择一种插入算法将其重新插入路径。每次迭代时，基于轮盘赌原则选择删除算法和插入算法。此外，每经过γ次迭代，删除算法和插入算法的权重就更新一次，所有算法的初始权重都为0。

对每次迭代后获得的解计算目标函数值，即式(14) 的值。假设F^*是当前的最优目标函数值，令τ'为解τ的一个邻域，定义F(τ')为解τ'的目标函数值。若 $F\left( {\tau '} \right) {\text{＜}} {F^*} + \delta {F^*}$ ，则接受解τ'为下一次迭代初始解，其中δ为容忍偏差，是一个给定的正参数。若 $F\left( {\tau '} \right) {\text{＜}} {F^{\rm{*}}}$ ，那么更新当前最优解F^*。当经过一定的迭代次数仍不能优化F^*，或者总的迭代次数达到设定值时，算法终止。

3.3 删除算法

1) 确定性最差删除算法 (deterministic worst removal, DWR) ：假设 $D\left( {{\tau ^k}} \right)$ 为 ${\tau ^k}$ 的确定费用 (固定费用和空车行驶费用之和)，定义 $D\left( {{\tau ^k}, - a_i^k} \right)$ 为删除弧 $a_i^k$ 后路径的确定费用， $\Delta D$ 为删除后节省的费用。

$\quad\quad \Delta D = D\left( {{\tau ^k}} \right) - D\left( {{\tau ^k}, - a_i^k} \right),\forall i = 1,2, \ldots ,{n_k},\forall k \in K{\text{。}}$

DWR启发算法选择产生最大 $\Delta D$ 的服务弧a_i^k ，直到删除q条服务弧。

2) 确定性随机删除算法 (deterministic random removal, DRR) ：随机删除服务弧a_i^k ，直到删除完q条服务弧。

3) 减少车辆数量的删除算法 (reduce-number-of-vehicle removal, RNR) ：定义n_s,k 为路径 ${\tau ^k}$ 中服务弧的数量， $k = 1,2, \ldots ,\left| K \right|$ 。RNR算法的计算步骤如下。

①将当前路径按n_s,k 的非减顺序排列；

②将路径τ¹中的所有服务弧都删除，同时删除该路径。

3.4 插入算法

1) 确定性贪婪插入算法 (deterministic greedy insertion, DGI) ：设删除弧集合为X，对插入的每条弧 $x\left( {x \in X} \right)$ ，定义 $D\left( {{\tau ^k}, + x} \right)$ 为将弧x插入路径 ${\tau ^k}$ 后的确定费用 (满足时间约束)。定义 $\Delta D$ 为由插入操作引起的费用增量，最好的插入位置是在插入x后引起费用增加最小的位置。

2) 概率贪婪插入算法 (probabilistic greedy insertion 1, PGI 1) ：对于每条要被插入的弧x来说，令 $P\left( {{\tau ^k}, + x} \right)$ 为将弧x插入到路径 ${\tau ^k}$ 最佳位置后的总作业时间小于给定阈值B的概率。最佳插入位置满足如下条件：①在插入x后增加的确定费用最小；② $P\left( {{\tau ^k}, + x} \right)$ 大于置信水平α。算法终止条件与DGI相同。

3) 概率贪婪插入算法 (probabilistic greedy insertion 2, PGI 2) ：PGI 2与PGI 1的唯一区别是插入位置的选择不同，它的最佳插入位置是使总费用最小。

4 数据实验

本节设计了一系列具有不同参数的随机算例进行数据实验，首先通过求解小规模问题的CCPM对ALNS算法的性能进行评价，然后通过使用ALNS方法对比CCPM和SPM-R 2个模型的优劣并分析算法对随机变量的敏感性。计算机配置为：Intel CORE CPU @2.53GHz, 4.0GHz, 2.0GB RAM，ALNS算法由Visual C#编程实现，B&C算法由CPLEX12.5 Callable Library实现。

4.1 小规模算例

随机构造一个网络图，生成参数不同的多个算例，设置过程如下。

1)在100×100的平面随机产生5~25个顶点，并随机选择一个点作为养护站。

2) 随机产生一条汉密尔顿回路，确保养护站与其余各点间的存在往返路径，然后再从每个点随机引出1~4条弧与其他点相连，构成一个强连通的网络。在所有弧中随机选择一定比例的需求弧。以欧氏距离定义弧的距离d_a (km)。

3) 每条弧上移动时间的平均值 ${\mu _{t,a}}$ (min)定义为0.8d_a ，标准差 ${\sigma _{t,a}}$ 定义为0.1 ${\mu _{t,a}}$ ，变异系数CV为0.1 (CV是指标准差与平均值的比值)。

4) 需求弧上服务时间的平均值 ${\mu _{s,a}}$ 定义为2 ${\mu _{t,a}}$ ，标准差 ${\sigma _{s,a}}$ 定义为0.1 ${\mu _{s,a}}$ ，CV为0.1。

5) 每辆车的最大允许工作时间B设置为480，置信水平α设置为90%。

6) 单位移动费用λ设置为5，超时工作的单位费用θ设置为10，延期服务的单位修正费用ρ设置为20，每辆车的固定费用f设置为200。

7)将最优解得不到改进的迭代次数和总迭代次数分别设置为3 000和5 000，将每次迭代去除的弧数量q设置为需求弧数量的1/3，并设置δ=10%。

为评估ALNS算法的求解性能，分别用ALNS算法与B&C算法求解机会约束规划模型，并对2个算法求得的最优解进行比较。表1是2种算法求解4组小规模问题 (G1-G4) 的结果，每一组随机生成10个算例。

表1中，“|V|”列表示路网的顶点数量；“|R|”列表示需求弧数量；“|A|”列表示所有弧数量，B&C中的“#OPT”列表示B&C算法在每组算例内获得最优解的次数；ALNS中的“#OPT”列表示ALNS算法求得与B&C算法解相同的算例数，即ALNS算法获得最优解的次数；“CPU(s)”列表示求解每组算例计算机的平均运算时间。B&C算法在求解某些算例时无法在1 h内获得最优解，这种情况下，使用B&C算法在1 h内计算得到的最优上界作为比较对象。“Gap(%)”列表示ALNS解与B&C最优上界之间的平均相对误差。

由以上结果可知，B&C算法总共可以获得40个算例中的30个最优解，而ALNS算法获得29个最优解。ALNS解与B&C最优上届之间的平均误差在1.45%~3.15%之间。由于B&C算法是一种精确解法，在小规模问题中能求解出的解必然比ALNS算法好，但实验证明了这个差距并不大，说明ALNS算法具有很好的准确度。而且相比B&C算法，ALNS算法在运算时间上有明显的优势，具有更高的效率。因此，相比B&C等精确算法，ALNS算法更适合被用于求解中大规模问题。

4.2 实际算例

为了比较在中大规模问题下CCPM和SPM-R的优劣，以及分析ALNS算法对置信水平α和变异系数CV这两个重要变量的敏感性，将ALNS算法应用于上海快速路网日常维护中的车辆路径规划问题，分别对CCPM和SPM-R模型进行求解。图1为上海市快速道路网的示意图，共31个点，104条有向弧。图中的箭头方向表示道路的方向性，点1设为养护站。在所有弧中随机选择50%的弧作为需求弧。各条弧的长度由实际距离获得，车辆的平均移动速度设为60km/h，服务速度设为30km/h，其他参数与4.1节相同。

4.2.1 CCPM与SPM-R比较

应用ALNS算法求解图1所示路网的养护服务路径规划问题，取CV=0.1，α=90%，每次随机选取不同的需求弧，分别构造10个算例。计算结果见表2。

其中，“D₁”、“D₂”、“ $E\left[ {\varphi \left( \pi \right)} \right]$ ”和“D”分别表示车辆固定费用、空驶费用、期望修正费用和总费用；“Imp(%)”表示SPM-R方案比CCPM方案总费用减少的百分比。由表2的结果可知：

1) 在CCPM模型中，为满足机会约束，需要较多的车辆，而在SPM-R中，需要相对较少的车辆，因此即使需要支付修正费用，仍能使总费用减少。SPM-R方案比CCPM方案的总费用平均节省6.59%。

2) 以上实验均假设允许将未完成的养护服务推迟至第2天进行。然而在某些情况下，当服务质量比成本更为重要时，即不允许推迟服务，则机会约束必须得到满足，此时无法使用SPM-R模型。

3) 从计算效率的观点来看，ALNS算法只需不到30 min就解决了表2中的所有算例，体现了ALNS算法的优越性。

4.2.2 敏感性分析

1) 置信水平α

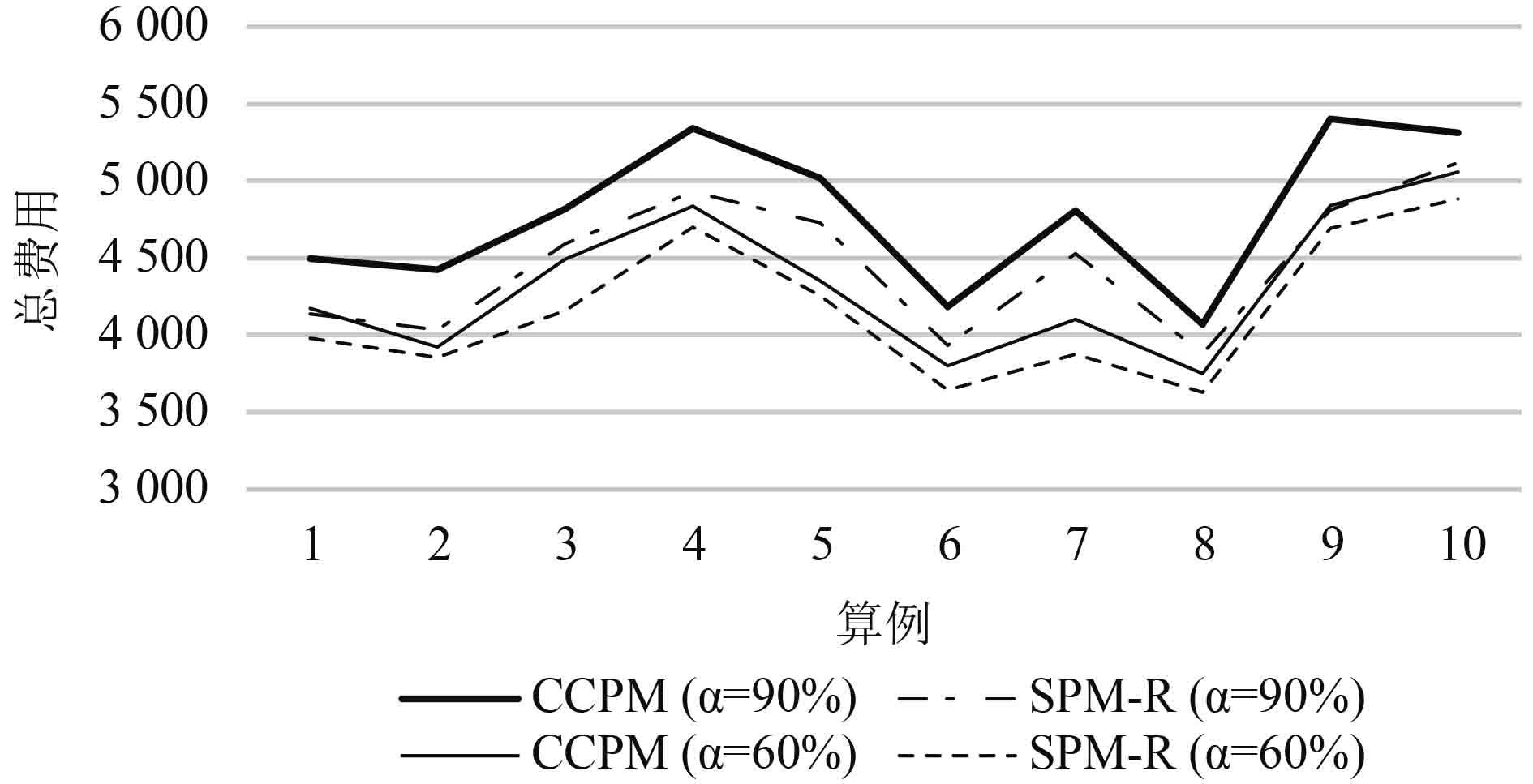
针对表2中的算例，保持CV=0.1，服务水平α取60%，对比结果如图2。

由图2的对比结果可知：

①对所有算例来说，CCPM和SPM-R模型在α=60%时的结果均优于在α=90%时的结果。

②α=90%时，SPM-R模型相比CCPM模型的解平均优化6.59%，而α=60%时，只优化了3.78%。

这是由于随着置信水平α减小，机会约束的限制小了，可以使用较少的养护车辆，因此CCPM模型的成本下降了。也由于限制变小，违反机会约束的修正费用也会减少，导致SPM-R模型成本的下降，同时也使SPM-R模型的优化效果减弱了。

2) 变异系数CV

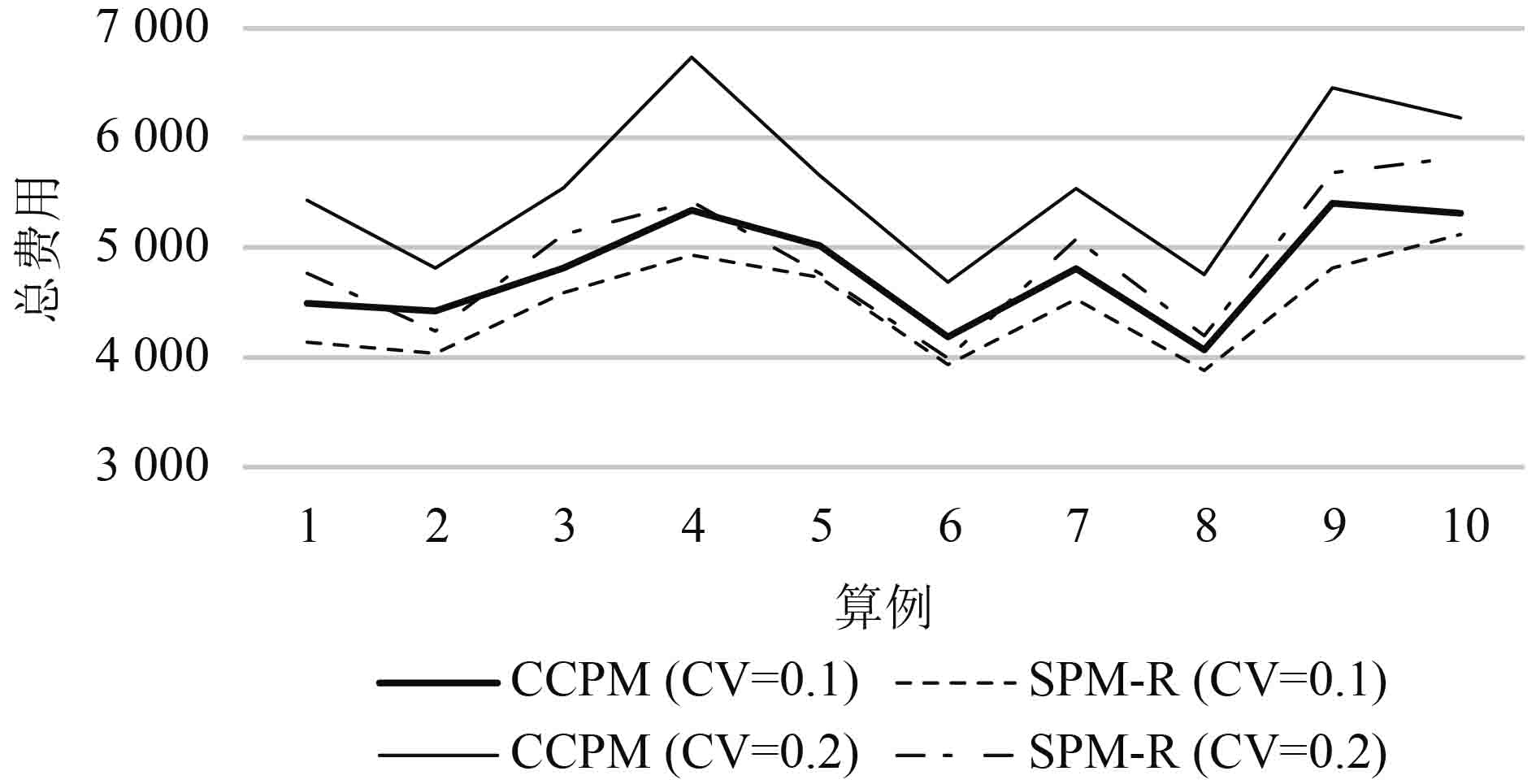
同样针对表2中的算例，保持服务水平α=90%，CV分别取0.1，0.2，对比结果如图3所示。

由图3的对比结果可知：

①CCPM和SPM-R模型在CV=0.2时的总成本均比在CV=0.1时有所提高。

②CV=0.2时，SPM-R模型相比CCPM模型的解平均优化11.86%，明显好于CV=0.1时的6.59%。

变异系数CV的增大，说明系统的不确定性增大，空车行驶距离会增大，机会约束也更容易违反，修正费用增加，总成本必然提高。同时也说明SPM-R模型比CCPM模型更能适应不确定性较大的系统。

6 结论

本文研究高速路网日常维护中的养护车辆路径优化问题，并考虑车辆在服务弧上的服务时间和非服务弧上的移动时间的不确定性。首先提出一个机会约束规划模型，使用分支切割算法进行求解。然后进一步提出一个带修正的随机规划模型，考虑养护计划失败情况下的修正费用，并提出自适应大规模邻域搜索算法求解中大规模问题。通过与B&C算法所得到的精确解比较，证明了ALNS算法的有效性和高效性。并将ALNS算法应用于真实的快速路网，通过算例证明了在特定情况下带修正的随机规划模型的优越性，还对2个重要随机变量的敏感性进行了分析。本文为高速公路的养护车辆路径优化问题提供了新的解决思路和途径，可将研究成果应用于高速公路日常维护管理和优化决策的实际工作。

今后的研究可以考虑在不确定性情况下获得鲁棒性解，因为对期望表现的关注往往忽视了与极端情况相关的风险。更进一步地，可以考虑动态的时间变量，时间变量实时变化而非符合特定的概率分布，更符合现实中的路径问题。