面向资源的定制型生产企业，生产模式为面向订单生产(made to order，MTO)，其生产环境具有许多随机不确定性，如订单到达、加工时间等，这导致各工序间在制品数量通常较多，生产现场物料搬运任务繁重。为了提高搬运效率，很多定制生产企业通常采用AMHU(如AGV小车，以下简称小车)作为在制品转序的运输工具。为了保证工作中心尽可能少地出现停工待料，小车并不需要等到装满再进行搬运，即小车的装载批量具有一定的随机性。当加工中心前的缓存区容量不足时，小车将因无法一次性卸载所有工件而处于等待状态；同时，加工中心后的缓存区如果达到最大缓存量，加工中心将因无法卸载工件而被堵塞。这些都给此类制造系统的建模带来了较大的困难。

对制造系统排队网建模问题，国内外学者进行了广泛的研究。其中文献[1]研究了小车每次运输一个工件的情况，利用普通的单服务台排队网进行近似求解；文献[2]证明了批处理的调度策略在一定条件下可近似当作保留一定关键性策略的标准单服务台排队网来处理。文献[3]分析了晶圆制造自动化物料运输系统特点，并提出了改进的开排队网模型，文献[4]综述了近年来基于排队网理论的批量到达与批量处理模型的建模及求解方法。以上批处理研究都是针对批量为常数的情况，而实际批处理问题的批量往往都是不确定的。在批量为变量的批处理问题研究上，文献[5]介绍了的M^X /G^Y /1/N的排队网模型的建立与求解方法，文献[6]与文献[7]将M^X /G^Y /1/N模型扩展到了一般分布与非马尔科夫过程中，但是模型都建立在单个节点上，忽略了节点之间的相互作业对系统产生的影响。文献[8]针对工件到达速率与批量分别依赖于队列长度与服务批次大小的排队网模型，通过嵌入马尔科夫链进行了近似求解。文献[9]针对具有储运单元的柔性流水车间进行了性能分析，采用改良状态空间分解法进行了近似求解，其小车往返于两点之间，且加工节点不考虑本身阻塞情况。

综述表明，目前在对制造系统的排队网建模研究方面，并没有此类小车按照环形路径进行随机批量运输，且考虑小车和加工单元阻塞情况的研究。对于排队网问题的研究，常用的方法主要有精确法^[10]、状态空间分解法^[11]与扩展法^[12-13]。针对本文描述的制造系统，由于小车的状态直接影响着生产过程的各个环节，因此分析小车与各环节状态之间的关系非常关键，本文拟采用状态空间分解法求解该问题。

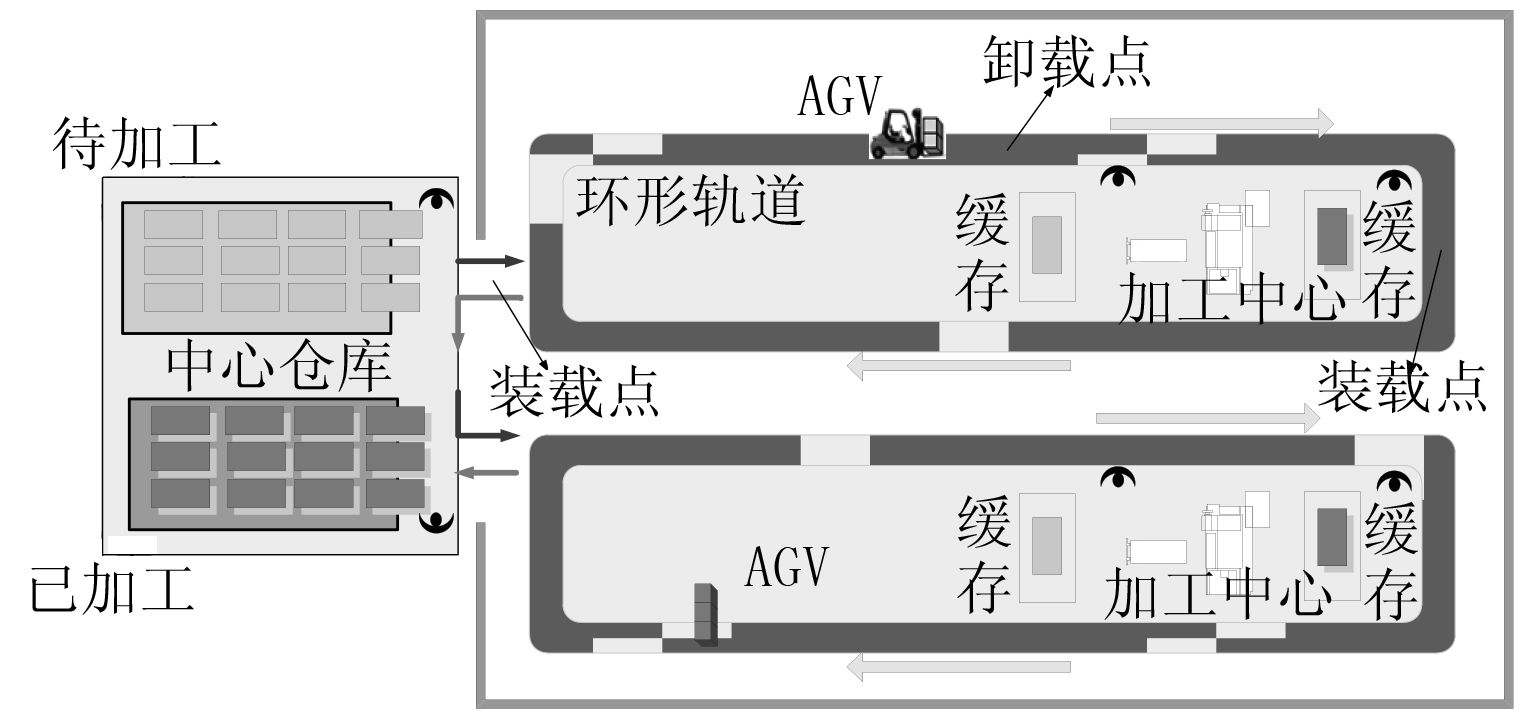
1 问题描述与简化模型

根据实际调研，抽象出如图1所示的定制生产企业生产车间，该生产车间主要由生产环节、运输环节和缓存设施三部分组成。小车从中心仓库将工件运输到产线前端卸载，等待加工；然后行驶至产线后端，将加工完的工件从缓存区搬离产线，运回到中心仓库。每辆小车服务于一条生产线，不混合装载。因此只需要考虑小车与其服务的生产线，即对单条生产线进行研究。

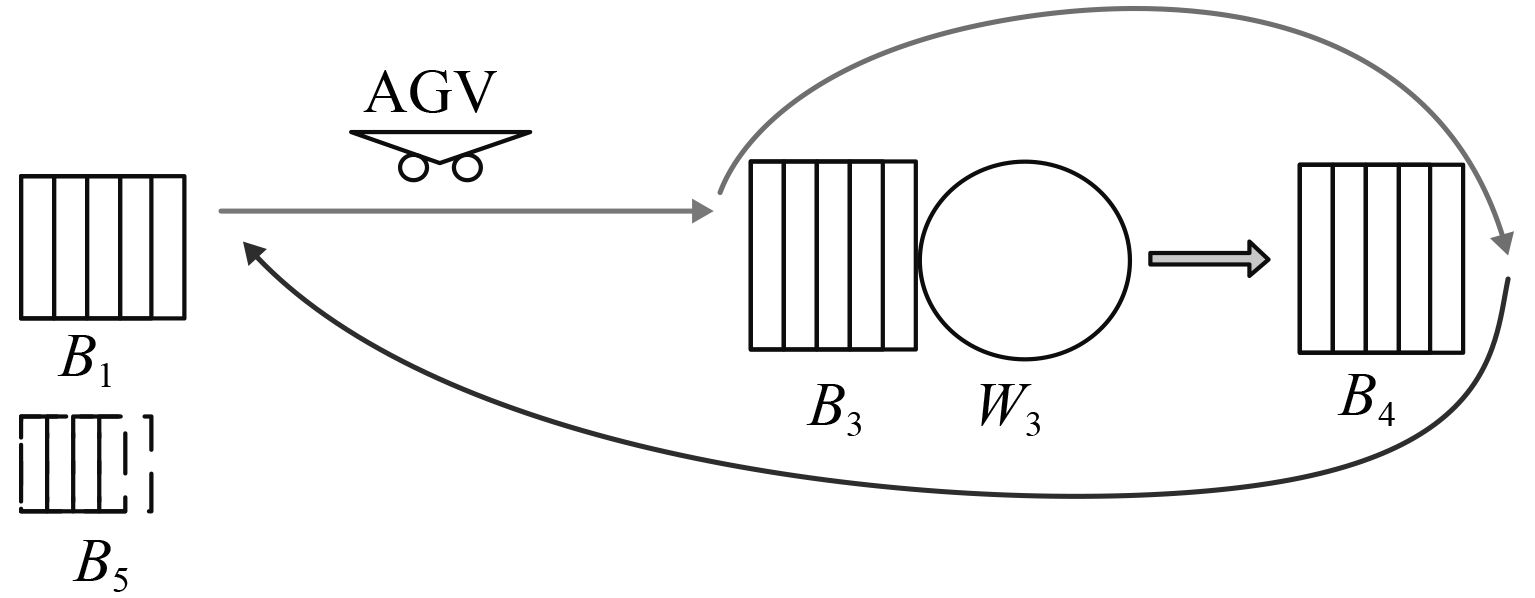
如图2是基于分段环形路径的制造系统所建立的排队网系统模型。假设系统由中心仓库B₁、搬运小车AGV、加工中心(B₃，W₃)和暂存区B₄组成。工件随机从B₁进入系统，经过加工后由小车从B₄运离至完工工件库B₅，离开系统。由于完工工件一般能够直接出厂或者投入其他工序环节，可假定B₅为容量为无限大的缓存。为了符合开排队网对节点的基本要求，在符合实际制造系统生产规则的前提下，特作以下假设。

1) 工件以服从参数为λ₁的泊松分布进入系统，每个工件之间都是相互独立的。

2) 当一个工件来到系统，它将直接进入B₁，小车到达之前，它将进入等待队列，如果B₁装满，工件将被拒绝；小车每次装载1至C个工件。

3) 节点3只有一台机器，只能同时加工1个工件，其加工时间相互独立且服从参数为μ₃的指数分布(包括装夹、准备时间)。

4) 小车将工件从B₁运送到B₃的时间与从B₃行驶至缓存B₄，以及从B₄将工件运离系统的时间均服从参数为V指数分布，且每次运行之间是相互独立的。

5) 每个缓存区(B₁、B₃、B₄)是有限容量的，设其最大容量为N_i ，i=1，3，4；

6) 小车到达B₁/B₄时，如果B₁/B₄没有工件，将等待至有一个工件到达B₁/B₄并直接装上后再前往B₃/B₅，否则直接将B₁/B₄中的工件搬离，装车时间忽略不计。

7) 小车到达B₃时，如果B₃空位不足，小车将等待空位，直到所有工件卸下；否则不在B₃处停留，将所有的工件直接卸下，卸载时间忽略不计。

8) 服务原则是先到先服务；阻塞服从后阻塞机制。

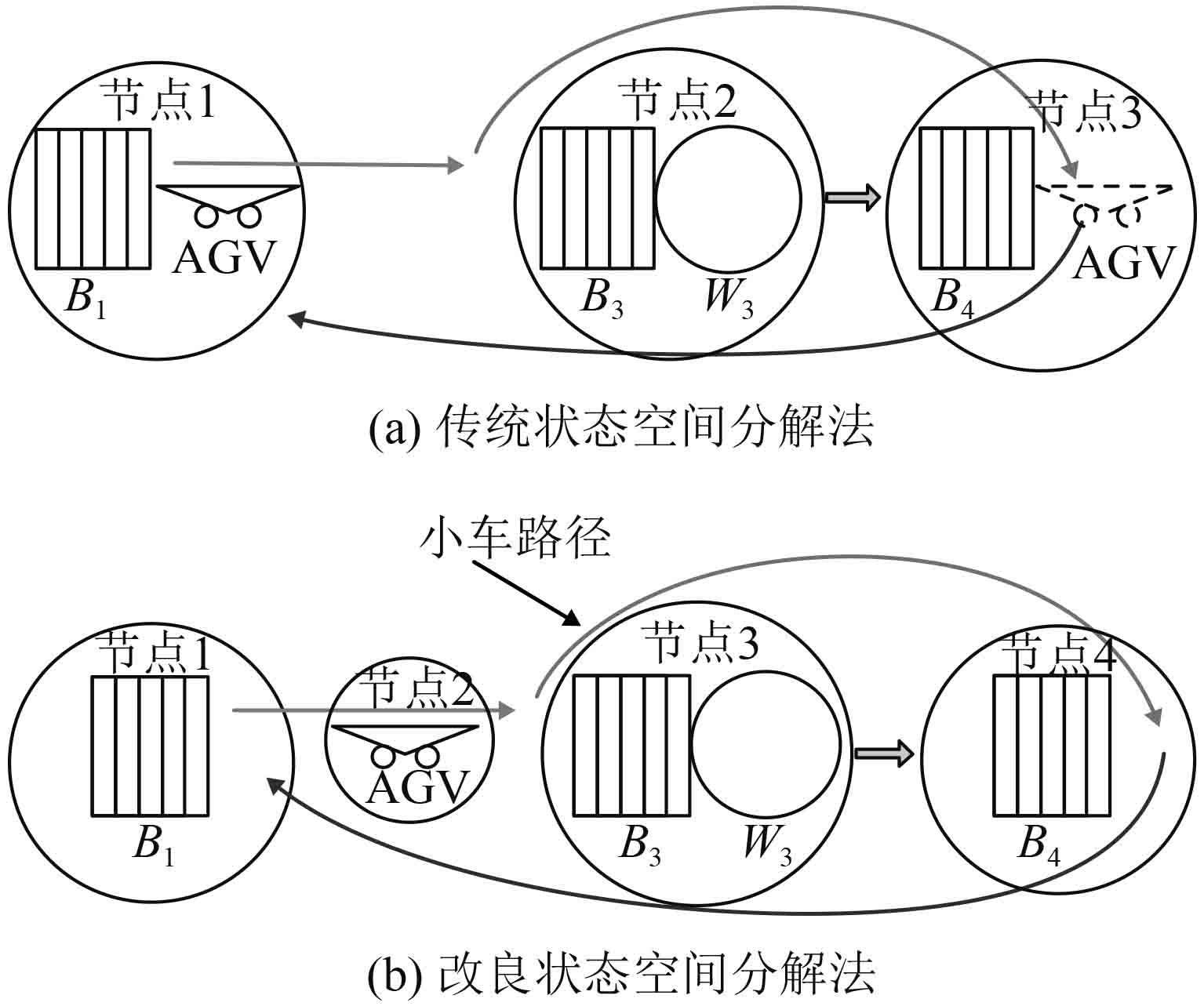
2 基于排队网的性能分析模型 2.1 系统节点划分

由前述可知，小车运输的特点是分段环形运输，在不同的地点与不同的缓存区发生“装卸关系”，且运输批量大小与缓存区工件数有关。依照传统状态空间分解法的节点分解原则进行分解，将缓存区与小车作为一个节点来处理，如图3中(a)图所示，将无法准确地确定节点的稳态状态数量，进而无法建立其准确的状态转移平衡方程。因此，必须将小车与各个环节的缓存独立出来，作为一个单独的节点。基于更新过程的关键更新定理，将小车与B₁、B₃、B₄间的耦合关系用节点间的批量到达速率与批量离开速率变化替代，这样可以准确地确定各节点稳态后的状态数量。具体如图3中(b)图所示，由于工件运回中心仓库后，已离开系统，独立于整个制造系统，因此B₅不作节点划分考虑。

2.2 状态空间分解模型

根据马尔科夫相关理论，多级流水车间的开排队网模型的稳态求解问题总可以转化为连续时间马尔科夫链(continuous-time Markov chain，CTMC)来进行研究，根据各节点的特点分别构建“半独立”的连续时间马尔科夫过程来近似求解。

根据图3(b)划分的节点，将开排队网模型分解成多个单独节点，每个节点中的阻塞概率以及流入、流出速率等参数被用来推导其他相关节点马尔科夫过程状态转移速率平衡方程。虽然每个节点不是完全独立的，但它们都可以视为是“半独立”的，即系统稳态下，某节点处于各个状态的概率基本不变。如当小车节点达到稳态后，近似认为其运输i个工件的概率基本不变，而小车在缓存区装/卸过程可视为一个交错更新过程，此过程只在更新时间点发生且只与小车节点状态有关。所以，通过求解每个节点的状态转移速率平衡方程，即可得到每个节点处于各状态的概率，进一步可以求得系统的性能指标。

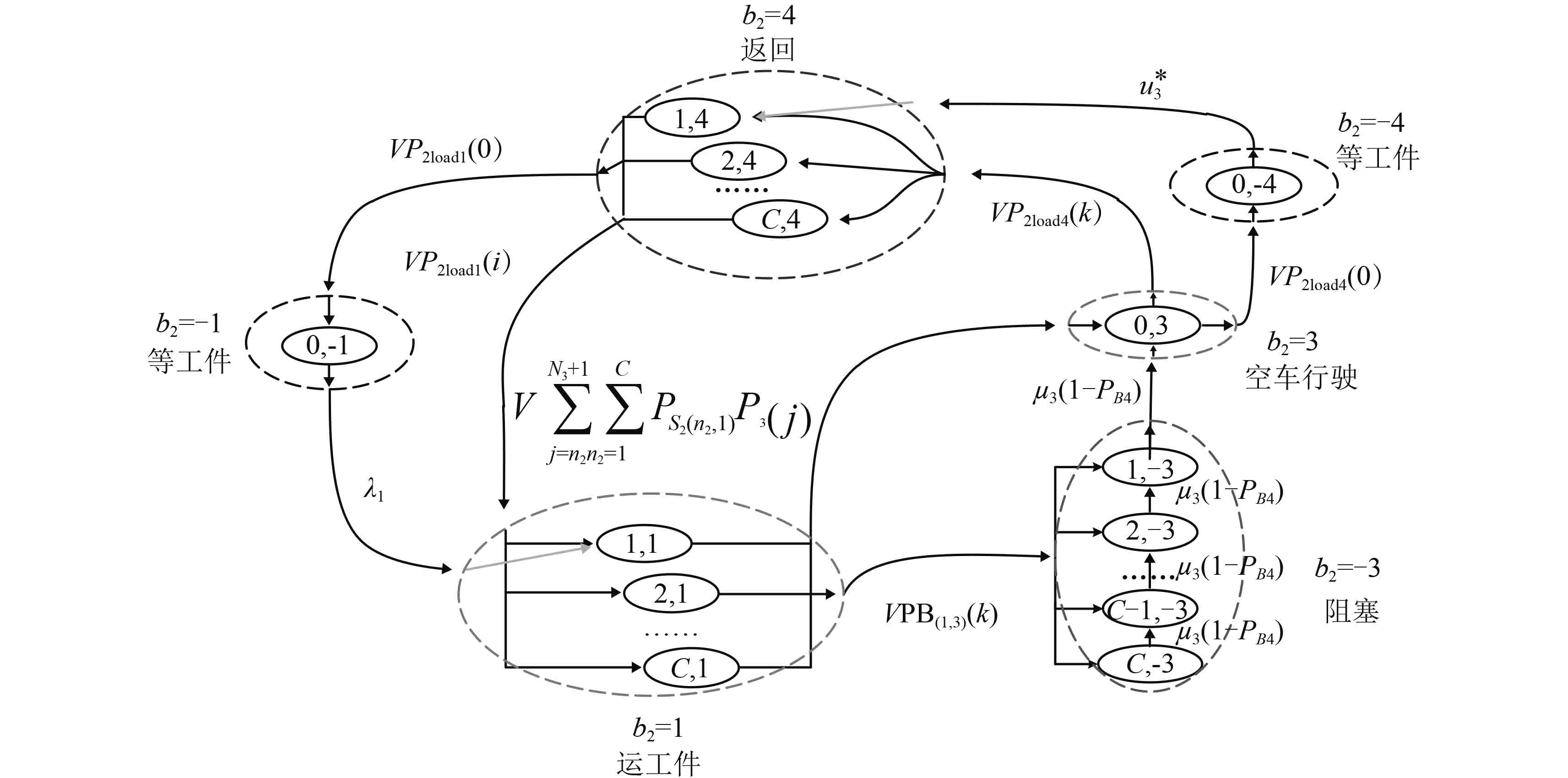
2.2.1 小车节点分析

在图3(b)所示的系统中，小车运输于B₁、B₃、B₄之间，批量装卸，类似于批处理过程。根据模型假设，每一圈运输过程，小车将在B₁处空闲等待、运工件至B₃、B₃处阻塞等待、空车至B₄、B₄处空闲等待、运工件返回这六类状态之间按照一定的规律往复行驶，各类状态及之间的转移如图4所示。

该节点的状态空间为S₂{(n₂,b₂); 0≤n₂≤C;b₂ = –1, 1, –3, 3, –4, 4}，其中，n₂代表小车中的工件数量；b₂代表小车的运行状态(正数表示离开对应的节点；负数表示在对应的节点等待)。小车返回至B₁时，B₁中可能没有工件，小车将等待到至少有1个；设小车到达B₁时，B₁中有i个工件的概率为P₁(i)，其中，N₁为B₁的容量，小车由返回状态(n₂，4)变为等待状态(0，–1)的概率为P₁(0)。小车由等待状态(0，–1)变为运输1个工件状态(1，1)将取决于工件的到达速率λ₁，因此其转化速率为λ₁。小车运输i个工件的概率为P_2load1(i)，当0≤i<C，缓存被清空P_2load1(i)=P₁(i)；当i≥C，小车满载离开，P_2load1(C)= $ \sum\limits_{i = C}^{{N_1}} {{P_1}(i)} $ 。

当小车到达B₃时，分为是否阻塞2种情况，设小车装载数为n₂，B₃当前空位数为j。当j≥n₂，即有足够的空位，小车直接将工件卸下，其状态从运工件状态S₂(n₂，1)直接转化为空车状态S₂(0，3)，转化速率为 $V\sum\limits_{j = {n_2}}^{{N_3} + 1} {\sum\limits_{{n_2} = 1}^C {{P_{{S_2}({n_2},1)}} } } {P_3}(j)$ ，其中，P₃(j)表示节点3空位数为j的概率；当j＜n₂，小车从运输状态S₂(n₂，1)转变为阻塞状态S₂(n₂–j，–3)的速率为VPB₍₁₃₎(j)，其中，PB₍₁₃₎(j)为小车将n₂个工件运达B₃时，B₃的剩余空位为j(0≤j＜C)的概率。由于W₃不断加工使得B₃出现新的空位，小车上的工件数不断减少，其转换速率为μ₃(1–P_B4)，P_B4表示B₄将加工中心堵塞的概率。当小车上工件卸完后，空车运行至B₄，状态转化为S₂(0，3)。小车到达B₄类似于到达B₁，可同样分析出其各个状态的转移速率，此处不再赘述。

小车整个运行过程，是一个再生过程。当系统稳态时，可以得到其处于各状态的概率P_S2(b₂)。又根据模型假设：B₁至B₃、B₃至B₄以及B₄至B₁这3个过程的平均速率均为V，可得处于这3类状态的平均时间T₁=T₃=T₄=V^–1。根据更新过程相关定理可以得到小车每个循环中处于–1，–3，–4状态的平均时间为 ${T_L} = \frac{1}{V} \times \displaystyle\frac{{{P_{{S_2}(L)}}}}{{{P_{{S_2}(1)}}}}$ ，L= –1，–3，–4。

2.2.2 中心仓库节点(B₁)分析

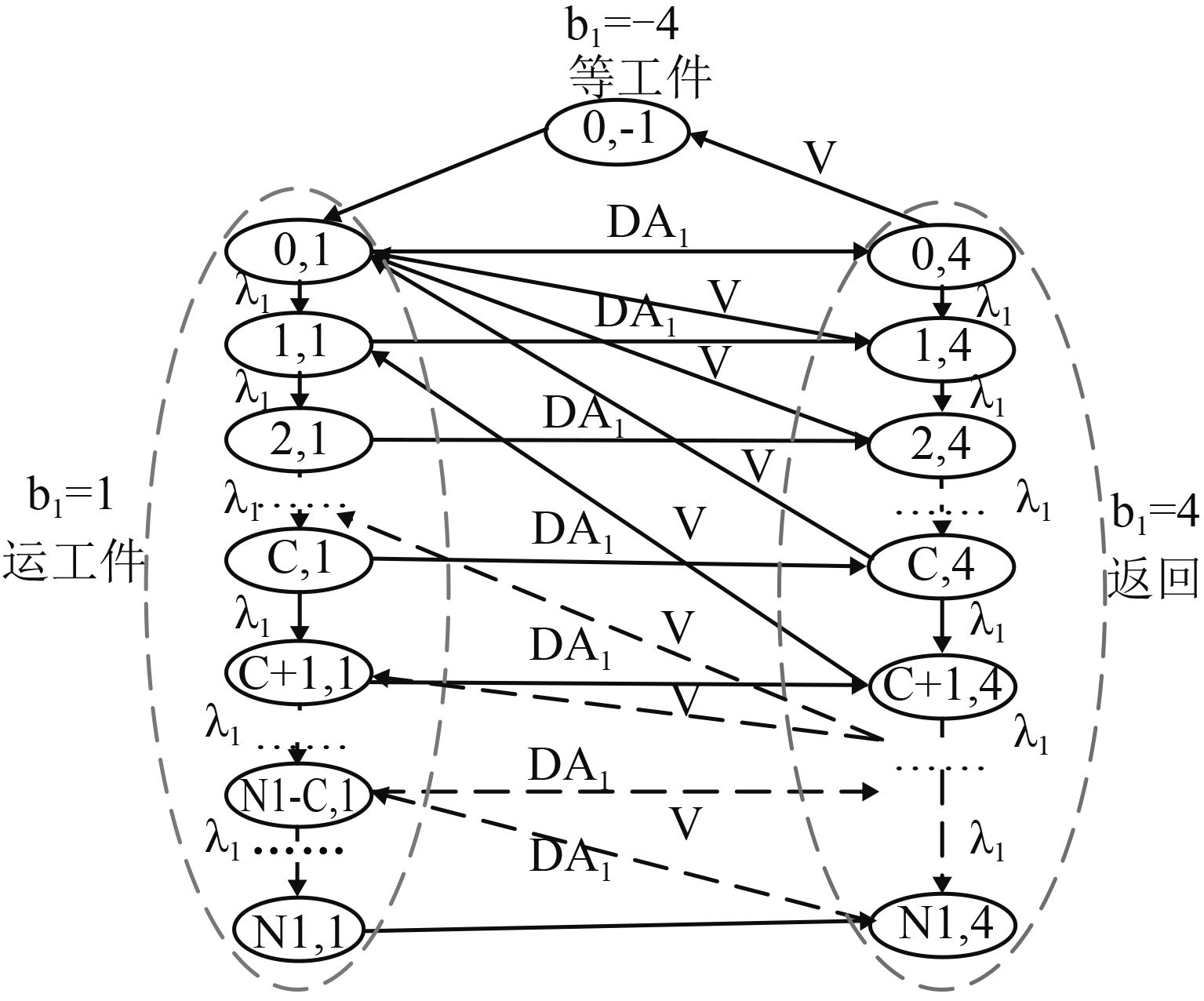
对节点1而言，订单按照随机分布到达，然后被小车运离，其过程可描述为单个到达、批量离开。相对于工件到达B₁时间间隔而言，从小车离开B₁到再次回到B₁这段时间，通常会有多个工件到达B₁，所以B₁工件数量是单调非减的。通过拆分状态，建立如图5所示的状态空间。

设节点1的状态空间为S₁{(n₁,b₁); 1≤n₁≤N₁;b₁= –1, 1, 4}，其中，n₁代表B₁中的工件数量；b₁代表小车的运行状态：–1代表在B₁处等待(对应S₂中b₂=–1)，1代表处于从B₁行驶至B₄途中(对应S₂中b₂=1，–3，3，–4)，4代表从B₄返回中心仓库(对应S₂中b₂=4)。节点1的状态空间总共有(N₁+1)×2+1个状态。图中λ₁是节点的流入速率，DA₁是小车从B₁前往B₃、在B₃阻塞等待、从B₃至B₄和在B₄空闲等待这4个过程的平均速率，满足 ${\rm{D}}{{\rm{A}}_1} = {({T_1} + {T_{ - 3}} + {T_3} + {T_{ - 4}})^{ - 1}}$ ，速率V由题设给出。

2.2.3 加工中心节点(B₃,W₃)分析

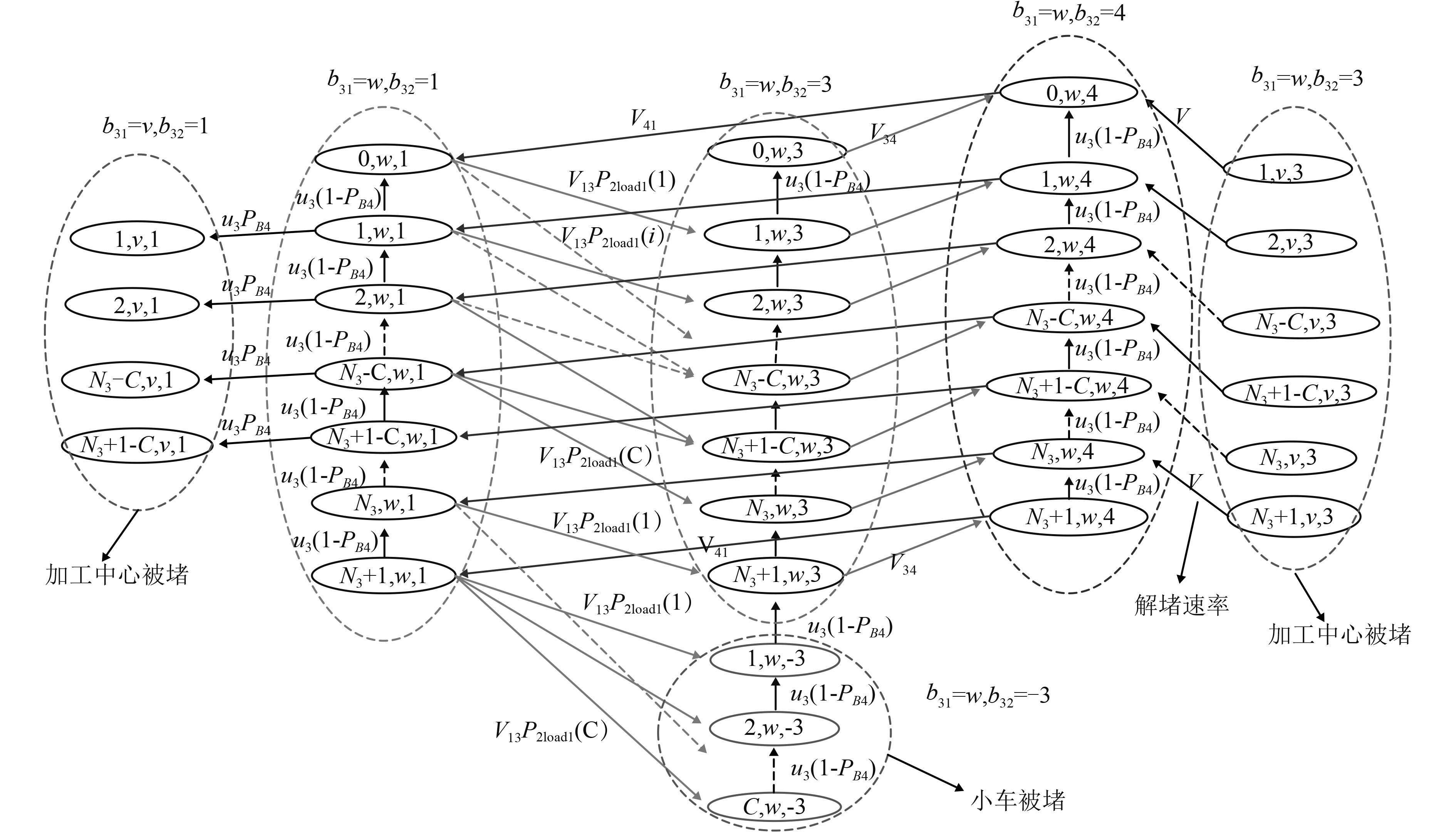
节点3是加工中心节点，既要考虑小车状态，又要考虑自身是否被后节点阻塞。设状态空间S₃{(n₃,b₃₁,b₃₂); 0≤n₃≤N₃+1;b₃₁=w,v;b₃₂=1, –3, 3, 4}。其中，当小车到达B₃时，如果一次性卸载，n₃表示节点3工件数量，如果阻塞等待，则n₃表示小车上剩余工件数量。b₃₁表示节点3是否被B₄阻塞，b₃₂表示小车状态。b₃₁=w表示处于正常加工状态(包括空闲)，没有被堵，而b₃₁=v表示被堵。b₃₂=1, 3, 4分别表示小车从B₁至B₃、从B₃至B₄、从B₄返回三类状态(分别对应S₂中b₂=1, 3, 4)；b₃₂= –3表示小车阻塞等待。图6为节点3部分状态分布图，共有6(N₃+1)+3–C个状态。图中V₁₃表示小车从B₁行驶至B₃和在B₃处阻塞等待的平均速率。小车每次送达个数的分布 ${P_{2{\rm{load}}1}}(i) = {P_{{S_2}\left( {i,1} \right)}}/{A_i},1 {\text{≤}} i {\text{≤}} C$ ，其中 ${A_i} = \sum\limits_{{n_i} = 1}^C {{P_{{S_2}\left( {{n_i},1} \right)}}} $ 。

2.2.4 完工工件缓存节点(B₄)分析

节点4的流入速率为节点3的流出速率μ₃^*，其分析与节点1相同，此处不再赘述。

2.3 各节点状态平衡方程与求解方法

由于各节点所有状态都是常返的，离开某状态的速率与进入该状态的速率相等。因此可以根据上述状态转移图列出对应的状态转移平衡方程组。如节点2状态S₂{(0，–1)}的平衡方程为 ${P_{{S_2}\left( {0, - 1} \right)}}{\lambda _1} = $ $\sum\limits_{k = 1}^C {{P_{{S_2}\left( {k,4} \right)}}} \times V{P_1}\left( 0 \right)$ ，其他节点的每个状态的平衡方程亦可类似列出。根据状态平衡方程组，各方程系数组成相应的稀疏矩阵，可用Gauss-Seidel迭代法^[14]求得各节点状态的稳态概率。此外，文献[15]证明了连续时间马尔可夫过程状态平衡方程在迭代过程中的收敛性，因此在迭代过程收敛后，最终可获得系统各状态的稳态概率值，进一步可计算系统各性能指标值。

2.4 系统性能指标计算方法

由上文状态空间法的平衡方程可以得到的各状态稳态概率 ${P_{{S_i}({n_i},{b_i})}}$ 或 ${P_{{S_i}({n_i},{b_i},{b_j})}}$ 。由于工件由小车搬运离开系统，因此系统的平均产出率取决于小车处于返回状态 ${P_{{S_2}({n_2},4)}}$ 的概率分布。对应性能指标可用以下公式求得。

平均产出率为 ${\rm{Output}} = \mathop \sum \limits_{{n_2} = 1}^C {P_{{S_2}\left( {{n_2},4} \right)}} {n_2}$，

平均队长为 ${\text{WIP}} = \mathop \sum \limits_{i = 1}^4 {N_i}$。

3 算例与系统性能分析 3.1 仿真模型

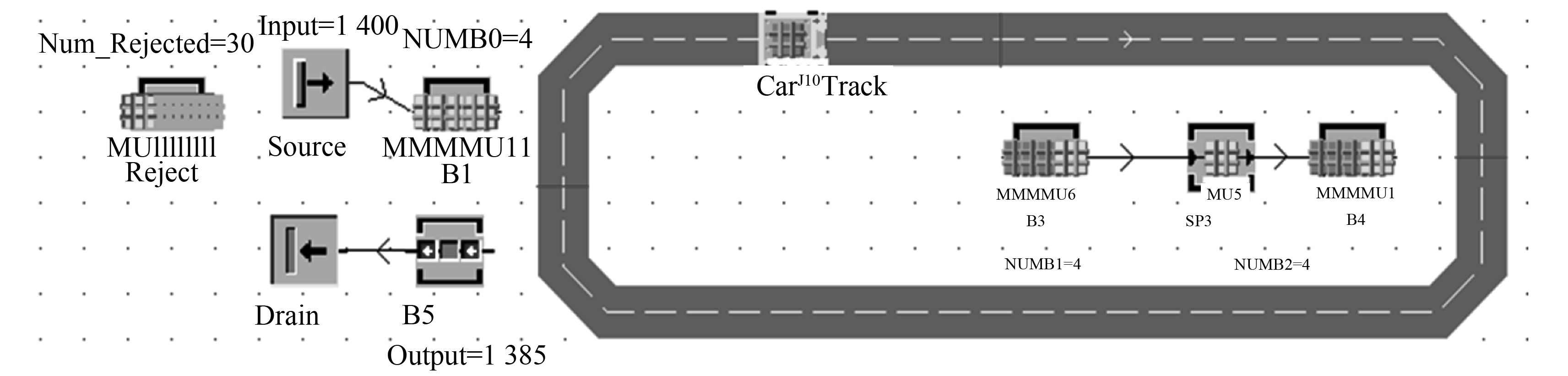
图7为在Tecnomatix Plant Simulation 8.2上建立对应的仿真模型，用来验证改良状态空间分解法的有效性。基于Monte Carlo仿真理论，在大样本的条件下，构造统计估计量并计算采集的数据样本，每次实验1 000 d并取系统稳态后的数据进行统计(每次实验样本容量约为10⁵)，所有仿真结果取30次实验的平均值。

3.2 实验变量

为了保证车间生产的顺利进行，通常情况下交给车间的生产任务应该略小于车间的产能，即输入速率λ与处理速率μ的比值略小于1，一般0.8≤(λ:μ)≤1。

小车作为运输工具，其运输速率V与最大装载容量C将直接影响车间的生产状况，若当量运输能力(V×C)过大，将导致小车利用率低，浪费资源；反之，将导致生产线拥堵严重，阻碍生产。

各级缓存大小直接决定系统在制品数，缓存越大，将使得大量的工件处于排队等候状态，其在系统中停留的时间变长，从而导致生产周期变长；反之，缓存越小，工件容易阻塞，使得生产能力下降。

3.3 实验结果及系统性能分析

根据上节分析，以下将通过改变以上参数来验证状态空间分解法的有效性，如表1所示。其中，S组是参照单元；A组是研究工件到达速率对系统影响；B组是研究小车的速率对系统影响；C组是研究小车容量对系统影响；D组是保持小车的当量运输能力不变，研究不同速率与容量对系统影响；E组是研究各级缓存大小对系统的影响。

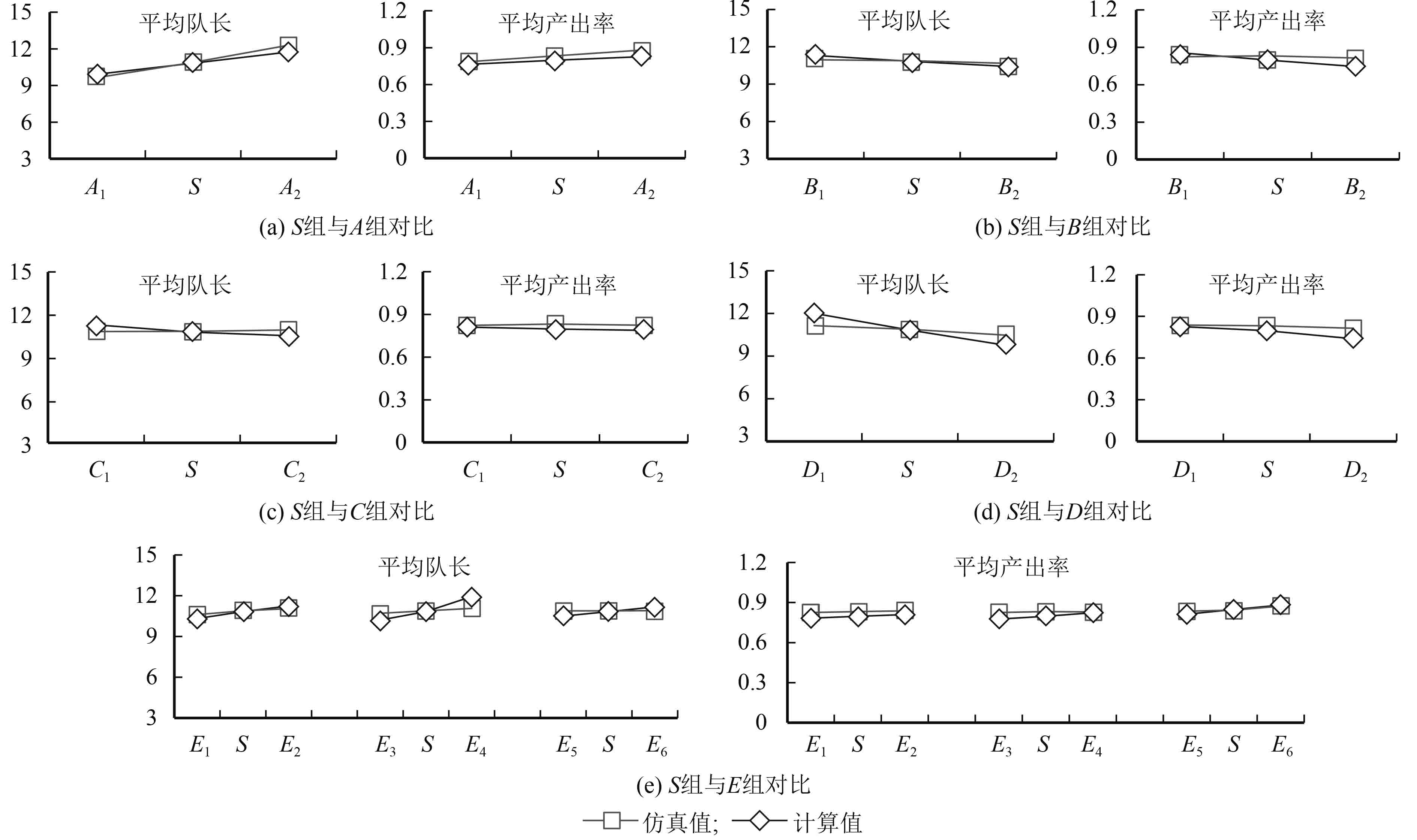
各组实验算例求解结果如表1与图8所示，表中∆(%)为近似计算结果与仿真结果的偏差百分比。总体来看，计算出的WIP的误差大部分在3%~7%左右，最高误差为7.80%；产出率误差大部分在2%~6%，最高误差为9.18%，误差属于可接受范围。

通过分析表1数据与图8规律曲线，可以得到不同参数变化对系统性能指标变化影响如下。

1)S组与A组对比可知，随着输入速率的增大，系统的在制品数量与产出率都随之增大。由于单位时间到达的工件数量增加，而加工中心与小车的处理速率没变，因此停留在各缓存的工件数量增加；产出率主要取决于小车返回过程(b₂=4)，由于节点4缓存工件数量增加，小车返回过程装载的工件数量平均值增大，因此产出率增大。

2)S组与B组对比可知，单独增加小车速率，系统的在制品数量减少，而产出率减小了。由于小车运输速率增大了，因此在各级缓存等待的工件数量减少，小车访问各个缓存的时间间隔减小，运载的个数的期望值也减小了，从而导致产出率减小。

3)S组与C组对比可知，改变小车的运载容量，系统的在制品数量与产出率变化非常小。这是因为系统的输入与处理速率没变，在小车运力足够的情况下，由于各级缓存基本不变，因此小车每次运输的工件数量均值并没有实质性的变化，从而产出率基本不变。

4)S组与D组对比可知，保持小车当量运输能力不变，小车速率增大，运载容量减小，使得系统在制品数量减少，产出率也减小。随着小车运载速率增大，工件被更快地运离了系统，因此在制品数量减少；受加工中心的产能限制，小车速率的增加并不一定使得缓存B₄工件数增加，而小车访问B₄的时间间隔减小，从而小车在返回过程运载工件的平均值减小，从而导致产出率下降。从图8(b)、(c)、(d)3组结果可以看出，系统产出率主要受小车速率的影响。

5)S组与E组对比可知，随着各级缓存容量增加，系统在制品数量跟产出率都随之增大。缓存容量增大，使得在缓存中排队等候的工件数增加。对于缓存B₄，由于小车从其中运载工件返回的速率直接影响着产出率，随着B₄缓存增大，小车每个返回过程运载工件的平均值增大，因此增大B₄对于产出率的提高较其他缓存而言更加明显。

4 结束语

针对带环形路径AMHU的制造系统，建立排队网模型，并通过改良传统状态空间分解法对模型进行近似求解。由于小车与各节点之间的耦合关系，按照传统状态空间分解法无法确定各节点准确的状态数量，为此，将小车独立出来进行分析，而加工单元既要考虑小车卸载受阻，又要考虑自身堵塞，通过定义变量b₃₁、b₃₂分别描述小车状态与加工单元状态，并对制造系统进行仿真，对比验证了改良的状态空间分解法具有较高的精度。为进一步研究带有AMHU的制造系统以及同类制造系统的系统设计或资源优化问题提供参考。