2. 机务处,四川 广汉 618307
2. Maintemance Office, Civil Aviation Flight University of China, Guanghan 618307, China
通用教练机机队配置优化的目的在于准确测算教练机机队中飞机的数量及优化机型的构成比例,以此满足飞行航校未来飞行训练培训市场的规模,并实现机队运营效益的最大化。近年来,随着我国民航运输业的迅猛发展,航空驾驶员培训市场规模也在不断增长。然而,紧缺的航空驾驶员飞行训练配套资源,尤其是训练空域资源的相对短缺,已经无法与日益增长的航空驾驶员培训市场相匹配。为了缓解这一矛盾,多训练基地的网络化训练已成为飞行航校扩大培训规模的重要手段。所谓网络化训练,是指打破传统航空驾驶员培训在单一训练基地实现多个执照等级一体化培训的模式,允许航空驾驶学员执照等级训练任务在多个训练基地之间流动,并使整个飞行训练过程形成一种资源共享、优势互补的紧密训练网络。而合理规划教练机机队的规模与结构(飞机数量与机型构成比例),并将其科学地部署到各个训练基地,又是关系到飞行航校能否充分发挥出网络化训练优势的关键。因此,研究网络化训练下通用教练机机队配置优化方法,对于扩大飞行航校培训规模,降低飞行训练成本,以及提高飞行训练效率都具有重要意义。近年来,关于通用教练机机队配置问题的研究成果较少。田静等[1]探讨了单训练基地下通用教练机机队优化配置问题,并通过灵敏度分析指出了影响教练机优化配置与运营成本的主要影响因素,但没有进一步讨论多训练基地网络化训练下的教练机机队优化配置问题。关于多基地的机队配置优化问题的讨论更多的集中于商用大型运输类飞机的微观机队规划层面[2-3]。然而,该类问题关注的重点在于航线/航班上的旅客需求与机型座级在技术经济层面的适应性[4-7],目标在于获取合理的机队规模与结构以实现机队运营利润(或成本)的最大化(或最小化);而通用教练机机队配置优化更多地关注于航空驾驶员培训任务在不同教练机机型上的流动过程,目标在于以最少的机队运营成本完成未来航空驾驶员培训市场上所有培训任务要求。两者之间的显著差异使得大型商用运输类飞机机队规划方法无法直接用于测算通用教练机机队的规模与结构。
鉴于此,本文首先分析了网络化训练过程中航空驾驶员执照训练任务路径选择对于通用教练机机队配置决策的影响;然后,综合考虑航空驾驶学员流动平衡限制、通用教练机机队可用飞行时间限制及其基地最少投放飞机数限制等因素,构建以机队训练成本最小化的机队配置优化数学模型;最后,通过与目前普遍采用的航空驾驶员训练模式相比较说明本文方法的优劣。
1 问题提出根据《民用航空器驾驶员和地面教员合格审定规则(CCAR-61-R4)》[8]规定,飞行航校在培养航线驾驶员时必须按照私用驾驶员执照、商用驾驶员执照和航线驾驶员执照3个执照等级逐一进行训练。而依次完成3个执照等级又必须要满足《民用航空器驾驶员学校合格审定规则(CCAR-141)》[9]规定中包含的关于航空驾驶员培训训练科目的最低实施要求。为了满足上述法规要求,飞行航校会根据教练机的技术经济性能特点选择由不同型别等级教练机组成飞行训练机队。通常而言,通用教练机机队由单发(初教)、双发(中教)和高性能教练机(高教)3种型别等级飞机组成。为了完成航空驾驶员培训任务,依次进行的3个执照等级训练过程必须在相应的教练机上完成。
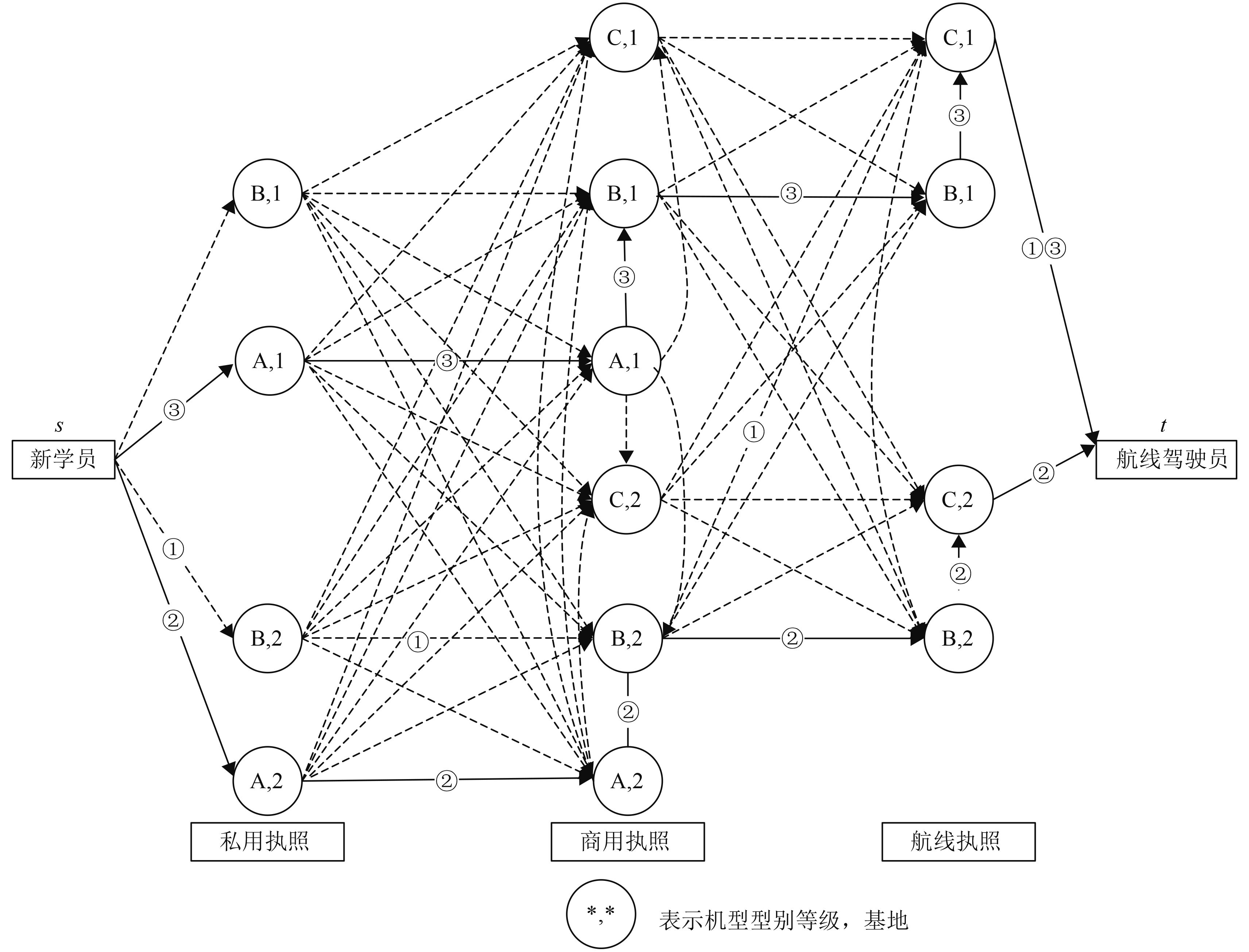
图1给出了网络化训练下两基地航空驾驶员培训任务流程。其中,“实线”给出了目前飞行航校所普遍采用的训练任务路径;“虚线”则给出了潜在可行的训练任务路径。
|
图 1 两基地网络化训练下的航空驾驶员培训流程 Fig. 1 training process for aviation drivers under network training of two operating bases |
可以发现,多阶段执照等级训练任务在教练机机型上的流动路径不同,航空驾驶员训练所使用机型飞机的运营成本是不完全相同的。例如,训练路径②上私照阶段利用的是初级教练机A(即“私照单发”训练);而训练路径①上利用的是中级教练机B(即“私照双发”训练),显然由于机型技术经济性能的差异性,两种方案的机队运营成本是不同的。另外,不同任务路径所产生的改装训练成本也是不完全相同的,例如,训练路径②上需要进行“初教-中教、中教-高教”两次改装训练;而训练路径①上只需要“中教-高教”一次改装训练。更为重要的是,不同训练任务路径选择所产生的各类教练机机型及其所需飞机数,以及基地型别等级机型的部署计划也不尽相同。例如,训练路径①只需“中教”、“高教”教练机;而训练路径②需要“初教”、“中教”、“高教”3种教练机,且所选择的2种训练路径需要在基地2部署“初教”、“中教”、“高教”3种教练机,但在基地1仅需要部署“高教”教练机。可以说,2种不同的任务路径产生了不同的机队所有权成本,而且还会导致不同的基地机型部署计划方案。可以看出,教练机配置优化问题受到训练任务路径选择的深刻影响。本文试图针对多训练基地网络化训练模式下的通用教练机机队配置问题,以机队训练总成本最小化为目标函数,以训练任务路径优化选择为决策手段,研究教练机机队配置及其基地机型的部署优化方法,旨在为飞行航校开展网络化训练下的通用教练机机队配置问题提供一种科学的决策方法。
2 基于带权有向图的数学模型为了便于问题说明,本文作出如下假设。
1) 暂不考虑各个执照等级阶段的航空驾驶学员淘汰问题,假设流入某个执照阶段的学员总人数与流出该执照阶段的总学员人数相等。
2) 考虑到商用执照阶段可以分为“单发商照”阶段(“初教”执飞)与“多发商照”阶段(“中教”或“高教”执飞);航线运输执照阶段可以分为“小双发航线运输执照(“中教”执飞)”阶段或“高性能多发航线运输执照(“高教”执飞)”阶段,因此假设在“单发商照”与“小双发航线运输执照”阶段后航空驾驶学员可以在不同训练基地之间流动,其它执照阶段均视为一个整体,即在未完成完整的一个执照阶段前不允许航空驾驶学员在不同训练基地之间流动。
3) 暂不考虑不同基地之间航空驾驶学员的流动管理成本。
在此基础上,将多训练基地下网络化训练的培训流程抽象为一个带权的有向图(G,V,E,C)。具体构造方法如下。
1) 记I、J、K分别表示执照等级集合、训练基地集合和教练机机型(型别等级)集合,则带权有向图的顶点可以记为V={(i,j,k)|i∈I,j∈J,k∈K}。
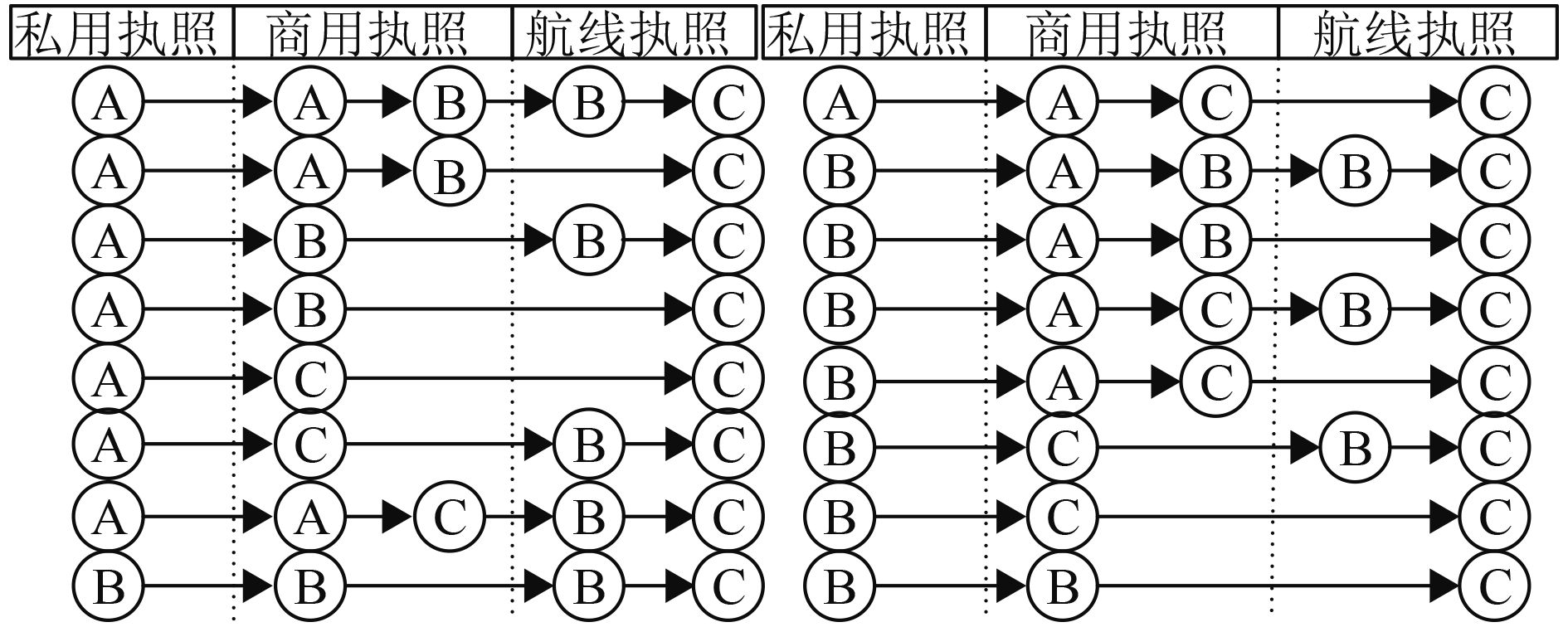
2) 记有向弧集合E={(m,n)|m,n∈V,m≠n},且带权有向图G中的有向弧必须满足执照等级任务与机型型别等级指派,以及任务流经机型型别等级的合法性,即仅在图2所示的任务路径中的有向弧才是符合法规要求的,并以此确定顶点之间的相邻关系。
|
图 2 所有潜在任务路径下的合法有向弧 Fig. 2 legal directed arcs in all potential assignment paths |
3) 添加带权有向图的首节点s,且与私照训练阶段的所有可用机型型别等级相连,并添加相应的尾节点t,且与航线训练阶段的所有合法机型型别等级相连,如图1所示。
4) 对于带权有向图上的任一有向弧e,根据该有向弧指向顶点n所属的执照阶段i,以及所采用的任务训练机型型别等级k,给出法规规定训练时间
需要注意的是,所有与尾节点相连的有向弧的权重以及相应的总训练时间均为0。
2.1 目标函数在上述带权有向图的基础上,以机队训练成本最小化为目标函数的通用教练机机队配置优化数学模型如式(1)所示。
| $\quad\quad \min {\kern 1pt} {\kern 1pt} f = \sum\limits_{\left( {m,n} \right) \in E} {{c_{mn}}{x_{mn}}} + \sum\limits_{j \in J} {\sum\limits_{k \in K} {{\mu _k}{z_{jk}}} }{{\text{。}}}$ | (1) |
其中,xmn 表示流经有向弧(m,n)的航空驾驶学员人数(单位:人次);μk 表示单架教练机机型k飞机的所有权成本(单位:万元/架);zjk 表示教练机机型k飞机在训练基地j(j∈J)部署的飞机数量(单位:架)。
2.2 约束条件1) 航空驾驶学员总人数限制。从首节点s流出到所有节点上的航空驾驶学员人数之和等于整个训练周期内航空驾驶学员的总人数,如式(2)所示。另外,从所有节点上流入尾节点t的航空驾驶学员人数之和等于整个训练周期内航空驾驶学员的总人数,如式(3)所示。
| $\quad\quad \sum\limits_{n \in {\rm{adj}}\left( s \right)} {{x_{sn}}} = T{{\text{,}}}$ | (2) |
| $\quad\quad \sum\limits_{m:t \in {\rm{adj}}\left( m \right)} {{x_{mt}}} = T{{\text{。}}}$ | (3) |
其中,T表示一个训练周期内航空驾驶学员的总人数(单位:人次);adj(·)表示与节点“·”相连接的有向弧。
2) 航空驾驶学员流平衡条件。流入节点m的航空驾驶员人数等于流出该节点的航空驾驶员人数,如式(4)所示。
| $\quad\quad \sum\limits_{m:n \in {\rm{adj}}\left( m \right)} {{x_{mn}}} = \sum\limits_{m \in {\rm{adj}}\left( n \right)} {{x_{nm}}} ,\forall n \in V{{\text{。}}}$ | (4) |
3) 通用教练机机队最大可用飞行时间限制。由于受到法规规定的航空器持续适航限制、飞行训练管理模式限制,以及空域容量限制等因素的影响,在任一训练基地,每一种特定型别等级机型机队的可用飞行时间,以及整体教练机机队的可用飞行时间都是有限的,因此,相应型别等级机型机队的飞行时间不能超过该机队可提供的最大可用飞行时间限制,且整体机队的飞行时间同样也不能超过其可利用的最大飞行时间限制,如式(5)和式(6)所示。
| $\begin{split}\sum\limits_{\left( {m,n} \right) \in E} {{b_{mn}}{x_{mn}}} {\text{≤}} \sum\limits_{j \in J} {{a_{jk}}{z_{jk}}}, \forall j \in J,k \in K,n \in \left\{ {\left( {i,j,k} \right)|\forall i \in I} \right\}{{\text{;}}}\end{split}$ | (5) |
| $\begin{split}\sum\limits_{\left( {m,n} \right) \in E} {{b_{mn}}{x_{mn}}} {\text{≤}} {F_j},\forall j \in J,n \in \left\{ {\left( {i,j,k} \right)|\forall i \in I,k \in K} \right\}{{\text{。}}}\end{split}$ | (6) |
其中,ajk 表示一个训练周期内训练基地j上部署的型别等级机型k飞机的期望利用率(单位:h);Fj 表示一个训练周期内训练基地j上部署的通用教练机机队整体的可用飞行时间(单位:h)。
4) 特定型别等级机型机队在训练基地最少投放飞机数限制。考虑到某型别等级机型机队的飞机数在某一训练基地投放过少会导致维修成本增加、航材备件管理复杂化等问题,因此必须为训练基地设置一个特定型别等级机型机队飞机的最少投放数,如式(7)和式(8)所示。
| $\quad\quad {n_{jk}} - {z_{jk}} {\text{≤}} \left( {1 - {y_{jk}}} \right)M,\forall j \in J,k \in K{{\text{;}}}$ | (7) |
| $\quad\quad {z_{jk}} {\text{≤}} {y_{jk}}M,\forall j \in J,k \in K{{\text{。}}}$ | (8) |
其中,yjk 为0-1型变量,若训练基地j投放型别等级机型k飞机时为1,否则为0;njk 表示教练机机型k飞机在训练基地j(j∈J)被部署的最少飞机数量(单位:架);M为正的无穷大数。
5) 变量类型与取值范围。
| $\quad\quad {x_{ijk}},{z_{jk}},{\mathop{\rm int}} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \forall i \in I,j \in J,k \in K{{\text{,}}}$ | (9) |
| $\quad\quad {y_{jk}} \in \left\{ {0,1} \right\},\forall j \in J,k \in K{{\text{。}}}$ | (10) |
某航空驾驶学校拥有3个训练基地,且一个训练周期培养航线驾驶员1 000名,3种执照等级阶段所需培训时间如表1所示。该飞行航校所采用的通用教练机机型型别等级分别为初教(A),中教(B)与高教(C)。不同机型之间的改装训练时间、3个训练基地上的各类型别等级机型的飞机利用率与其它相关运营统计信息如表2和表3所示。
| 表 1 执照等级训练时间 Tab. 1 training hours of each License grade |
| 表 2 不同机型之间的改装训练时间 Tab. 2 modification hours between different aircraft types |
| 表 3 型别等级机型在训练基地的飞机利用率与其它相关运营统计信息 Tab. 3 aircraft utilization rate and other operation-related information for each aircraft-type-rank by training base |
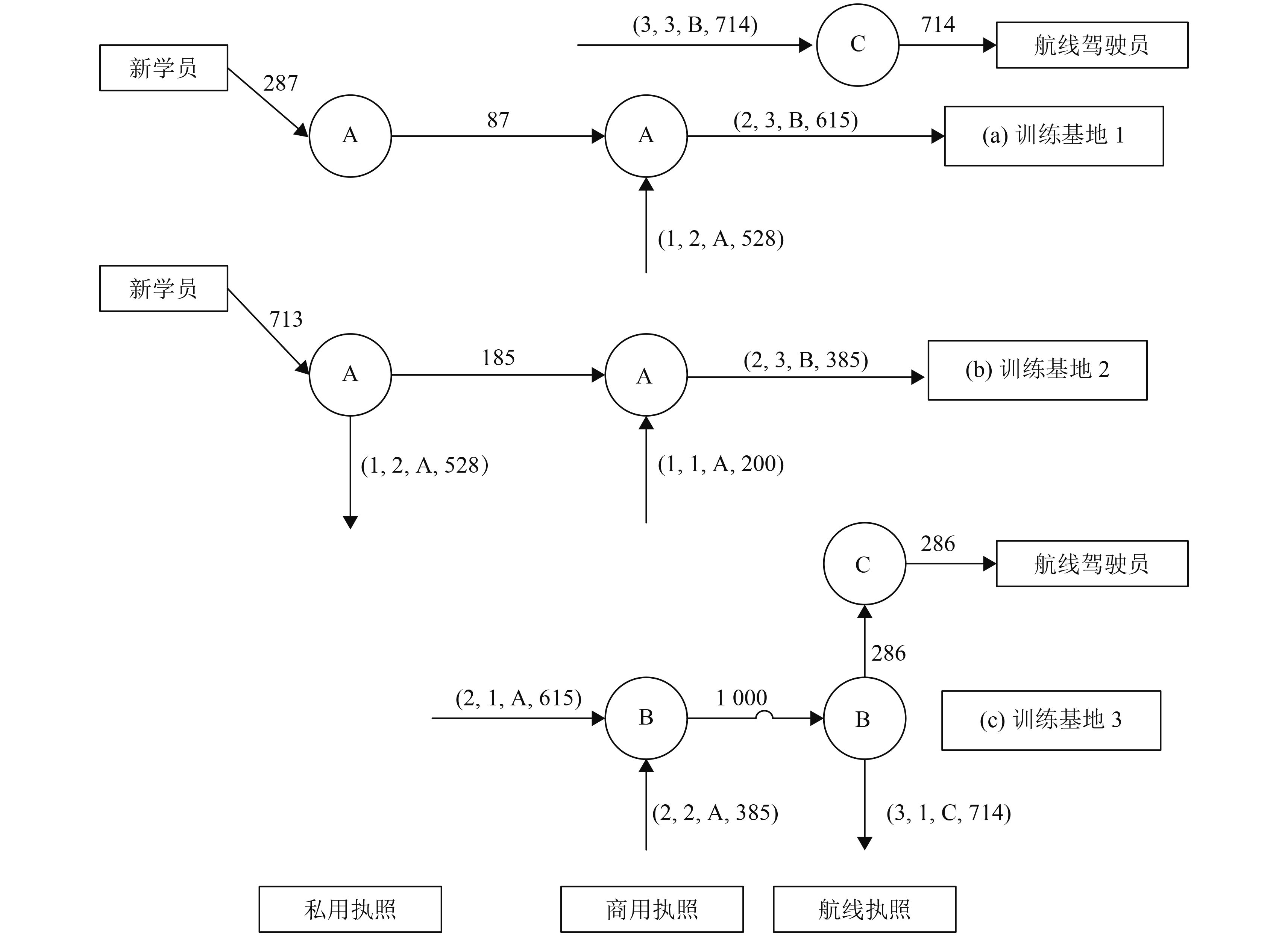
根据带权有向图的构造方法,给出一个包含23顶点,126条有向弧的带权有向图。利用Matlab中的优化工具箱YALMIP进行计算,得出的各训练基地的人员流转情况如图3所示。
|
图 3 训练基地学员流转示意图 Fig. 3 pilot flowing diagram between different training bases (*, *, *, *)表示“执照阶段,训练基地,机型,流转人数” |
可以发现,与目前飞行航校普遍采用的训练任务路径(即采用A-A-B-B-C任务路径)相比较,图3中训练基地1配置的机型为初教(A)和高教(C);训练基地2配置的机型为初教(A);训练基地3配置的机型为中教(B)和高教(C)。因此,允许学员在不同训练基地之间流转的网络化训练模式有效的减少了教练机机型在基地配置的数量,并降低了教练机机队管理的复杂性。得出的各训练基地的机型飞机数量及其费用情况如表4所示。
| 表 4 训练基地配置的各机型飞机数量及其费用 Tab. 4 number of aircraft of different types deploying to each training base and its corresponding cost |
可以发现,优化后机队中飞机的总数量减少了24架,机队训练成本相应减少了0.09亿元(2.7%)。将该成本费用折合到机队的整个使用周期内(10~15年),那么大约能够节省0.9~1.35亿元,因此可以显著的降低飞行航校的训练费用。
4 结语本文针对飞行航校的多训练基地、多阶段训练任务的网络化飞行训练模式,以降低机队训练成本为目标函数,将该飞行训练模式下的飞行训练过程抽象为一种带权的有向图。基于此,通过综合考虑航空驾驶学员总人数限制、带权有向图中节点的流平衡限制、机队可用飞行时间限制等因素,建立起了一种基于带权有向图的通用教练机机队配置优化数学模型。在案例中,通过与飞行航校普遍所采用的训练模式下的机队配置优化问题进行比较,发现通过本文所提方法优化飞行训练机型型别等级与任务指派及其路径后,能够减少训练基地机型的配置数量,并降低网络化训练下通用教练机机队的训练成本。该方法可以为飞行航校在网络化训练下合理安排训练任务、科学配置教练机机队提供一种量化的参考。未来可以进一步细分各类型别等级的机型种类,开展多训练基地、多执照等级、多机型通用教练机机队配置优化方法的研究,进而为更为复杂的飞行训练过程提供科学的决策方法。
| [1] |
田静, 赵彦军, 余芬. 通用教练机机队优化配置[J].
交通运输系统工程与信息, 2014, 14(2): 108-193.
TIAN Jing, ZHAO Yanjun, YU Fen. Optimal allocation of general trainer fleet[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(2): 108-193. |
| [2] | BELOBABA P, ODONI A, BARNHART C. The global airline industry [M]. Wiley: West Sussex, 2009. |
| [3] | 朱金福. 航空运输规划[M]. 西安: 西北工业大学出版社, 2009. |
| [4] |
段晓江, 冯允成. 启发式民用飞机机队规划[J].
北京航空航天大学学报, 1996, 22(4): 504-508.
DUAN Xiaojiang, FENG Yuncheng. Efficient heuristic algorithm to airline fleet planning[J]. Journal of Beijing University of Aeronautics and Astronautics, 1996, 22(4): 504-508. |
| [5] | DOZIC S, KALIC M. Three-stage airline fleet planning model[J]. Journals of Air Transport Management, 2015, 46(1): 30-39. |
| [6] |
汪瑜, 朱金福, 葛伟. 随机需求航线网络效应下机队鲁棒优化方法[J].
西南交通大学学报, 2014, 49(4): 727-733.
WANG Yu, ZHU Jinfu, GE Wei. Airline fleet robust optimization approach under stochastic demand with route network effects[J]. Journal of Southwest Jiaotong University, 2014, 49(4): 727-733. |
| [7] |
汪瑜, 孙宏, 朱金福. 基于时间区间内航线机型优化分配的机队规划方法[J].
系统工程理论与实践, 2015, 35(1): 963-970.
WANG Yu, SUN Hong, ZHU Jinfu. Airline fleet planning approach based on optimized allocation between routes and aircraft types within time intervals[J]. Systems Engineering- Theory and Practice, 2015, 35(1): 963-970. |
| [8] | 中国民用航空局. 民用航空器驾驶员和地面教员合格审定规则(CCAR-61-R4) [Z]. 2014. http://industry.wanfangdata.com.cn/hk/Detail/Claw?id=Claw_G000223261 |
| [9] | 中国民用航空局. 民用航空器驾驶员学校合格审定规则(CCAR-141) [Z]. 2004. http://www.geocities.ws/shuchuan/czfg/showart_homecbae.html |
 2017, Vol. 20
2017, Vol. 20