2. 江西财经大学 工商管理学院,江西 南昌 330013
2. School of Business Adminstration, Jiangxi University of Finance and Economics, Nanchang 330013, China
我国正快速进入人口老龄化阶段。随着老龄人口比重的上升,传统的医疗护理模式将会难以满足老年人日益扩大的医疗需求,而家庭医疗护理(home health care,HHC)这个新兴产业正是解决这一问题的一个重要方案。在家庭医疗护理中,医护人员依据与客户约定好的日期和时间,带上必要的医疗设备上门提供医疗检查、康复护理等服务[1],这种模式能够更加灵活合理地分配利用医疗资源,为数量庞大的老龄人提供基础的医疗服务。在法国荷兰和瑞典等已经发展为比较完善的医疗产业[2-3],在中国也有十分广阔的市场前景。
在家庭医疗护理中,医疗机构可能会依据客户要求提供多次、重复的服务,例如一周2次服务持续半年时间。家庭医疗护理企业为了适应这种多次重复服务的需求,提高人员、车辆等资源的利用率,可以一定长度的时间为周期来考虑资源的调度,将人员、车辆等服务资源安排到周期内的每一天并确定其对客户服务的次序[4]。但是在一个较长的周期中进行资源调度时,一些因素容易出现不确定性的变化,对资源的调度产生困难。
常见的一种不确定因素是客户可能会临时改变接受服务的日期。家庭护理企业与客户协商服务日期时,客户一般会提出几个备选的方案,如以星期为周期时,客户提出(周一,周二)和(周三,周四)两个方案,由企业加以选择并在选定的日期组合内提供服务。为方便陈述,本文将周期内的每个备选服务方案称为一个“服务日期组合”。客户和企业确定了服务日期组合后一般是不改变的。但是在一个较长周期内,显然有部分客户不能完全确定自己的服务日期组合,或者需要改变服务日期组合的情况。例如,客户本周在(周一,周二)获得服务,但是在下周可能只能在(周三,周四)接受服务,其服务日期组合呈现不确定性质。当一定比例的客户都具有不确定的未来服务日期组合时,企业必须针对性制定适应不确定性的资源调度方案,以保证服务质量并尽量减少企业的的运营成本。
对家庭医疗护理资源调度问题的研究很多,其中对医护人员的排班调度问题比较早期的研究有:Jaumard[5]利用列生成方法考虑护士的排班并最小化工作成本,平衡工作时间;Rasmussen等[6]考虑了一系列的边界划分问题并提出了一种分支定价算法求解医护人员的调度问题;Mankowska等[7]考虑了在服务过程中一些客户需要一天多次或者一次多人员护理的情况。此外,在对服务次序的调度研究中,存在用相似模型来解决的方案。如果将每个医护人员看作是移动的服务车辆,则对客户访问次序优化问题就可以近似为某种旅行商问题(traveling sales-man problem,TSP)或车辆路径问题(vehicle routing problem,VRP),而这2种问题已经有了非常广泛的研究。Yannick等[8]和Allaoua等[9]将医护人员的服务路线规划看作带时间窗的多重旅行商问题(multi-ple traveling salesman problem with time windows,MTSPWT)的拓展。Liu和Xie[3]将家庭医疗护理中的物品配送与回收问题转化为带有时间窗的特殊VRP并求解。
本文研究的家庭医疗护理中的资源调度问题与周期性车辆路径问题(periodic vehicle routing pro-blem,PVRP)有一定相似性。PVRP主要包含两个部分:选定客户访问日期的组合,规划出每天的客户访问次序。PVRP最早的启发式算法是由Beltrami等[10]和Russell等[11]提出的;Cordeau等[12]提出了一种禁忌搜索的启发式算法求解PVRP;Hemmelmayr等[13]和Vidal等[14]分别使用变邻域启发式算法和混合遗传算法来求解。
虽然目前对家庭护理资源调度问题存在广泛的研究,但是还没有发现同时考虑周期性和不确定性的研究。相比于PVRP,本文研究中增加客户服务日期组合存在不确定性的情况,即存在一定比例的不确定客户,只有在周期的服务开始时才能确定自己的服务日期组合。由于企业考虑到服务质量问题,必须满足客户的要求,因此在制定即将服务的方案时就必须充分考虑不确定性因素,提供具有鲁棒性的服务方案来指导医护人员的分派和线路的规划。在客户变化服务日期时,服务方案要能柔性调整路线满足客户的需求,并使企业运作成本最小化。
1 问题介绍本文涉及的家庭医疗护理资源调度问题可基于图G=(V,A)表示,其中V=(0, 1,…,n)是n+1个点的集合,0代表医疗中心,其余的点代表n个客户,设每个客户所需的服务时间相同为d,A={(i,j):i,j∈V,i≠j},是路径的集合,定义cij
为客户i和客户j之间医护人员的移动距离成本,成本cij
不随服务日期、服务人员的不同而改变。设服务人员或车辆k∈K的平均移动速度为v。本文考虑服务的周期时长为t天,l∈{1, 2,…,t}为周期内的某一天。
在建立服务关系前,客户要向医疗机构提供自己可接受服务的日期组合方案。定义服务模式Ci ,代表客户i的所有服务日期组合的集合。客户将服务模式反馈给医疗机构后,医疗机构可选择其中任意一个日期组合提供服务。
设定在总数为n的客户中,存在δn 的客户是不确定客户,δ为比例系数,在一个服务周期开始前,他们不能确定此周期哪个日期组合可以接受服务。设定每个不确定客户的日期组合出现概率为pi 。例如客户i的服务模式Ci ={(1), (2), (3)},出现概率pi ={0.8, 0.1, 0.1},则客户i有80%的概率在第1天接受服务,第2、第3天各有10%的概率接受服务,规定在客户服务模式变化时必须按照客户要求的次数和日期提供服务,不允许出现忽略不服务的情况。
同时,依据实际企业调研,本文对研究的问题提出如下约束。
| $\quad\quad \sum\limits_{k \in K} {\sum\limits_{j \in V} {x_{ijk}^l} {\text{≤}} 1,} i \in V\backslash \{ 0\} ,l \in t{{\text{;}}}$ | (1) |
| $\quad\quad \sum\limits_{j \in V} {x_{ijk}^l} - \sum\limits_{i \in V} {x_{jik}^l} = 0,j \in V\backslash \{ 0\} ,l \in t,k \in K{{\text{;}}}$ | (2) |
| $\quad\quad \sum\limits_{j \in V\backslash \{ 0\} } {x_{0jk}^l} = 1,k \in K,l \in t{{\text{;}}}$ | (3) |
| $\quad\quad \sum\limits_{j \in V\backslash \{ 0\} } {x_{j0k}^l} = 1,k \in K,l \in t{{\text{;}}}$ | (4) |
| $\quad\quad x_{ijk}^l = \{ 0,1\} ,i,j \in V,k \in K,l \in t{{\text{。}}}$ | (5) |
约束(1)表示每个客户都每天最多接受一次服务;约束(2)~(4)所有的服务路线必须从医疗中心出发,最终回到医疗中心;约束(5)表示决策变量为0-1变量。
最终问题求解结果是给出成本最小的计划服务方案,方案包含2部分:确定所有客户服务日期的组合,并规划出医护人员对客户的访问次序和路线。方案有三方面的成本:1)医护人员路线移动成本,如公共交通费用或医护车辆的行驶费用。2)每个医护人员出发所需的固定成本C,如前期准备成本。3)医护人员超过标准工作时长D后的加班惩罚成本P,P=α(DA–D),其中,DA为实际工作时长,包括路上行驶时间和为该线路上客户服务的时间;α为惩罚系数。需要注意的是,由于不允许出现客户不被服务的情况,所以本文构造计划服务方案时会将不确定客户的每一种服务日期组合都放入路线规划中。
对于不确定性优化问题,当得到求解结果即计划服务方案后,在执行前通过与客户确定服务日期后再生成实际服务方案。本文采用如下方法生成实际服务方案并计算对应计划服务方案的成本:在被取消的日期内服务资源(如医护人员)直接跳过该客户,按照计划服务方案的访问顺序直接至下一位客户点。具体如图1 所示。
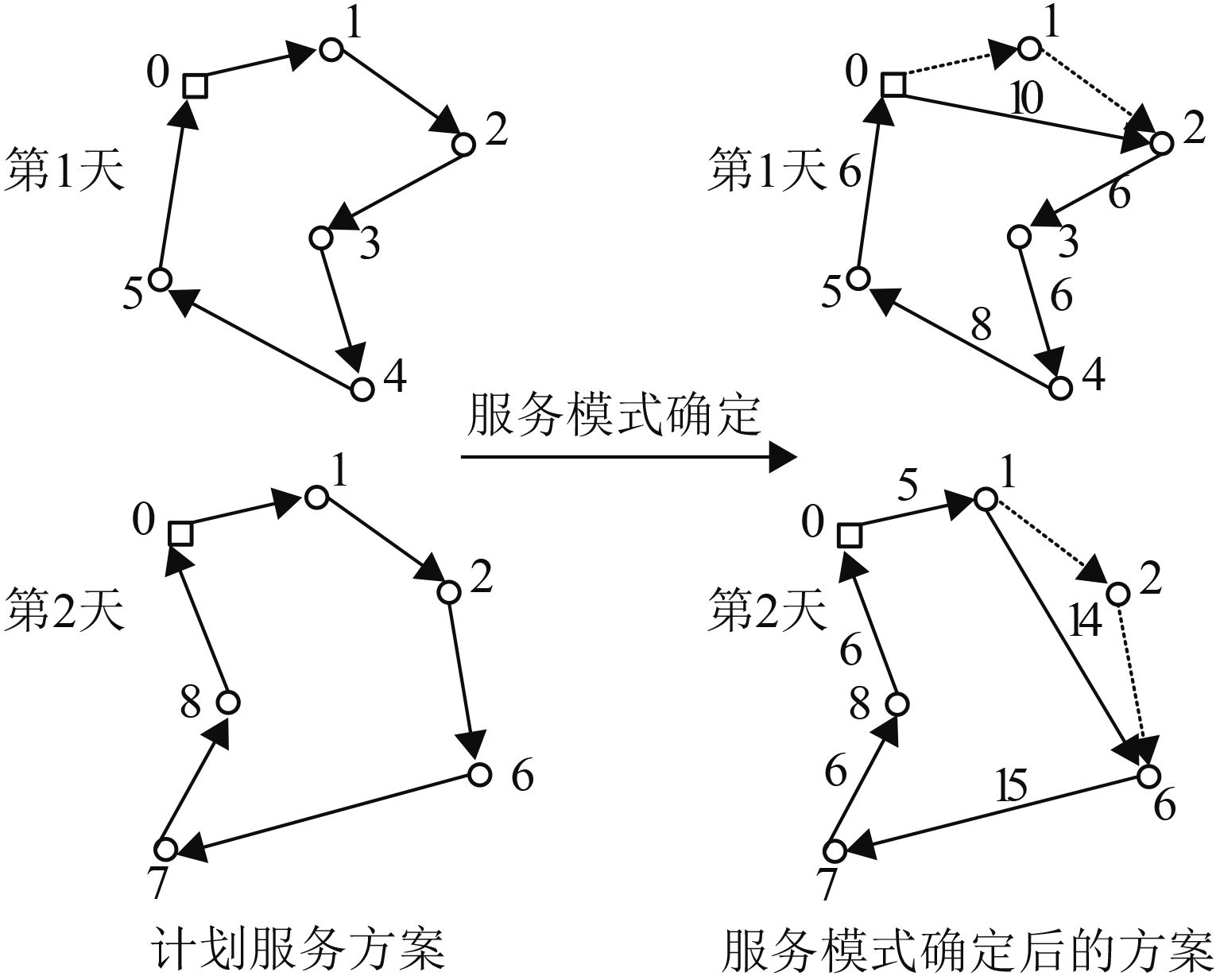
|
图 1 生成实际服务方案 Fig. 1 Generate practical sevice solution |
如图1所示,不确定客户1和2的服务模式C1,C2都是{(1), (2)},即在第1和第2天会随机选择一天接受服务。在生成计划服务方案时,假设1、2号客户在2天都将被服务,得到图1左侧的2条路径。当变化因素确定时,如1、2号客户分别选择了第2天、第1天接受服务,在计划服务方案中直接跳过该客户取消的日期中的位置,便可以得到图1的右侧的路径,即实际的服务方案。
客户间移动成本如图所示,设移动速度v=10,客户服务时间d=1,D=8,α=10,C=30。该服务计划的路线移动成本为36+46=82;固定成本为30+30=60;惩罚成本为0+10×(4.6+4–8)=6;在1、2号客户确定服务模式生成的场景下,该计划服务方案的总成本为148。
2 算法设计 2.1 禁忌搜索算法框架禁忌搜索算法是邻域搜素方式的一个拓展,由一个初始解开始,在划定的空间内朝着使目标函数值最优的方向进行迭代变换,通过一种动态的记忆结构来设定相应的禁忌准则,避免陷入局部最优。本文分别在路径中的单点移动(1-Move)、两点交换(2-Exchange)以及客户服务模式改变构造的3种邻域内搜索问题的最优解,算法整体框架如图2所示。
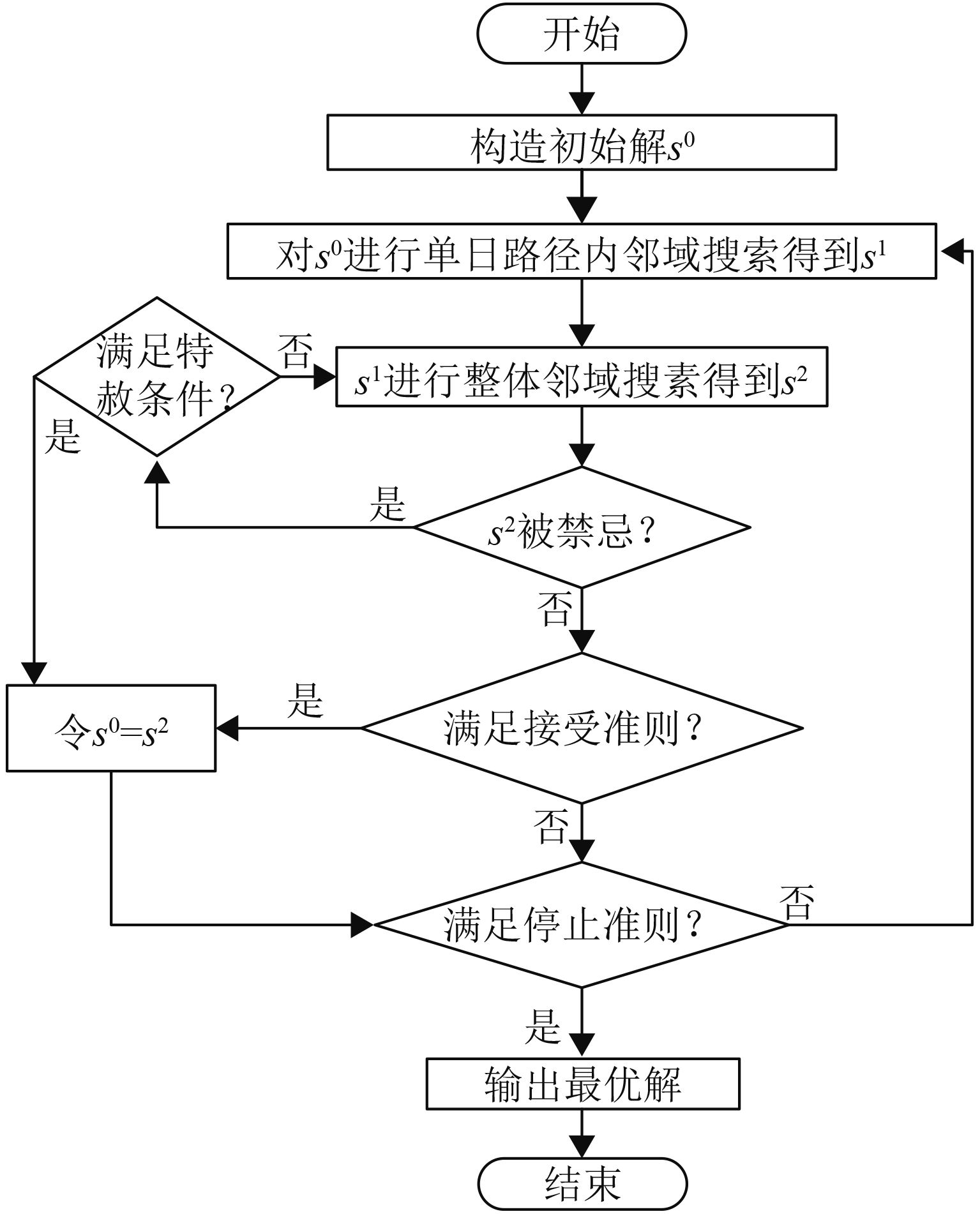
|
图 2 禁忌搜索算法框架 Fig. 2 Framework of tabu search algorithm |
如图2所示,算法首先利用节约算法(saving algo-rithm,CW)生成初始解s0,并且设为算法的当前解s*。然后再进行单日内邻域搜索,寻找最优解s1。然后以s1为初始解进行第2阶段在周期内进行服务模式改变的邻域搜索,得到新的解s2,判断s2是否满足接受准则,如果满足则设定s0=s2,如不满足则进行下一轮迭代。判断是否满足停止准则,如未满足则继续迭代搜索,一直达到算法终止条件。后续章节中将描述算法中的具体方法。
2.2 初始解构造CW算法是一种常见且简单的启发式算法,可在短时间内构造可行解,广泛用于构建初始解[15]。首先从每个普通客户服务模式中随机选取一个服务日期组合,同时选取不确定客户的服务模式中所有的服务日期组合,然后统计出每天需要提供服务的客户,作为确定性问题进行服务线路初始解的构造。
初始解构造具体的步骤如下。
步骤1 构造解s0,每条路线只安排一个客户;
步骤2 计算每两条路线合并后,新路线相对于合并前两条路径成本的减小值,记为节约值;
步骤3 找到第l天不同路径中节约值最大的两条路径进行合并,直到找不到大于零的节约值停止;
步骤4 l∈{1, 2,…,t},以天为单位进行步骤3,直到得到周期内每天的线路;
步骤5 初始解构造结束,输出初始解s0。
2.3 成本评价方式 2.3.1 蒙特卡洛仿真邻域搜索的过程中需要多次评价线路成本,由于存在不确定因素,用解析的方式来评价难度很大,而通过蒙特卡洛仿真方法模拟现实中发生的情况来评价成本则相对简单[16]。
本文利用蒙特卡洛仿真,模拟不确定客户随机挑选服务模式的过程,实例化每一个不确定客户的服务情况,生成一个场景,随后便可以得到一个实际服务方案进行成本评价。
定义蒙特卡洛仿真次数为M,即进行M次场景生成从而对现实进行模拟,具体步骤如下。
步骤1 依据出现概率pi 为每一个不确定客户选择一个服务模式;
步骤2 依据选出的服务模式日期,删除计划服务方案中的不能接受服务的不确定客户点;
步骤3 按照图1中方式计算线路成本。判断是否结束仿真,没结束则并回到步骤1,结束则到步骤4;
步骤4 将M次模拟的线路成本的期望,得到该计划服务方案在现实中的成本。
2.3.2 蒙特卡洛仿真中解评价的快速评价方法在蒙特卡洛仿真对解进行成本评价的过程中,为了保证评估准确,仿真次数M必须足够多(一般为1 000或更多次),使得运算时间变长。为了缩短算法的时间,在特定情况下,本文提出了一种快速的评估方式:初始解生成后,通过仿真计算其成本包括:线路移动成本、固定成本以及加班惩罚成本,同时经过M次仿真后也可以得到每位医护人员的平均工作时间。当移动的某一客户本身是确定客户而且其左右位置的客户点也是确定客户时(医疗中心0也视为确定客户),变化后的线路成本可以在之前成本的基础上加上其移动后对成本改变的变化值得到,不需要仿真。具体的操作如图3所示。
客户1、2、3是不确定客户,客户4、5为确定客户。当客户5被移出该路线时,其自身以及相邻的左右点均为确定客户。分析新线路成本的变化:1)线路移动成本,客户1、2、3的仿真过程中的选择不变,M次仿真中,与移出前相比路线成本的变化都是∆=c40-c45-c50,因此,新的路线成本即为原路线成本加上∆;2)固定成本,医护人员不变,所以固定成本不变;3)惩罚成本,在初始路线医护人员的平均工作时间上减去移出客户5所带来的时间变化(包括客户5的服务时间d和减少的距离的移动时间),即为新路线的医护人员工作时间,依据新的工作时间计算出惩罚成本。
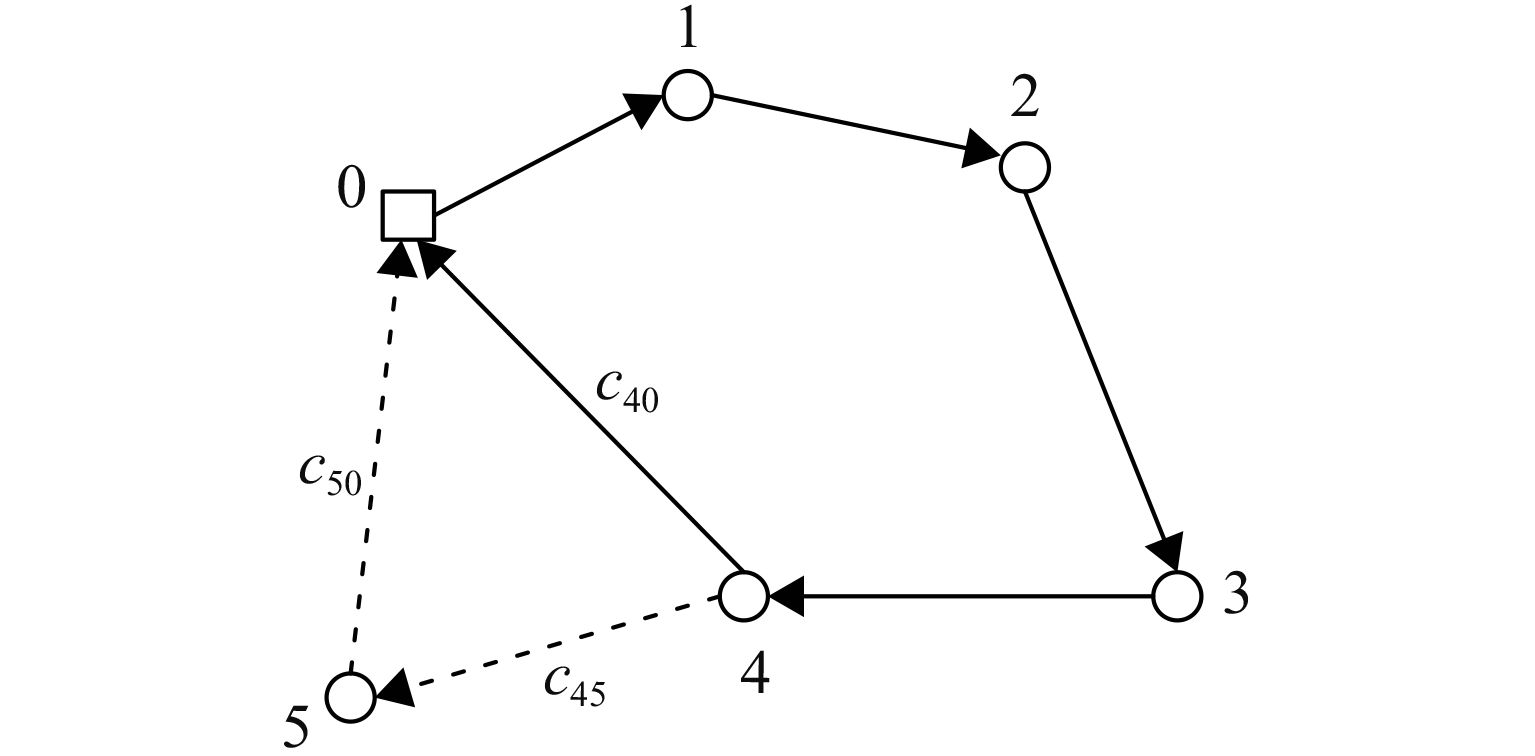
|
图 3 快速评估方法 Fig. 3 A way to quickly estimate the cost |
这种快速评价的方法,减少了使用仿真的频率,可以节约大量的运算时间。
2.4 求解空间与邻域搜索本文设计的禁忌搜索算法设计了3种邻域:对单日线路进行单点客户的位置改变而获得解s1邻域集合N(s1);对单日路径内两客户点进行交换而获得新的解s2邻域集合N(s2);还有对客户的服务模式改变而产生的新的解的邻域集合N(s2)。
2.4.1 单日内线路搜索单日内的线路内可以构造两种邻域,单个客户位置移动,两客户进行位置交换。单点移动的基本思路是依次尝试将不同客户移动到当天的路径中的每一个位置,计算改变位置后的成本。如图4中将客户i移动到j处。
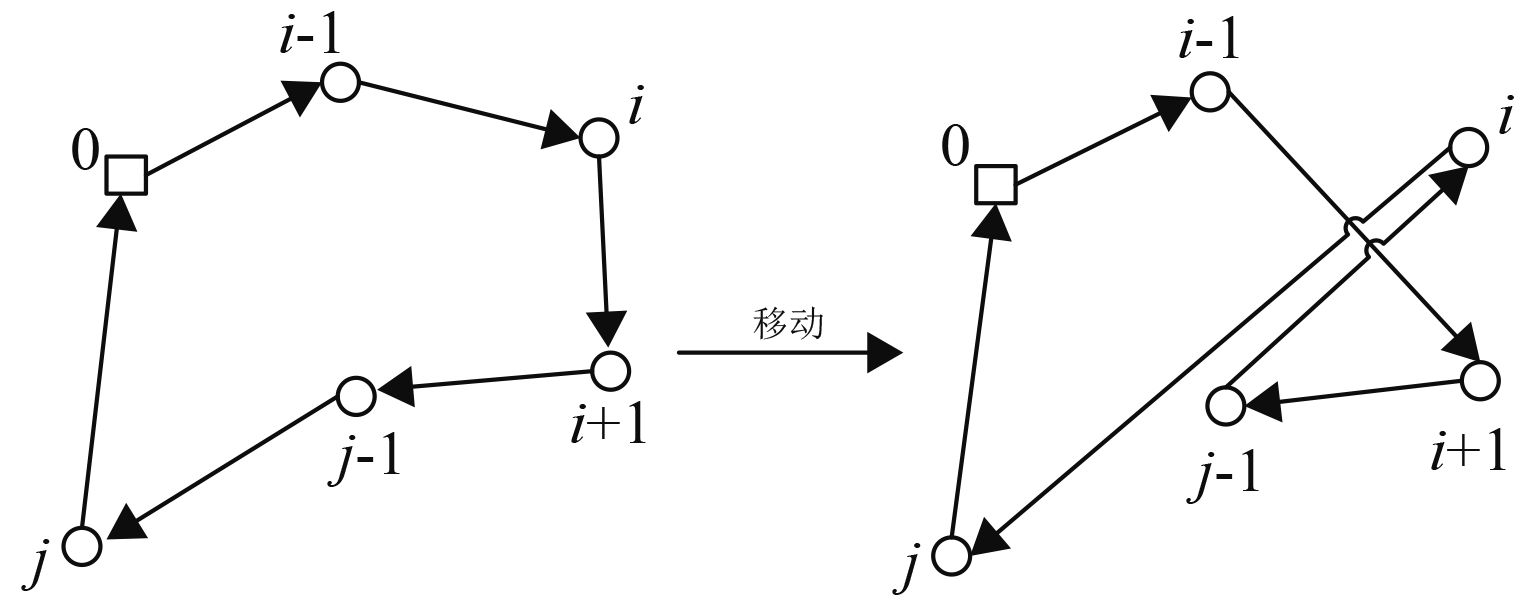
|
图 4 单点移动 Fig. 4 1-Move |
两点交换即依次交换线路中两点的位置。如图5所示,i和j点交换,其中虚线为交换前i所在的线路,实线为交换前j所在的线路。
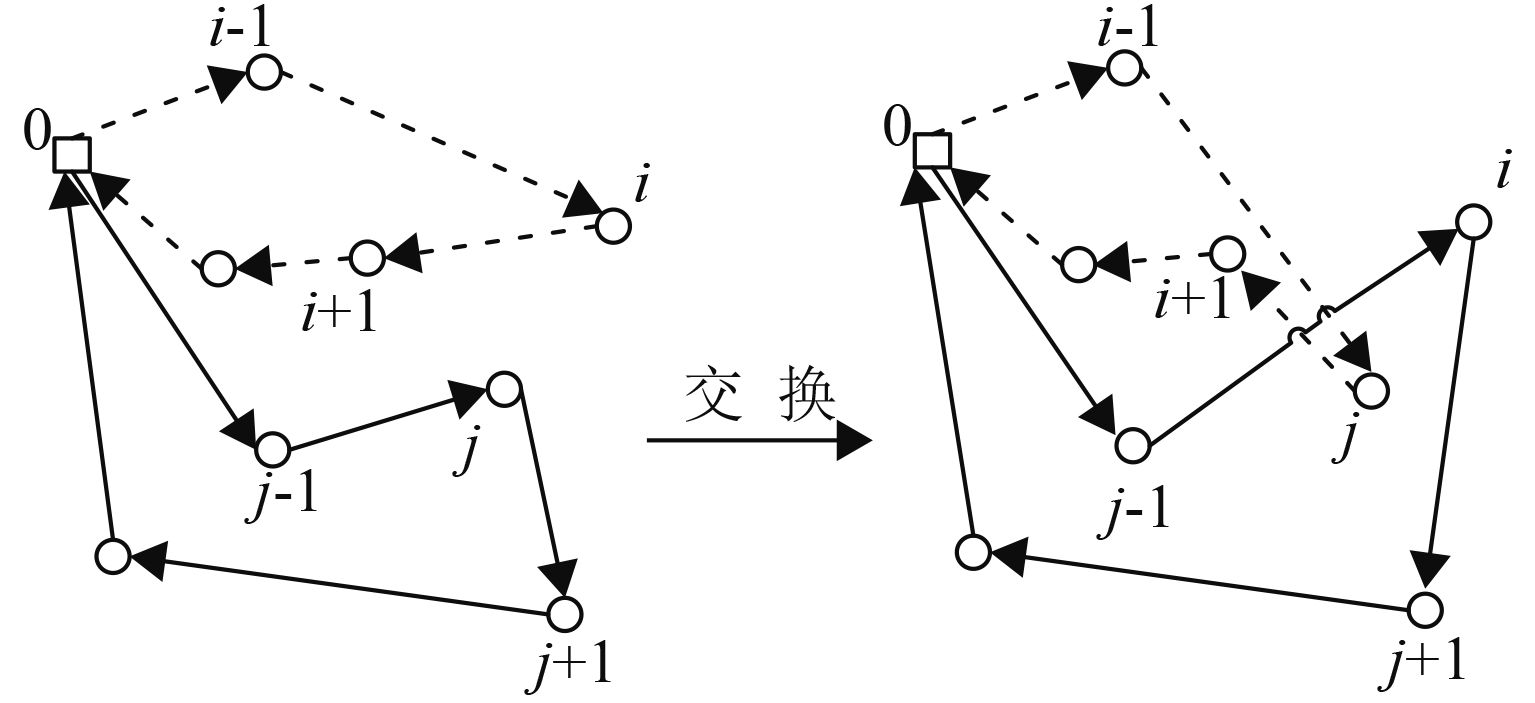
|
图 5 两点交换 Fig. 5 2-Exchange |
单日内的线路搜索遵循的是选取首优原则(first accepted,FA),在每一轮的搜索过程中,只要变化后产生新的解s1的成本f(s1)比初始解的s0的成本f(s0)更优就立即选取s1作为新的解,然后回到起始再次开始搜索,直到找不到更优解为止。
2.4.2 周期内邻域搜索由于不确定客户的服务日期都包含在服务方案中,所以是由确定性客户的服务模式改变而生成的邻域。依次改变每一个确定客户的服务模式,评价此时的整个周期的路线成本。对所有客户服务模式进行一轮搜索之后,找到整体成本最优所对应的一组服务模式下的服务方案s2,与当前最优解s*对比,如果f(s2)比当前最优解的成本f(s*)更优则替换为当前解,继续迭代,直到达到停止标准。
2.5 禁忌准则、特赦准则多样化方法和停止准则禁忌准则:当客户i从将服务模式从Ci (a)改变为Ci (b)后,得到当前迭代的最优解时,客户i的服务模式在后续的θ次连续迭代中都不能再次回到Ci (a)。本文采用的特赦准则为若某一被禁忌的服务模式能得到比已知最优解更优的解,则该次改变被特赦。
为了增加搜索的多样性,本文引入了一种模拟退火算法的接受准则。当邻域搜索得到的新的解s2的成本f(s2)大于旧的解s1的成本f(s1)时,仍然以一定的概率来接受s2,并迭代到下一轮搜索中。接受概率为
| $\quad\quad {{\rm{e}}^{ - \left[ {(f({s^2}) - f({s^1}))} \right]/T}}{{\text{。}}}$ | (6) |
其中,T>0为退火温度。每一次迭代后T=T×c,其中0<c<1,是冷却比。T会随着迭代次数的增加而逐渐变小,算法接受差解的概率也会越来越小。通过接受非最优解,避开局部最优,搜索更多区间。
停止准则:对所有客户服务模式进行一轮搜索后,即算为迭代一次。设定当迭代到达2 000次,或者当连续500代搜索没有更优解出现时停止迭代。
3 实验分析由于不确定性周期性家庭医疗护理资源调度问题较为新颖,没有标准的测试算例,本文借用了Cordeau[12]的PVRP的部分算例,随机生成了各个客户的服务模式。创造了20、50、100、200四种客户规模的的算例,同时设定了δ=20%和δ=40%两种不确定客户的比例。
为了验证所提出的算法的可行性,本文构造了一种对比算法:在生成计划服务方案时,同样需要将所有的不确定客户的服务模式考虑进去;但是在禁忌搜索过程中评价线路成本时,并不使用蒙特卡洛仿真方法来模拟现实中出现的情况,不对多余的不确定客户进行删除,而是直接计算每条路线的成本的大小。通过相同的邻域的禁忌搜索方式,得到了计划服务方案后,再使用蒙特卡洛仿真模拟现实中的场景,对最终的计划服务方案进行评价。
为了保证对比实验的有效性,将2种方法的运行时间控制在同一水平,重点比较成本的大小。其中对于规模100和200的算例,将其迭代时间分别限定为1 h和2 h。本文所有程序均通过C++实现,运行于Intel Xeon E5-2670 2.6 GHz CPU,2 GB内存计算机。
| 表 1 算法参数取值 Tab. 1 Value of varibles |
从表2和表3中可以看出,在20、50小规模算例中都有90%的解优于对比方法,平均成本的降低幅度为7%和8%;在100、200大规模的算例中,70%和80%的解优于对比方法。成本平均的降低幅度为14%和0.2%。随着20到100算例规模的增大,相比于对比算法,平均成本降低的幅度也增大。在200规模的算例中,虽然有80%以上的算例得到比对比算法更优的解,但是成本降低的幅度非常小。经过分析,原因可能是200规模的算例较大,限定的迭代时间有限,因此不能充分迭代找到更优的解。
| 表 2 δ=20%小规模算例算例测试结果 Tab. 2 Result of small scale instance withδ=20% |
| 表 3 δ=20%大规模算例测试结果 Tab. 3 Result of large scale instance withδ=20% |
从表4和表5可以看出,在δ=40%的情况下,各算例的结果相对于δ=20%都有所增大。20、50、100、200规模的算例中,分别有85%、80%、70%、70%的解优于对比方法。成本平均的降低幅度分别为7%、9%、13%、0%。在100、200大规模的算例中,虽然有70%以上的算例得到比对比算法更优的解,但都是成本降低的幅度都小于δ=20%时的算例,经过分析,δ=40%时,不确定因素增多,计算量相应增大,迭代时间也加长,由于时间限制,迭代不如δ=20%时充分,导致提升效果下降。
| 表 4 δ=40%小规模算例算例测试结果 Tab. 4 Result of small scale instance withδ=40% |
| 表 5 δ=40%大规模算例算例测试结果 Tab. 5 Result of large scale instance withδ=40% |
针对不确定性的周期性家庭医疗护理资源调度问题,本文建立了相应的模型,提出了一种禁忌搜索算法对其求解,并得到了有效的结果。本文提出的算法比对比算法在得到成本更加优秀的解。在本文的研究基础上,后续可以从考虑100、200大规模问题通过特定分解后再求解,以减少算法时间。
| [1] | LANZARONE E, MATTA A, SAHIN E. Operations management applied to home care services: the problem of assigning human resources to patients[J]. Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on, 2012, 42(6): 1346-1363. DOI: 10.1109/TSMCA.2012.2210207. |
| [2] | EVEBORN P, FLISBERG P, RONNQVIST M. Laps Care—an operational system for staff planning of home care[J]. European Journal of Operational Research, 2006, 171(3): 962-976. DOI: 10.1016/j.ejor.2005.01.011. |
| [3] | LIU R, XIE X, AUGUSTO V. Heuristic algorithms for a vehicle routing problem with simultaneous delivery and pickup and time windows in home health care[J]. European Journal of Operational Research, 2013, 230(3): 475-486. DOI: 10.1016/j.ejor.2013.04.044. |
| [4] | STEEG J, SCHRODER M. A hybrid approach to solve the periodic home health care problem[M]//Operations Research Proceedings 2007. Springer Berlin Heidelberg, 2008: 297-302. |
| [5] | JAUMARD B, SEMET F, VOVOR T. A generalized linear programming model for nurse scheduling[J]. European journal of operational research, 1998, 107(1): 1-18. DOI: 10.1016/S0377-2217(97)00330-5. |
| [6] | RASMUSSEN M S, JUSTESEN T, DOHN A. The home care crew scheduling problem: Preference-based visit clustering and temporal dependencies[J]. European Journal of Operational Research, 2012, 219(3): 598-610. DOI: 10.1016/j.ejor.2011.10.048. |
| [7] | MANKOWSKA D S, MEISEL F, BIERWIRTH C. The home health care routing and scheduling problem with interdependent services[J]. Health care management science, 2014, 17(1): 15-30. DOI: 10.1007/s10729-013-9243-1. |
| [8] | KERGOSIEN Y, LENTE C, BILLAUT J C. Home health care problem: An extended multiple traveling salesman problem[C]//Proceedings of the 4th Multidisciplinary International Conference on Scheduling: Theory and Applications Dublin MISTA, 2009: 85-92. |
| [9] | BORNE H A S, LETOCART L, CALVO R W. A matheuristic approach for solving a home health care problem[C]// International Network Optimization Conference. 2013. |
| [10] | BELTRAMI E J, BODIN L D. Networks and vehicle routing for municipal waste collection[J]. Networks, 1974, 4(1): 65-94. DOI: 10.1002/(ISSN)1097-0037. |
| [11] | RUSSLL R, IGO W. An assignment routing problem[J]. Networks, 1979, 9(1): 1-17. DOI: 10.1002/(ISSN)1097-0037. |
| [12] | CORDEAU J F, GENDREAU M, LAPORTE G. A tabu search heuristic for periodic and multi-depot vehicle routing problems[J]. Networks, 1997, 30(2): 105-119. DOI: 10.1002/(ISSN)1097-0037. |
| [13] | HEMMELMAYR V C, DOERNER K F, HARTL R F. A variable neighborhood search heuristic for periodic routing problems[J]. European Journal of Operational Research, 2009, 195(3): 791-802. DOI: 10.1016/j.ejor.2007.08.048. |
| [14] | VIDAL T, CRAINIC T G, GENDREAU M. A hybrid genetic algorithm for multidepot and periodic vehicle routing problems[J]. Operations Research, 2012, 60(3): 611-624. DOI: 10.1287/opre.1120.1048. |
| [15] | GOLDEN B, ASSAD A, LEVY L. The fleet size and mix vehicle routing problem[J]. Computers & Operations Research, 1984, 11(1): 49-66. |
| [16] | BIRATTARI M, BALAPRAKASH P, STUTZLE T. Estimation-based local search for stochastic combinatorial optimization using delta evaluations: a case study on the probabilistic traveling salesman problem[J]. INFORMS Journal on Computing, 2008, 20(4): 644-658. DOI: 10.1287/ijoc.1080.0276. |
 2017, Vol. 20
2017, Vol. 20