碳足迹(carbon footprint)是以CO₂为标准衡量全部温室气体排放。本文中碳足迹定义既指产品或服务，也包括某一活动过程在其生命周期排放的CO₂总量^[1]。考察传统供应链的碳足迹以后，原有决策分析必然发生变化。生产与库存是供应链的重要组成部分，通过运作策略有效减少这些环节的碳足迹是一个重要的学术课题，无论对于企业的节能降耗，还是对于低碳社会都具有重要意义。

供应链碳足迹已引起国内外学者的关注，如在三维空间上计算四级供应链碳足迹^[2]，库存系统的碳足迹^[3]，供应链运输活动的碳足迹和能源消耗^[4]，双源进货渠道的碳足迹^[5]，不同类型的碳足迹对供应链运营的影响^[6]等。以上文献多采用描述模型，用案例描述碳足迹计算过程与方法，而针对供应链生产-库存环节碳足迹建模度量的研究，还很少涉及。

与本文有关的另一部分文献是多级生产-库存问题，带有二级市场的多级库存系统协调^[7]，多阶段供应链的经济批量和配送调度的同步策略^[8]，四级供应链网络的优化^[9]，五级制造供应链的订货与生产协调^[10]。这些多级文献无论是研究方法，还是系统复杂性上都有很大的进步，却不涉及供应链碳减排问题。

本文基于多供应商、单制造商和多零售商构成的三级复杂网络，通过碳足迹质量平衡方程准确度量供应链运输、库存与生产过程碳排放数量，考察碳足迹对供应链运营的影响。系统中零售商r需求是产品价格的分段函数D_r =f(p)，制造商生产k种产品，需要i种原料，每个供应商供应一种或多种原料；当制造商收到第r个零售商订货量Q_rk 时，制造商生产λ_mrkQ_rk (λ_mrk ≥1)以应对零售商r的需求波动，同时向s个供应商订购原材料u_iλ_mrkQ_rk ，供应商收到订单后，备货λ_srkλ_mrku_iQ_rk (λ_srk ≥1)向制造商配送。政府部门按照“基准制”原则统一分配碳配额给供应链成员，存在碳交易市场为成员提供碳配额现货交易，交易行为直接影响其收益。由此得出多级生产-库存-碳足迹模型，使用改进EOQ处理不确定需求，进一步研究碳配额分配政策、市场交易变动供应链生产、订货及碳足迹之间的关系。本文的贡献如下：1)基于过程建立碳足迹质量平衡方程，准确核算供应链碳足迹；2)通过多级生产–库存–碳足迹模型，研究多级成员运营与环境的协调，并用协调效率曲线分析供应链协作价值；3)分析碳配额分配政策与微观市场作用下供应链运营效果，选择适宜的排放控制手段。

1 符号说明 1.1 决策变量

Q_rk 为零售商r订购商品k的数量；

T为三级系统集中决策的订货周期；

λ_mrk 为制造商对于订货量Q_rk 的生产倍数；

λ_srk 为供应商对于制造商订货的备货倍数。

1.2 参数符号

s为供应商的数量，s=1, 2,…,g；

i为原材料种类，i=1, 2,…,w；

O_s 为供应商s的订货成本，与原料类型无关；

h_si 为供应商s持有原料i的单位成本；

w_s 为供应商s提供的原料种类数， $w = \sum\limits_{s = 1}^g {{w_s}} $ ；

k为产品种类，k=1, 2,…,j；

S_m 为制造商每次生产固定启动成本；

h_mk 为制造商持有单位产成品k的成本；

O_i 为制造商订购第i种原料订货成本；

u_i 为制造商每单位产成品需要i种原料数量；

h_mi 为制造商持有单位原料i的成本；

q_mk 为制造商生产单位k产品的加工成本；

r为零售商数量，r=1, 2,…,n；

D_rk 为零售商r对产品k的需求率；

T_rk 为零售商r订购商品k的周期时间；

O_rk 为零售商r每次订购k产品的订货成本；

h_rk 为零售商r持有k商品的单位成本；

p_k 为产品k的需求价格；

C_s 为分配给供应商s的碳配额；

C_m 为分配给制造商的碳配额；

C_r 为分配给零售商r的碳配额；

P为碳交易价格；

TR_z为可交易碳额度，z=s,m,r(正值表示卖出，负值表示买入)；

E_sf为供应商s每次订货固定碳足迹；

E_sih为供应商s持有原料i的单位库存碳足迹；

E_mif为制造商每次订购原料i的固定碳足迹；

E_mkh为制造商持有产成品k的单位碳足迹；

E_mih为制造商持有原料i的单位碳足迹；

E_mkp为制造商生产单位产品k的碳足迹；

E_rkf为零售商r每次订购商品k的固定碳足迹；

E_rkh为零售商r持有k商品单位碳足迹。

2 供应链碳足迹分析 2.1 碳足迹过程刻画

按照PAS2050提出的碳足迹计量方法，界定本文碳足迹包括3个阶段。第1阶段，供应商碳足迹。即向外部供应商订货起至下游制造商发出订单前这一时期的碳足迹，包括运输与储存活动，产生的排放计入运输碳足迹与库存碳足迹。第2阶段，制造商碳足迹。从上游供应商运输订货起至下游零售商发出订单前产生的二氧化碳，包括运输、加工转化、储存3个过程，分别计入运输碳足迹、生产碳足迹、库存碳足迹。第3阶段，零售商碳足迹。从零售商向上游制造商发出订单起到零售商将产品交付至下游顾客期间的碳足迹，主要是运输与储存活动产生的运输碳足迹与库存碳足迹。

2.2 碳足迹质量平衡方程

质量平衡方程是根据系统输入与输出关系，使供应链碳足迹达到平衡状态，得出基本的三级碳足迹质量平衡等式

$\begin{split}& \quad \quad {\rm{TR}} = \sum (T{R_r} + {\rm{T}}{{\rm{R}}_m} + {\rm{T}}{{\rm{R}}_s}) =\\ & (\sum\limits_{s = 1}^g {{C_s}} + {C_m} + \sum\limits_{r = 1}^n {{C_r}} ) - ({E_{\rm{T}}} + {E_{\rm{W}}} + {E_{\rm{P}}}){{\text{。}}}\end{split}$

(1)

其中，E_T表示运输碳足迹；E_W表示库存碳足迹；E_P表示生产碳足迹。式(1)表示供应链可交易碳额度等于各成员可交易碳额度之和，或总分配额与3种碳足迹之差。

2.2.1 运输碳足迹

运输碳足迹(E_T)主要是订货运输过程产生，本文零售商需求是产品价格的函数，按照Whitin^[11]的研究，仍然适用于经典EOQ模型。假设各节点成员订货采用不同载重车辆整车运输，车辆运输能力无限，运输碳足迹与订货次数相关。这样，当零售商r发出订单Q_rk 时，制造商按λ_mrk 倍投入生产，供应商按制造商订货供给λ_srk 倍原材料，得出三级供应链运输碳足迹方程

$\begin{split}& \quad\quad {E_{\rm{T}}} = \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{{E_{rk{\rm{f}}}}{D_{rk}}}}{{{Q_{rk}}}}} } + \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\sum\limits_{i = 1}^w {\frac{{{E_{mi{\rm{f}}}}{D_{rk}}}}{{{\lambda _{mrk}}{Q_{rk}}}}} } } +\\ & \sum\limits_{s = 1}^g {\sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{{E_{s{\rm{f}}}}{D_{rk}}}}{{{\lambda _{srk}}{\lambda _{mrk}}{Q_{rk}}}}} } } \text{。}\end{split}$

(2)

式(2)中依次是零售商、制造商、供应商的运输碳足迹。

2.2.2 库存碳足迹

由于使用EOQ方法处理不确定需求的近似结果与实际值偏差不大^[12]。所以零售商平均库存水平的近似值为Q_rk /2，制造商每种原材料库存为u_i (λ_mrk -1)Q_rk /2，各产成品的平均库存为(λ_mrk -1)Q_rk /2，供应商第i种原材料库存水平是u_iλ_mrk (λ_srk -1)Q_rk /2，假设节点成员库存碳足迹与存货数量均为线性相关，则系统库存碳足迹方程为

$\begin{split}& \quad\quad {E_{\rm{W}}}\!=\!\!\! \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{{E_{rk{\rm{h}}}}{Q_{rk}}}}{2}} } \!+\!\!\! \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{{E_{mk{\rm{h}}}}}}{2}} ({\lambda _{mrk}} \!-\! 1){Q_{rk}}} + \\& \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{\sum\limits_{i = 1}^w {{E_{mi{\rm{h}}}}{u_i}} }}{2}({\lambda _{mrk}} - 1){Q_{rk}}} } + \\& {\sum\limits_{s = 1}^g {\sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{\sum\limits_{i = 1}^w {{E_{sih}}{u_i}_m} }}{2}({\lambda _{srk}} - 1){Q_{rk}}} } } }{{\text{。}}}\end{split}$

(3)

式(3)由零售商库存、制造商产成品库存、制造商原材料库存、供应商库存碳足迹构成。

2.2.3 生产碳足迹

生产碳足迹是制造商加工转化过程发生，不考虑制造商固定设备排放，全部排放与生产数量线性相关，生产碳足迹为

$\quad\quad {E_{\rm{P}}} = \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {{\lambda _{mrk}}{Q_{rk}}} } {E_{mk{\rm{p}}}}{{\text{。}}}$

(4)

即生产碳足迹是加工转化数量与单位生产碳排放的乘积。

3 三级生产-库存-碳足迹模型 3.1 零售商库存-碳足迹模型

零售商r在周期内向制造商订货数量为Q_rk ，假设持有成本与库存水平线性相关，根据碳足迹质量平衡方程，零售商r的库存-碳足迹模型为

$\begin{split}& {\rm{TC}}{{\rm{R}}_r} = \frac{{\displaystyle\sum\limits_{k = 1}^j {({O_{rk}} + } P{E_{rk{\rm{f}}}}){D_{rk}}}}{{{Q_{rk}}}} + \frac{{\displaystyle\sum\limits_{k = 1}^j {({h_{rk}} + P{E_{rk{\rm{h}}}}){Q_{rk}}} }}{2} - P{C_r}{{\text{。}}}\end{split}$

(5)

其中，第1项为订货成本与运输碳足迹成本，第2项是库存持有与库存碳足迹成本，第3项是碳交易成本。将零售商r的成本加总即得零售商阶段全部库存-碳足迹成本为TCB。

3.2 制造商生产-库存-碳足迹模型

制造商接到零售商订单Q_rk 时，其实际投产数量为λ_mrkQ_rk ，同时确定所需原材料数量，按类型分批购进，考察每个过程的碳足迹，得出不同零售商订货时制造商生产-库存-碳足迹模型为

$\begin{split}& \quad\quad {\rm{TC}}{{\rm{M}}_r} = \sum\limits_{k = 1}^j {\frac{{({S_m} + \sum\limits_{i = 1}^w {{O_i}} + P{E_{mi{\rm{f}}}}){D_{rk}}}}{{{\lambda _{mrk}}{Q_{rk}}}}} + \\& \sum\limits_{k = 1}^j {\frac{{{h_{mk}} + P{E_{mk{\rm{h}}}}}}{2}({\lambda _{mrk}} - 1){Q_{rk}}} + \\& \sum\limits_{k = 1}^j {\frac{{\sum\limits_{i = 1}^w {({h_{mi}} + P{E_{mi{\rm{h}}}}){u_i}} }}{2}({\lambda _{mrk}}} - 1){Q_{rk}} + \\& \sum\limits_{k = 1}^j {{\lambda _{mrk}}({q_{mk}} + P{E_{mk{\rm{p}}}}){Q_{rk}}} - P{C_m}{{\text{。}}}\end{split}$

(6)

式中第1项是生产启动成本、原材料订购成本与运输碳足迹成本之和；第2项为产成品库存持有与库存碳足迹成本；第3项原材料库存持有与库存碳足迹成本；第4项是生产碳足迹成本，最后一项是碳交易成本。如果全部零售商订货，得出制造商总成本TCM。

3.3 供应商库存-碳足迹模型

供应商收到制造商订单以后，每种原料的备货数量为λ_srkλ_mrku_iQ_rk ，供应商的碳足迹主要产生于运输与存储过程，则供应商s的库存-碳足迹模型为

$\begin{split}& \quad\quad {\rm{TC}}{{\rm{S}}_s} \!=\!\!\!\! \displaystyle\sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{\sum\limits_{i = 1}^w {({h_{si}} \!\!+\!\! P{E_{si{\rm{h}}}}){u_i}{\lambda _{mrk}}} }}{2}({\lambda _{srk}} \!-\! 1){Q_{rk}}} } + \\& \displaystyle\sum\limits_{r = 1}^n {\frac{{\sum\limits_{k = 1}^j {({O_s} + P{E_{s{\rm{f}}}}} ){D_{rk}}}}{{{\lambda _{srk}}{\lambda _{mrk}}{Q_{rk}}}}} - P{C_s}{{\text{。}}}\end{split}$

(7)

式中各项依次为库存持有与库存碳足迹成本、订货与运输碳足迹成本、碳交易成本，供应商阶段全部运营与碳足迹成本为TCS。

3.4 供应链生产-库存-碳足迹模型

将TCB、TCM、TCS加和，即为非协调决策下三级系统生产-库存-碳足迹总成本

$\quad\quad {\rm{TC}} = {\rm{TCB}} + {\rm{TCM}} + {\rm{TCS}}{{\text{。}}}$

(8)

各零售商需求不定，制造商随时处理到达订单，为得出供应链协调结果，假设所有零售商要在制造商确定的统一订货周期内发出订单，由此全部零售商的订货周期T=Q/D，将式(8)转化为关于共同周期T的函数，此时供应链生产-库存-碳足迹模型转化为关于共同订货周期T的函数

$\begin{split}& \quad\quad {\rm{T}}{{\rm{C}}_1}(T) = \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{({O_{rk}} + P{E_{rk{\rm{f}}}})}}{T}} + } \\& \sum\limits_{r = 1}^n {\frac{{\sum\limits_{k = 1}^j {({h_{rk}} + P{E_{rk{\rm{h}}}})T{D_{rk}}} }}{2}} + \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{({S_m} + \sum\limits_{i = 1}^w {{O_i}} + P{E_{mi{\rm{f}}}})}}{{{\lambda _{mrk}}T}}} } +\\& \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{{h_{mk}} + P{E_{mk{\rm{h}}}}}}{2}({\lambda _{mrk}} - 1)T{D_{rk}}} } + \\& \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{\sum\limits_{i = 1}^w {({h_{mi}} + P{E_{mi{\rm{h}}}}){u_i}} }}{2}({\lambda _{mrk}}} - 1)T{D_{rk}}} + \\& \sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {{\lambda _{mrk}}({q_{mk}} + P{E_{mk{\rm{p}}}})T{D_{rk}}} } +\sum\limits_{s = 1}^g {\sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{({O_s} + P{E_{s{\rm{f}}}})}}{{{\lambda _{srk}}{\lambda _{mrk}}T}}} } } + \\& \sum\limits_{s = 1}^g {\sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{\sum\limits_{i = 1}^w {({h_{si}} + P{E_{si{\rm{h}}}}){u_i}{\lambda _{mrk}}} }}{2}({\lambda _{srk}} - 1)T{D_{rk}}} } } - \\& P(\sum\limits_{r = 1}^n {{C_r}} + {C_m} + \sum\limits_{s = 1}^m {{C_s}} ){{\text{。}}}\end{split}$

(9)

由于 $\displaystyle\frac{{{\partial ^2}T{C_1}(T)}}{{\partial {T^2}}} = 2 \displaystyle\sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{({O_{rk}} + P{E_{rk{\rm{f}}}})}}{{{T^3}}}} } + $ $ \quad\quad 2\displaystyle\sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{({S_m} + \sum\limits_{i = 1}^w {{O_i}} + P{E_{mi{\rm{f}}}})}}{{{\lambda _{mrk}}{T^3}}}} } + $ $ \quad\quad 2\displaystyle\sum\limits_{s = 1}^g {\sum\limits_{r = 1}^n {\sum\limits_{k = 1}^j {\frac{{({O_s} + P{E_{s{\rm{f}}}})}}{{{\lambda _{srk}}{\lambda _{mrk}}{T^3}}}} } } {\text{＞}} 0 $ ，

可知TC₁(T)是连续的凸函数，令∂TC₁(T)/∂T=0，得到关于(λ_mrk ,λ_srk )的零售商共同订货周期为

$\quad\quad {T^*}\left( {{\lambda _{mrk}},{\lambda _{srk}}} \right) = \frac{1}{{\sqrt {{D_{rk}}} }}\sqrt {\frac{{\hat A + \hat B + \hat C}}{{\hat D + \hat E + \hat F + \hat G + \hat H}}}{{\text{。}}}$

(10)

其中，

4 模型求解 4.1 非协调模型数学分析解

三级非协调生产-库存-碳足迹模型(8)求解是从确定零售商最优订货数量开始，逐级顺序优化。由于零售商需求是价格的分段函数，即

$\quad \quad {D_{rk}} = \left\{ {\begin{array}{*{20}{l}}{{a_k}{p_k}^2 - {b_k}{p_k} + {c_k},0 {\text{≤}} {p_k} {\text{≤}} b_k/(2a_k);}\\[8pt]{0,{p_k}{\text{＞}} b_k/(2a_k)}{\text{。}}\end{array}} \right.$

其中， ${a_k},{b_k},{c_k} \in + {\rm R} $ ，且 ${b_k}^2 - 4{a_k}{c_k}{\text{＜}} 0$ ， $ {b_k}/(2{a_k})$ 是产品价格的临界点，具体求解步骤如下。

第1步：确定零售商r的最优订货数量(Q_rk )^*。通过式(5)得出

${({Q_{rk}})^*} \!=\! \sqrt {2\sum\limits_{k = 1}^j {({O_{rk}}} + P{E_{rk{\rm{f}}}}){D_{rk}}/\sum\limits_{k = 1}^j {({h_{rk}} + P{E_{rk{\rm{h}}}})} } {{\text{。}}}$

(11)

由于需求是价格的分段函数，将D_rk 的分段函数代入式(11)得出零售商的最优订货量关于价格p_k 的表达式^[12]，

$Q_{rk}^*({p_k}) =\! \left\{ {\begin{array}{*{20}{l}}\begin{array}{l} \sqrt {\!\! \displaystyle\frac{{2\sum\limits_{k = 1}^j {({O_{rk}}} + P{E_{rk{\rm{f}}}})({a_k}{p_k}^2 - {b_k}{p_k} + {c_k})}}{{\sum\limits_{k = 1}^j {({h_{rk}} + P{E_{rk{\rm{h}}}})} }}} ,\\[28pt] 0 {\text{≤}} {p_k} {\text{≤}} {b_k}/(2{a_k}){\text{；}}\end{array}\\[35pt]{0,{p_k}{\rm{ {\text{＞}} }} {b_k}/(2{a_k})}{\text{。}}\end{array}} \right.$

(12)

第2步：将(Q_rk )^*和D_rk 代入式(6)，由于 ${\text{∂} ^2}{\rm{TC}}{{\rm{M}}_r}/\text{∂} {({\lambda _{mrk}})^2} {\text{＞}} 0$ ，确定式(6)单调，利用一阶导数方程 $\text{∂} {\rm{TC}}{{\rm{M}}_r}/\text{∂} {\lambda _{mrk}} = 0$ 得出 $\lambda _{mrk}^*$ ，用所有的(Q_rk )^*、D_rk 和 $\lambda _{mrk}^*$ 计算出TCM。

第3步：将(Q_rk )^*、D_rk 和 $\lambda _{mrk}^*$ 代入式(7)， ${\text{∂} ^2}{\rm{TC}}{{\rm{S}}_s}/\text{∂} {({\lambda _{srk}})^2} {\text{＞}} 0$ ，同样的方法计算出 $\lambda _{srk}^*$ 、(Q_rk )^*、D_rk 、 $\lambda _{mrk}^*$ 与TCS。

第4步：将TCB、TCM、TCS加和得出非协调决策系统总成本TC。

4.2 基于启发式的协调决策模型求解

模型(9)是制造商协调零售商共同订货周期T的函数，由模型特性可运用启发式迭代，本文在求解时设定步长为0.2，求解过程如下。

第1步： ${\lambda _{srk = 1}} = {\lambda _{srk = 2}} = \cdots = {\lambda _{srk = g}} = {\lambda _{mrk}} = 1$ ，与其他参数值一并代入式(10)中，得出零售商共同订货周期 ${T^*} = T({\lambda _{srk = 1}},{\lambda _{srk = 2}}, \cdots ,{\lambda _{srk = g}},{\lambda _{mrk}})$ 。

第2步：将T^*代入式(9)，设 ${\rm{T}}{{\rm{C}}_1}({\lambda _{srk = 1}} = {\lambda _{srk = 2}} = $ $ \cdots = {\lambda _{mrk}}) = {\rm{T}}{{\rm{C}}_1}(1,1, \cdots ,1,1) = {\rm{T}}{{\rm{C}}_1}$ 。

第3步：设λ_mrk =1.2，将 ${\lambda _{srk = 1}} = {\lambda _{srk = 2}} = \cdots = {\lambda _{srk = g}} =$ $ 1$ ，λ_mrk =1.2代入式(10)，得出新T^*的值代入式(9)，得出 ${\rm{T}}{{\rm{C}}_1}({\lambda _{srk = 1}},{\lambda _{srk = 2}}, \cdots ,{\lambda _{srk = g}},{\lambda _{mrk}}) ={\rm{T}}{{\rm{C}}_1}(1,1, \cdots , $ $ 1,1.2) = {\rm{T}}{{\rm{C}}_2}$ 。

第4步：如果TC₁＜TC₂，则 ${\lambda _{srk = 1}} = {\lambda _{srk = 2}} = \cdots =$ $ {\lambda _{srk = g}} = 1,1, \cdots ,1,1$ ，及T^*是所求解的最优值。否则重新赋值，设λ_mrk =1.4，令 ${\rm{T}}{{\rm{C}}_1}(1,1, \cdots ,1,1.2) = {\rm{T}}{{\rm{C}}_1}$ ，通过式(10)再计算 ${\rm{T}}{{\rm{C}}_1}(1,1, \cdots ,1,1.4) = {\rm{T}}{{\rm{C}}_2}$ ，重新比较TC₁与TC₂，直到找出使 ${\rm{T}}{{\rm{C}}_1}(1,1, \cdots ,1,\lambda _{mrk}^*) {\text{＜}} $ ${\rm{T}}{{\rm{C}}_1}(1,1, \cdots ,1,\lambda _{mrk}^* + 0.2)$ 且 $ {\text{＜}} {\rm{T}}{{\rm{C}}_1}(1,1, \cdots ,1,\lambda _{mrk}^* - 0.2)$ 成立的 $\lambda _{mrk}^*$ ，即制造商最优的生产倍数，此步骤重复r×k次，找到所有的 $\lambda _{mrk}^*$ 。

第5步：令 ${\rm{T}}{{\rm{C}}_1}(1,1, \cdots ,1,\lambda _{mrk}^*) = {\rm{T}}{{\rm{C}}_1}$ ，设定供应商1的备货倍数为1.2，其他均为1，代入式(10)，得出 ${\rm{T}}{{\rm{C}}_1}(1.2,1, \cdots ,1,\lambda _{mrk}^*) = {\rm{T}}{{\rm{C}}_2}$ ，并与TC₁进行比较，重复上述1～4步，直到找出使 ${\rm{T}}{{\rm{C}}_1}(1.2,1, \cdots ,1,\lambda _{mrk}^* - 0.2) {\text{＞}} $ ${\rm{T}}{{\rm{C}}_1}(1.2,1, \cdots ,1,\lambda _{mrk}^*) {\text{＜}} {\rm{T}}{{\rm{C}}_1}(1.2,1, \cdots ,1,\lambda _{mrk}^* + 0.2)$ 都成立的 $\lambda _{srk = 1}^*$ ，即为供应商1的最佳备货倍数，此步骤重复g×r×k次，得出全部供应商的最佳备货倍数。

5 数值计算与分析 5.1 数值计算

三明化工厂和福建中闽化工是三农公司原材料供应商，草甘膦(产品1)主要3种原料由三明化工厂(S₁)供货，氯乙酸(产品2)所需2种原料来自中闽化工(S₂)，供应商相关参数见表1。

三农公司(m)每次生产启动成本S_m =20 000元，商品1、2的单位持有成本4元/件、2元/件，单位持有排放水平分别为2.5 kg/件、1.5 kg/件，生产2种产品的单位成本37元、16元，单位碳排放水平为22 kg与7 kg，原材料相关输入参数见表2。

公司在厦门、龙岩、南平三市设有代理机构，三个市场上草甘膦的销售价格分别205、190、185元/件(6 kg装)，氯乙酸的价格为102、128、88元/件(10 kg装)，零售商其他参数见表3。为简化计算，假设两种产品的需求参数相同，a=0.15，b=1.2，c=6，各成员分配碳额度(t)为C_r1=7 000，C_r2=8 000，C_r3=6 000，C_m =40 000，C_s1=11 000，C_s2=6 000，P=100元/t。按照4.1节求解步骤，得出非协调决策下供应链决策结果。当制造商协调统一订货，计算零售商协调订货周期为0.152，两种决策结果见表4～表6。

对比表4与表5，当供应链协调决策以后，无论是订货数量，还是生产倍数都明显降低。因此，表6中制造商协调零售商订货后，供应链各成员的运营成本大幅下降。

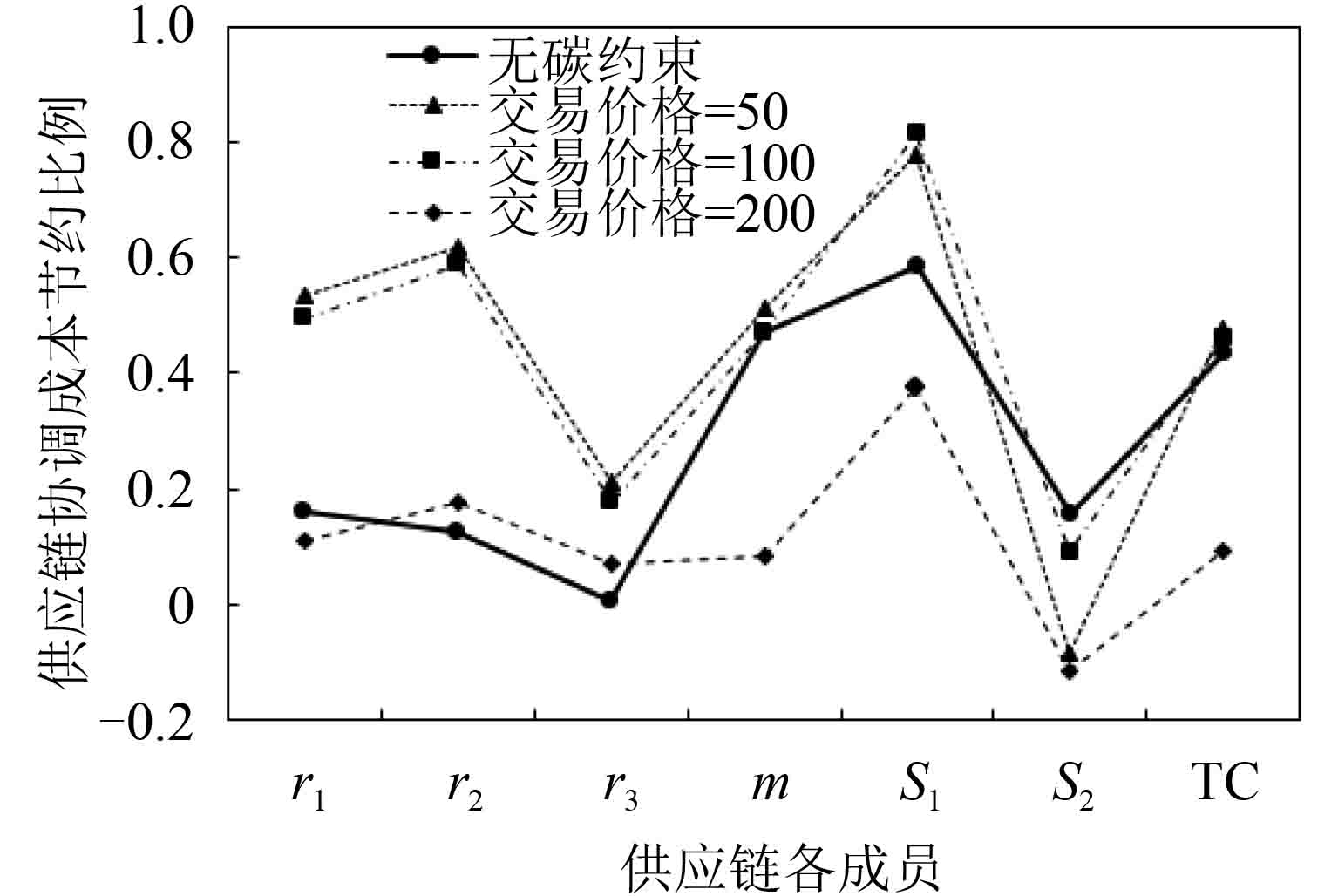
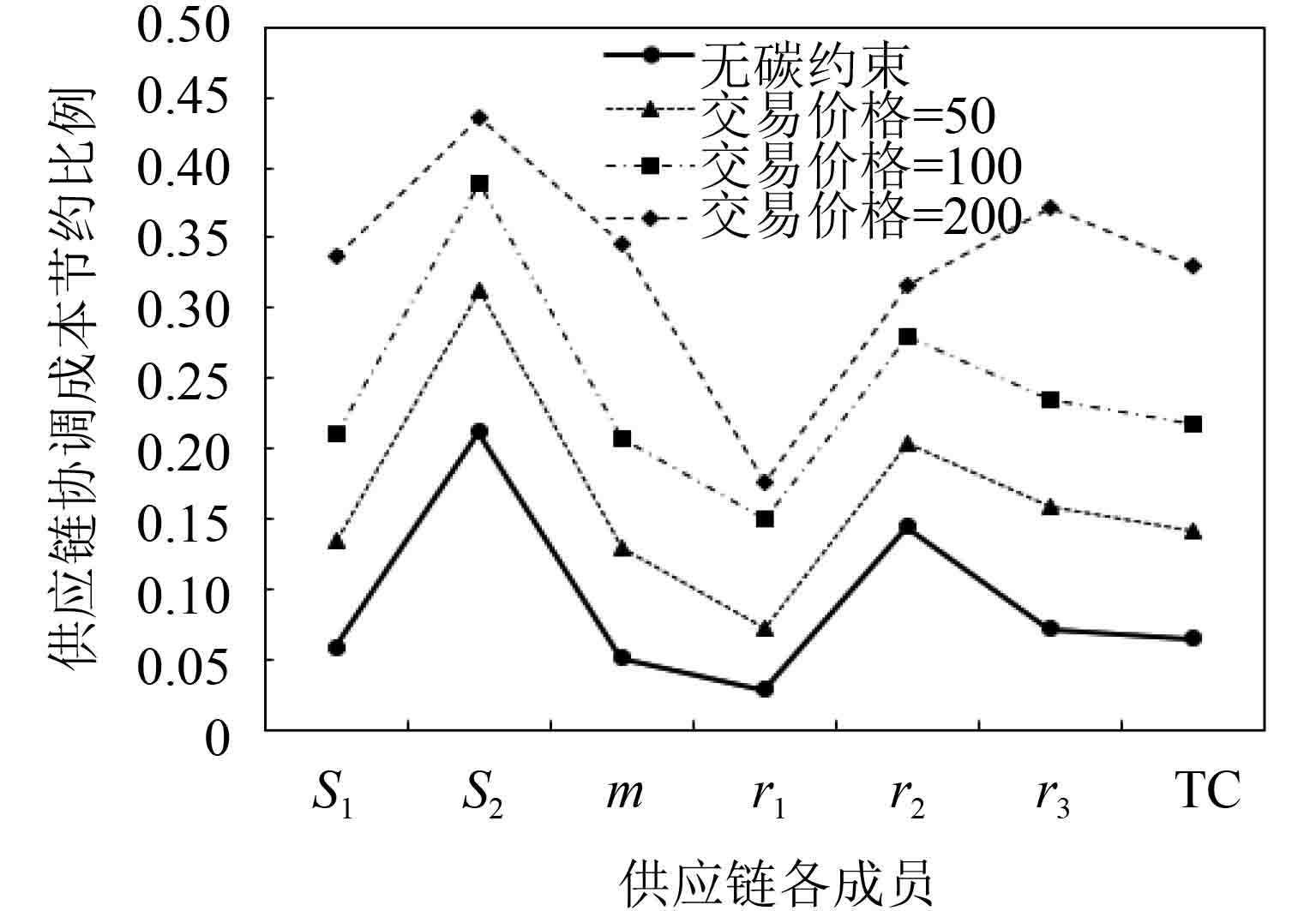
5.2 供应链协调效率与成本补偿分析

碳交易价格P=0，视为无碳约束情景，作为供应链协调效率基础，以节约比例γ表示协调效率，γ=(非协调结果–协调结果)/协调结果，各成员γ值联结，得出供应链成本与碳足迹协调效率曲线，如图1与图2所示。

图中实线代表无碳约束时，供应链的成本协调效率较低，然而当碳交易价格等于50时，制造商的成本协调效率最高。

从图中明显看到，当碳交易价格等于200时，供应链碳足迹的协调效率最高。

为了激励成员合作，参考Lee等^[13]的方法对协调后的成本进行二次分配，不改变各成员在独立决策时的相对地位。令ξ表示非协调运营下各成员成本比例，以协调成本4 020 305为分配标准，重新计算各成员成本TC₂(见表7)，∆₁表示制造商协调成本与二次分配成本差额，此时供应商2是成本分配的最大受益者，其成本降低74 197元，此外零售商3成本下降26 352元，从∆₂结果可以看出，相比于非协调成本TC，重新分配后的TC₂，每位成员都有成本节余，二次分配方案更利于协调达成。

5.3 碳足迹敏感性分析

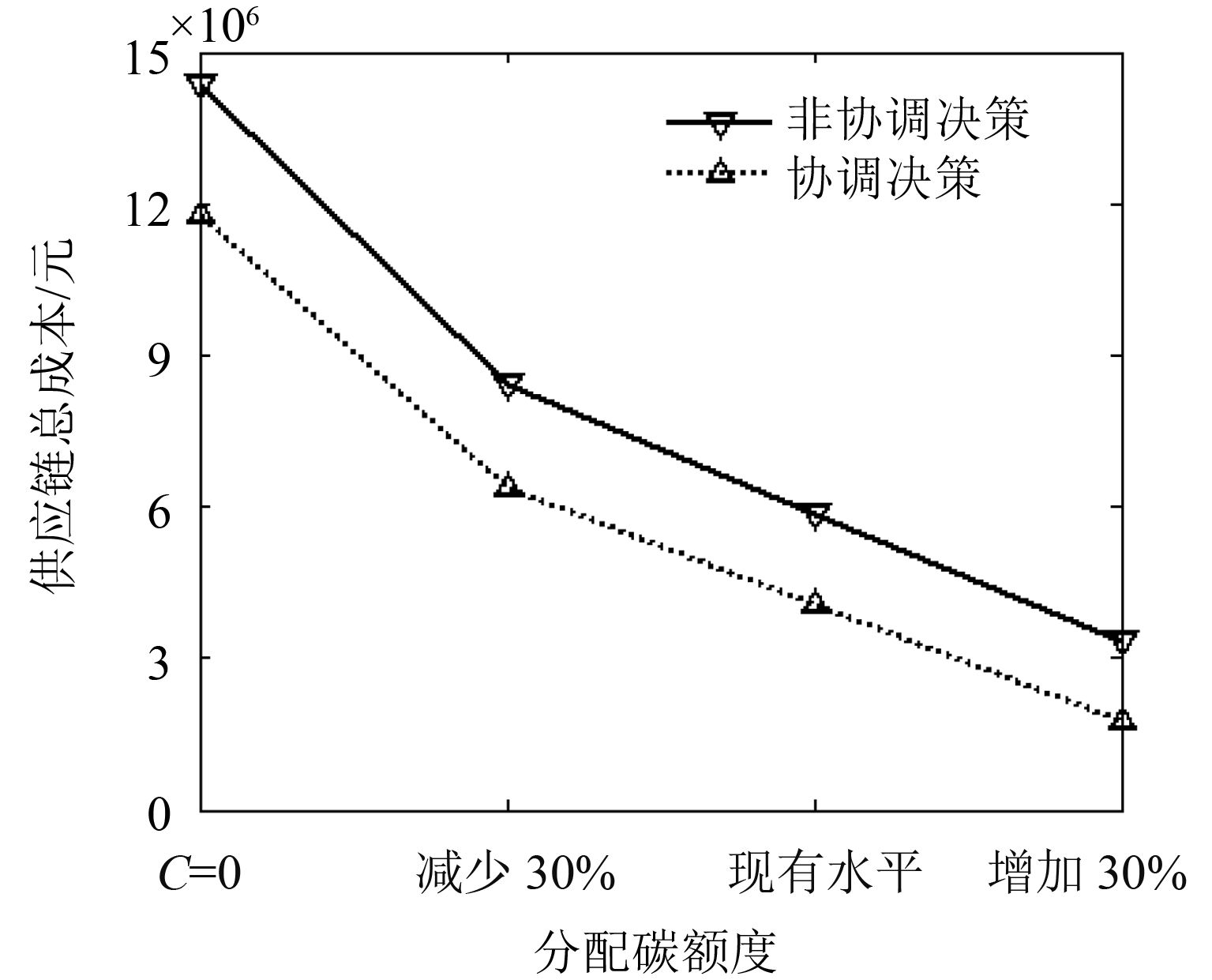
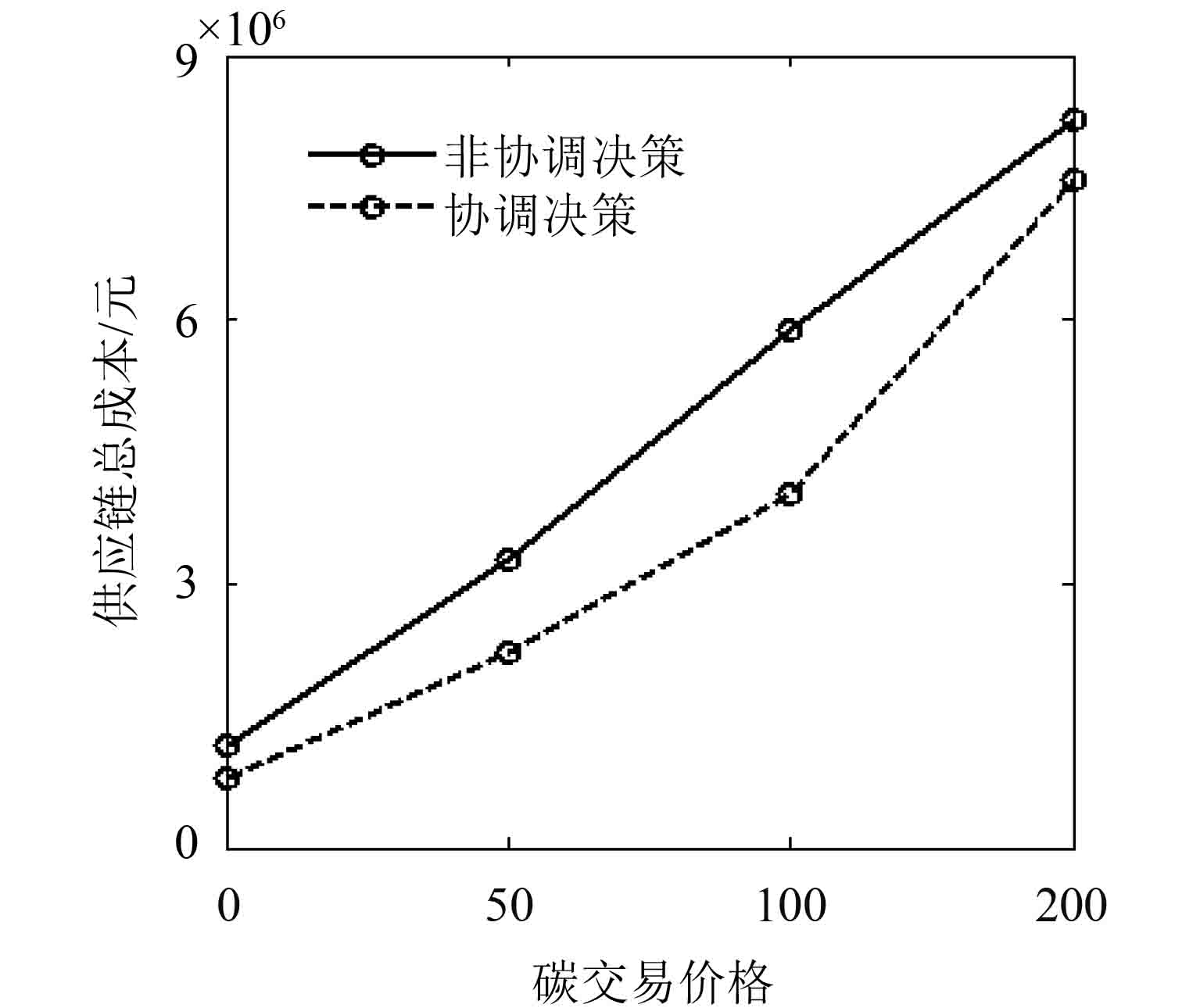
本文从政策调控与市场交易两个视角进行分析，在现行交易价格(P=100)之下，政府分配碳额度有4种变化趋势：1)C=0，即全部碳排放都要付费；2)减少30%；3)保持不变；4)增加30%，分配额度盈余或不足衍生出碳排放权交易市场。而在给定分配额度下，碳交易价格分别为：1)P=0，无偿取得碳配额；2)偏低P=50；3)正常价格P=100；4)偏高P=200。首先，碳分配额度、碳交易价格变化时供应链总成本变化趋势如图3与图4所示。

图3表明碳分配额度与总成本反向变化趋势，当分配额C=0，不存在免费配额时，供应链总成本最高。图4说明碳交易价格与总成本变化方向相同。而供应链碳足迹变化趋势如图5与图6所示。

图5表明碳分配额度增减不会影响供应链碳足迹，这与前面的结论相同。然而，在图6中，碳交易价格高低对碳足迹影响显著，供应链获得的全部配额为78 000 t，当交易价格P=200时，协调决策碳足迹为70 400 t，高交易价格下反而出现碳配额结余。

碳因素变化有2种特殊情景：分配碳额度C=0与碳交易价格P=0，前者视为最严厉的控排政策；后者表示，碳足迹约束失效。供应链成本与碳足迹变化如图7与图8。

对比图7与图8，碳交易价格P=0时，各成员成本水平最低，此时供应链碳足迹最高；相反，当碳分配额度C=0，成本急剧上升，而供应链碳足迹下降，出现了供应链成本与碳足迹的背反问题，相比之下，现有分配水平更可行。

通过上述分析得出：碳分配额度与碳交易价格增减变化都会影响决策变量及供应链运行成本，但二者相比，碳交易价格变动对供应链决策影响更显著。如果政府分配额度过高，其约束能力必然减弱，而过于严厉排控政策，无疑会增加企业负担；碳交易价格由市场供求决定，这取决于每个企业交易额度，高效节能企业更可能在碳配额转让中受益。

6 结论

当企业碳排放不再免费“搭便车”以后，碳足迹将直接影响企业运营。本文分析得出如下结论。1)在确定的碳交易价格之下，政府免费分配额度越高，供应链总成本越低，对其他决策变量没有影响。2)当供应链转化为制造商协调决策以后，供应链不仅出现成本节约，而且碳足迹减少，成本二次分配使供应链协调运作成为可能。3)在碳分配额度与碳交易价格两种极端变化情景下，供应链的碳足迹与运行成本此消彼涨，碳分配额度升高，供应链成本降低，而碳足迹将大幅提升，这与环境友好相悖。所以，部分免费配额，结合碳交易市场补充作用是碳排放控制初期的选择，价格机制是更有利的控排杠杆。

随着环保理念的深入，低碳供应链将越来越被公众接受与认可。碳足迹下供应链的协调机制、供应链系统的定价机制、成员间的碳交易机制都是未来可能的研究方向。