2. 青岛大学 数学与统计学院,山东青岛 266071;
3. IBM中国上海研究院,上海 201203;
4. 上海财经大学 信息管理与工程学院,上海 200433
2. School of Mathematics and Statistics, Qingdao University, Qingdao 266071, China;
3. IBM China Research Laboratory, Shanghai 201203, China;
4. School of Information Management and Engineering, Shanghai University of Finance and Economics, Shanghai 200433, China
智能电网是采用先进的智能计量设施和通信技术来检测和测量用户电力消耗的新型电力系统[1],能够使电力生产的发电、配电和用电更加高效、经济、可靠[2]。需求响应管理是解决日益增长电力需求的智能电网的一个关键解决方案,可以避免发电基础设施过多投资,帮助用户提高电力利用效率,降低成本[3-5],减少电力消耗峰值时间以及平衡电力供给和需求[6-7]。DRM的经典文献可参见[8-11]。
智能定价作为DRM的一种方式,是鼓励用户更加智能和有效使用电力的手段。已有智能定价方法包括实时电价(real-time pricing, RTP),分时电价(time-of-use pricing, TOUP),和日前电价(day ahead pricing, DAP)[7,12-13]等,其中最重要的是实时电价。国内外关于实时电价的研究主要体现在以下几个方面:首先,研究涉及到用户如何对实时电价进行自动响应,以较低费用达到理想满意程度[6];其次,研究实时电价如何由电力零售商制定,而不考虑用户对预测价格的潜在反应[14-15];第三,研究整个社会福利最大化的电力供需匹配问题[7-8,16];最后,应用博弈方法研究实时电价,如文献[6]通过在用户中生成一个n人具有凹性的非合作博弈来研究RTP问题,进而获得分布式DRM策略以使电力成本最小化。文献[17]提出了基于网络拥塞博弈的负荷管理策略来讨论RTP问题。文献[18]则在电力零售商之间建立Stackelberg博弈模型分析RTP问题。上述应用博弈方法研究实时电价的工作都是考虑用户之间或电力供应商之间的竞争来讨论实时电价问题,而现实中面对的挑战则是电力系统呈现出的多层次结构,如文献[19]将电力零售商与用户之间的策略互动视为统一形式生成Stackelberg博弈研究RTP问题。实际上多个电力零售商和多个用户是智能电网下开放电力市场的一种普遍现象[11],文献[20]中具有多个电力供应商和多个家庭住宅用户的DRM问题被模型为一个二层博弈问题进行研究,文献[21]与[20]类似,也将供应商和用户端分别建立非合作博弈研究DRM问题,然而文献[20]和[21]都未考虑电力供应商和用户之间的竞争。在文献[22]中,在仅具有局部信息情形下,基于Stackelberg博弈的RTP问题被研究并获得一些有意义的结果。
本文通过分析电力零售商和用户之间的策略互动行为来研究智能电网下的实时电价问题。不同于文献[20-22]的是:首先,使用更具有一般意义的二次效用函数来描述用户的偏好行为,并且博弈是在零售市场中的多个电力零售商和多个用户之间进行;另外,既然需求响应行为中最常见方式是价格响应和激励机制,而有效激励市场从传统的固定价格机制向实时定价机制转换方式是提供货币激励,因此设计一种由电力零售商提供激励因子的方法来调整用户的用电行为,以便维护电力系统供需平衡和稳定运行。最后,设计了新的求解实时电价的分布式算法。
1 系统模型考虑一个由多个电力零售商和多个用户组成的智能电网系统,M={1, 2,…,m}表示电力零售商集合,用户集合用N={1, 2,…,n}表示。各个零售商从电力批发市场购买电力然后将其卖给用户。用户安装有EMC(energy management controller)来通过双向联通网络与零售商进行实时互动,合理安排电力使用。于是电力零售商和用户之间能够通过双向联通交流电力实时价格和需求信息,其中用户费用和电力零售商投资约束也被考虑。
假设一个运行时间循环被分成K个时间区间,每个时间区间k(k∈{1,2,…,K})中,电力零售商接受用户的电力需求信息并将实时价格发送给用户的EMC,通常取K=24,即每个时间区间为1 h。用
与文献[7]、[9]、[14]、 [19]类似,本文研究的实时电价问题是基于日前24 h电价数据进行建模求解,每一时刻计算方式相同,因此在以下建模分析过程中以一个时刻进行。
1.1 激励因子的引入在放松管制的电力市场多个电力零售商共存,零售商们通过调整实时电价相互竞争以最大化自己收益,同时根据用户的消费模式以及偏好,基于用户的需求响应采用多种激励机制。本文零售商根据用户的电力消费行为来提供贴现进行激励以保持并赢得更多用户,这里的贴现不一定是为了给用户带来明显的现金补贴,也可以是为了给用户带来满意度的提高和效用的增加,从而促使用户更积极地参与到需求响应中来。不同零售商设定的激励贴现因子不同,不妨设零售商j额度设为ωj
元/单位电量,即当用户i电力消耗为
在电力市场中,用户消费电力情形不尽相同,其行为可用微观经济学中具有递减边际收益的效用函数进行描述来表示用户的满意度水平。用户效用函数可由一个二次函数[5]或对数函数[14,23]进行模拟是因为其具有以下2个特征:首先,它是关于电力消费量的凹函数;第二,每个用户的相应电力需求函数是单调不减的。因此,本文依然沿用二次函数形式的效用函数,则用户i从电力零售商j处消费电量为xij 后的效用函数为
| $\quad\quad {u_i}\left( {{x_{ij}},{X_i}} \right) = \left\{ \begin{aligned}{X_i}{x_{ij}} - \frac{{\textit{α}} }{2}x_{ij}^2,0 {\text{≤}} {x_{ij}} {\text{≤}} \frac{{{X_i}}}{{\textit{α}} }\text{;}\\\frac{{X_i^2}}{{2{\textit{α}} }}\text{,}{x_{ij}} {\text{≥}} \frac{{{X_i}}}{{\textit{α}} }\text{。}\quad \ \end{aligned} \right.$ | (1) |
这里Xi >0为随用户与时间不同而不同参数,代表用户增加消费电力的意愿,0<α≤1为事先给定的参数,xij 表示用户i从零售商j处消耗的电力实时需求,可以设定适当的参数比如较大的Xi 和较小的α来反映用户较高电力需求,pj 为电力零售商j提供的电力价格。当然,假定用户的电力需求可以根据电力消耗的历史数据来准确预测。
既然每个用户可以选择多个电力零售商作为电力供应商,并能获得来自电力零售商的激励贴现。于是用户i的总福利函数为
| $\begin{split} & \quad\quad {U_i}\left( {{p_j},{x_{ij}}} \right) = \sum\limits_{j \in M} {\left[ {{u_i}\left( {{x_{ij}},{X_i}} \right) - {p_i}{x_{ij}} + {w_j}{x_{ij}}} \right]} = \\ & \sum\limits_{j \in M} {\left[ {\left( {{X_i} - {p_j} + {w_j}} \right){x_{ij}} - \frac{\alpha }{2}x_{ij}^2} \right]\text{。}} \end{split}$ | (2) |
电力零售商j的成本函数为其提供的实时电力需求的函数,表示为
| $\quad\quad {L_j} = p\sum\limits_{i \in N} {{x_{ij}}}\text{。} $ | (3) |
其中,p为电力零售商j采购于电力批发市场中电力的价格,这里设为常数。电力市场中每个电力零售商j对用户报价可依据用户需求响应及其他零售商报价做出最优反应并给出激励,故零售商j利润函数为
| $\quad\quad {R_j}\left( {p} \right) = \left( {{p_j} - p - {w_j}} \right)\sum\limits_{i \in N} {{x_{ij}}}\text{。}$ | (4) |
用户的主要目标是以较低的价格购买较多电量获得更高福利,反之,从电力零售商的角度来看,他们的目标是以制定更高的电力零售价格实现更高的收入。因此,应制定适当的实时定价策略来使零售商端和用户端保持电力需求供应平衡。
本文主要关注电力零售商与其服务终端用户之间的策略互动对于电力市场影响,与传统完全竞争的电力市场中市场参与者没有能力通过其个人行为影响市场价格所不同,本文中的多个电力零售商在电力市场中相互之间竞争进行非合作博弈。
当制定不同价格的多个零售商在电力市场中共存时,对每个用户而言选择不同零售商购电成本自然不同,当然一个零售商制定电价也受其他零售商电价影响。所有零售商制定电价并将其公告给用户后,用户对价格向量做出最优反应,选择电力零售商并确定从其购买自己所需最优电量。由于零售商和用户的策略行为是顺序进行,因此将零售商和用户之间的策略互动行为模型为一个Stackelberg博弈[24]。该模型实际上是一个多领导者和多跟随者Stackelberg博弈。用户的实时电力需求依赖于电力零售商的电价和他们自己的电力成本约束。反之,零售商则根据用户的电力需求反应来优化自己的实时电价。另外在电力用户之间也由于选择零售商购买电力而产生竞争。因此,在电力零售商端和用户端的竞争都被建模为博弈模型。
2.1 用户侧分析在智能电网中,每个用户都是最大化自己福利的理性消费者,用Ci 表示用户i购买电力的预算,则对于给定的所有零售商的报价向量集合(p1,…,pj ,…,pm ),用户i对其做出最优反应使自己福利最大化,即为求解以下优化问题
| $\left\{ \begin{array}{l}\mathop {\max }\limits_{{X_i}:\left\{ {{x_{ij}},\forall j \in M} \right\}} {U_i} = \sum\limits_{j = 1}^m {\left[ {\left( {{X_i} - {p_j} + {w_j}} \right){x_{ij}} - \frac{\alpha }{2}x_{ij}^2} \right]} {{\text{。}}}\\[10pt]{\rm{s}}.{\rm{t}}.\sum\limits_{j \in M} {p_j}{\text{≤}}{x_{ij}}{C_i}{{\text{,}}}\ \ {x_{ij}}{\text{≤}}0,\forall j \in M{{\text{。}}}\end{array} \right.$ | (5) |
上述优化问题是一个凸优化问题,其解唯一存在且全局最优。下面首先从2家电力零售商开始讨论,用户i优化问题为
| $\left\{ \begin{array}{l}\displaystyle\mathop {\max }\limits_{{X_i}:\left\{ {{x_{i1}},{x_{i2}}} \right\}} {U_i} = \sum\limits_{j = 1}^2 {\left[ {\left( {{X_i} - {p_j} + {w_j}} \right){x_{ij}} - \frac{\alpha }{2}x_{ij}^2} \right]} = \\ \!-\! \displaystyle\frac{\alpha }{2}x_{i1}^2 \!-\! \frac{\alpha }{2}x_{i2}^2 \!+\! \left( {{X_i} \!-\! {p_1} \!+\! {w_1}} \right){x_{i1}} \!+\! \left( {{X_i} \!-\! {p_2} \!+\! {w_2}} \right){x_{i2}}{{\text{。}}}\\[8pt]{\rm{s}}{\rm{.t}}{\rm{.}} \ \ {p_1}{x_{i1}} + {p_2}{x_{i2}}{\text{≤}}{C_i}, \ {x_{i1}},{x_{i2}}{\text{≥}}0{{\text{。}}}\end{array} \right.$ | (6) |
通过引入拉格朗日乘子将上述优化问题转化,构造拉格朗日函数为
| $\begin{split}& {L_i} \!\!=\!\! \sum\limits_{j = 1}^2 {\left[ {\left( {{X_i} - {p_j} + {w_j}} \right){x_{ij}} - \frac{\alpha }{2}x_{ij}^2} \right]} - {\lambda _{i1}}\left( {\sum\limits_{j = 1}^2 {{p_j}{x_{ij}} - {C_i}} } \right) \!\!+ \\& {\lambda _{i2}}{x_{i1}} + {\lambda _{i3}}{x_{i2}} \text{。}\end{split}$ | (7) |
其互补松驰条件为
| $\quad \quad {\lambda _{i1}}\left( {{p_1}{x_{i1}} + {p_2}{x_{i2}} - {C_i}} \right) = 0\text{,}$ | (8) |
| $\quad\quad {\lambda _{i2}}{x_{i1}} = 0\text{,}$ | (9) |
| $\quad\quad{\lambda _{i3}}{x_{i2}} = 0\text{,}$ | (10) |
| $\quad\quad{\lambda _{i1}} {\text{>}} 0,{\lambda _{i2}},{\lambda _{i3}},{x_{i1}},{x_{i2}} {\text{≥}}0\text{。} $ | (11) |
且上述优化问题的一阶最优性条件为
| $\quad\quad \left\{ \begin{array}{l} - \alpha {x_{i1}} + {X_i} - {p_1} + {w_1} - {\lambda _{i1}}{p_1} + {\lambda _{i2}} = 0,\\[5pt] - \alpha {x_{i2}} + {X_i} - {p_2} + {w_2} - {\lambda _{i1}}{p_2} + {\lambda _{i3}} = 0\text{。}\end{array} \right.$ | (12) |
以下分4种情形讨论。
1)xi1,xi2>0时,有λi2=λi3=0,代入式(12)可得
| $\quad\quad {x_{ij}} = \frac{{{X_i} - {p_j} + {w_j} - {\lambda _{i1}}{p_j}}}{\alpha },\forall i \in N,j = 1,2\text{。}$ | (13) |
在式(8)中使用式(13),可得
| $\quad\quad {\lambda _{i1}} = \frac{{\sum\limits_{j = 1}^2 {\left( {{X_i} + {w_j}} \right){p_j} - {C_i}\alpha } }}{{\sum\limits_{j = 1}^2 {p_j^2} }} - 1\text{。} $ | (14) |
再将其代回式(13),可得
| $ \quad \quad {x_{ij}} \!=\! \frac{{{X_i} \!+\! {w_j} \!- \!\!\left[\!\! {{p_j} \!\!\! \sum\limits_{j = 1}^2 \!\!{\left( {{X_i} \!+\!\! {w_j}} \right){p_j} \!-\! {C_i}\alpha {p_j}} }\!\! \right] \!\!\! / \!\!\sum\limits_{j \!\!=\!\! 1}^2 {p_j^2} }}{\alpha },j \! = \! 1,2\text{。}$ | (15) |
2) 若xi1>0,xi2=0时,此即第1种情形中xi2=0。而实际上根据xi1>0及式(9)有λi2=0,从而
| $\quad\quad {x_{i1}} = \frac{{{X_i} + {w_1} - \left( {1 + {\lambda _{i1}}} \right){p_j}}}{\alpha }\text{。}$ | (16) |
将式(16)代入式(8),得到
| $\quad\quad {\lambda _{i1}} = \frac{{\left( {{X_i} + {w_1}} \right){p_1} - {C_i}\alpha }}{{p_1^2}} - 1\text{。}$ | (17) |
再将其代入式(16)可得xi1=Ci /p1。又由第1种情形中xi2=0可以求出Ci 后,将其代入xi1=Ci /p1后可得
| $\quad\quad {x_{i1}} = \frac{{{C_i}}}{{{p_1}}} = \frac{{{X_i} + {w_1} - \left( {{X_i} + {w_2}} \right)\displaystyle\frac{{{p_1}}}{{{p_2}}}}}{\alpha }\text{。}$ | (18) |
事实上,将在第1种情形中得到的xi1代入Ci 后,同样可得式(18),故仍可得到
| ${x_{i1}} \!=\! \frac{{{X_i} \!+\! {w_1} \!-\! \left[ {{p_1}\sum\limits_{j = 1}^2 {\left( {{X_i} \!+\! {w_j}} \right){p_j} \!-\! {C_i}\alpha {p_1}} } \right] \!\! / \!\! \sum\limits_{j = 1}^2 {p_j^2} }}{\alpha } \!=\! \frac{{{C_i}}}{{{p_1}}} \text{。}$ | (19) |
3) 若xi1=0,xi2>0时,同2)可得
| ${x_{i2}} \!=\! \frac{{{X_i} \!+\! {w_2} \!-\! \left[ {{p_2}\sum\limits_{j = 1}^2 {\left( {{X_i} \!+\! {w_j}} \right){p_j} \!-\! {C_i}\alpha {p_2}} } \right]/\sum\limits_{j = 1}^2 {p_j^2} }}{\alpha } \!=\! \frac{{{C_i}}}{{{p_2}}} \text{。}$ | (20) |
4) 若xi1=xi2=0时,意味着用户的电力需求为0,这与现实情形不相符合。
综合上述几种情形并根据函数可知,对于给定m个零售商的报价向量集合(p1,…,pj ,…,pm ),每个用户用电量可被表示为
| $ \begin{split}& \quad \quad {x_{ij}} \!\!=\!\! \frac{{{X_i} \!+\! {w_j} \!-\! \left[ {{p_j}\!\sum\limits_{j = 1}^m {\left( {{X_i} \!+\! {w_j}} \right){p_j} \!-\! {C_i}\alpha {p_j}} } \right]\!/\!\sum\limits_{j = 1}^m\! {p_j^2} }}{\alpha },\\& \forall i \in N,j \in M \text{。}\end{split}$ | (21) |
同时,既然
| $\begin{split}& \quad\quad {p_j}\sum\limits_{j = 1}^m {\left( {{X_i} + {w_j}} \right){p_j} - {C_i}\alpha {p_j}} {\text{≤}} \left( {{X_i} + {w_j}} \right)\sum\limits_{j = 1}^m {p_j^2} ,\\& \alpha {\text{>}} 0,\forall i \in N,j \in M \text{。}\end{split}$ | (22) |
即
| $\quad\quad {p_j} \! {\text{≤}}\! \frac{{\left( {{X_i} + {w_j}} \right)\sum\limits_{j = 1}^m {p_j^2} }}{{\sum\limits_{j = 1}^m {\left( {{X_i} + {w_j}} \right){p_j} - {C_i}\alpha } }},\alpha {\text{>}} 0,\forall \! i \! \in \! N,j \in M \text{。}$ | (23) |
由于电力的不易储存特点,每个电力零售商目标是卖掉所有采购电量,由于零售商之间的竞争约束了随意抬高电价,因此零售商之间进行非合作定价博弈,对于一个零售商来说其最优化问题为
| $ \quad \mathop {\max }\limits_{p: = \left\{ {{p_j},\forall j \in M} \right\}} {R_j} = \left( {{p_j} - p - {w_j}} \right)\sum\limits_{i \in N} {{x_{ij}}} {{\text{。}}}$ | (24) |
| $\begin{split} \quad\quad{\rm{s}}{\rm{.t}}{\rm{.}}& \sum\limits_{i \in N} {{x_{ij}}} {\text{≤}} {P_j},\\& {p_j} {\text{>}} 0,\forall j \in M \text{。}\end{split}$ | (25) |
其中,Pj 为在电力批发市场采购电力总量。该问题是一个非线性优化问题,可采用拟牛顿等算法进行求解。
3 Stackelberg博弈模型 3.1 Stackelberg均衡电力零售商之间通过各自实时报价进行非合作博弈达到Nash均衡,并将均衡价格告知所有用户,而所有用户对电力零售商报价做出最优反应,从而生成Stackelberg博弈。
定义
1 令
| $\quad\quad {R_j}\left( {{p}*,{{x}}\left( {{p}*} \right)} \right) \! {\text{≥}} \! {R_j} \! \left( {{p_j},{p}_{ - j}^*,{{x}}\left( {{p_j},{p}_{ - j}^*} \right)} \right),\forall j \! \in \! M \text{。}$ | (26) |
这里
| $\quad\quad{{ {x}}_i}\left( {{p}*} \right) \!=\! \left\{ {{\varsigma _{_{U,i}}} \in {{\textit{Γ}} _{U,i}};{U_i}\left( {{p}*,{\varsigma _{_{U,i}}}} \right) \! {\text{≥}} \! {U_i}\left( {{p}*,{{ {x}}_i}} \right)} \right\},\forall i \in N \text{。}$ | (27) |
这里
给定价格向量 p ,对每个用户i求解最优化问题,式(21)可以得到唯一最优解,因此如果在电力零售商之间的定价博弈存在一个Nash均衡,则该Stackelberg博弈模型拥有一个Stackelberg均衡。
定理 1 电力零售商之间的定价博弈存在Nash均衡,于是Stackelberg博弈也存在Stackelberg均衡。
证明 所有电力零售商之间的定价博弈模型的策略空间为
电力零售商的价格信息是各自的隐私,传统的逆向归纳法难以求解,于是设计一个分布式算法进行求解。通过给每个电力零售商一个任意初始值pj,1来开始此算法过程,其后零售商们将初始价格向量告知用户,然后每个用户根据式(21)得出需要购买电量。零售商j的单位电价通过以下迭代公式进行更新
| $\quad\quad {p_{j,t + 1}} = {p_{j,t}} + \left( {\sum\limits_{i \in N} {{x_{ij,t}} - {P_j}} } \right)/{\sigma _j} \text{。}$ | (28) |
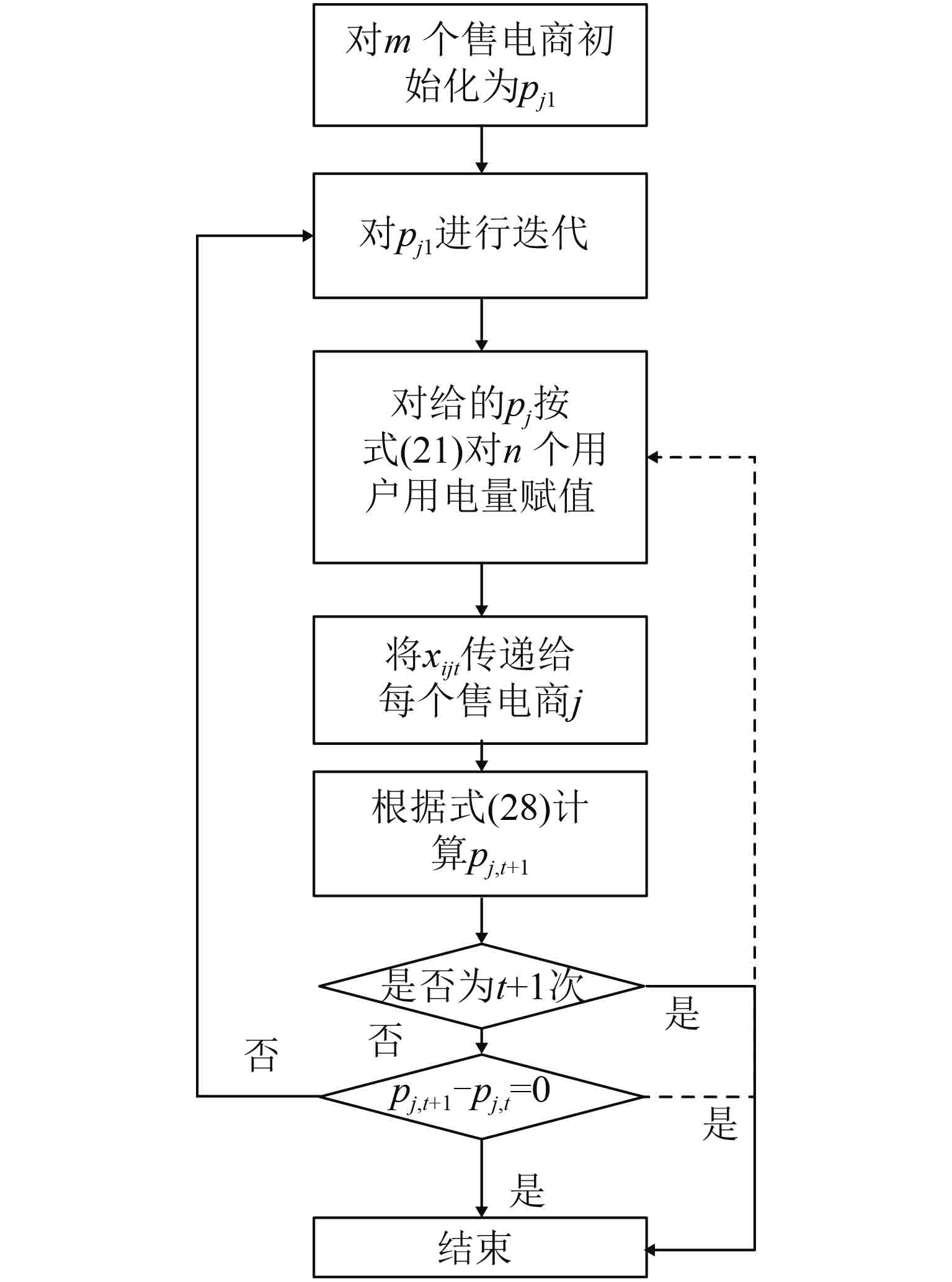
其中,t是迭代次数;σj 是零售商j迭代步长,通常被假设足够大。一旦零售商更新电价则立即将其信息传递给所有用户,然后所有用户更新电力需求并通告给电力零售商。当价格向量收敛时此过程终止,算法流程图如图1所示。
|
图 1 分布式算法流程 Fig. 1 Distributed algorithm flow chart |
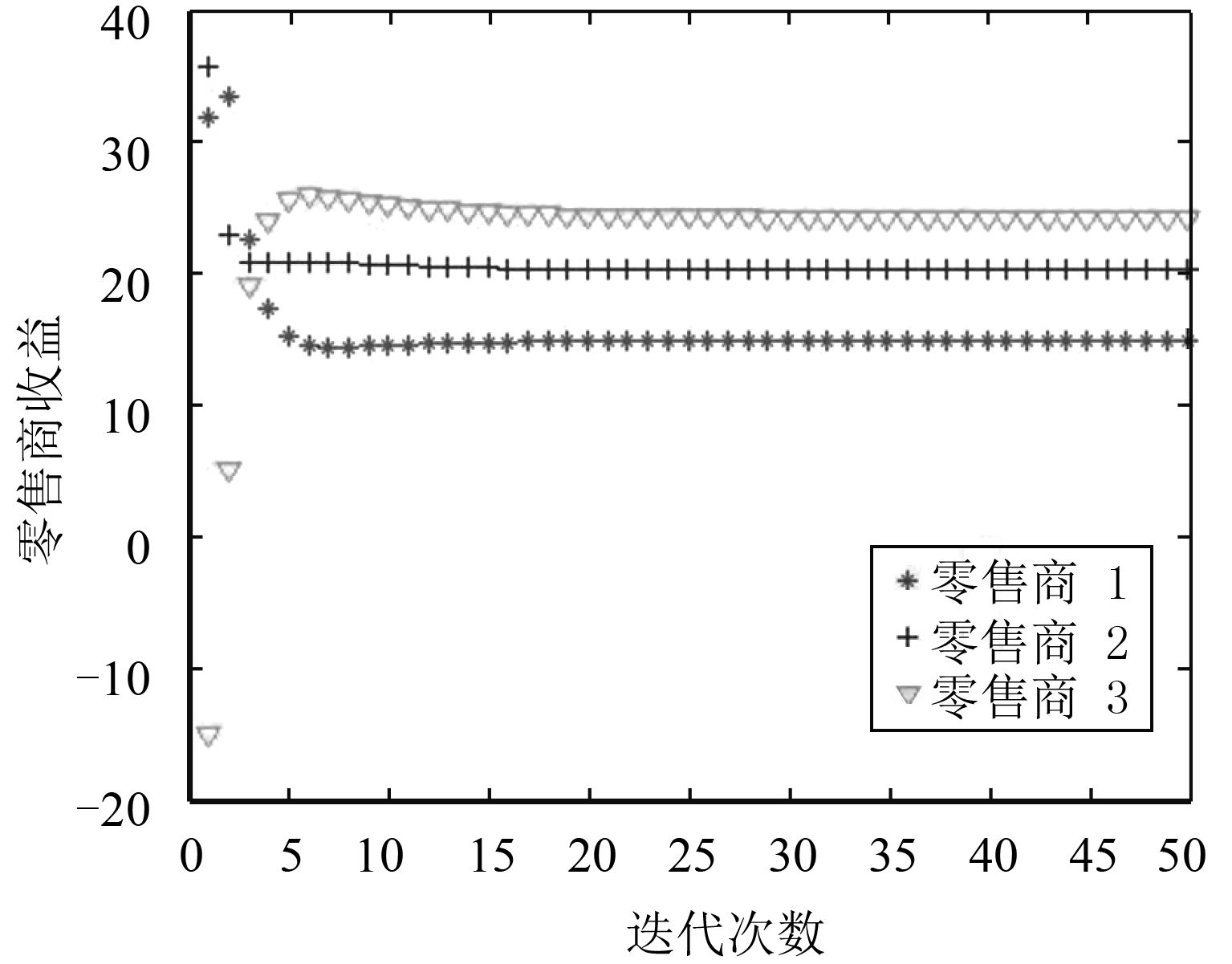
本节首先进行仿真来验证算法的收敛性,从而检验用户如何在零售商的单位价格向量基础上采取最优购买电力行为,而电力零售商则考虑如何在采购电力约束和用户购电费用约束基础上实时调整价格向量以使自己利润最大化。模拟过程中,考虑3个零售商和5个用户,参数分别设定为α=0.2,Xi =3(i=1, 2,…, 5),p=0.3,ωj =0.05,j=1, 2, 3。5个用户在一个时间段的成本约束分别为C1=5,C2=10,C3=15,C4=20,C5=25。所有零售商的采购电力的限制为P1=10,P2=15,P3=20,每个时隙设为1 h。接着再考虑激励因子带来的影响。
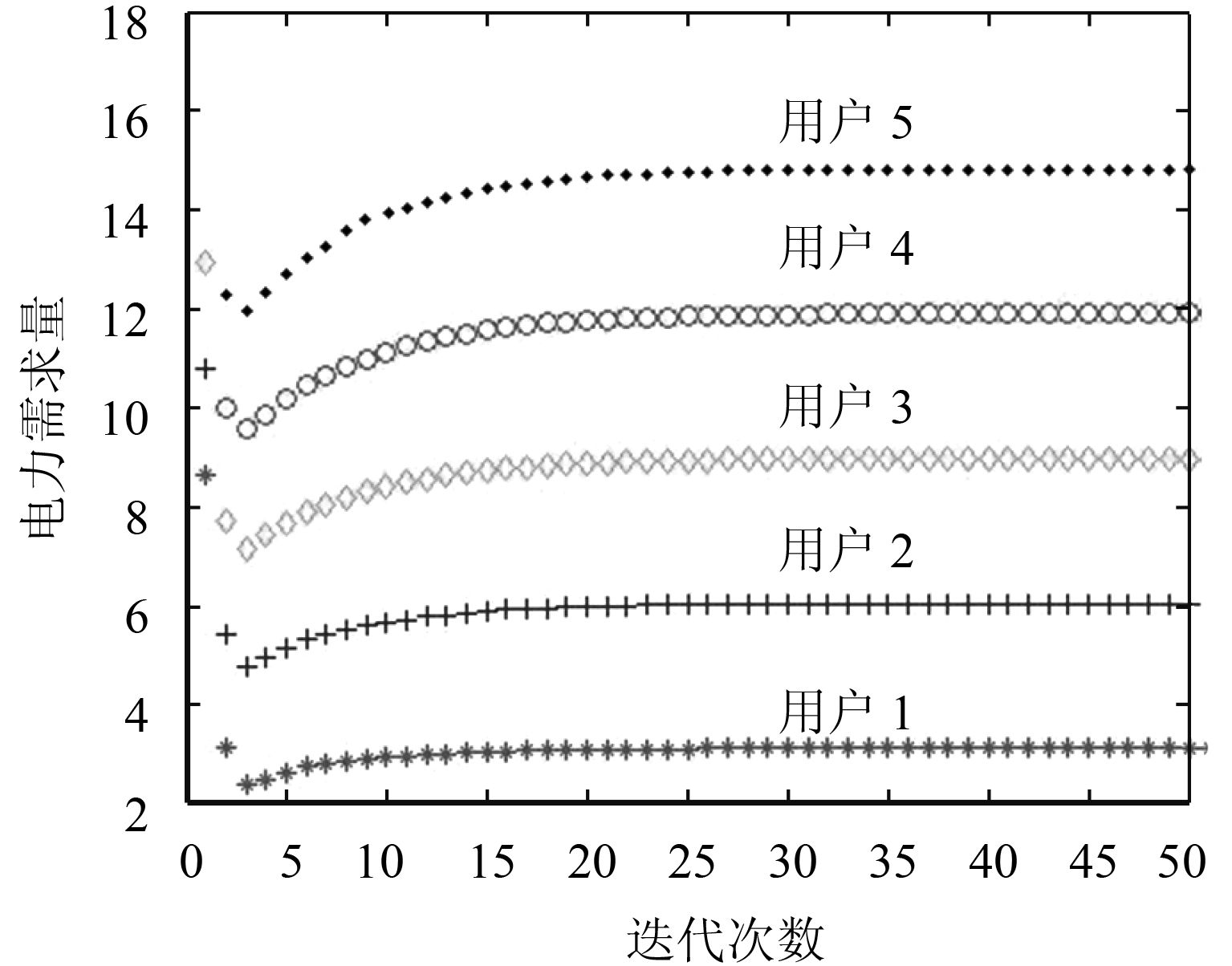
5.1 分布式算法图2~图5表明
|
图 2 分布式算法中用户的实时电力需求 Fig. 2 The real-time power demand of users in distributed algorithm |
|
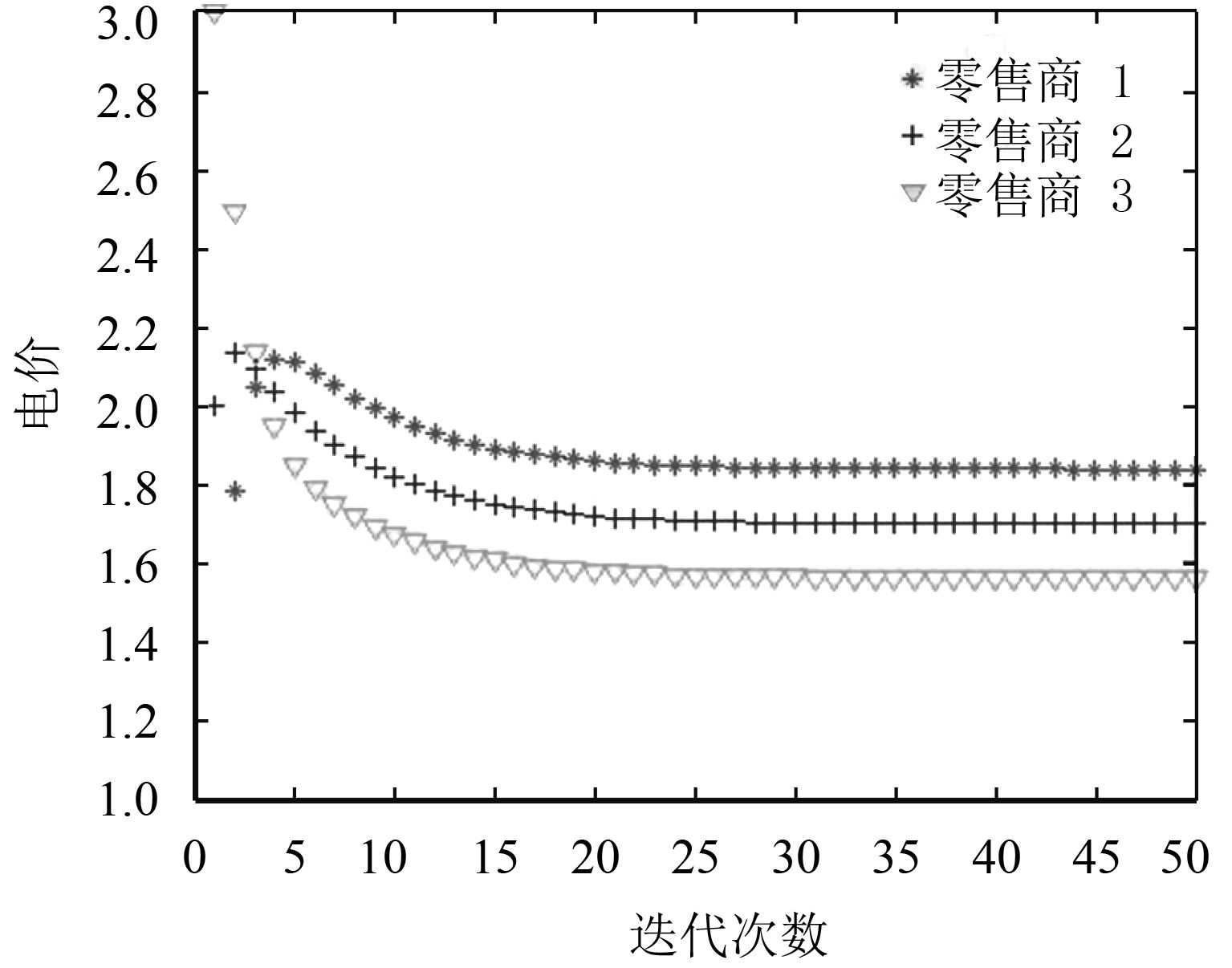
图 3 分布式算法中零售商的实时电价 Fig. 3 The real-time power price of retailers in distributed algorithm |
|
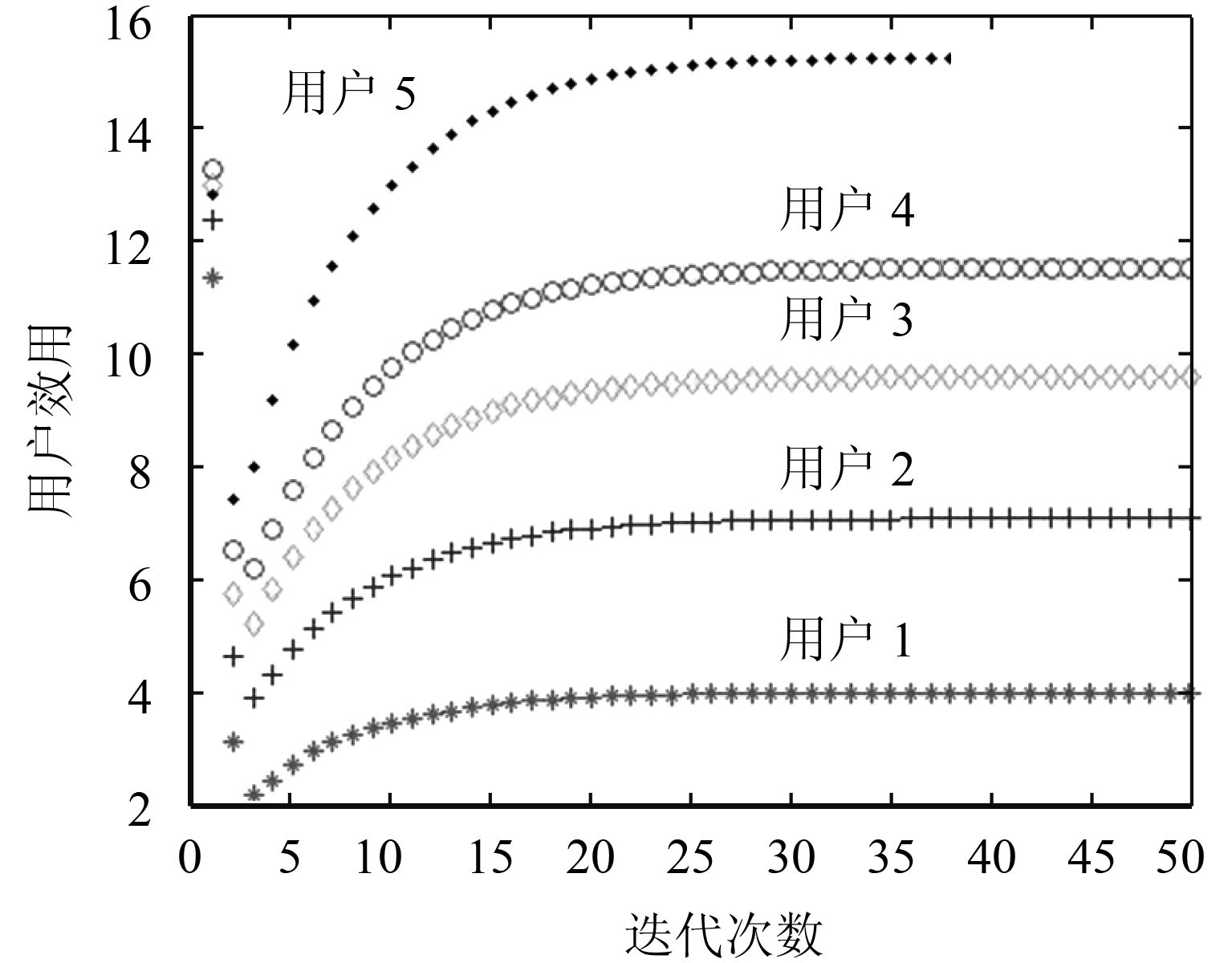
图 4 分布式算法中用户的效用 Fig. 4 The utilities of users in distributed algorithm |
|
图 5 分布式算法中零售商的收益 Fig. 5 The revenues of retailers in distributed algorithm |
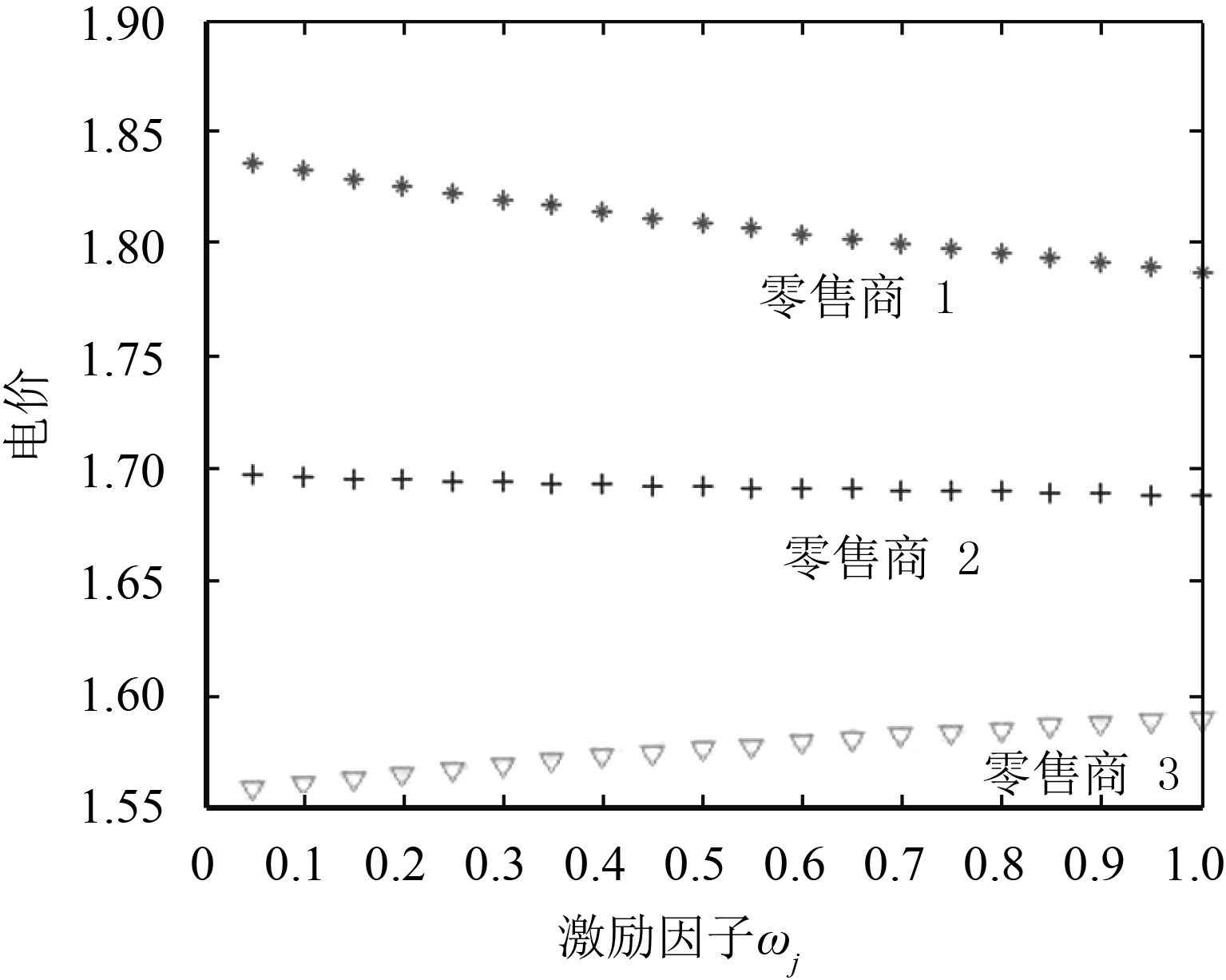
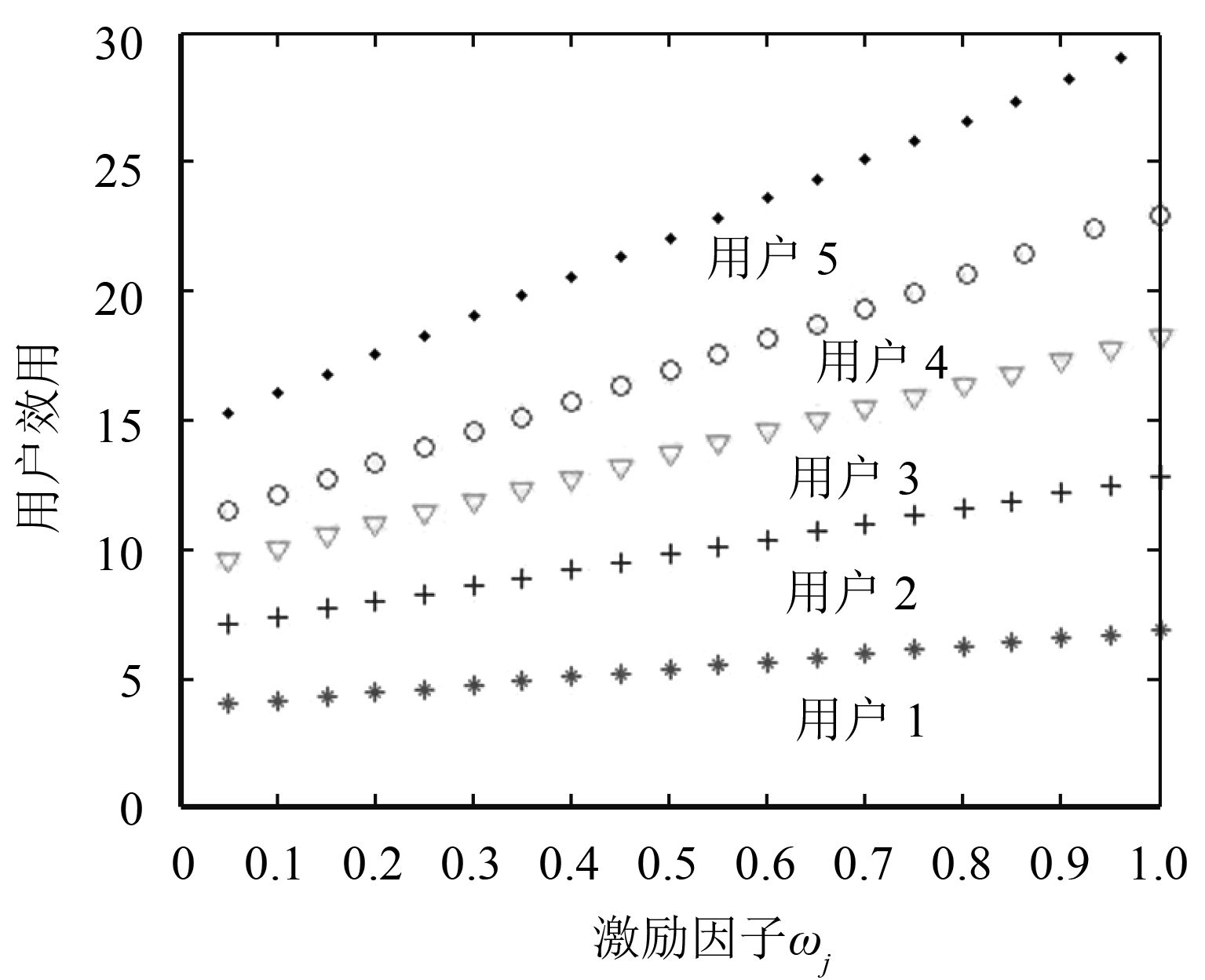
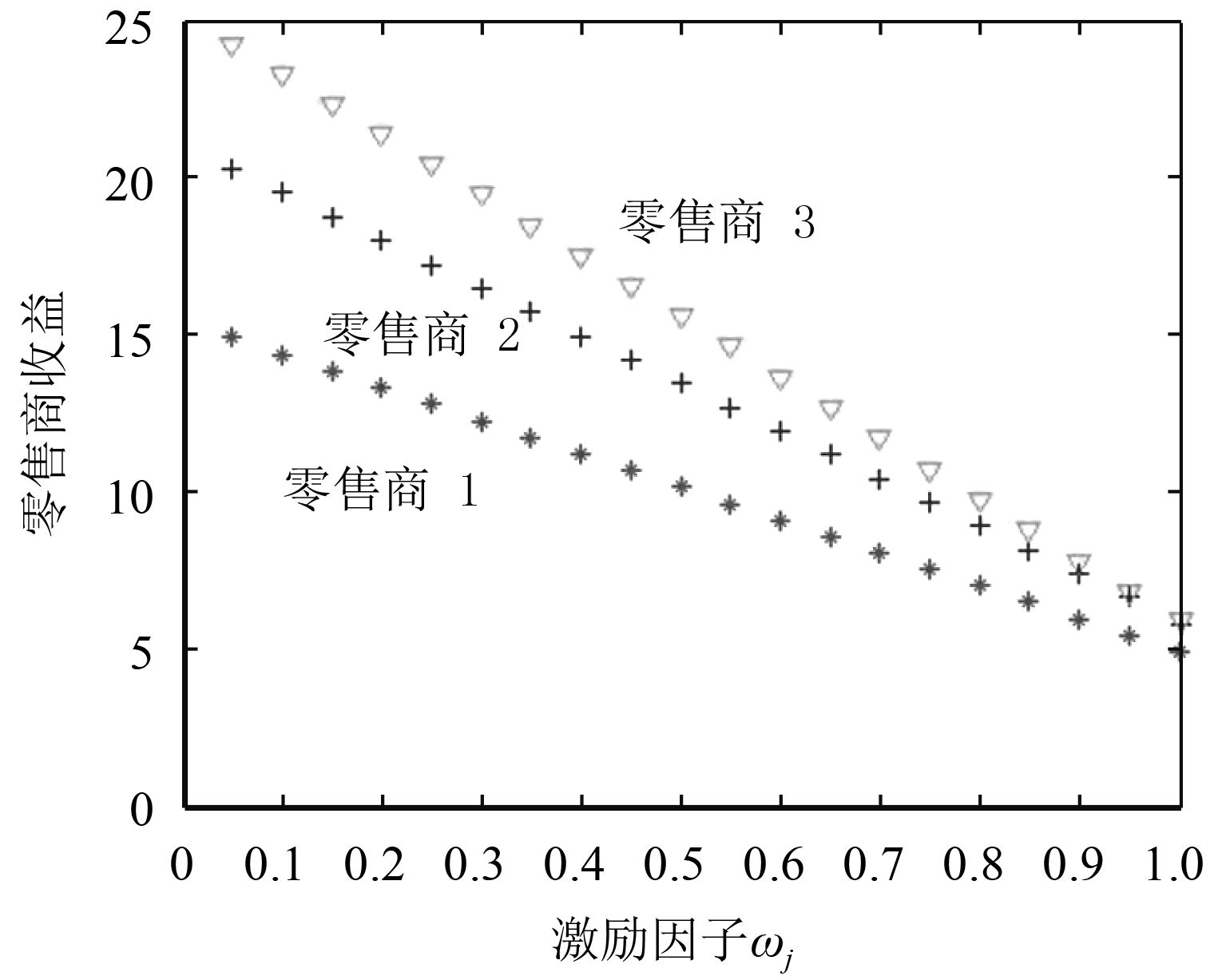
为了评价激励因子ωj 对均衡的影响,让ωj 从0.05变化到1,图6~图9说明了ωj 对用户的电力需求和效用,以及零售商的均衡价格和收入的影响。当ωj 单调递增时,每个用户的电力需求几乎保持不变。图6显示了每个用户在均衡处电力需求,但是他们的效用增加可从图8看出。这表明在ωj 作用下,用户在不增加电力需求的基础上,提高了效用。事实上,每个用户的电力需求保持稳定原因在于所有零售商的ωj 进行一致性变化让所有用户等概率选择购买零售商的电力,从而在提高用户满意度的同时,提高了用户效用,有利于用户侧积极参与需求响应中来以维持电力系统的平衡。图7和图9表明零售商的实时电价和收益变化趋势。图9描述ωj 增加时所有零售商获得的收益持续下降,图7表明ωj 增加时,零售商1降低自己的均衡价格吸引用户购买,从而获得较低收益,这一点可从图9中看出。

|
图 6 用户的实时电力需求受激励因子ωj 的影响 Fig. 6 The real-time power demand of users affected byωj |
|
图 7 零售商的实时电价受激励因子ωj 的影响 Fig. 7 The real-time power price of retailers affected byωj |
|
图 8 用户的效用受激励因子ωj 的影响 Fig. 8 The utilities of users affected byωj |
|
图 9 零售商收益受激励因子ωj 的影响 Fig. 9 The revenues of retailers affected byωj |
本文在具有多个电力零售商和多个用户的智能电网环境下,通过在电力零售商和用户之间构建Stackelberg博弈模型,来研究含激励的实时电价定价策略和最优电力消费问题,并设计一种分布式算法求解仅具有局部信息的Stackelberg均衡解。仿真结果验证了求解算法的收敛性和模型的合理性,激励因子的提出,说明了适当地给予用户一定的补贴即使对用户电力需求影响不大情形下,仍可以提高用户的满意度,有助于促使用户积极参与到需求响应中来。将来可能的研究方向包括含可再生能源相应失稳状态下以及考虑用户间仅具有局部信息时,如何发展有效的方法来进行RTP决策,新的博弈模型也是电力零售商或用户很好的选择。
| [1] |
周孝信, 鲁宗相, 刘应梅. 中国未来电网的发展模式和关键技术[J].
中国电机工程学报, 2014, 34(29): 4999-5008.
ZhOU Xiaoxin, LU Zongxiang, LIU Yingmei. Development models and key technologies of future grid in China[J]. Proceedings of the CSEE, 2014, 34(29): 4999-5008. |
| [2] | FANG X, Misra S, XUE G. Smart grid-The new and improved power grid: A survey[J]. IEEE Communications Surveys & Tutorials, 2012, 14(4): 944-980. |
| [3] | Kirschen D S. Demand side view of electricity markets[J]. IEEE Transactions on Power Systems, 2003, 18(2): 520-527. DOI: 10.1109/TPWRS.2003.810692. |
| [4] |
盛万兴, 史常凯, 孙军平. 智能用电中自动需求响应的特征及研究框架[J].
电力系统自动化, 2013, 37(23): 1-7.
SHENG Wanxing, SHI Changkai, SUN Junping. Characteristics and research framework of automated demand response in smart utilization[J]. Automation of Electric Power Systems, 2013, 37(23): 1-7. |
| [5] | Conejo A J, Morales J M, Baringo L. Real-time demand response model[J]. IEEE Transactions on Smart Grid, 2010, 1(3): 236-242. DOI: 10.1109/TSG.2010.2078843. |
| [6] | Mohsenian-Rad A H, Wong V W S, Jatskevich J. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid[J]. IEEE Transactions on Smart Grid, 2010, 1(3): 320-331. DOI: 10.1109/TSG.2010.2089069. |
| [7] | SAMADI P, MOHSENIAN-RAD A H, SCHOBER R, et al. Optimal real-time pricing algorithm based on utility maximization for smart grid[C]. 2010 First IEEE International Conference on Smart Grid Communications. Gaithersburg: IEEE, 2010: 415-420. |
| [8] | CHEN L, LI N, LOW S H, et al. Two market models for demand response in power networks[C]. 2010 First IEEE International Conference on Smart Grid Communications. Gaithersburg: IEEE, 2010: 397-402. |
| [9] | FAN Z. Distributed demand response and user adaptation in smart grids[C]. Proceedings of the 12th IFIP/IEEE International Symposium on Integrated Network Management. Dublin : IEEE, 2011: 726-729. |
| [10] | Conejo A J, Morales J M, Baringo L. Real-time demand response model[J]. IEEE Transactions on Smart Grid, 2010, 1(3): 236-242. DOI: 10.1109/TSG.2010.2078843. |
| [11] | DENG R, YANG Z, HOU F. Distributed Real-Time Demand Response in Multiseller-Multibuyer Smart Distribution Grid[J]. IEEE Transactions on Power Systems, 2015, 30(5): 2364-2374. DOI: 10.1109/TPWRS.2014.2359457. |
| [12] | Crew M A, Fernando C S, Kleindorfer P R. The theory of peak-load pricing: a survey[J]. Journal of regulatory economics, 1995, 8(3): 215-248. DOI: 10.1007/BF01070807. |
| [13] | ZENG S, LI J, REN Y. Research of time-of-use electricity pricing models in China: A survey[C]. IEEE International Conference on Industrial Engineering and Engineering Management. Singapore: IEEE, 2008: 2191-2195. |
| [14] |
代业明, 高岩. 基于智能电网需求侧管理的多零售商实时定价策略[J].
中国电机工程学报, 2014, 34(22): 3575-3589.
DAI Yeming, GAO Yan. Real-time pricing strategy with multi-retailers based on demand-side management for the smart grid[J]. Proceedings of the CSEE, 2014, 34(22): 3575-3589. |
| [15] | Borenstein S, Jaske M, Rosenfeld A. Dynamic pricing, advanced metering, and demand response in electricity markets[J]. Journal of the American Chemical Society, 2002, 128(12): 4136-4145. |
| [16] | Paschalidis I C, Li B, Caramanis M C. Demand-side management for regulation service provisioning through internal pricing[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1531-1539. DOI: 10.1109/TPWRS.2012.2183007. |
| [17] | IBARS C, NAVARRO M, GIUPPONI L. Distributed demand management in smart grid with a congestion game[C]. 2010 First IEEE International Conference on Smart Grid Communications. Gaithersburg: IEEE, 2010: 495-500. |
| [18] | DAI Yeming, GAO Yan. Real-Time Pricing Decision Based on Leader-Follower Game in Smart Grid[J]. Journal of Systems Science and Information, 2015, 3(4): 348-356. |
| [19] |
代业明, 高岩. 具有多类资源多类用户智能电网实时定价决策[J].
系统工程理论与实践, 2015, 35(9): 2315-2323.
DAI Yeming, GAO Yan. Real-time pricing decision making in smart grid with multi-type users and multi-type power sources[J]. Systems Engineering-Theory and Practice, 2015, 35(9): 2315-2323. |
| [20] | Chai B, Chen J, Yang Z. Demand response management with multiple utility companies: A two-level game approach[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 722-731. DOI: 10.1109/TSG.2013.2295024. |
| [21] | Kamyab F, Amini M, Sheykhha S. Demand response program in smart grid using supply function bidding mechanism[J]. IEEE Transactions on Smart Grid, 2015, 7(3): 1277-1284. |
| [22] | Maharjan S, Zhu Q, Zhang Y. Dependable demand response management in the smart grid: A Stackelberg game approach[J]. IEEE Transactions on Smart Grid, 2013, 4(1): 120-132. DOI: 10.1109/TSG.2012.2223766. |
| [23] | BASAR T, OLSDER G J. Dynamic non-cooperative game theory[M]. ser. SIAM Series in Classics in Applied mathematics. Philadelphia, PA: SIAM, 1999. |
 2017, Vol. 20
2017, Vol. 20