2. 湖北理工学院 经济与管理学院 湖北 黄石 435001
2. Economics and Management School, Hubei Polytechnic University, Huangshi 435001, China
随着我国经济的快速发展,城镇化的发展也愈发迅速,使得城市人口的数量剧增,进而导致生活垃圾的大量排放。我国城市生活垃圾的年产量已经达到1.78×108 t,近年来以年均3%左右的速度增长。因此,如何处理好伴随城镇化而产生的生活垃圾,是能否“全面建成小康社会”的一个关键。
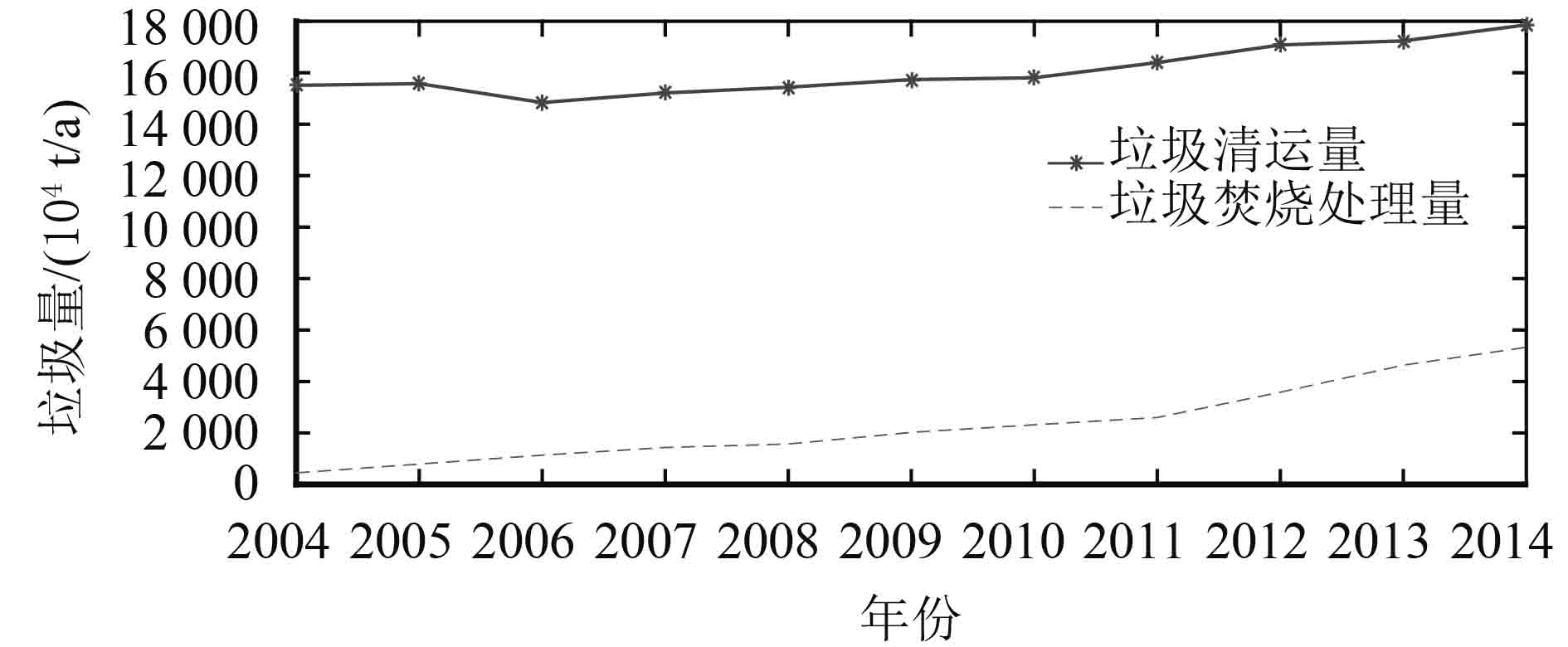
目前,我国处置生活垃圾的方法主要集中在卫生填埋、垃圾焚烧发电以及其他方式。其中垃圾焚烧发电呈现出稳定增长的趋势,逐渐成为我国处理垃圾的主要方式(如图1,数据根据中国统计年鉴2004-2015整理[1])。垃圾发电,是指利用特殊的垃圾焚烧设备,以城市工业和生活垃圾作为燃烧介质,然后用其散发出的能量发电的一种新型发电方式。利用焚烧垃圾余热发电,有别于一般的火力发电和核能发电,它利用城市废弃物替代正在日益减少的煤、石油等天然燃料,具有绿色环保意义,符合可持续发展战略,是国家积极鼓励的新能源发电方式之一[2]。根据国家相关规划,全国生活垃圾焚烧能力2020年将超过4×105 t/d,2025年可达5×105 t/d[3]。
|
图 1 我国城市生活垃圾清运量及垃圾焚烧处理量趋势 Fig. 1 MSW disposal and incineration capacity trends in China |
“十三五”规划对于垃圾处理,提出了垃圾治理无害化、资源化、减量化和社会化的理念[4]。对于垃圾焚烧发电行业而言,在焚烧发电过程中所产生的残留物(主要为炉渣、飞灰)对环境的污染一直都是社会公众所关注的焦点。从2016年1月1日起,全国所有新建、已运行的生活垃圾焚烧炉必须执行新《生活垃圾焚烧污染控制标准》(GB18485-2014)的污染物排放限值。新标准对常规污染物、二恶英类污染物都有更为严格的规定[4]。那么如何促使垃圾焚烧发电企业能够主动对于焚烧残留物实行无害化处理,严格遵守新标准,这也成为城市生活垃圾管理中亟待解决的问题。
1 文献综述垃圾焚烧发电在生产运营过程中,对周边环境以及居民的影响,引起了诸多学者的关注。Petts[5]通过分析垃圾焚烧对英国公众带来的影响,从选址、风险的可接受性等方面进行了分析,提出加强沟通与教育的对策。但如果在运营过程中进行妥善处理,垃圾焚烧发电不仅不会对环境有太多影响,还会有助于循环经济的发展。Antoine等[6]运用生命周期方法比较了法国110座垃圾焚烧发电厂的环境影响,发现采取不同处理技术的垃圾焚烧发电厂,对周边环境的影响也不同。Yuliya等[7]通过研究表明如果在垃圾焚烧过程中,采取合适的处理方式,那么垃圾焚烧残留物不再是一种环境污染物,而是一种资源。国外一些学者还发现垃圾焚烧残留物如果经过恰当处理,可以提供一些可供回收的矿产及金属资源[8,9]。Bozorgira[10]提出垃圾焚烧是否无害化依赖于政府的政策。Nixon[11]提出垃圾无害化处理的关键在于选择合适的技术、处理能力。俞祖成等[12]以利益主体为博弈参与者,通过静态博弈的方法得出政府、垃圾焚烧发电企业、公众最终的纳什均衡为{合作,合作,抵抗}的决策结果。刘承毅等[13]从声誉激励的角度构建纳入举报机制的由社会民众、政府规制机构和特许经营企业三方参与的序列博弈模型提出社会监督的重要性。李郁芳等[14]通过建立和分析垃圾焚烧发电项目力量悬殊的最后通牒博弈模型,得出由于政府职能错位导致牺牲业主利益的结论。
进化博弈论最早由Smith和Price[15]在研究对称人口博弈时提出,它是将博弈论和动态进化过程结合起来的一种新理论,并提出了进化稳定策略(evolutionarily stable strategy, ESS)。在传统的博弈论中,通常假设博弈参与者都是理性人和对称信息,而Selten[16]提出进化博弈则是认为博弈参与者是有限理性,并且信息是非对称的。Hirshleifer[17]提出了进化均衡(evolutionary equilibrium, EE)的概念。他提出,如果从动态系统中的某个平衡点的任意一个小领域处罚的轨迹都最终进化趋向于给均衡点,则该均衡点是渐进稳定的,这个动态稳定均衡点就是进化均衡。关于进化均衡Friedman[18]得出了3点结论:1)每一个纳什均衡都是动态系统的均衡点;2)进化均衡一定是纳什均衡;3)进化稳定策略不一定是进化均衡,而复制动态方程可以保证进化稳定策略是进化均衡。Taylor和Jonker[19]认为复制动态方程是在进化博弈理论中运用最普遍的选择机制动态方程。国内也有一些学者对进化博弈有所研究,并运用其对一些问题进行分析。孙庆文等[20]对非对称的重复博弈的进化稳定性进行了分析。邱中华等[21]基于进化博弈来分析一种监查博弈模型。蔡玲如等[22]将进化博弈同系统动力学相结合,对环境污染问题中的非对称进化博弈做了均衡稳定性分析。达庆利等[23]分析了两个博弈参与方的3×3对称进化博弈的稳定状态。魏芳芳等[24]建立了三个博弈参与者的非对称进化博弈模型,并讨论了三方各自的均衡点以及渐近稳定条件。刘连光等[25]依据收益矩阵建立风火网三方2×2×2非对称进化博弈复制动态系统,并分析了各个平衡点的渐进稳定性条件。特日昆等[26]运用进化博弈模型来分析银政企三方非合作的信贷融资问题。朱庆华[27]运用进化博弈模型政企双方就绿色供应链问题进行了研究。
上述文献主要集中于静态或双方进化博弈,鲜有涉及动态或三方博弈模型。因而,本文通过构建中央政府、地方政府、垃圾焚烧发电企业三方进化博弈模型,并通过系统动力学来研究博弈模型的进化稳定策略。针对初始模型不存在进化稳定策略的情况,提出动态惩罚策略和动态奖励策略来寻找控制策略波动的方案。最后通过敏感性分析来寻找实现理想的策略组合方案条件。
2 垃圾发电绿色生产进化博弈模型 2.1 问题描述目前我国城市生活垃圾处理,逐渐从原来的填埋、堆肥向可循环处理方式转变,其中以焚烧发电为主。但是由于对垃圾焚烧发电企业的监督管理制度不够完善,使得垃圾焚烧发电企业为了自身利益,在垃圾处理过程中未采用绿色处置方式,对周边环境产生二次污染。这也使得近年来,居民对于垃圾焚烧发电行业敬而远之,出现邻避效应。怎样促使垃圾焚烧发电企业在垃圾处理过程中实行绿色生产,真正实现垃圾循环发展。这是一个值得探讨的问题。
进化博弈论通常假设参与者是有限理性,并且是动态博弈,它将博弈论和动态进化过程分析融合在一起。进化博弈不同于传统博弈,当被多个竞争策略影响时,它更注重策略改变的动态性。
在垃圾焚烧发电绿色生产中,垃圾焚烧发电企业都是有限理性的,并且他们会通过观察比较其他企业的收益来改变调整自身的策略。因此,进化博弈可以用来分析如何促进我国垃圾焚烧企业实行垃圾焚烧发电绿色生产的长期过程。
目前,“十三五”规划提出了垃圾无害化、资源化的处理目标。这需要中央政府给予政策支持,地方政府对垃圾焚烧企业进行监管控制,垃圾焚烧发电企业来执行。本文将通过进化博弈对这三方策略选择进行研究。
2.2 模型假设做如下假设。
1)假设博弈参与方为中央政府、地方政府和垃圾焚烧发电企业三方,且均为经济人。
2)对于中央政府来说,为了促进垃圾无害化、资源化治理,会给予垃圾发电企业一定的优惠政策,中央政府可以通过检查来了解企业对政策目标的执行情况。令中央政府检查的几率为X(0≤X≤1)。中央政府实行检查需要耗费人力、物力、财力,因而存在成本CG,并且由于中央政府在检查时,对于企业的了解程度不如地方政府,因而其检查成本会高于地方监管成本。当中央政府不检查时,如果垃圾发电企业未采用绿色生产,则会对环境和居民造成伤害,使得社会福利损失为WG,当中央政府检查时,如果垃圾发电企业未采用绿色生产,则对其进行处罚PE,如果企业采用了绿色生产,则政府对其进行奖励BE。如果检查发现地方政府未履行监管职责,则对其进行处罚PL,如果履行了监管职能,则进行奖励BL。
3)假定垃圾发电企业采用绿色生产的几率为Z(0≤Z≤1)。垃圾发电企业进行生产可以获得垃圾处理补贴以及上网电价补贴,令其收益为πE。垃圾发电企业在处理垃圾过程中采用绿色生产时,其绿色生产设备投资为CE。如果企业不采用绿色生产,可以选择对地方政府进行贿赂WB[28],使得地方政府的监管采取渎职的方式。令CB、CNB分别表示对地方政府贿赂和不贿赂时企业的总成本。
4)假设地方政府进行监管的几率为Y(0≤Y≤1)。当地方政府对垃圾发电企业实行严格监督时,令其监管成本为CL,由于垃圾发电企业为地方政府解决垃圾围城及地方就业等问题,则地方政府可以获得收益πL。如果地方政府接受企业贿赂,则对企业监督实行渎职,由于垃圾焚烧企业未采用绿色生产对周边环境造成二次污染,社会福利造成的损失为WL。
|
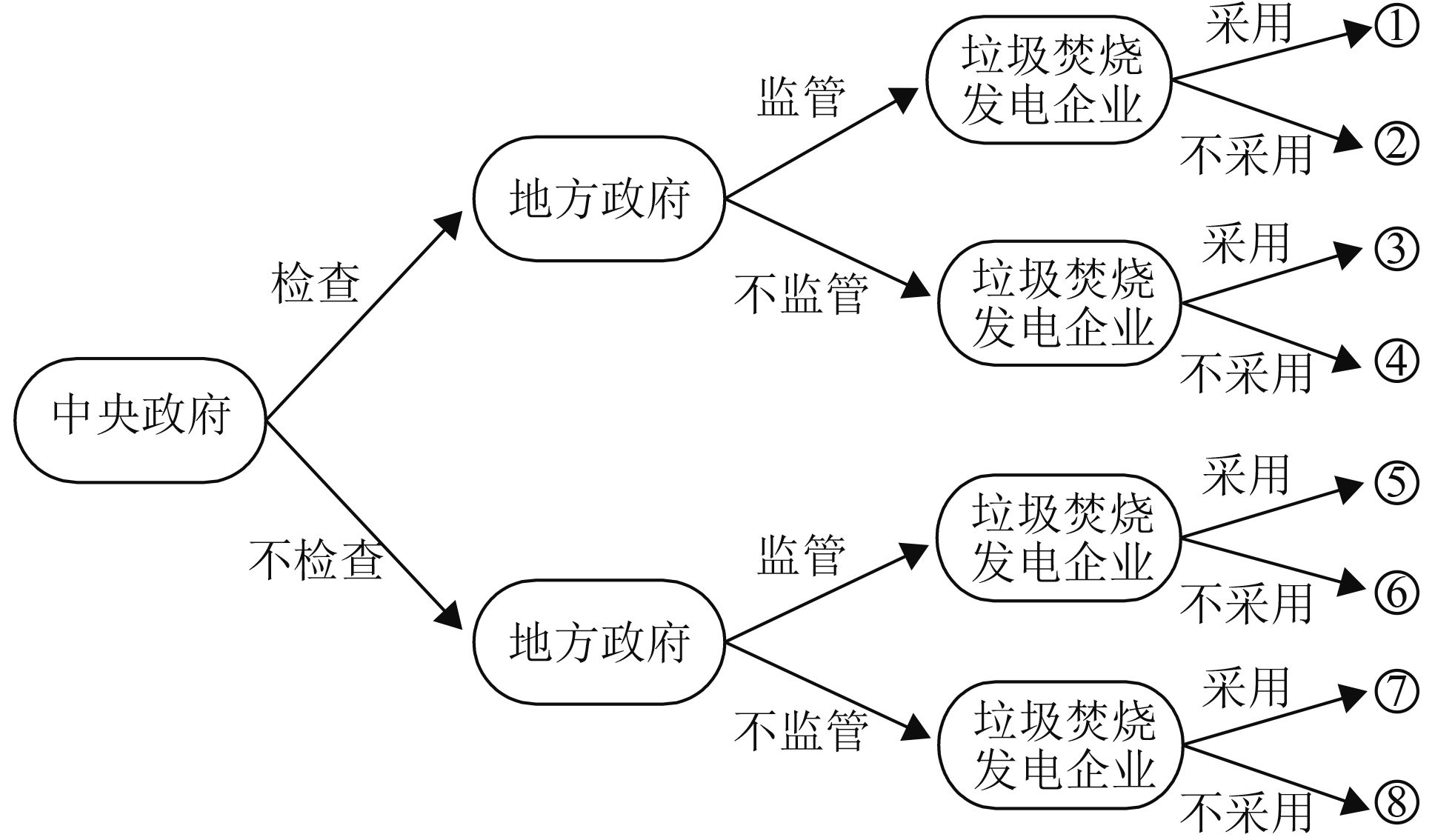
图 2 垃圾绿色生产的三方博弈树 Fig. 2 Three players game tree under waste harmless disposal |
| 表 1 三方收益矩阵 Tab. 1 Payoff matrix among three players |
根据博弈树的收益,设中央政府检查的收益为U1Y,不检查的收益为U1N,平均收益为U1,则
| $\begin{array}{l}\quad\ \ {U_{1{\rm{Y}}}} = YZ( \!-\! {C_{\rm{G}}} \!-\! {B_{\rm{E}}} \!-\! {B_{\rm{L}}}) + Y(1 \!-\! Z)( \!-\! {C_{\rm{G}}} \!-\! {B_{\rm{L}}} + {P_{\rm{E}}}) + \\[5pt]\!\!\!\! (1 - Y)Z( - {C_{\rm{G}}} + {P_{\rm{L}}} - {B_{\rm{E}}}) + (1 - Y)(1 - Z)( - {C_{\rm{G}}} + {P_{\rm{E}}} + {P_{\rm{L}}}){ \text{,}}\end{array}$ | (1) |
| $\begin{split}& \quad\quad {U_{1{ \rm N}}} = YZ \times 0 + (1 - Y)Z( - {W_{\rm G}}) + Y(1 - Z) \times 0 + \\& (1 - Y)(1 - Z)( - {W_{\rm G}}) \text{,}\end{split}$ | (2) |
| $\quad\quad {U_1} = X \times {U_{1{ \rm Y}}} + (1 - X){U_{1{ \rm N}}} \text{。}$ | (3) |
由式(1)~(3)可得中央政府的复制动态方程为
| $\begin{split}& \quad\quad \ F(X) = \frac{{{\rm{d}}X}}{{{\rm{d}}t}} = X({U_{1{\rm Y}}} - {U_1}) = \\& X(1 - X)({U_{1{\rm Y}}} - {U_{1{\rm N}}}) = X(1 - X)[ - Y({B_{\rm{L}}} + {P_{\rm{L}}} + {W_{\rm{G}}}) - \\& Z({B_{\rm{E}}} + {P_{\rm{E}}}) + {P_{\rm{E}}} + {P_{\rm{L}}} + {W_{\rm{G}}} - {C_{\rm{G}}}]\text{。}\end{split}$ | (4) |
设地方政府监管的收益为U2Y,不监管的收益为U2N,平均收益为U2,则
| $\begin{split}& \quad\quad {U_{2{\rm Y}}} \!=\! XZ({\pi _{\rm{L}}} \!+\! {B_{\rm{L}}} \!-\! {C_{\rm{L}}}) + X(1 \!-\!Z)({\pi _{\rm{L}}} + {B_{\rm{L}}} \!-\! {C_{\rm{L}}}) + \\ & (1 - X)Z({\pi _{\rm{L}}} - {C_{\rm{L}}}) + (1 - X)(1 - Z)({\pi _{\rm{L}}} - {C_{\rm{L}}}){{\text{,}}}\end{split}$ | (5) |
| $\begin{split}& \quad\quad {U_{2{\rm N}}} \!=\! XZ({\pi _{\rm{L}}} \!-\! {P_{\rm{L}}}) \!+\! X(1 \!-\! Z)({\pi _{\rm{L}}} \!+\! {W_{\rm{B}}} \!-\! {P_{\rm{L}}} \!-\! {W_{\rm{L}}}) + \\& (1 - X)Z({\pi _{\rm{L}}}) + (1 - X)(1 - Z)({\pi _{\rm{L}}} + {W_{\rm{B}}} - {W_{\rm{L}}}){\text{,}}\end{split}$ | (6) |
| $\quad\quad {U_2} = Y {U_{2{{ \rm Y}}}} + (1 - Y){U_{2{\rm N}}} \text{。}$ | (7) |
地方政府的复制动态方程为
| $F(Y) = \frac{{{\rm d}Y}}{{{\rm d}t}} = Y(1 - Y) \times[(1 \!-\! Z)({W_{\rm L}} \!-\! {W_{\rm B}}) \!+\! X({B_{\rm L}} \!+\! {P_{\rm L}}) \!-\! {C_{\rm L}}] \text{。}$ | (8) |
设垃圾发电企业采用绿色生产的收益为U3Y,不采用绿色生产的收益为U3N,平均收益为U3,则
| $\begin{split}& \quad\quad {U_{3{\rm Y}}} \!=\! XY({\pi _{\rm{E}}} \!+\! {B_{\rm{E}}} \!-\! {C_{\rm{E}}}) \!+\! X(1 \!-\! Y)({\pi _{\rm{E}}} \!+\! {B_{\rm{E}}} \!-\! {C_{\rm{E}}}) +\! \\ & (1 - X)Y({\pi _{\rm{E}}} - {C_{\rm{E}}}) + (1 - X)(1 - Y)({\pi _{\rm{E}}} - {C_{\rm{E}}}){\text{,}}\end{split}$ | (9) |
| $\begin{split}& \quad\quad {U_{3{\rm N}}} \!=\! XY({\pi _{\rm{E}}} \!-\! {P_{\rm{E}}} \!-\! {C_{{\rm{NB}}}}) \!+\! X(1 \!-\! Y)({\pi _{\rm{E}}} \!-\! {P_{\rm{E}}} \!-\! {C_{\rm{B}}}) +\! \\& (1 - X)Y({\pi _{\rm{E}}} - {C_{{\rm{NB}}}}) + (1 - X)(1 - Y)({\pi _{\rm{E}}} - {C_{\rm{B}}}){\text{,}}\end{split}$ | (10) |
| $\quad\quad{U_3} = Z {U_{3{\rm Y}}} + (1 - Z){U_{3{\rm N}}} \text{。}$ | (11) |
垃圾发电企业的复制动态方程为
| $\begin{split}& \quad\quad F(Z) = \frac{{{\rm d}Z}}{{{\rm d}t}} = Z(1 - Z)[X({B_{\rm E}} + {P_{\rm E}}) + \\ & Y({C_{\rm NB}} - {C_{\rm B}})+{C_{\rm B}} - {C_{\rm E}}] \text{。}\end{split}$ | (12) |
联立式(4)、(8)、(12),可得动态系统的复制动态方程组
| $ \quad \quad \left\{{\begin{aligned}& F(X) = \frac{{{\rm d}X}}{{{\rm d}t}} = X({U_{1{ Y}}} - {U_1}) = \\& \quad \quad X(\!1 \!-\! X\!)(\!{U_{1{ Y}}} \!-\! {U_{1{ N}}}\!) \!=\! X(\!1 \!-\! X) [ - Y(\!{B_{\rm L}} \!+\! {P_{\rm L}} \!+\! {W_{\rm G}}\!) - \\ & \quad \quad Z({B_{\rm E}} + {P_{\rm E}}) + {P_{\rm E}} + {P_{\rm L}} + {W_{\rm G}} - {C_{\rm G}}] \text{,}\\& F(Y) = \frac{{{\rm d}Y}}{{{\rm d}t}} = Y(1 - Y) [(1 - Z)({W_{\rm L}} - {W_{\rm B}}) + \\ & \quad \quad X({B_{\rm L}} + {P_{\rm L}}) - {C_{\rm L}}] \text{,}\\& F(Z) = \frac{{{\rm d}Z}}{{{\rm d}t}} = Z(1 - Z)[X({B_{\rm E}} + {P_{\rm E}}) +\\& \quad \quad Y({C_{\rm NB}} - {C_{\rm B}}) + {C_{\rm B}} - {C_{\rm E}}] \text{。}\end{aligned}} \right.$ | (13) |
由式(13)可得博弈模型的雅克布矩阵
| $\begin{array}{*{20}{c}}{J \!\!= } & {\left[ {\begin{array}{*{20}{c}} {(1 - 2X)C(Y,Z)} & {X(1 - X)\displaystyle\frac{{\text{∂}l C(Y,Z)}}{{\text{∂} Y}}} & {X(1 - X)\displaystyle\frac{{\text{∂} C(Y,Z)}}{{\text{∂} Z}}}\\[8pt] {Y(1 - Y)\displaystyle\frac{{\text{∂} L(X,Z)}}{{\text{∂} X}}} & {(1 - 2Y)L(X,Z)} & {Y(1 - Y)\displaystyle\frac{{\text{∂} L(X,Z)}}{{\text{∂} Z}}}\\[8pt] {Z(1 - Z)\displaystyle\frac{{\text{∂} E(X,Y)}}{{\text{∂} X}}} & {Z(1 - Z)\displaystyle\frac{{\text{∂} E(X,Y)}}{{\text{∂} Y}}} & {(1 - 2Z)E(X,Y)}\end{array}} \right]}{\text{。}}\end{array}$ | (14) |
其中,
由于模型均衡点求解较为复杂,为了便于分析,本文将相关指标进行赋值来求解各个均衡点,并通过系统动力学的方法来分析博弈模型各个均衡点的稳定性,模型中参数的初始赋值如表2所示。表2中各参数赋值应满足以下条件。
| 表 2 系统动力博弈模型指标赋值 Tab. 2 The values of variables in the SD game model |
1)地方政府比中央政府更了解企业生产状况,因此中央政府的检查成本要比地方政府的高。
2)当垃圾发电企业为采用绿色生产,对社会环境、居民健康造成损害时,由于污染存在流动性,除了对当地造成污染外,还可能对周边区域造成污染。因此,中央政府则要花更多的时间、精力和金钱来弥补整个社会的损失,所以中央政府的福利损失要比地方政府的福利损失更大。
3)在垃圾发电企业项目刚刚实施时,对当地环境及居民的危害还并不明显,因而对未采用绿色生产企业以及对未履行监管职责的地方政府的初始罚款不会很高。并且如果对周边环境及居民产生的危害,企业为第一责任人,因而对企业的罚款要更高。
4)对于企业和地方政府分别履行其职责的奖励也依据责任关系进行区分,因而企业的奖励标准要高于地方政府的标准,假定初始奖励标准为惩罚标准的一半。
5)企业的收益会有一部分溢出到地方经济中,因而其收益高于地方政府收益,假定企业收益为地方政府收益的2倍。
6)假定企业进行绿色生产的投资成本为企业收益的一半。
7)当企业贿赂地方政府时,其会获得一部分收益用于抵消其总成本,因而贿赂时的总成本必然小于不进行贿赂的总成本与贿赂金额之和。
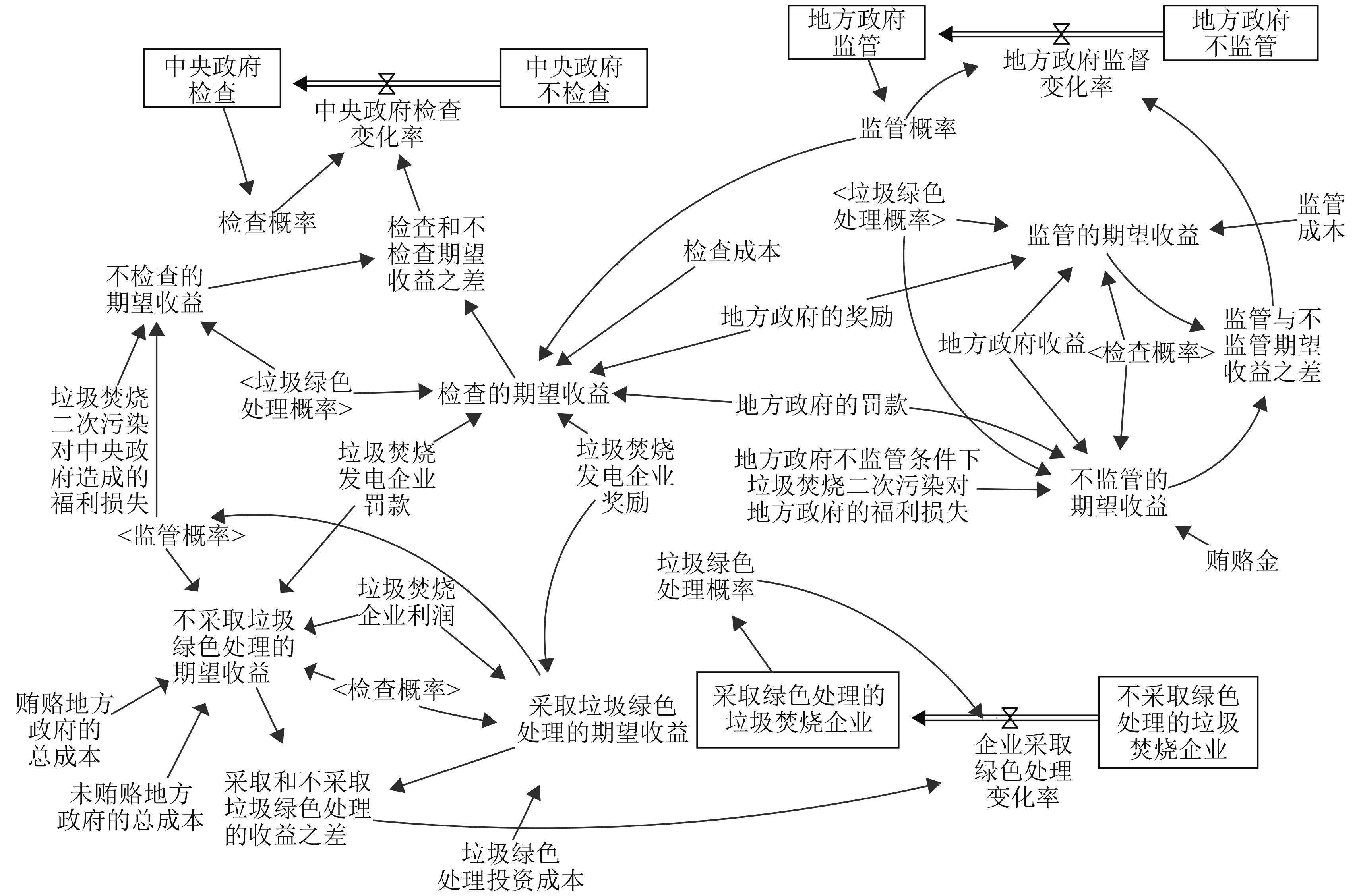
3 基于系统动力学的进化博弈稳定性分析在进化博弈中,每个博弈方都通过观察和比较其他博弈方的收益,向其他博弈方学习和模仿,并调整他们的策略,是一种动态博弈。因此,有些学者运用系统动力学的方法来分析均衡解的稳定性[30]。因此,运用系统动力学来求解ESS是可行的。根据上述的博弈模型假设,运用软件Vensim DSS 5.6a,建立系统动力学进化博弈模型如图3所示。该模型由3个子系统构成,分别为中央政府子系统、地方政府子系统以及垃圾焚烧发电企业子系统。模型中的所有变量间的关系参照3个复制动态方程。
|
图 3 三方进化博弈系统动力学模型 Fig. 3 The evolutionary game system dynamics model among 3 parties |
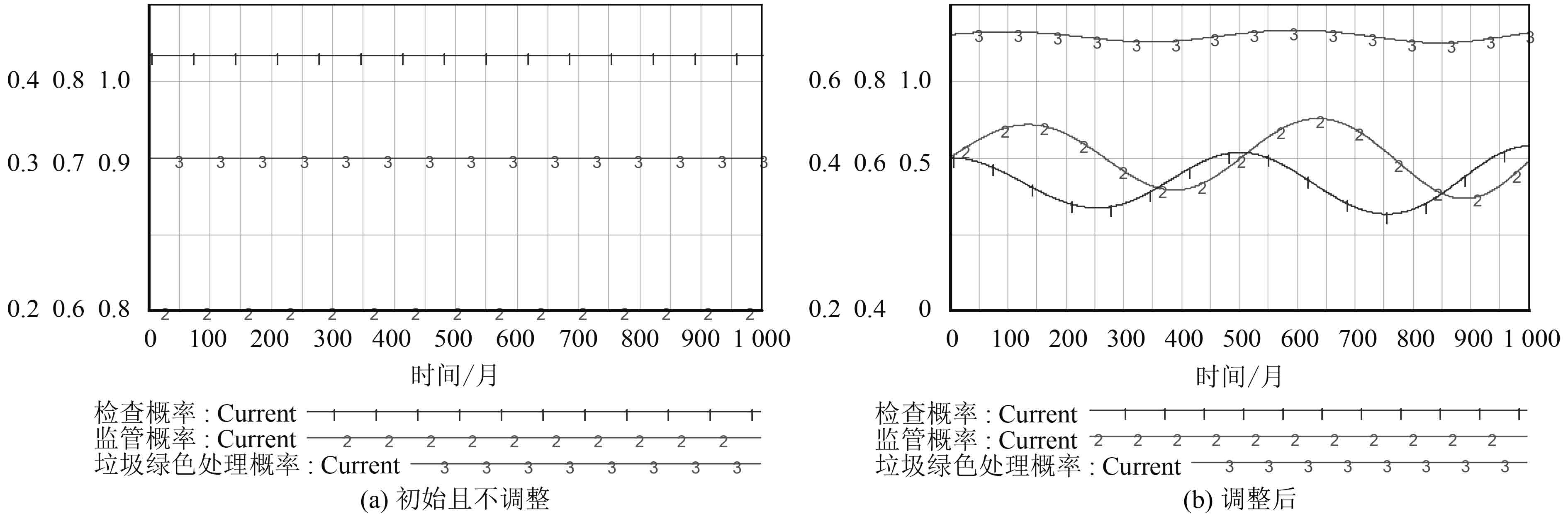
将赋值代入方程组(13),求得存在11个符合X,Y,Z∈[0, 1]的均衡解,其中8个纯策略,3个混合策略:E1=(0, 0, 0),E2=(0, 0, 1),E3=(0, 1, 0),E4=(0, 1, 1),E5=(1, 0, 0),E6=(1, 1, 0),E7=(1, 0, 1),E8=(1, 1, 1),E9=(0.5, 1, 0.17),E10=(0.33, 0.55, 1),E11=(0.37, 0.6, 0.9)。以E11为例,运用Vensim DSS 5.6a进行仿真,模型设定如下:INITIAL TIME=0,FINAL TIME=1000,TIME STEP=1,Units for Time=Month。仿真结果如图4所示。
|
图 4 均衡点E11初始及调整后的仿真模拟结果 Fig. 4 The simulation results under initial and adjusting strategy of equilibrium E11 |
由图4(a)可知,博弈三方不会改变他们的初始策略,表现出相对稳定的状态。如果稍微改变其初始选择策略(如将检查概率X由0.37改为0.4),则仿真结果如图4(b),均衡点E11的平衡状态并不稳定。仅仅对中央政府初始选择进行一点微小的变化,便会使得博弈三方的选择呈现波动状态,其博弈进化趋势如图5所示。因而,该博弈模型不存在均衡稳定策略。
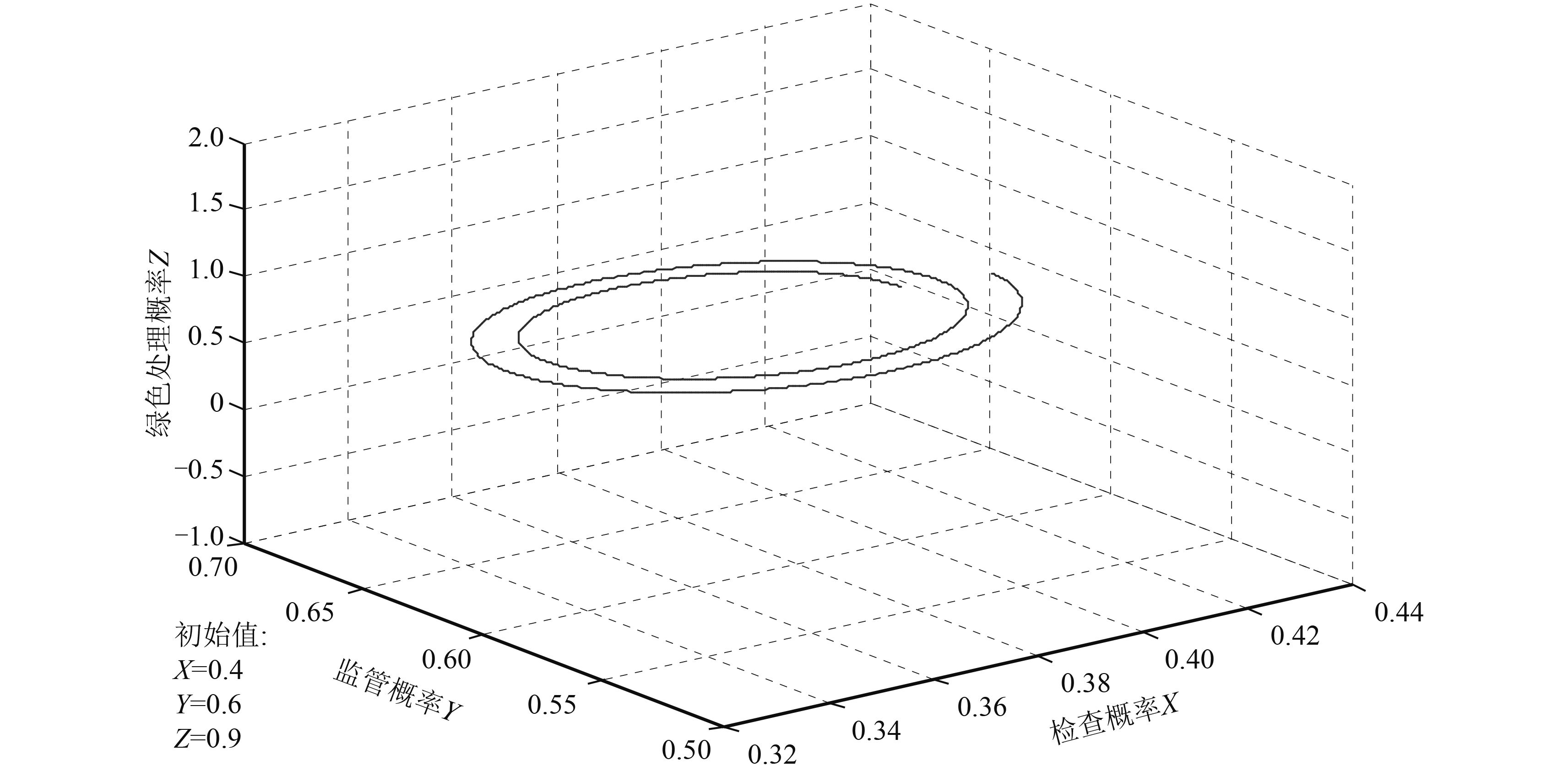
|
图 5 博弈三方混合策略博弈进化过程 Fig. 5 Mixed-strategy game evolutional process among 3 parties |
根据李雅普诺夫稳定性理论,可以通过分析雅克比矩阵的特征值的方法来分析系统在均衡点上的稳定性特征。若所有特征值均具有非正实部(至少有一个为0),则系统稳定;若所有特征值均具有负实部,则系统渐进稳定;若至少有一个特征值具有正实部,则系统不稳定。由表3可知,该模型不存在均衡稳定策略(ESS)。该结论同仿真结果相同。
| 表 3 模型中各均衡点及其特征值 Tab. 3 Equilibrium point and characteristic values of the SD game model |
在进化博弈模型不存在均衡稳定策略的情况下,可以通过引入政府的动态奖励策略来控制模型的策略波动[31]。由于垃圾焚烧企业是需要依赖政府补贴才能盈利的行业,其奖励应同采取绿色处理概率成正比。假定地方政府和企业的动态奖励策略分别为BL′=YBL和BE′=ZBE。
4.1 仿真分析在动态奖励的情况下,将初始策略A(X=0.5,Y=0.5,Z=0.5)代入模型进行仿真分析,结果如图6所示,其博弈进化趋势如图7所示。综上所述,在动态奖励策略条件下,对于垃圾焚烧发电行业,不存在进化稳定策略。
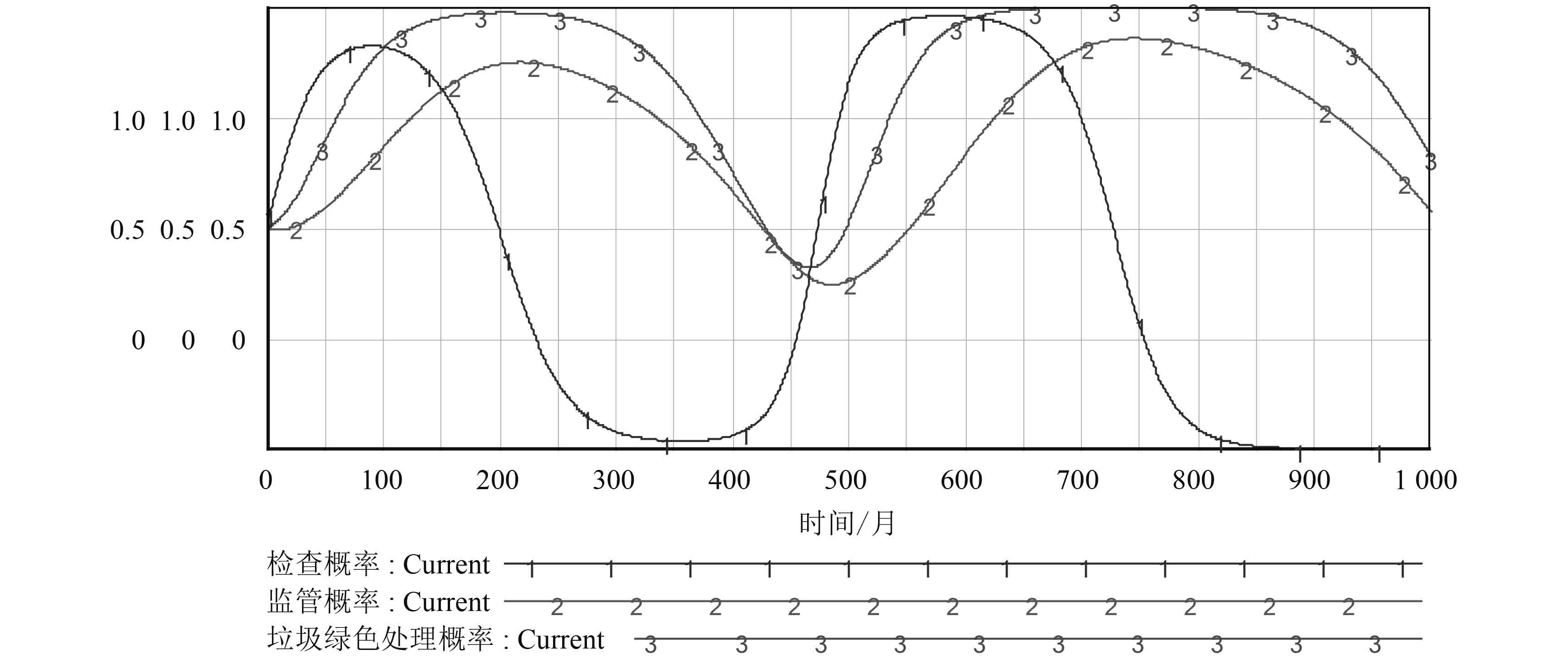
|
图 6 动态奖励策略的仿真模拟 Fig. 6 The simulation results under dynamic reward strategy |
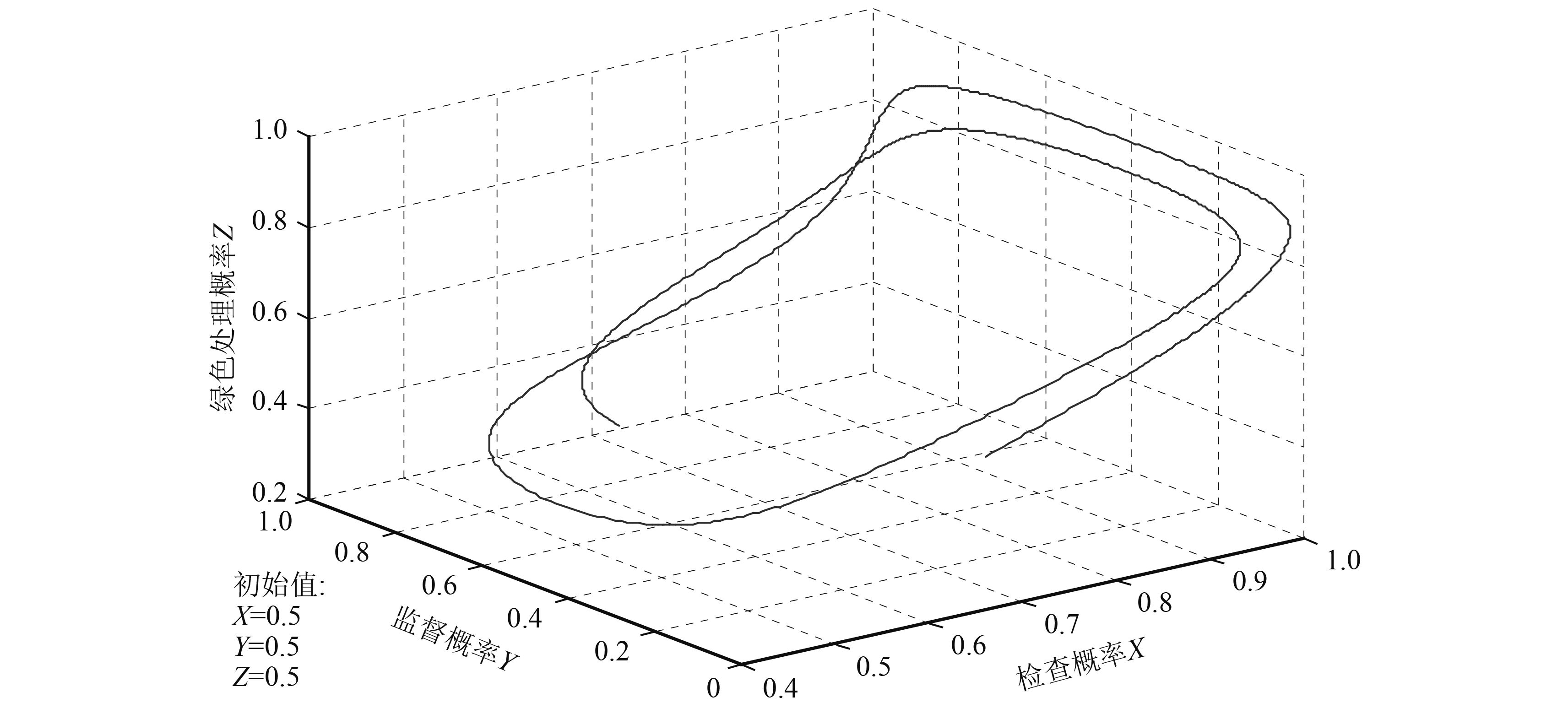
|
图 7 动态奖励策略下博弈3方混合策略博弈进化过程 Fig. 7 Mixed-strategy game evolutional process among 3 parties under dynamic reward strategy |
将BL′=YB
求各个均衡解的特征值,无一满足李雅普诺夫稳定性理论中的渐进稳定条件。因此引入动态奖励策略,对于垃圾焚烧发电企业而言,无法避免博弈策略的波动,不存在博弈均衡稳定策略。
5 动态惩罚策略在控制策略波动的研究中,有些学者提出可以通过实行动态惩罚策略来控制模型的策略波动问题[22,30-31]。假设中央政府根据垃圾焚烧企业是否采取绿色处理以及地方政府是否进行监管,对二者实行动态罚款。则地方政府和企业的罚款分别为PL′=(1-Y)PL和PE′=(1-Z)PE,PL和PE分别表示罚款的最高标准。
5.1 仿真分析在动态罚款的情况下,分别将初始策略A(X=0.5,Y=0.5,Z=0.5)及策略B(X=0.1,Y=0.2,Z=0.1)代入模型进行仿真分析,结果如图8(a)、8(b)所示。
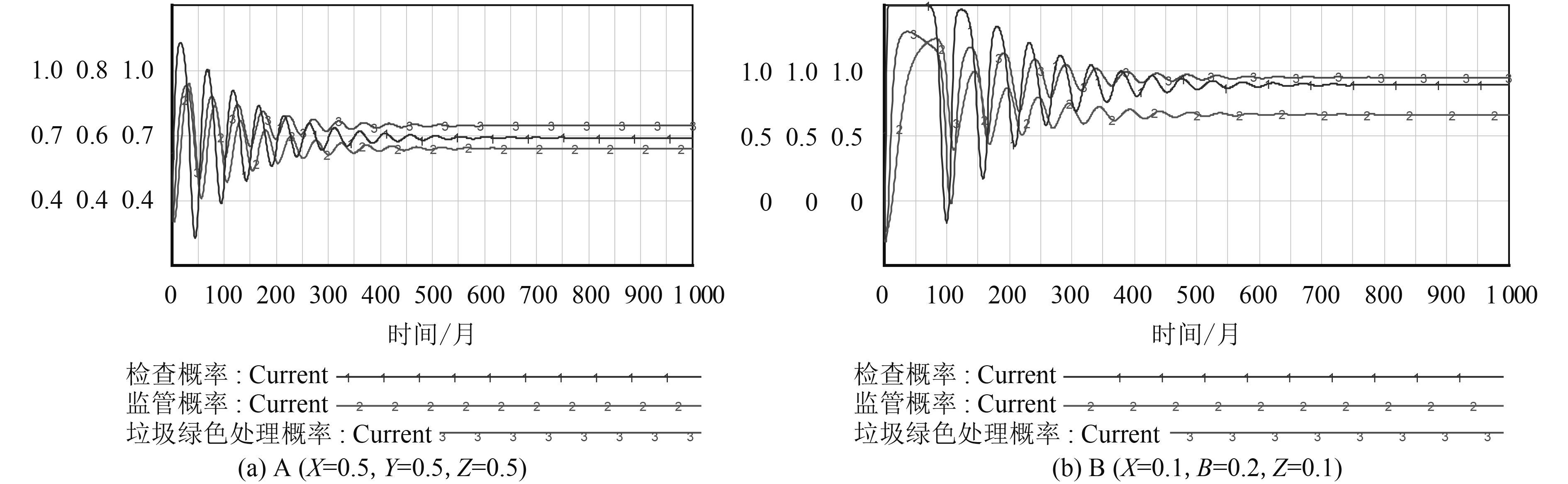
|
图 8 不同初始策略的仿真模拟结果 Fig. 8 The simulation results under different initial strategy |
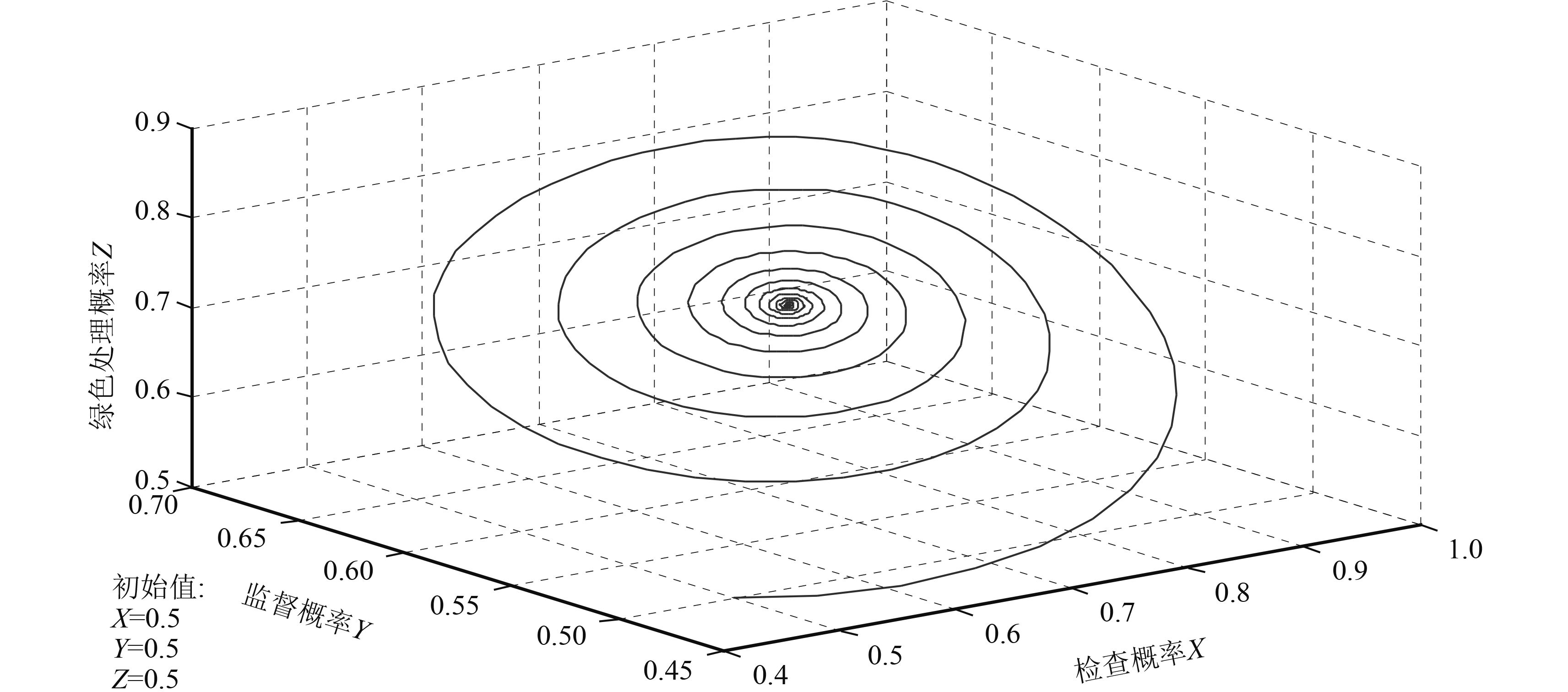
模拟结果表明,引入动态惩罚机制后,存在ESS,使得模型处于渐进稳定状态。其渐进稳定过程如图9所示。
|
图 9 动态惩罚策略下博弈三方混合策略博弈进化过程 Fig. 9 Mixed-strategy game evolutional process among 3 parties under dynamic penalty strategy |
由于采取动态惩罚策略,因此原博弈模型将发生改变。将PL ′=(1-Y)PL,PE′=(1-Z)PE代入式(13)中,求得其均衡点为8个纯策略解和6个符合X,Y,Z∈[0, 1]的混合策略解,分别为E9′=(1, 0.5, 0),E10′=(1, 1, 0.75),E11′=(0.5, 0.5, 1),E12′=(1, 0.9, 0.8),E13′=(0.54, 1, 0.1),E14′=(0.69, 0.58, 0.72)。
分别求14个均衡解的特征值,发现E1′~E13′的特征值都无法满足李雅普诺夫稳定性理论中的渐进稳定条件,而E14′的特征值为λ1=-0.557 2,λ2=-0.166 5-1.291 0i,λ3=-0.166 5+1.291 0i,是3个具有负实部的特征值,符合李雅普诺夫稳定性理论中的渐进稳定条件。因而E14′=(0.69, 0.58, 0.72)是博弈模型的均衡稳定策略(ESS)。这也同仿真模拟的结果相同。
根据上述分析,引入动态惩罚机制可以有效地避免博弈策略波动问题,并使得博弈策略达到稳定状态。
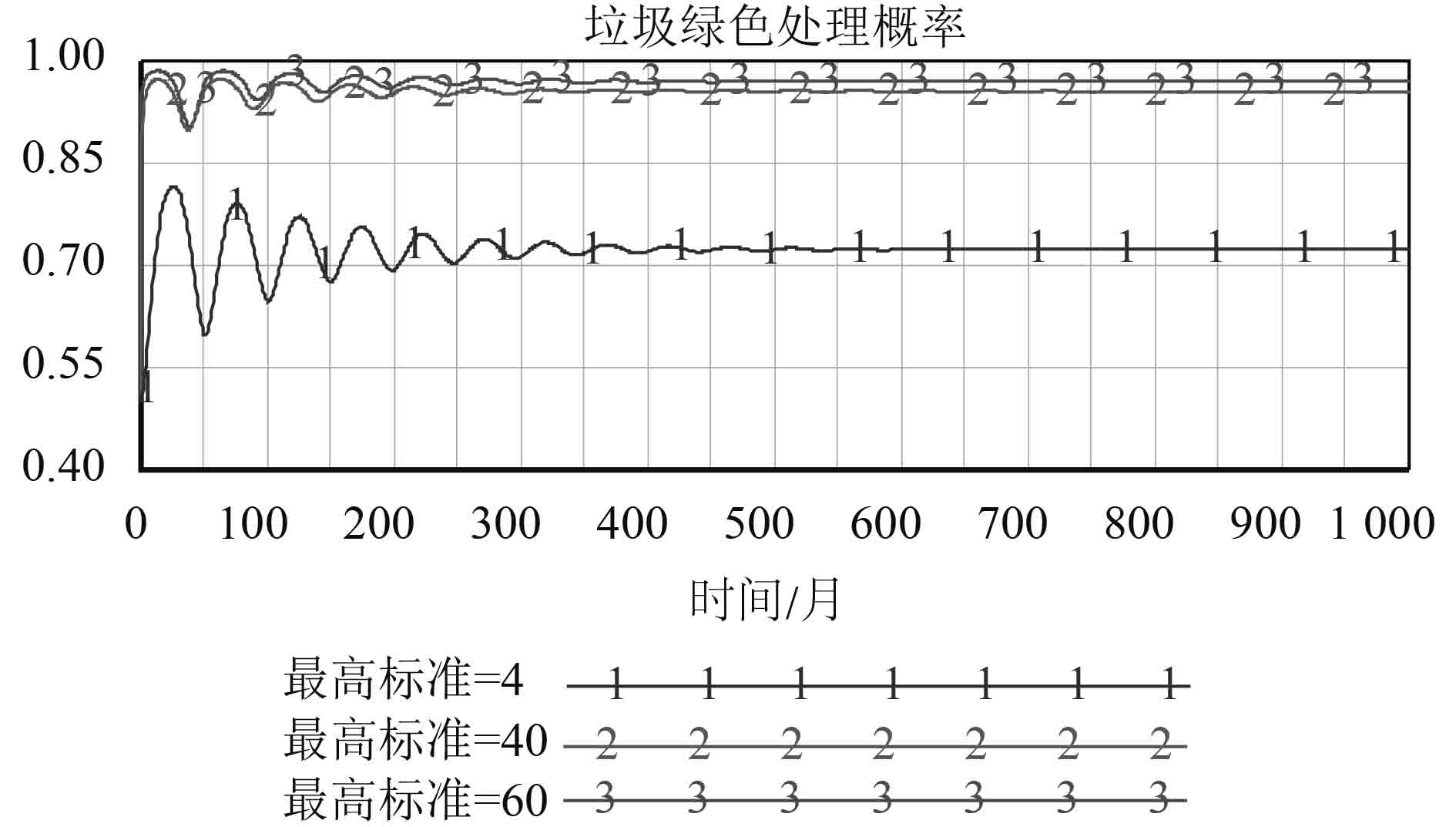
5.3 敏感性分析 5.3.1 企业最高罚金标准的敏感性分析上述分析结果虽然可以达到博弈模型的均衡稳定,但对于实际情况而言,仅仅72%的垃圾发电企业实行垃圾绿色处理以及58%的地方政府会采取监管,并不是理想中的均衡稳定策略。首先,仅将模型中企业的最高罚金分别改为40和60,代入模型进行仿真,结果如图10所示。由图10可知,通过提高对企业动态惩罚的最高标准,可以提高企业实行垃圾绿色处理的概率。
|
图 10 不同罚款最高标准下的垃圾绿色处理概率 Fig. 10 Waste green disposal probability under the different highest penalty standard |
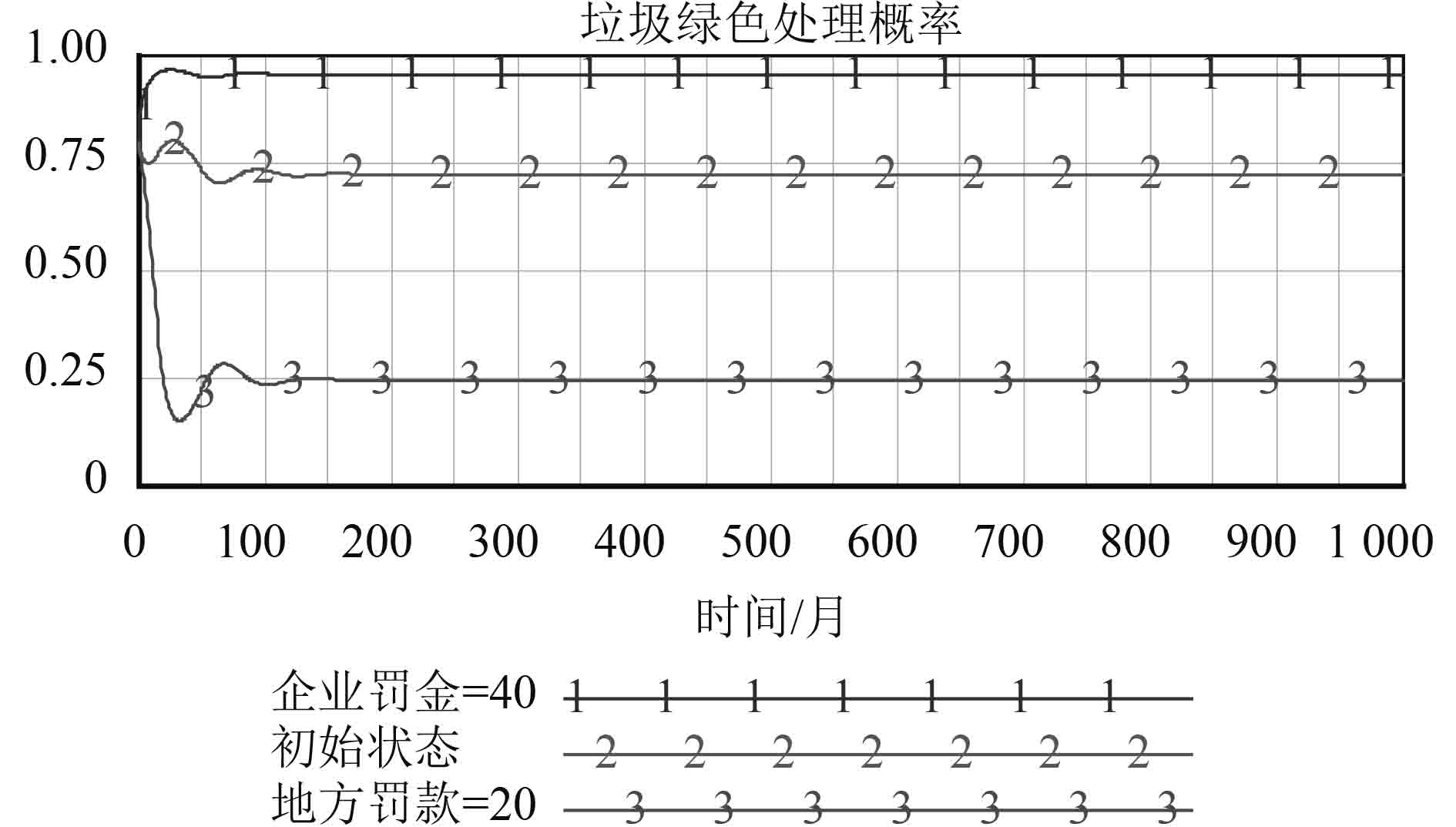
如果仅提高对地方政府的最高罚金,将其最高罚金标准改为20,代入模型仿真并将其同提高企业最高罚金标准进行比较,结果如图11所示。由图11可知,提高地方政府的罚金对于提高企业垃圾绿色处理概率并没有积极影响。相反,还会降低企业垃圾绿色处理概率。因为通过提高地方政府的最高罚金,会提高地方政府的监管概率。而企业可以通过贿赂,使得地方政府在监督过程中渎职,这样虽然监管概率提高了,但是降低了垃圾绿色处理概率。
|
图 11 提高地方和企业最高罚款标准的垃圾绿色处理概率 Fig. 11 Waste green disposal probability under raising the different highest penalty standard of local government and enterprise |
综上所述,要提高企业的垃圾绿色处理概率,最优的方法是提高对企业的最高处罚标准。如果将最高处罚标准提高到10倍,可以使得企业垃圾绿色处理概率趋近于1。
6 结论本文通过建立中央政府,地方政府以及垃圾焚烧发电企业关于垃圾绿色处理的三方博弈模型,并运用进化博弈论和系统动力学相结合的方法来分析三方策略的动态选择机制。通过上述研究结果,得出以下结论。
1)在现有模式下,中央政府、地方政府和垃圾焚烧发电企业的策略选择会呈现出波动的情况,即中央政府很难对垃圾焚烧发电企业是否采取绿色生产进行控制,无法很好地解决对环境的二次污染问题。
2)分别引入动态奖励策略和动态惩罚策略发现,当实施动态惩罚策略可以有效控制博弈三方的策略选择波动情况,获得进化稳定策略。通过敏感性分析,分别提高企业和地方政府的惩罚最高标准。通过比较发现,提高企业的最高处罚标准可以有效提高垃圾焚烧发电企业实行垃圾绿色处理的概率,使之趋近于1,达到理想的目标。
本文在研究过程中采用的仿真数据是在模拟的环境下完成的,并且时间单位也没有进行具体的设定,与实际情况有一定的差异,今后的研究将结合实际的数据进行仿真模拟,使得结果更加具有说服力。虽然政府采用动态惩罚机制可以实现最优控制,但是实际情况是很难对惩罚标准实行实时调整,因此具体的实施过程还需进一步研究。
| [1] |
中华人民共和国国家统计局. 中国统计年鉴[M]. 北京:中国统计出版社, 2004-2015.
National Bureau of Statistics of the People's Republic of China. China statistical yearbook[M]. Beijing: China Statistics Press, 2004-2015. |
| [2] |
唐龙, 唐一科. 垃圾发电产业化的一些问题及解决思路[J].
生态经济, 2007, 23(7): 114-116.
TANG Long, TANG Yike. Problems in the industrialization of refuse incineration-power generation and possible solutions[J]. Ecological Economy, 2007, 23(7): 114-116. |
| [3] | 中国砂石协会. “十三五”垃圾处理设施水平待提高[EB/OL](2016-03-04). http://www.zgss.org.cn/zixun/zhuti/ 1446.html, . |
| [4] | 熊孟清. 从“十三五”规划建议看我国垃圾处理转变[N]. 中国建设报, 2015-12-03(2). |
| [5] | PETTS J. Incineration risk perceptions and public concern: experience in the UK improving risk communication[J]. Waste Management & Resarch, 1992, 10(2): 169-182. |
| [6] | KALMYKOVA Y, FEDJE K K. Phosphorus recovery from municipal solid waste incineration fly ash[J]. Waste Management, 2013, 33(6): 1403-1410. DOI: 10.1016/j.wasman.2013.01.040. |
| [7] | FEDJE K K, EKBERG C, SKARNEMARK G. Initial studies of the recovery of Cu from MSWI fly ash leachates using solvent extraction[J]. Waste Management & Research, 2012, 30(10): 1072-1080. |
| [8] | SCHLUMBERGER S, BUEHLER J. Urban mining: metal recovery from fly and filter ash in waste to energy plants[C]. Stockholm, Sweden: ASH 2012. |
| [9] | BEYLOT A, VILLENEUVE J. Environmental impacts of residual Municipal Solid Waste incineration: A comparison of 110 French incinerators using a life cycle approach[J]. Waste Management, 2013, 33(12): 2781-2788. DOI: 10.1016/j.wasman.2013.07.003. |
| [10] | BOZORGIRAD M A, Hao Zhang, Karl R Haapala. Environmental impact and cost assessment of incineration and ethanol production as municipal solid waste management strategies[J]. The International Journal of Life Cycle Assessment, 2013, 18(8): 1502-1512. DOI: 10.1007/s11367-013-0587-z. |
| [11] | NIXONA J D, WRIGHT D G, DEY P K. A comparative assessment of waste incinerators in the UK[J]. Waste Management, 2013, 33(11): 2234-2244. DOI: 10.1016/j.wasman.2013.08.001. |
| [12] |
俞祖成, 庄秀娟. 我国公共决策中的利益诉求与利益博弈分析——以“番禺垃圾焚烧事件”为例[J].
广东广播电视大学学报, 2010, 19(81): 64-70.
YU Zucheng, ZHANG Xiujuan. The interests demands of the public decision-making and interests of the game——based on the panyu waste incineration incident[J]. Journal of Guangdong radio & TV University, 2010, 19(81): 64-70. |
| [13] |
刘承毅, 王建明. 声誉激励、社会监督与质量规制——城市垃圾处理行业中的博弈分析[J].
产经评论, 2014, 5(2): 93-106.
LIU Chengyi, WANG Jianming. Reputation incentive, social supervision and quality regulation——game analysis in the waste disposal industry[J]. Industrial Economic Review, 2014, 5(2): 93-106. |
| [14] |
李郁芳, 邱丹平. 基于利益集团理论的垃圾焚烧发电问题分析[J].
生态经济, 2010, 26(10): 149-152.
LI Yufang, QIU Danping. The analysis of refuse incinerating power generation problem from the perspective of interest groups[J]. Ecological Economy, 2010, 26(10): 149-152. |
| [15] | SMITH J M, PRICE G R. The logic of animal conflict[J]. Nature, 1973, 246(5427): 15-18. DOI: 10.1038/246015a0. |
| [16] | SELTEN R. Evolutionary stability in extensive two-person games[J]. Mathematical Social Sciences, 1983, 5(3): 269-363. DOI: 10.1016/0165-4896(83)90012-4. |
| [17] | HIRSHLEIFER J. Evolutionary Models in economics and law: cooperative versus conflict strategies[J]. Research in Law and Economics, 1982, 4: 1-60. |
| [18] | FRIEDMAN D. Economic applications of evolutionary game theory[J]. Journal of Evolutionary Economics, 1998, 8(1): 15-43. DOI: 10.1007/s001910050054. |
| [19] | TAYLOR P D, JONKER L B. Evolutionarily stable strategy and game dynamics[J]. Math Bioscience, 1978, 40(1-2): 145-156. DOI: 10.1016/0025-5564(78)90077-9. |
| [20] |
孙庆文, 陆柳, 严广乐. 不完全信息条件下演化博弈均衡的稳定性分析[J].
系统工程理论与实践, 2003, 23(7): 11-16.
SUN Qingwen, LU Liu, YAN Guangle. Asymptotic stability of evolutionary equilibrium under imperfect knowledge[J]. Systems Engineering - Theory & Practice, 2003, 23(7): 11-16. |
| [21] |
邱中华, 金栩. 基于进化博弈论研究一类监查博弈[J].
南京邮电大学学报:自然科学版, 2006, 26(5): 46-49.
QIU Zhonghua, JIN Xu. Study on a supervisory game based on evolutionary game theory[J]. Journal of Nanjing University of Posts and Telecommunications(Natural Science), 2006, 26(5): 46-49. |
| [22] |
蔡玲如, 王红卫, 曾伟. 基于系统动力学的环境污染演化博弈问题研究[J].
计算机科学, 2009, 36(8): 234-238.
CAI Lingru, WANG Hongwei, ZENG Wei. System dynamics model for a mixed-strategy game of environmental pollution[J]. Computer Science, 2009, 36(8): 234-238. |
| [23] |
达庆利, 张骥骧. 有限理性条件下进化博弈均衡的稳定性分析[J].
系统工程理论方法应用, 2006, 15(3): 279-284.
DA Qingli, ZHANG Jixiang. Stability of evolutionary equilibrium under bounded rationality[J]. Systems Engineering - Theory & Practice, 2006, 15(3): 279-284. |
| [24] |
魏芳芳, 陈福集. 三方非对称进化博弈行为分析[J].
浙江大学学报: 理学版, 2013, 40(2): 146-151.
WEI Fangfang, CHEN Fuji. A behavior analysis of evolutionary game under three asymmetric parties[J]. Journal of Zhejiang University(Science Edition),, 2013, 40(2): 146-151. |
| [25] |
刘连光, 刘鸿熹, 刘自发. 新能源接入下风火网三方非对称进化博弈分析[J].
中国科学: 技术科学, 2015, 45(12): 1297-1303.
LIU Lianguang, LIU Hongxi, LIU Zifa. Analysis of tripartite asymmetric evolutionary game among wind power enterprises, thermal power enterprises and power grid enterprises under new energy resources integrated[J]. Sci Sin Tech, 2015, 45(12): 1297-1303. |
| [26] |
特日昆, 徐飞. 战略性新兴产业信贷融资问题研究——基于银政企三方进化博弈视角[J].
管理现代化, 2015, 35(6): 22-24.
TE Rikun, XU Fei. Research on credit financing of strategic emerging industries-Based on the perspective of the evolution game three-side among bank, government and enterprises[J]. Modernization of Management, 2015, 35(6): 22-24. |
| [27] |
朱庆华, 窦一杰. 绿色供应链中政府与核心企业进化博弈模型[J].
系统工程理论与实践, 2007, 27(12): 85-95.
ZHU Qinghua, DOU Yijie. An evolutionary model between governments and core-enterprises in green supply chains[J]. Systems Engineering - Theory & Practice, 2007, 27(12): 85-95. |
| [28] |
章辉美, 邓子纲. 基于政府、企业、社会三方动态博弈的企业社会责任分析[J].
系统工程, 2011, 29(6): 123-126.
ZHANG Huimei, DENG Zigang. Analysis of corporate social responsibility based on three-side dynamic game between government, society and enterprises[J]. Systems Engineering, 2011, 29(6): 123-126. |
| [29] | 刘豹, 唐万生. 现代控制理论[M]. 北京:机械工业出版社, 2006. |
| [30] | LIU Quanlong, LI Xinchun, HASSALL M. Evolutionary game analysis and stability control scenarios of coal mine safety inspection system in China based on system dynamics[J]. Safety Science, 2015, 80: 13-22. DOI: 10.1016/j.ssci.2015.07.005. |
| [31] |
朱庆华, 王一雷, 田一辉. 基于系统动力学的地方政府与制造企业碳减排演化博弈分析[J].
运筹与管理, 2014, 23(3): 71-82.
ZHU Qinghua, WANG Yilei, TIAN Yihui. Analysis of an evolutionary game between local governments and manufacturing enterprises under carbon reduction policies based on system dynamics[J]. Operations Research and Management Science, 2014, 23(3): 71-82. |
 2017, Vol. 20
2017, Vol. 20