随着ERPⅡ的运用与发展,协同商务将供应链上下游企业结成一个利益整体,实现共同的战略目标,已经成为供应链运作最显著的特征。供应链运作可具体化为供应、生产、库存、销售、回收等各个环节的协调运作。早在1960年,Clark等[1]提出“级库存”概念,在单级库存的基础上增加多级库存,并建立无能力约束的多级库存分解方法。该方法奠定了多级库存问题的研究基础, 成为库存问题研究经典。本文将研究视角定位于供应链生产、库存环节,通过多级库存系统协同,或与生产等其他环节联合优化,是在激烈的供应链竞争之下,企业努力探寻的有效合作途径,以实现供应链最佳资源配置。
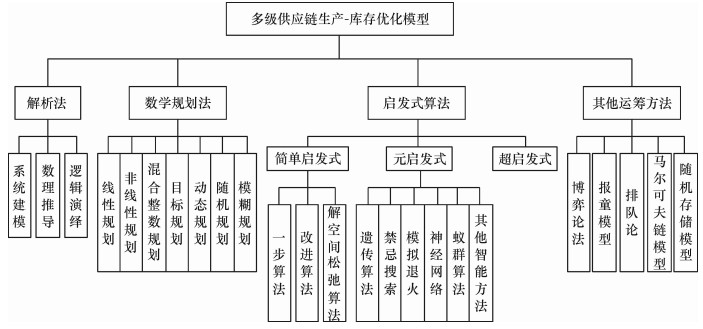
多级供应链生产-库存联合优化问题,始终是学术研究的重点与难点。通过优化模型抽象出数理分析的基础,将企业订货数量、订货周期、生产数量、库存数量等作为集中决策变量。由于供应链层级结构复杂,涉及多个成员,决策变量多样,对于优化模型的求解相对比较复杂。目前,常用的求解方法主要有解析法、数学规划法、启发式方法,以及其他运筹学方法,每种方法所包含的具体内容如图 1所示。
|
图 1 多级供应链生产-库存优化模型求解方法 Fig. 1 Solving method of optimization model for production-inventory in multi-level supply chain |
图 1所示优化模型求解方法是解决多级供应链生产-库存问题的重要工具。然而,目前基于模型求解方法视角对多级供应链生产-库存研究进行全面综述的文献很鲜见。因此,有必要对这一经典问题进行细致分析与回顾。本文对1960~2015年间国内外关于多级供应链生产-库存问题的代表性文献进行系统整理,其中绝大部分是近10年成果。以模型求解方法为标准分类总结,试图从方法论的角度梳理多级生产-库存问题的发展脉络,发现未来研究新趋势。
1 基于解析法的多级供应链生产-库存研究解析法(analytical method)又称分析法,是通过数学推导、逻辑演绎求解优化模型的方法,早期对于多级供应链问题的研究都采用此方法。Clark等[1]将级库存定义为某级仓库的在库存货数量,加上在途存货或者与该仓库有关的其他仓库现有存货,这些库存组成与特定仓库相关的等级。依据等级概念将多级仓库系统划分为多个单库存问题,通过递推计算得出使每级总折现成本最小的订货数量。在此基础上,Federgruen等[2]将Clark的两级两个位置的库存模型扩展到无限规划周期背景下,定期检查库存系统,且提前期固定,并结合一个仓库对多个位置配送问题,结果表明模型中的多个仓库位置可以用一个位置近似表达。Chen等[3]继续对一个仓库与多个零售商构成的分销网络的库存协同问题展开研究,其最大贡献在于得出比Clark分解方法更简化的推理证明过程来求解最优库存水平。如扩展研究周期,考察连续检查的(R, nQ)生产系统中两级生产-库存系统订货数量的协调,通过界定各层级关联库存关系,建立递归方程,计算出连续系统稳态的库存水平[4]。又如增加系统的持有成本与延迟交付成本,提出求解更长周期内由一个中心仓库和多个零售商组成的配送系统平均成本的解析算法[5]。当需求服从正态分布时,Clark分解法依然能够求解出多级供应链生产数量与订货批量的协调解[6]。
增加层级结构,或并行考虑更多库存约束因素时,既存的库存分解与模型解析方法被不断改进。Houtum等[7]将Clark的理论应用于一个三级连续的生产与分配系统中,研究随机需求下系统间物料协调问题,考虑等级间提前期与能力约束,放松约束条件后,库存分解方法依然有效。供应链的库存水平还可以与系统外的二级市场相结合,由于滞销品通过二级市场出售,原供应链系统的库存水平可以略高,通过对每一等级基本存货水平递归确定处置饱和策略,可以实现复杂系统的分解[8]。涉及期货市场的供应链库存管理问题,依然可以用此分解法进行推理,通过递推计算得出多级采购与分销系统在现货与期货两个市场的最优采购与分销策略的近似结果[9]。
线性代数或偏导方程等属于纯粹的数学分析法,近年也出现在研究文献中。Pal等[10]使用线性代数方程建立三级供应链的生产-库存模型,利用特征方程结合数学分析方法证明解存在并唯一,得出三级供应链的最佳订货量。Ghiami等[11]利用偏导方程法研究制造商与多买方组成的二级供应链生产数量与订货水平协同问题,偏导方程能够确定系统的唯一最优解。利用相似的方法,戢守峰等[12]不仅证明了制造商的生产数量与库存水平,还证明了碳约束机制对供应链生产与订货的影响。这两种方法得到的解都具有唯一性。
多级库存问题的研究始于解析法,时至今日依然沿用。随着研究对象的复杂程度增加,经典的Clark分解法不断发展,通过若干假设条件,抽象出现实问题的解析函数。虽然这些供应链组成结构相对简单,但推理分析复杂深入,可以有效地解决多级库存系统订货数量的协调问题。
2 基于数学规划法的多级供应链生产-库存研究随着大量实际问题的出现,解析法已不足以解决更复杂问题,需要借助于计算机技术,使得数学规划法(mathematical programming)成为研究多级生产-库存问题更实用的工具。通过约束条件,使优化模型取得最优值,这正是多级生产-库存系统在各种约束之下预期实现的目标。
线性规划是最常用的研究方法。通常情况下,顾客需求具有多样变化,在多级供应链中,需求不确定更符合客观实际。Kalchschmidt等[13]研究多级系统中不确定需求,每一层级上顾客的需求各不相同,根据需求波峰差距建立线性规划预测需求来管理各级库存水平。供应链的供给不足或存在供给中断风险,以及季节性消费品所导致的需求波动,通过线性规划模型,也可推理出供应链最优的订货数量[14]。按照库存数量的整数倍来安排生产计划,既保证供应链下游库存水平,又减少生产数量[15]。根据成本的线性依存关系,通过EOQ理论能够求解复杂供应链的生产与库存管理问题。Zavanella等[16]研究了单个卖方与多个买方的生产-库存问题,用EOQ模型推导出多个买方的订货周期以及卖方的订货周期,结果显示卖方以寄售形式管理多个买方库存是最好的选择。Park等[17]以零售商风险共享和供应商与分销商之间的提前期为因素研究三级供应链网络设计问题,用近似EOQ理论表示正态分布需求,可以简化库存控制模型。
非线性规划模型对于求解多级生产-库存问题同样适用。依据实际问题建立非线性规划模型,特别是单供应商对多销售商或单个仓库向多零售商配送问题,放松优化目标的假设条件,可得出系统最优的生产、供货以及配送策略。例如王圣东[18]与Li等[19]的研究。当问题规模变大时,对非线性规划模型进行技术处理是非常必要的。Tancrez等[20]将库存与选址问题结合,研究三级供应链网络决策问题,用近似替代法将不确定需求转化为确定需求处理,通过分解技术将模型转化为选址与库存两个线性规划进行求解。Jha等[21]采用拉格朗日乘数技术处理非线性约束,得出单个卖方与多个买方之间生产批量以及交付批次。
整数规划或混合整数规划是求解多级供应链优化模型的另一个重要的数学规划方法,特别是供应链结构达到四级以上。多成员与多层级间的整合,会由于变量以及参数过多造成求解困难。此时,分解技术作用更加突出。Pan等[22]建立有生产与运输能力约束的四级供应链混合整数规划,通过拉格朗日分解方法化简问题。Jonrinaldi等[23]所建立的五级制造供应链混合整数规划模型,通过层级分解技术,将模型转化为分散模型、半集中决策模型,以及集中决策模型进行研究。Guo等[24]建立了由多厂商构成的三级混合整数非线性规划模型,利用Benders技术分解为供应商选择与订单分配两个子模型,确定最优的策略。
除了上述几种方法以外,数学规划方法还包括目标规划、动态规划、随机规划以及模糊规划等。根据研究问题具体特性,选择恰当的规划模型是解决问题的关键。Guchhait等[25]用最优控制理论研究易碎品生产与库存控制,分别建立需求依赖时间与需求依赖于库存两个动态模型,以利润最大化作为控制目标。李群霞等[26]用模糊集理论研究带有缺货和缺陷产品的供应链生产库存模型,用梯级平均综合表示法进行解模糊处理。彭红军等[27]用随机模型研究了二级不确定环境下供应链的生产与订购决策,推理出集中决策时供应链利润更高。Omar等[28]研究三级准时制造系统,分别讨论等批量发货与等周期发货下供应商及买方持有成本最小的随机模型,用数学规划法得出最优的协调结果。
上述文献都是通过单目标优化模型得出结论,对于多目标决策问题,可以通过多目标规划模型权衡求解目标,寻找帕累托最优解。Lam等[29]在多级库存系统中引入供应商选择问题,基于系统成本与供应商质量双重目标,建立大规模的多目标线性规划(MOLP)模型,考虑从供应商到最终客户的满意程度,用图表的方式呈现帕累托最优解。卫忠等[30]建立需求满足率、时间、成本3个目标规划模型,研究了多级库存系统协同问题,利用演化多目标优化(EMOO)方法找出内外两层模型最优解,算例结果证明多目标优化效果更好。无论是单目标优化模型,还是多目标优化模型,都是各种数学规划法的组合运用。
3 基于启发式算法的多级供应链生产-库存研究启发式算法(heuristic algorithm)是相对于数学规划最优解而提出的。当无法得出模型准确解时,可根据实际问题设计出适用算法,在可接受的时间费用下得出合理范围内的可行解。启发式算法包括简单启发式、元启发式(metaheuristic)、超启发式(hyper-heuristic algorithm)3种。
早期的多级生产-库存问题主要采用简单启发式,利用迭代技术进行求解。Ben-Daya等[31]改变多级问题的理论分析,增加每一层级成员数量,建立的生产-库存整合模型,运用简单启发式迭代出最优的生产与订货数量。然而,此模型与算法被Cardenas-Barron等[32]进行改进,新的启发式算法不但节约CPU时间,也减少库存运营成本。启发式能够与各种模型、分解技术相结合,Rodriguez等[33]研究存在季节性需求波动的供应链库存管理与交付的优化模型,使用转换技术解决函数非凸问题,再利用简单启发式得出库存与交付的最优数量。还可以结合线性化、外逼近等分解技术形成新算法[34]。集中与分散是供应链两种决策方式,通常情况下,集中决策效果优于分散决策。分散决策模型求解相对容易,但集中决策时多采用启发式求解,设定步长,确定迭代步骤,得出近似的优化解,例如Sana[35]和Yu等[36]。然而Lee等[37]和Jaber等[38-39]还在集中决策结果之上,提出利润补偿系数、投资收益分配、数量折扣方法作为促进供应链协调的手段。
元启发式是启发式算法的改进,它将随机方法与局部搜索算法相结合,针对性更强。相对于简单迭代的启发式,元启发式包含的算法更多,例如遗传算法、禁忌搜索、模拟退火等智能优化方法。Efendigil等[40]以土耳其的伊斯坦布尔从事耐用消费品公司为例研究供应链整合方法,从消费者到供应商的仓库、零售商和工厂通过基于模糊推理系统的自适应网络和人工神经网络的方法整合,研究需求不确定下的供应商供给能力。Paul等[41]研究二级生产-库存系统的两种中断情景,分别建立系统单次和多次中断的库存模型,运用遗传算法求解多次中断的数学规划模型。Dettenbach等[42]研究多级库存系统中实时信息的价值,建立多级库存系统规划模型。模型特性表明对于中小规模问题,可以得出精确最优解。而对于大规模问题,需通过MULT-heuristic和OPT-heuristic两种启发式求解。
通过操纵或管理一组低层启发式算法,获得更高层次的新启发式算法,这就是超启发式算法。由于超启发式算法本身的研究处于探索阶段,使用此方法解决多级生产-库存问题的研究非常少。启发式算法所得到的解是确定最优解的近似表达,在一定程度上,并不能保证解的可行性与全局性,甚至无法准确阐述其与最优解之间的差异程度。但是,对于多层级、多约束、多变量、无法分解的非凸生产-库存优化模型,启发式或许是最好的选择。在可接受的计算时间或空间下,得出复杂问题的可行解。
4 基于其他运筹方法的多级供应链生产-库存研究还有一些优化模型的研究方法不属于上述范畴,而是采用其他运筹学方法求解,例如博弈论法、报童问题、马尔可夫链模型、随机存储模型、排队论等方法。
依据各成员的主体地位进行博弈,可以实现供应链内部均衡。通常在非合作博弈下,供应链中存在一个相对的领导者,例如海尔、沃尔玛,利用领导者的优势地位实行Stackelberg博弈,通过几个阶段的主从博弈之后,或者结合启发式求解方法,得出系统最优的生产数量或订货数量[43-44]。然而,非合作博弈并不一定是最好的选择,类似于供应链分散与集中决策方式一样,Sana[45]和Pal等[46]对供应链合作博弈展开研究,最终结果表明,合作博弈优于非合作博弈,但要建立有效的协调机制。
经典的报童模型,与博弈论法相结合,能够得出不同的研究结论。Seifert等[47]用报童模型研究风险中性的三级供应链协调形式,用期望利润最大化模型对比4种协调形式,结果表明上游协调优于下游协调。报童框架还可与分解技术结合,Shi等[48]用报童框架研究两个渠道产品的生产计划,用拉格朗日松驰法将模型分解成单产品子问题进行求解。报童模型更适用于三级供应链的库存管理问题,用以确定最优订货批量[49]。
当库存状态呈随机或离散时,排队论与马尔可夫链模型可求解此类问题。侯玉梅[50]利用排队论分析具有泊松需求的工厂与仓库之间协调问题,运用矩阵几何解论证系统达到稳定状态时的近似最优解。Muharremoglu等[51]研究了具有马尔可夫调节需求和随机提前期的多阶段基本库存策略的最优性,提出将多级系统分解成一系列单一产品单一顾客问题的新方法,并给出技术证明与计算基本库存水平的有效方法。Guerrero等[52]研究一个仓库,多个零售商的多产品分配系统库存联合优化问题,以现有库存价值最小为目标建立马尔可夫模型,使用启发式求出最大订货水平的近似最优解。Tai等[53]研究一个工厂、一个中心仓库和多个地方仓库构成的三级系统库存政策,建立使系统期望总成本最小的马尔可夫模型,最后用命题推理出转运数量与库存水平。
合作博弈与非合作博弈,形成了供应链分散与集中决策,各成员的影响能力在决策过程中发挥着重要作用,运用博弈论法可以得出不同主导能力的成员对策,所以博弈论法大量应用于多级生产-库存问题中。然而,运筹学包括的分支学科很多,优化模型求解方法越来越多样,这些方法为研究多级生产-库存问题提供参考。
5 研究评述与未来研究趋势经过几十年研究至今,多级生产-库存理论已经相对成熟。从上述文献分析来看,多级生产-库存的发展主要表现出以下特征。
1) 多级生产-库存理论研究不断深入。最早提出的级库存分解方法沿用至今,但分解方法本身却发生重大变化。然而,分解法依然是优化模型研究基础[54]。从解析模型到运用启发式算法求解的优化模型,模型的参数构成越来越复杂,模型约束条件也越来越严格。因此,多级生产-库存问题研究取得重大进展,形成完备的理论体系。
2) 数学规划法与启发式算法使用最广泛。从研究文献可以看出,虽然优化模型求解方法众多,但数学规划法与启发式算法却占据相当大的部分。数学规划法包含的各种规划形式,在确定的约束条件下,可以非常近似地表达现实库存问题。然而,约束条件过多会造成问题失真,或不存在确定的最优解,就需要结合问题设计适当的启发式算法,在可接受的条件下求解问题可行解。因此,这两种方法成为主要研究工具。
3) 其他运筹学方法同样适用多级系统问题,各种方法交叉运用更有效果。运筹学的分支有很多,在解决供应链多主体决策时,博弈论法、决策论法尤为适用。因此,出现大量文献运用博弈论分析方法,或者与其他方法相结合。例如,博弈论法与解析法相结合,在求解集成问题时,博弈论法与启发式算法并用。这种交叉现象随着问题的复杂程度,运用越来越广泛,运用数学规划法建立的复杂系统优化模型,需要设计特定的启发式算法才能得出优化解。还有一部分表现为数学规划法与解析法合并,这些方法交叉运用,能更有效地解决实际问题。
4) 供应链逐渐演变为层级增加、因素多样的复杂结构。早期的生产-库存理论分析大多以简单的供应链为基础,供应链由上下两级单个成员构成,主要考察上下级之间的库存与订货数量协调问题。然而,随着理论的深入,供应链层级结构扩展到三级、四级甚至五级,各级成员也不再是单一成员,而是多层级多成员的复杂结构。生产数量与库存水平仅是供应链决策的一个方面,涉及更多影响因素之间的协同。
从发展趋势来看,未来多级生产-库存问题研究可能在以下几个方面继续深入。
1) 研究问题将增加更多现实背景。现有文献的研究大部分局限于理论层面,少部分与现实问题结合。这是由于从现实背景中抽象出一般模型的过程相对复杂,如果不能准确度量约束关系,模型本身就失去意义,所以很多研究仅以虚拟算例进行模型验证。从辩证发展来看,理论研究要与实际相结合,从实际中修正理论模型,这样的研究才能更有学术生命力,为解决实际问题提供了可能。
2) 更复杂的学科交叉、各种求解方法交叉是未来研究多级系统问题的必然趋势。从前述分析看出,在多级生产-库存问题的研究方法上,数学规划法与启发式算法的应用最普遍。当前,越来越多的管理因素已经融入到供应链实践中,学科间的融合程度更加深入。所以,解决供应链问题的研究方法的交叉也将更加密集,超启发式算法也会逐渐应用到多级生产-库存中,以解决更复杂、更现实的供应链运作问题。
3) 供应链协作将更加突出。早有学者预言:未来竞争主要表现为供应链与供应链之间的竞争。所以,如何建立有利于供应链企业间的协调机制将有更现实的研究意义。同时,在多级生产-库存协调基础上,增加定价、供应商选择、风险偏好、环境约束等影响因素。利用已有的系统模型或协调机制,不断扩展出新的研究内容。
| [1] |
CLARK A J, SCARF H. Optimal policies for a multi-echelon inventory problem[J].
Management Science, 1960, 6(4): 475-490.
DOI: 10.1287/mnsc.6.4.475. |
| [2] |
FEDERGRUEN A, ZIPKIN P. Computational issues in an infinite horizon, multi-echelon inventory model[J].
Operations Research, 1984, 32(4): 818-836.
DOI: 10.1287/opre.32.4.818. |
| [3] |
CHEN F, ZHENG Y S. Lower bounds for multi-echelon stochastic inventory systems[J].
Management Science, 1994, 40(11): 1426-1443.
DOI: 10.1287/mnsc.40.11.1426. |
| [4] |
CHEN F, ZHENG Y S. Evaluating echelon stock (R, nQ) policies in serial production/inventory systems with stochastic demand[J].
Management Science, 1994, 40(10): 1262-1275.
DOI: 10.1287/mnsc.40.10.1262. |
| [5] |
CHEN F, ZHENG Y S. One-warehouse multi-retailer systems with centralized stock information[J].
Operations Research, 1997, 45(2): 275-287.
DOI: 10.1287/opre.45.2.275. |
| [6] |
夏海洋, 黄培清. 随机需求下提前期可控的生产-库存联合优化模型[J].
控制与决策, 2008, 06(6): 631-636.
XIA Haiyang, HUANG Peiqing. Integrated production-inventory model with stochastic demand and controllable lead time[J]. Control and Decision, 2008, 06(6): 631-636. |
| [7] |
HOUTUM G J V, INDERFURTH K, ZIJM W H M. Materials coordination in stochastic multi-echelon systems[J].
European Journal of Operational Research, 1996, 95(1): 1-23.
DOI: 10.1016/0377-2217(96)00080-X. |
| [8] |
ANGELUS A. A multi-echelon inventory problem with secondary market sales[J].
Management Science, 2011, 57(12): 2145-2162.
DOI: 10.1287/mnsc.1110.1419. |
| [9] |
GOEL A, GUTIERREZ G J. Multiechelon procurement and distribution policies for traded commodities[J].
Management Science, 2011, 57(12): 2228-2244.
DOI: 10.1287/mnsc.1110.1430. |
| [10] |
PAL B, SANA S S, CHAUDHURI K. A three layer multi-item production-inventory model for multiple suppliers and retailers[J].
Economic Modelling, 2012, 29(6): 2704-2710.
DOI: 10.1016/j.econmod.2012.08.022. |
| [11] |
GHIAMI Y, WILLIAMS T. A two-echelon production-inventory model for deteriorating items with multiple buyers[J].
International Journal of Production Economics, 2015, 159: 233-240.
DOI: 10.1016/j.ijpe.2014.09.017. |
| [12] |
戢守峰, 蓝海燕, 唐金环, 等. 碳限额与碳交易约束下制造商生产-库存控制策略[J].
运筹与管理, 2015(3): 51-59.
JI Shoufeng, LAN Haiyan, TANG Jinhuan, et al. Manufacturers of production-inventory control strategy under carbon cap-and-trade mechanism[J]. Operations Research and Management Science, 2015(3): 51-59. DOI: 10.12005/orms.2015.0083. |
| [13] |
KALCHSCHMIDT M, ZOTTERI G, VERGANTI R. Inventory management in a multi-echelon spare parts supply chain[J].
International Journal of Production Economics, 2003, 81/82: 397-413.
DOI: 10.1016/S0925-5273(02)00284-0. |
| [14] |
PAL B, SANA S S, CHAUDHURI K. A multi-echelon supply chain model for reworkable items in multiple-markets with supply disruption[J].
Economic Modelling, 2012, 29(5): 1891-1898.
DOI: 10.1016/j.econmod.2012.06.005. |
| [15] |
SAJADIEH M S, FALLAHNEZHAD M, KHOSRAVI M. A joint optimal policy for a multiple-suppliers multiple-manufacturers multiple-retailers system[J].
International Journal of Production Economics, 2013, 146(2): 738-744.
DOI: 10.1016/j.ijpe.2013.09.002. |
| [16] |
ZAVANELLA L, ZANONI S. A one-vendor multi-buyer integrated production-inventory model: the 'consignment stock' case[J].
International Journal of Production Economics, 2009, 118(1): 225-232.
DOI: 10.1016/j.ijpe.2008.08.044. |
| [17] |
PARK S, LEE T E, SUNG C S. A three-level supply chain network design model with risk-pooling and lead times[J].
Transportation Research Part E, 2010, 46(5): 563-581.
|
| [18] |
王圣东. 单供货商多销售商联合生产库存模型[J].
系统工程学报, 2006, 21(1): 92-96.
WANG Shengdong. Production inventory models for a one-vendor multi-buyer integrated system[J]. Journal of Systems Engineering, 2006, 21(1): 92-96. |
| [19] |
LI J X, CHU F, CHEN H X. Coordination of split deliveries in one-warehouse multi-retailer distribution systems[J].
Computers & Industrial Engineering, 2011(60): 291-301.
|
| [20] |
TANCREZ J S, LANGE J C, SEMAL P. A location-inventory model for large three-level supply chains[J].
Transportation Research Part E, 2012, 48(2): 485-502.
DOI: 10.1016/j.tre.2011.10.005. |
| [21] |
JHA J K, SHANKER K. Single-vendor multi-buyer integrated production-inventory model with controllable lead time and service level constraints[J].
Applied Mathematical Modelling, 2013, 37(4): 1753-1767.
DOI: 10.1016/j.apm.2012.04.042. |
| [22] |
PAN F, NAGI R. Multi-echelon supply chain network design in agile manufacturing[J].
Omega, 2013, 41(6): 969-983.
DOI: 10.1016/j.omega.2012.12.004. |
| [23] |
JONRINALDI N, ZHANG D Z. An integrated production and inventory model for a whole manufacturing supply chain involving reverse logistics with finite horizon period[J].
Omega, 2013, 41(3): 598-620.
DOI: 10.1016/j.omega.2012.07.001. |
| [24] |
GUO C, LI X P. A multi-echelon inventory system with supplier selection and order allocation under stochastic demand[J].
International Journal of Production Economics, 2014, 151: 37-47.
DOI: 10.1016/j.ijpe.2014.01.017. |
| [25] |
GUCHHAIT P, MAITI M K, MAITI M. Production-inventory models for a damageable item with variable demands and inventory costs in an imperfect production process[J].
International Journal of Production Economics, 2013, 144(1): 180-188.
DOI: 10.1016/j.ijpe.2013.02.002. |
| [26] |
李群霞, 张群. 考虑缺货和缺陷品的模糊生产库存模型的优化求解[J].
系统工程理论与实践, 2011, 31(3): 480-487.
LI Qunxia, ZHANG Qun. Fuzzy optimization of a production inventory system with allowable shortages and defective items[J]. Systems Engineering-Theory & Practice, 2011, 31(3): 480-487. DOI: 10.12011/1000-6788(2011)3-480. |
| [27] |
彭红军, 周梅华. 两级生产与需求不确定的供应链生产订购决策[J].
系统工程学报, 2010, 25(5): 622-628.
PENG Hongjun, ZHOU Meihua. Production and ordering decision in supply chain with uncertainty in two-echelon yields and demand[J]. Journal of Systems Engineering, 2010, 25(5): 622-628. |
| [28] |
OMAR M, SARKER R, OTHMAN W A M. A just-in-time three-level integrated manufacturing system for linearly time-varying demand process[J].
Applied Mathematical Modelling, 2013, 37(3): 1275-1281.
DOI: 10.1016/j.apm.2012.03.041. |
| [29] |
LAM S W, TANG L C. Multiobjective vendor allocation in multiechelon inventory systems: a spreadsheet model[J].
Journal of the Operational Research Society, 2006, 57(5): 561-578.
DOI: 10.1057/palgrave.jors.2602027. |
| [30] |
卫忠, 徐晓飞, 战德臣, 等. 协同供应链多级库存控制的多目标优化模型及其求解方法[J].
自动化学报, 2007, 33(2): 181-187.
WEI Zhong, XU Xiaofei, ZHAN Dechen, et al. Multi objective optimization model for collaborative multi-echelon inventory control in supply chain[J]. Acta Automatica Sinica, 2007, 33(2): 181-187. |
| [31] |
BEN-DAYA M, HARIGA M. Integrated single vendor single buyer model with stochastic demand and variable lead time[J].
International Journal of Production Economics, 2004, 92(1): 75-80.
DOI: 10.1016/j.ijpe.2003.09.012. |
| [32] |
CARDENAS-BARRON L E, TENG J T, TREVINO-GARZA G, et al. An improved algorithm and solution on an integrated production-inventory model in a three-layer supply chain[J].
International Journal of Production Economics, 2012, 136(2): 384-388.
DOI: 10.1016/j.ijpe.2011.12.013. |
| [33] |
RODRIGUEZ M A, VECCHIETTI A. Inventory and delivery optimization under seasonal demand in the supply chain[J].
Computers and Chemical Engineering, 2010, 34(10): 1705-1718.
DOI: 10.1016/j.compchemeng.2010.02.009. |
| [34] |
OSMAN H, DEMIRLI K. Economic lot and delivery scheduling problem for multi-stage supply chains[J].
International Journal of Production Economics, 2012, 136(2): 275-286.
DOI: 10.1016/j.ijpe.2011.12.001. |
| [35] |
SANA S S. A collaborating inventory model in a supply chain[J].
Economic Modelling, 2012, 29(5): 2016-2023.
DOI: 10.1016/j.econmod.2012.04.021. |
| [36] |
YU J C P, WEE H M, WANG K J. Supply chain partnership for three-echelon deteriorating inventory model[J].
Journal of Industrial and Management Optimization, 2008, 4(4): 827-842.
DOI: 10.3934/jimo. |
| [37] |
LEE J H, MOON K. Coordinated inventory models with compensation policy in a three level supply chain[C]. ICCSA'06 Proceedings of the 2006 International Conference on Computational Science and Its Applications -Volume Part Ⅲ, Heidelberg: Springer-Verlag Berlin, 2006.
|
| [38] |
JABER M Y, OSMAN I H, GUIFFRIDA A L. Coordinating a three-level supply chain with price discounts, price dependent demand, and profit sharing[J].
International Journal of Integrated Supply Management, 2006, 2(1/2): 28-48.
DOI: 10.1504/IJISM.2006.008337. |
| [39] |
JABER M Y, GOYAL S K. Coordinating a three-level supply chain with multiple suppliers, a vendor and multiple buyers[J].
International Journal of Production Economics, 2008, 116(1): 95-103.
DOI: 10.1016/j.ijpe.2008.08.001. |
| [40] |
EFENDIGIL T, ÖNÜT S. An integration methodology based on fuzzy inference systems and neural approaches for multi-stage supply-chains[J].
Computers & Industrial Engineering, 2012, 62(2): 554-569.
|
| [41] |
PAUL S K, SARKER R, ESSAM D. Real time disruption management for a two-stage batch production-inventory system with reliability considerations[J].
European Journal of Operational Research, 2014, 237(1): 113-128.
DOI: 10.1016/j.ejor.2014.02.005. |
| [42] |
DETTENBACH M, THONEMANN U W. The value of real time yield information in multi-stage inventory systems-exact and heuristic approaches[J].
European Journal of Operational Research, 2015, 240(1): 72-83.
DOI: 10.1016/j.ejor.2014.06.028. |
| [43] |
WANG K J, LIN Y S, YU J C P. Optimizing inventory policy for products with time-sensitive deteriorating rates in a multi-echelon supply chain[J].
International Journal of Production Economics, 2011, 130(1): 66-76.
DOI: 10.1016/j.ijpe.2010.11.009. |
| [44] |
HE Y, ZHAO X. Coordination in multi-echelon supply chain under supply and demand uncertainty[J].
International Journal of Production Economics, 2012, 139(1): 106-115.
DOI: 10.1016/j.ijpe.2011.04.021. |
| [45] |
SANA S S. A production-inventory model of imperfect quality products in a three-layer supply chain[J].
Decision Support Systems, 2011, 50(2): 539-547.
DOI: 10.1016/j.dss.2010.11.012. |
| [46] |
PAL B, SANA S S, CHAUDHURI K. Three-layer supply chain-a production-inventory model for reworkable items[J].
Applied Mathematics and Computation, 2012, 219(2): 530-543.
DOI: 10.1016/j.amc.2012.06.038. |
| [47] |
SEIFERT R W, ZEQUEIRA R I, LIAO S Q. A three-echelon supply chain with price-only contracts and sub-supply chain coordination[J].
International Journal of Production Economics, 2012, 138(2): 345-353.
DOI: 10.1016/j.ijpe.2012.04.006. |
| [48] |
SHI J M, ZHANG G Q, SHA J C. Optimal production planning for a multi-product closed loop system with uncertain demand and return[J].
Computers & Operations Research, 2011, 38(3): 641-650.
|
| [49] |
ROY A, SANA S S, CHAUDHURI K. Optimal replenishment order for uncertain demand in three layer supply chain[J].
Economic Modelling, 2012, 29(6): 2274-2282.
DOI: 10.1016/j.econmod.2012.07.008. |
| [50] |
侯玉梅. 简单生产-库存系统的优化控制[J].
系统工程理论与实践, 2003(4): 1-6.
HOU Yumei. The optimal control of a simple inventory-production system[J]. Systems Engineering-Theory & Practice, 2003(4): 1-6. |
| [51] |
MUHARREMOGLU A, TSITSIKLIS J N. A single-unit decomposition approach to multi-echelon inventory systems[J].
Operations Research, 2008, 56(6): 1089-1103.
|
| [52] |
GUERRERO W J, YEUNG T G, GUÉRET C. Joint-optimization of inventory policies on a multi-product multi-echelon pharmaceutical system with batching and ordering constraints[J].
European Journal of Operational Research, 2013, 231(1): 98-108.
DOI: 10.1016/j.ejor.2013.05.030. |
| [53] |
TAI A H, CHING W K. Optimal inventory policy for a Markovian two-echelon system with returns and lateral transshipment[J].
International Journal of Production Economics, 2014, 151: 48-55.
DOI: 10.1016/j.ijpe.2014.01.010. |
| [54] |
KOVACS A, EGRI P, KIS T, et al. Inventory control in supply chains: alternative approaches to a two-stage lot-sizing problem[J].
International Journal of Production Economics, 2013, 143(2): 385-394.
DOI: 10.1016/j.ijpe.2012.01.001. |
 2016, Vol. 19
2016, Vol. 19