2. 重庆大学 经济与工商管理学院,重庆 400044
2. School of Economics and Business Administration, Chongqing University, Chongqing 400044, China
商业信用是指供应商给零售商在货款支付期限方面的优惠,在延期支付期限内买方不需要支付利息。它是公司短期外部融资一个重要渠道,广泛地存在于商业活动中。国内外学者对于供应链中商业信用的研究大部分是基于经济订货批量框架进行的,针对商业信用下的供应链协调的研究还不多。Jaber等[1]对供应链在商业信用下的协调及利润分配进行了研究。Sarmah等[2]对单个供应商和单个零售商在商业信用下的利润分享进行了研究,并比较了商业信用和价格折扣策略。Chen等[3]研究了存在缺陷产品情况下商业信用对供应链的协调作用。Chang等[4]研究了供应商利用商业信用这个工具使供应链达到了协调。Luo等[5]研究了在信息对称和不对称情况下商业信用对供应链的协调作用。于丽萍等[6]分析了供应链中商业信用的激励作用。张钦红等[7]分析了在不完全信息下制造商向零售商提供基于采购量的交易信用,实现供应链的协调。李群霞等[8]在库存模型中引入商业信用机制来平衡供应链各成员的利益。王志宏等[9]研究了基于商业信用和收入共享组合式合同的集成服务提供商与客户企业间的协调问题。
闭环供应链的研究方面,Savaskan等[10]研究了闭环供应链的渠道结构问题,证明了在其假设条件下经销商负责逆向物流是最优的渠道。Bhattacharya等[11]研究了零售商分别向制造商订新产品和向再制造商订再造品的最优订单数量问题。Kaya[12]研究了不确定环境下再制造闭环供应链的生产决策和激励协调问题。葛静燕等[13]基于博弈论方法分析了闭环供应链定价策略。公彦德等[14]引入了第三方物流服务商,分析了物流费用的分担比例对闭环供应链利润的影响。易余胤等[15]在销售渠道和回收渠道存在冲突的情形下研究闭环供应链的博弈协调模型。覃艳华等[16]分析了努力弹性系数与成本同时扰动时的闭环供应链协调问题。孔造杰等[17]研究了由制造商、回收维修中心及零售商构成的三级闭环供应链的定价决策和协调策略。
在闭环供应链有关收益共享契约的研究方面,Yadav等[18]通过实证研究发现收益共享契约可以增加闭环供应链上各成员的利润。王玉燕[19]分析了收益共享契约对闭环供应链突发事件的协调作用。孙浩等[20]研究了收益共享契约对两周期再制造闭环供应链的协调问题。史成东等[21]证明了收益共享契约和批量折扣契约均能使loss-averse闭环供应链达到协调。王雷等[22]设计了收益共享契约,实现了制造商回收再制造闭环供应链的协调和优化。李新然等[23]设计了可协调3种不同渠道权力结构的分散式决策闭环供应链的收益共享契约。高鹏等[24]提出了收益共享和费用分担的协作机制来协调三级闭环供应链系统。
鉴于商业信用在实践中的普遍存在,本文将商业信用作为一种新的协调机制引入到闭环供应链中,先分析了分散决策模式和集中决策模式下的定价策略,接着设计了基于商业信用的协调机制。
1 问题描述与符号说明本文考虑一个制造商和一个零售商,模型分为两周期,产品销售期和产品回收期。在产品销售期,制造商制造的产品通过零售商销售给消费者。在产品回收期,制造商委托零售商回收废旧产品,以一定的价格从零售商处把废旧产品购买回来进行再制造。假设再制造产品和新产品在质量和功能上完全相同,消费者对两者的接受度也完全相同。
p1为单位产品的销售价格。
p2为零售商从消费者手中回收废旧产品时的单位回收价格。
ω为单位产品的批发价格。
cm为制造商用全新的原材料进行生产的单位成本。
cr为制造商用回收的废旧产品为原材料进行生产的单位生产成本,cm≥cr,令Δ=cm-cr。
c1,c2分别表示零售商销售产品和回收废旧产品时的正向、逆向边际运营成本(如库存成本、运输成本等)。
b为制造商支付给零售商的单位回收产品的转移价格。
D为产品的市场需求量。D=Q-ap1>0,其中,Q是市场潜在需求,a为消费者对价格的敏感系数。
G为废品的回收量。G=k+hp2>0,其中,k>0是度量社会环保意识的指标,表示存在着k数量的消费者愿意无偿返还使用后的产品;h>0代表了消费者对回收价格的敏感程度[13-14]。
M为商业信用期,单位为年。
I为全社会的年化平均投资收益率,表示为百分比比率。
η为废旧产品回收期利润的时间折现率,η∈(0, 1]。
πm,πr,π分别为制造商、零售商以及整条供应链的利润。
2 分散模式下的定价决策供应链各主体按照Stackelberg主从博弈进行决策。制造商制定产成品的批发价ω和废旧品的单位回收价b,然后,零售商根据制造商的定价来制定单位产品的销售价格p1和单位废旧产品的回收价格p2。此时,零售商和制造商的利润目标函数分别为:
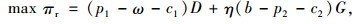
|
(1) |
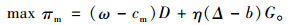
|
(2) |
式(1)、(2)等号右边第1项和第2项分别表示零售商和制造商在产品销售期和产品回收期的利润。
利用逆向归纳法,先分析零售商的定价策略,后求解制造商的定价策略。易证零售商的利润函数式(1)关于p1,p2的海塞矩阵是负定矩阵,所以式(1)是关于p1,p2的联合凹函数。令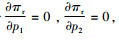
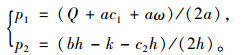
|
(3) |
将式(3)代入制造商的利润函数式(2),易证式(2)关于ω、b的海塞矩阵是负定矩阵,所以式(2)是关于ω、b的联合凹函数。令πm/ω=0,πm/b=0,同时结合式(3),可以求得零售商和制造商在分散决策模式下最优定价策略(用上标“d”表示零售商和制造商在分散决策时的最优定价策略)。
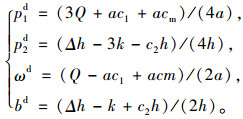
|
(4) |
此时,零售商和制造商的利润分别为:
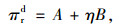
|
(5) |
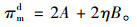
|
(6) |
其中,A=(Q-ac1-acm)2/(16a),B=(Δh+k-c2h)2/(16h)。
分析上述结果可以知道,新产品的销售价格与新产品制造成本以及销售成本有关,不受逆向物流的影响。废旧产品的回收价格与新产品制造成本、再制造成本以及零售商的废旧产品回收成本有关,受到正向和逆向物流的影响。产品的批发价与零售商的销售成本和新产品的制造成本有关,不受逆向物流影响。废旧产品的转移价格与新产品制造成本、再制造成本以及废旧产品回收成本有关,受到正向和逆向物流的影响。
3 集中模式下供应链的定价决策在集中决策模式下,供应链的利润目标函数
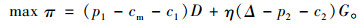
|
(7) |
易证式(7)关于p1和p2的海塞矩阵是负定矩阵,所以式(7)是关于p1和p2的联合凹函数。式(7)关于p1和p2求导并令其等于0,得到最优定价决策,用上标“c”表示集中决策时的最优结果。
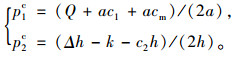
|
(8) |
整条供应链的利润为πc=4A+4ηB
定理1 1)p1d>p1c,p2d < p2c;2) Dd< Dc,Gd < Gc;3) πrd+πmd < πc。
证明 1)把式(8)分别代入D=Q-ap1>0,G=k+hp2>0可得Q-ac1-acm>0,Δh+k-c2h>0。p1d-p1c=(Q-ac1-acm)/(4a)>0,p2c-2d=(Δh+k-c2h)/(4h)>0。
2) D=Q-ap1,G=k+hp2,结合1)的结果,可以得到Dd < Dc,Gd < Gc。
3) πc-(πrd+πmd)=A+ηB>0,所以,πrd+πmd < πc。
定理1表明,集中决策在增加供应链系统利润的同时,也增加整个社会的效益和福利。因为相对于分散决策模式,在集中决策模式下供应链商品零售价下降,销量增加,更好地满足了消费者的需求,社会总福利增加。在集中模式下废旧产品的回收价提高了,增加了废旧产品的回收量,节约了社会资源,也有利于整个社会的环保事业。
4 闭环供应链协调策略设计为了使供应链达到协调,设计了基于商业信用的闭环供应链协调机制。在商品的销售阶段,制造商提供商业信用给零售商,零售商从制造商处订购商品的货款(ωD)可以延迟一段时间(M)后支付,在延期支付期限M内零售商不需要支付利息,即零售商的收益增加了IωDM,同时制造商以(1-φ)的比例分享零售商销售阶段的收益。
零售商和制造商的利润函数分别为:
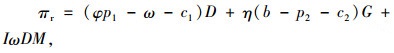
|
(9) |
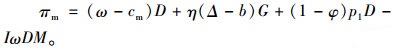
|
(10) |
利用逆向归纳法,首先分析零售商的决策。易证式(9)关于p1、p2的海塞矩阵是负定矩阵,所以式(9)是关于p1、p2的联合凹函数,由πr/p1=0,πr/p2=0,可以求得零售商的反应函数:
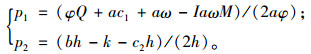
|
(11) |
将式(11)代入式(10)后,易证式(10)关于ω和b的海塞矩阵是负定矩阵,所以式(10)是关于ω和b的联合凹函数,令πm/ω=0,πm/b=0,同时结合式(11),可求得零售商和制造商的最优决策(用上标“*”表示零售商和制造商此时的最优决策)。
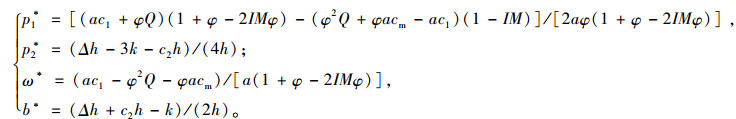
|
(12) |
定理2 当契约参数满足ω=[φcm-(1-φ)c]/(1-IM),b=Δ时,整条闭环供应链达到协调。
证明 当商品的销售价p1*和废旧产品的回收价p2*分别等于集中决策时商品销售价p1c和废旧产品的回收价p2c时,整条闭环供应链就达到协调。解方程组p1*=p1c,p2*=p2c可以得到:
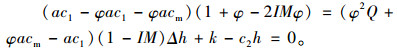
|
结合式(12)进行化简,可得ω=[φmc-(1-φ)c]/(1-IM),b=Δ。
此时,零售商、制造商和供应链的利润分别为:
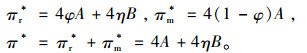
|
定理3 当供应链协调时,且收益分配参数满足(A-3ηB)/(4A)≤φ≤(A-ηB)/(2A,零售商和制造商都愿意接受契约。
证明 当零售商和制造商在协调时的利润不小于他们在分散决策时的收益时,零售商和制造商都愿意接受契约。
由πr*≥πrd,即4φA+4ηB≥A+ηB,可得φ≥(A-3ηB)/(4A);
由πm*≥πmd,4(1-φ)A≥2A+2ηB,可得φ≤(A-ηB)/(2A)。
推论1 当供应链协调时,商品的批发价ω随着商业信用期M和收益分配比例φ的增加而增加,商品销售价p1则随着商业信用期M和收益分配比例φ的增加而减小。
当商业信用期M或收益分配比例φ增加时,制造商在利益分配中处于更不利的位置,所以,制造商会通过提高批发价来弥补,从而达到平衡和协调。而此时在利益分配中处于更有利位置的零售商则可以降低产品的销售价,以吸引更多的顾客。
推论2 供应链协调时,零售商能接受的最小收益分配比例φ1=(A-3ηB)/4A随着折现率的减小而增大。
当折现率较小时,未来的收益相对变少,吸引力减弱,这就要求增大现阶段的收益来弥补,当折现率较大时,未来的收益相对变大,吸引力增强,那么零售商可以接受比较小的收益分配比例。
如果一个企业的发展有长远计划、长期的远景规划时,其折现率就会表现得比较高;当只有短期计划,缺少长期计划,没有长期的远景规划时,其折现率就表现得比较低[25]。所以当企业发展只有短期计划时,折现率就会比较低,此时零售商要求的最低收益比例就会增加,这样供应链就相对更难达成协调。当企业发展有长远计划和远景规划时,其折现率相对较高,零售商要求的最低收益比例就会降低,此时,更有利于供应链双方达成一致。所以供应链在寻找合作伙伴时,尽可能选择有长期计划的企业作为合作伙伴,更有利于供应链的协调和长期合作。
5 算例分析下面通过一些数值算例来验证以上模型的有关结论。假设有关参数赋值如下:cm=50,cr=20,c1=1,c2=2,Q=500,a=3,k=10,h=5,η=0.8,I=7%。
表 1表明,集中决策时的商品销售价低于分散决策时的销售价,销量也由86.75增加到173.51,满足了更多的消费者,增加了社会总福利。同时集中决策模式下供应链废旧产品的回收价高于分散决策时的回收价,废旧产品的回收量由37.5增加到75,资源利用率得到大幅度的提升,节约了社会资源,有利于整个社会的环保事业。
| 表 1 分散决策和集中决策时的定价和利润 Tab. 1 Pricing and profit in decentralized and centralized decision |
同时,在分散决策模式下供应链总利润为8 200.50,低于集中决策时的供应链总利润10 934.00,说明分散决策时的供应链没有达到协调,整体利润还有提升空间。
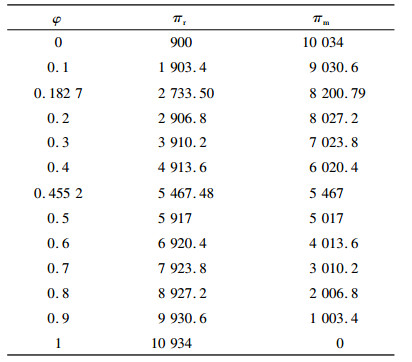
从表 2可以看到,零售商的利润随着收益分配比例φ的增大而增大,当φ增大到0.182 7时,零售商的利润为2 733.50,正好等于零售商在分散决策时的利润,所以零售商能接受的最低收益分配比例为0.182 7。制造商的利润随着收益分配比例φ的增大而减小,当φ值为0.455 2时,制造商的利润为5 467,正好等于制造商在分散决策时的利润。所以,制造商所能接受的最高收益分配比例为0.455 2。当0.182 7≤φ≤0.455 2时,供应链才有可能实现协调。
| 表 2 收益分配比例对零售商和制造商利润的影响 Tab. 2 The influence of income distribution proportion on profits of retailer and manufacturer |
图 1说明了商品的批发价ω随着商业信用期M和收益分配比例φ的增加而增加,这可以解释为,当商业信用期和收益分配比例增加时,零售商的利润增加,制造商的利润减少,制造商通过设置更高的批发价来弥补一部分损失,从而达到平衡和协调。
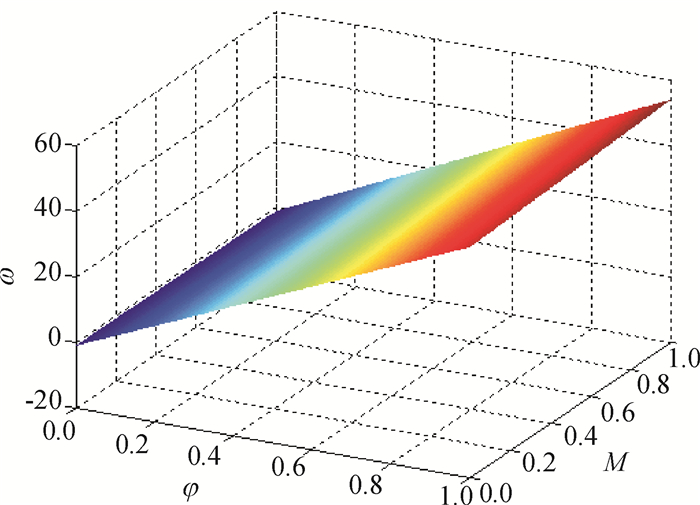
|
图 1 商业信用长度M和收益分配比例φ对批发价的影响 Fig. 1 The influence of trade credit length and proportion of income distribution on wholesale price |
本文把商业信用作为一种新的协调机制引入到闭环供应链中。首先研究了分散决策和集中决策时的定价决策,相对于分散决策,集中决策时的商品销售价降低了,废旧产品的回收价提高了。所以,产品的销量和废旧产品的回收量都增加了,从而满足了更多的消费者,提高了资源利用率,增加了社会总福利。为了消除双重边际效应带来的供应链失调,本文提出了基于商业信用和收益共享的协调机制,使得分散决策下的零售商和制造商的利润以及消费者和社会的效用都得到了提高,实现了供应链协调。
本文还可以从以下方面进行扩展。首先,可以考虑商业信用在制造商或第三方负责回收的闭环供应链的协调机制设计。其次,可以考虑零售商和制造商的年化投资收益率不同的情况下的协调机制设计。最后,还可以把商业信用跟其他协调契约结合起来研究闭环供应链的协调机制设计。
| [1] |
JABER M Y, OSMAN I H. Coordinating a two-level supply chain with delay in payments and profit sharing[J].
Computers & Industrial Engineering, 2006, 50(4): 385-400.
|
| [2] |
SARMAH S P, ACHARYA D, GOYAL S K. Coordination and profit sharing between a manufacturer and a buyer with target profit under credit option[J].
European Journal of Operational Research, 2007, 182(3): 1469-1478.
|
| [3] |
CHEN L H, KANG F S. Coordination between vendor and buyer considering trade credit and items of imperfect quality[J].
International Journal of Production Economics, 2010, 123(1): 52-61.
|
| [4] |
CHANG H L, BYONG-DUK R. Trade credit for supply chain coordination[J].
European Journal of Operational Research, 2011, 214(1): 136-146.
|
| [5] |
LUO J, ZHANG Q. Trade credit: a new mechanism to coordinate supply chain[J].
Operations Research Letters, 2012, 40(5): 378-384.
DOI: 10.1016/j.orl.2012.04.008. |
| [6] |
于丽萍, 黄小原, 邱若臻. 基于商业信用的收入共享契约与供应链协调[J].
运筹与管理, 2009, 18(1): 42-46.
YU Liping, HUANG Xiaoyuan, QIU Ruozhen. Supply chain coordination and revenue sharing contract based on trade credit[J]. Operations Research and Management Science, 2009, 18(1): 42-46. |
| [7] |
张钦红, 骆建文. 双边不完全信息下的供应链信用期激励机制[J].
系统工程理论与实践, 2009, 29(9): 32-40.
ZHANG Qinhong, LUO Jianwen. Coordination of supply chain with trade credit under bilateral information asymmetry[J]. Systems Engineering-Theory & Practice, 2009, 29(9): 32-40. DOI: 10.12011/1000-6788(2009)9-32. |
| [8] |
李群霞, 王文彬, 张群. 供应链库存商业信用协调的研究[J].
中国管理科学, 2013, 21(2): 58-65.
LI Qunxia, WANG Wenbin, ZHANG Qun. Coordinating a supply chain with trade credit[J]. Chinese Journal of Management Science, 2013, 21(2): 58-65. |
| [9] |
王志宏, 邵奇明, 袁袁. 商业信用和收入共享组合合同下集成服务提供商与其客户间的协调[J].
管理工程学报, 2015, 29(1): 143-148.
WANG Zhihong, SHAO Qiming, YUAN Yuan. Coordination between ISP and client enterprises under the combination contract with tract credit and revenue sharing[J]. Journal of Industrial Engineering / Engineering Management, 2015, 29(1): 143-148. |
| [10] |
SAVASKAN R C, BHATTACHARYA S, WASSENHOVE L N. Closed-loop supply chain models with product remanufacturing[J].
Management Science, 2004, 50(2): 239-252.
|
| [11] |
BHATTACHARYA S, GUIDE V D R, WASSENHOVE L N. Optimal order quantities with remanufacturing across new product generations[J].
Production and Operations Management, 2006, 15(3): 421-431.
|
| [12] |
KAYA O. Incentive and production decisions for remanufacturing operations[J].
European Journal of Operational Research, 2010, 201(2): 442-453.
|
| [13] |
葛静燕, 黄培清. 基于博弈论的闭环供应链定价策略分析[J].
系统工程学报, 2008, 23(1): 111-115.
GE Jingyan, HUANG Peiqing. Price decision analysis for closed-loop supply chain based on game theory[J]. Journal of Systems Engineering, 2008, 23(1): 111-115. |
| [14] |
公彦德, 李帮义, 刘涛. 基于物流费用分摊比例的闭环供应链模型[J].
系统工程学报, 2011, 26(1): 39-49.
GONG Yande, LI Bangyi, LIU Tao. Model for closed-loop supply chain based on the loading ratio of logistics cost[J]. Journal of Systems Engineering, 2011, 26(1): 39-49. |
| [15] |
易余胤, 袁江. 渠道冲突环境下的闭环供应链协调定价模型[J].
管理科学学报, 2012, 15(1): 54-65.
YI Yuyin, YUAN Jiang. Pricing coordination of closed-loop supply chain in channel conflicts environment[J]. Journal of Management Science in China, 2012, 15(1): 54-65. |
| [16] |
覃艳华, 曹细玉, 陈本松. 努力弹性系数与成本同时扰动的闭环供应链协调应对研究[J].
中国管理科学, 2015, 23(5): 41-47.
QIN Yanhua, CAO Xiyu, CHEN Bensong. Closed-loop supply chain coordination when effort elasticity coefficient and production cost disruptions simultaneously[J]. Chinese Journal of Management Science, 2015, 23(5): 41-47. |
| [17] |
孔造杰, 李伟, 张亚萍. 价格差异的三级闭环供应链定价与协调策略[J].
工业工程, 2015, 18(1): 90-95.
KONG Zaojie, LI Wei, ZHANG Yaping. Strategy of pricing and coordination for three-stage closed-loop supply chain with differential price[J]. Industrial Engineering Journal, 2015, 18(1): 90-95. |
| [18] |
YADAV P, MILLER D M, SCHMIDT C P. McGriff treading company implements service contracts with shared savings[J].
Interfaces, 2003, 33(6): 18-29.
|
| [19] |
王玉燕. 收益共享契约下闭环供应链应对突发事件的协调分析[J].
中国管理科学, 2009, 17(6): 78-83.
WANG Yuyan. Closed-loop supply chain coordination under disruptions with revenue-sharing contract[J]. Chinese Journal of Management Science, 2009, 17(6): 78-83. |
| [20] |
孙浩, 达庆利. 基于产品差异的再制造闭环供应链定价与协调研究[J].
管理学报, 2010, 7(5): 733-738.
SUN Hao, Qingli DA. Pricing and coordination of remanufacturing closed-loop supply chain based on product differentiation[J]. Chinese Journal of Management, 2010, 7(5): 733-738. |
| [21] |
史成东, 陈菊红, 郭福利, 等. Loss-averse闭环供应链协调[J].
系统工程理论与实践, 2011, 31(9): 1668-1673.
SHI Chengdong, CHEN Juhong, GUO Fuli, et al. On closed-loop supply chain coordination with loss-averse retailer[J]. Systems Engineering-Theory & Practice, 2011, 31(9): 1668-1673. DOI: 10.12011/1000-6788(2011)9-1668. |
| [22] |
王雷, 史成东. 经济政策对制造商回收的闭环供应链影响分析[J].
工业工程, 2011, 14(5): 19-23.
WANG Lei, SHI Chengdong. On the effect of economic policies on closed-loop supply chain with manufacturer collection[J]. Industrial Engineering Journal, 2011, 14(5): 19-23. |
| [23] |
李新然, 牟宗玉, 宋志成. 基于博弈论的制造商回收再制造闭环供应链模型研究[J].
科研管理, 2013, 34(9): 64-71.
LI Xinran, MU Zongyu, SONG Zhicheng. Research on manufacturers' collecting and remanufacturing the closed-loop supply chain model based on the game theory[J]. Science Research Management, 2013, 34(9): 64-71. |
| [24] |
高鹏, 谢印成, 高杰. 考虑专利许可费的三级闭环供应链协作机制[J].
工业工程, 2013, 16(4): 14-19.
GAO Peng, XIE Yincheng, GAO Jie. Three-level closed loop supply chain coordination mechanism with patent license fee considered[J]. Industrial Engineering Journal, 2013, 16(4): 14-19. |
| [25] |
CHU W, DESAI P S. Channel coordination mechanisms for customer satisfaction[J].
Marketing Science, 1995, 14(4): 343-359.
|
 2016, Vol. 19
2016, Vol. 19