2. 南京大学 工程管理学院,江苏 南京 210093
2. School of Management Science and Engineering, Nanjing University, Nanjing 210093, China
零售商主导型供应链是近年来供应链协调优化研究的热点问题之一。现实中,大型零售商作为接触消费者的第一环节,能及时掌握市场信息的变化,在供应链中常占据着主导地位。因此,研究由零售商主导的供应链系统具有现实意义。目前,对于零售商主导的供应链协调机制,已有不少研究成果,如Hua等[1]、Li等[2]均采用不同契约研究了零售商主导下的供应链协调问题。
自Kleindorfer等[3]提出了期权合同价格应包括期权价格和执行价格后,很多学者研究了与期权契约相关的供应链协调问题。例如,Luo等[4]和Chen等[5]。但上述研究期权契约的文献主要集中在生产商/供应商主导的供应链研究,而零售商主导的供应链研究文献还不多。如Wang等[6]通过加入期权契约可实现供应链协调,并得出期权价格和执行价格存在负相关关系;蔡洪文等[7]构建了期权契约与广告投入共担的Stackelberg博弈模型,结果表明可协调零售商为主导者的供应链机制。本文拟引入零售商主导的期权契约以协调供应链系统。但区别于上述文献,本文进一步考虑生产商所提供的增值物流服务对于供应链决策的影响。
基于物流服务价值增值,研究供应链协调的文献已有不少。这种增值物流服务通常可体现为:物流服务质量对于产品货损货差的影响[8-9]、物流服务水平影响市场需求[10-13]等形式。对于物流服务水平影响市场需求的情形,杨春等[10]、刘南等[11]均假定需求为物流服务水平的线性函数,分别研究了确定性需求下TPL与单方客户企业、上下游企业之间的供应链协调问题。吴庆等[12]采用eD乘积式的随机市场需求,研究了TPL与客户之间契约合同的设计,结果表明引入的收入共享与成本共担合同可协调TPL服务提供商的物流服务水平和客户企业的存货量,形成双赢局面。吴庆等[13]在文献[12]的基础上,进一步研究了需求受价格和物流努力水平双重影响下的供应链协调问题。本文参照文献[12]中乘积形式的需求假设。不同的是,本文假定生产商承担物流服务并基于期权契约,研究以生产商和零售商为主体的供应链协调机制。
综上,本文考虑生产商提供物流价值增值服务且其物流服务水平影响到终端市场需求,基于期权契约,研究零售商主导的两级供应链协调问题。
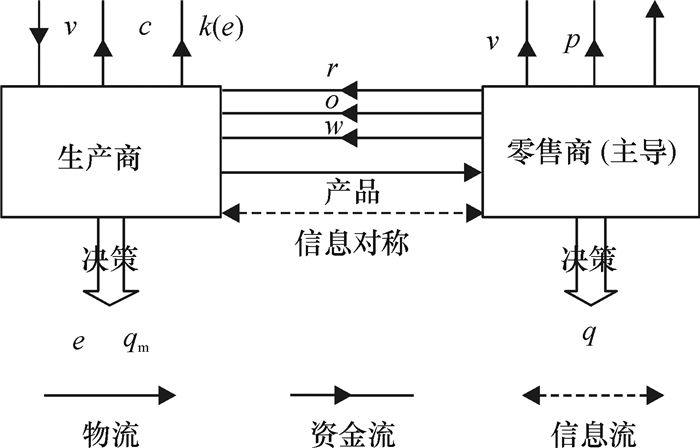
1 问题描述考虑由单生产商和单零售商组成的两级供应链(如图 1所示),零售商为主导者,生产商为跟随者且承担运输任务和费用,将产品直接配送给零售商。在此基础上,研究引入期权契约的供应链协调机制。结合图 1,集中决策模式和分散决策模式运作过程如下。
|
图 1 期权契约下零售商主导的供应链运作模式 Fig. 1 The operation mechanism of retailer-led supply chain under option contract |
集中决策模式下,占据主导地位的零售商依据系统期望利润最大化的原则,使零售商和生产商的利益与供应链整体利益相一致。零售商按w一次性订购q0,以p销售产品,以v处理剩余产品;生产商按c生产产品,以w批发给零售商,并承担物流服务成本k(e)。
分散决策模式下,零售商和生产商依据各自期望利润最大化的原则进行决策。首先,零售商依据掌握的市场信息对产品订购量进行决策,向生产商下订单;其次,生产商依据零售商的订单决策物流服务水平和最大生产量;最后,零售商决策产品订购量。结合图 1,加入期权契约的分散决策模式下,在产品销售期前,零售商通过支付期权价格o,获得第2次订购机会,零售商按w第1次订购产品数量q;销售季节期间,零售商根据市场需求信息变化,按执行价格r第2次订购产品数量,最多订购量为qm-q,以p销售产品,以v处理剩余产品。生产商获得期权价格o,按c生产产品,第1次以w卖出,第2次以r卖出,并承担物流服务成本,若存在剩余产品,以v处理。
1.1 假设条件假设1:生产商与零售商双方信息完全对称。
假设2:生产商与零售商均理性,且是风险中性者,追求各自期望利润最大化。
假设3:使用乘积项eD表示产品实际的市场需求。其中,市场需求D为随机变量,其概率密度函数表示为fD(·),概率分布函数表示为FD(·),在[0, +∞)上是连续可微的,其反函数表示为FD-1(x)。
1.2 变量定义p为零售商销售单位产品的零售价格;w为零售商购买单位产品的批发价格;c为生产商生产单位产品的生产成本;v为剩余的单位产品的处理价格;q为零售商的订购量;e为生产商的物流服务水平,e∈[1, +∞);r为零售商第2次购买单位产品的执行价格;o为零售商购买单位产品的期权价格;β为零售商承担物流服务成本的比例,β∈[0, 1];k(e)为生产商承担的物流服务成本,k′(e)>0,k″(e)>0。
上述变量需满足如下条件。
1) p>w>c>v>0。其中p>w能保证零售商有利可图;w>c能保证生产商有利可图;如果c < v,表示生产商处理剩余产品能获得利润,从而生产商会选择大量生产产品,故c>v。
2) v < r < p。其中r < p可激励零售商第2次订购产品;当生产商存在剩余产品时,r>v能保证生产商选择满足零售商第2次订购,而不会独自处理剩余产品。
3) c-v>o≥0。如果o>c-v,生产商会选择大量生产产品,通过处理剩余产品,也能获得一定的利润,故o < c-v,表明生产商受期权价格的限制,将生产一定数量的产品。
2 数学模型 2.1 集中决策模式集中决策模式记为模型(M0),系统总期望利润为
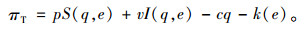
|
(1) |
其中,
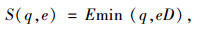
|
(2) |
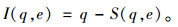
|
(3) |
式(1)中第1项为市场上实际卖出产品所获得的收入,第2项为处理剩余产品获得的收入,第3项为生厂商生产产品的成本,第4项为生产商的物流服务成本。
将零售商的最优订购量记为q0,生产商的最优物流服务水平记为e0,可得命题1。
命题1 模型(M0)存在唯一的最优解(q0, e0),使得系统期望利润最大,且满足:
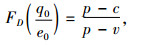
|
(4) |
证明 零售商依据系统总利润最大化的原则,决策产品总订购量q和物流服务水平e。式(1)对q和e分别求一阶偏导数得:
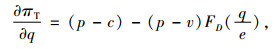
|
(6) |
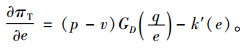
|
(7) |
其中,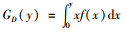
再求模型(M0)的海塞矩阵,可得海塞矩阵
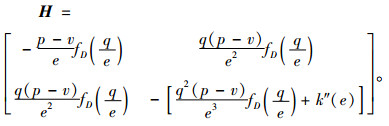
|
由于一阶顺序主子式|H1|=-(p-v)×fD(q/e)/e< 0,二阶顺序主子式|H2|=(p-v)fD(q/e)k″(e)/e>0,故可判定上述海塞矩阵为负定矩阵,进而模型(M0)存在唯一的最优解。令式(6)、(7)等于0,联立方程组,即可求得式(4)、(5)。命题1得证。
2.2 无契约的分散决策模式零售商作为主导者的Stackelberg博弈过程:首先,由生产商根据零售商对市场信息的判断决策物流服务水平,使期望利润最大;随后,零售商决策产品订购量,使自身期望利润最大。决策模型记为(M1)。
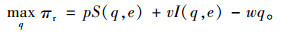
|
(8) |
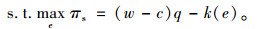
|
(9) |
将分散决策模式下零售商的订购量记为q1,生产商的物流服务水平记为e1,采用逆向归纳法求解式(8)和(9),计算可得:
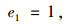
|
(10) |
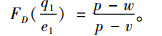
|
(11) |
命题2 零售商主导的两级供应链中,集中决策与分散决策无契约模式下的决策结果和利润满足
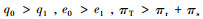
|
证明 1)(M0)和(M1)模型中,最优物流服务水平满足:e1=1 < e0。
2) 比较式(4)和(11),由于w>c和e1=1 < e0,故q1 < q0。
3) 由于q1≠q0,e1≠e0,故系统利润出现损失,πr+πs < πT。命题2得证。
命题2说明,因生产商和零售商均是理性的且具有独立决策权的实体,目标均追求自身利益最大化,双方博弈会导致订购数量和物流服务水平的扭曲,最终系统利润出现损失。因此,需为系统设计合理的契约合同,规避双重边际效应造成的损失。
2.3 分散决策模式下,同时加入期权契约和物流服务成本分担的Stackelberg模型由于单纯的期权契约仅能协调生产商的生产量,故为了激励生产商提高物流服务水平,在期权契约的基础上,进一步加入物流成本分担契约,即由零售商和生产商共同分担物流服务成本。假定零售商的物流服务成本分担比例为β。
加入期权契约和物流服务成本分担契约后,根据第1节中的博弈过程,可构造博弈模型(M2):

|
(12) |
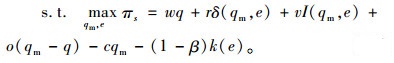
|
(13) |
其中,qm≥q。
式(12)中,第1项为零售商实际卖出产品的收入,第2项为零售商处理剩余产品的收入,第3项为零售商第1次购买产品的成本,第4项为零售商第2次购买产品的成本,第5项为零售商购买期权的成本。式(13)中,第1项为生产商第1次批发给零售商的收入,第2项为生产商第2次批发给零售商的收入,第3项为生产商处理剩余产品的收入,第4项为生产商获得的期权收入,第5项为生产商生产产品的成本,第6项为生产商的物流服务成本。
命题3 加入期权和物流服务成本分担的组合契约,可完美协调零售商主导的两级供应链,系统契约参数需满足:
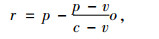
|
(14) |
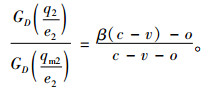
|
(15) |
其中,o/(c-v)≤β≤1。
证明 首先,生产商对生产量和物流服务水平进行决策。式(13)分别对qm和e求一阶偏导得:
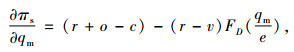
|
(16) |
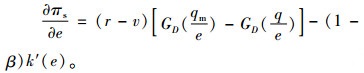
|
(17) |
其中,式(16)需满足:
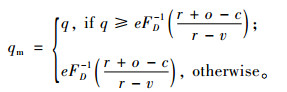
|
根据式(12)和(13),进一步计算其二阶导数,容易证明式(9)海塞矩阵负定的条件为
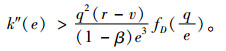
|
(18) |
故此时系统(M2)存在唯一的均衡解,使生产商的期望利润最大。该模式下,将生产商的最优订购量记为qm2,最优物流服务水平记为e2,零售商第1次订购量的最优解记为q2。令式(16)和(17)均等于0,联立方程得:
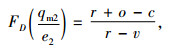
|
(19) |
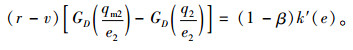
|
(20) |
令qm2=q0,e2=e0代入到式(6)、(7)、(19)和(20),可得式(14)和(15)。
再由式(14)式可知,r < p且r是关于o的表达式,这表明期权价格与执行价格存在负相关关系。根据式(15)可知q2是关于o的表达式,表示只受期权价格影响;当0≤q2≤qm2时,0≤GD(q2/e2)≤GD(qm2/e2),再结合式(15)可得o/(c-v)≤β≤1。命题3得证。
命题3说明,当系统中的契约参数满足特定条件时,可实现供应链的完美协调。进一步可分析零售商的决策过程。由于β不变的前提下,r和q3均用o表示,零售商为使利润最大化,只需制定适合的期权价格。故将式(14)、(15)代入(12),再结合式(16),可得零售商的决策模型(M3)为:
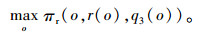
|
(21) |
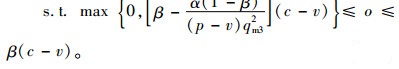
|
(22) |
假定市场需求服从均匀分布,即D~U35, 125,系统参数取值分别为:p=8,w=6,c=5,v=4,α=200。由式(4)和(5)计算可得:qm1=105.703 1,e1=1.031 3,再代入式(1)可得:πT(qm1, e1)=106.347 7。
以下对参数β进行灵敏度分析。β的取值范围为[0, 1],通过改变β,求解非线性规划(M3),即可求得每个β对应的最优期权价格o*。依据式(18)可知:β∈[0, 0.222]时,零售商支付给生产商的期权价格变化范围为[0, β];β∈(0.222, 1]时,期权价格的变化范围为[1.286β-0.286, β]。
从图 2~4中可知,当β∈[0, 1]时,所有的曲线均呈分段式,可知式(22)中,o的两个下限和一个上限导致最优期权价格的转换从边界点到内点,或相反。因此,分成4个区间讨论曲线。
|
图 2 物流成本分担系数与最优期权价格的关系 Fig. 2 Relationship between logistics service cost sharing coefficient and the optimal option price |
|
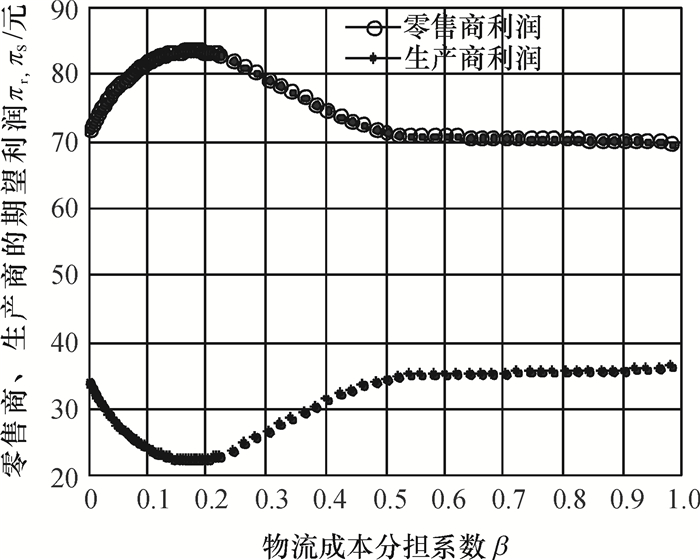
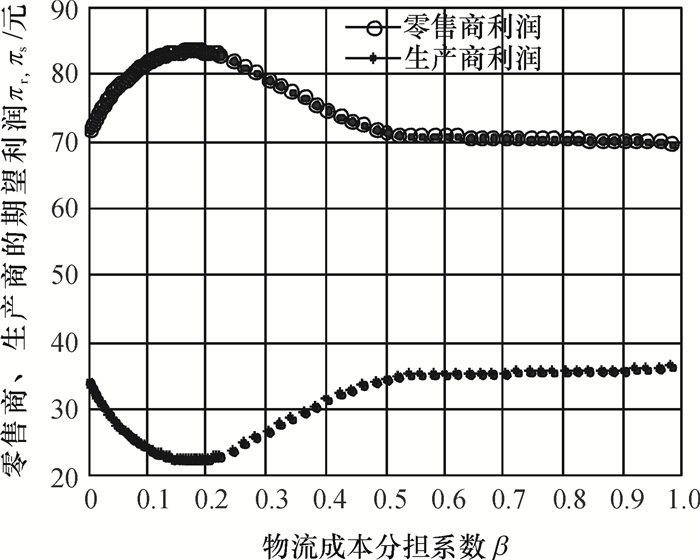
图 3 物流成本分担系数与零售商、生产商期望利润的关系 Fig. 3 Relationship between the logistics service cost sharing coefficient and the expected profit of both sellers and manufacturers |

|
图 4 物流成本分担系数与最优初始订购量的关系 Fig. 4 Relationship between logistics service cost sharing coefficient and the optimal initial ordering quantity |
1) β∈[0, 0.222]区间上,o*=0,q3和β并非线性关系。此外q3急剧增加,达到59.147。随着β的增加,πr*逐渐增加,达到83.183,πs*逐渐减少,最小值为23.164。
2) β∈(0.222, 0.402)时,o*=1.286β-0.286,q3恒为59.147,相比第1区间,随着β的增加,πr*降低而πs*增加。
3) β∈[0.402,0.562)时,o*的取值范围为[1.286β-0.286, β]。随着β的增加,q3急剧下降,最小值为39.096;πr*继续下降,但相比第2区间较平滑,πs*反之。
4) β∈[0.562,1)时,o*=β,q3为36.096。πr*相比第3区间减少变慢。
4 结论本文研究了零售商主导的两级供应链协调机制。通过研究发现加入期权契约和物流服务成本共担契约,可完美协调该供应链,同时零售商的第2次订购价格与期权价格之间存在负相关的关系。通过算例仿真,分析了在市场需求为随机变量且服从均匀分布,物流服务成本为物流服务水平的二次函数的情形下,通过改变物流成本分担系数,零售商支付给生产商的最优期权价格、零售商和生产商的最优期望利润以及零售商最优初始订购量呈现分段形式。未来的研究方向将考虑在该模型中零售商和生产商都存在缺货成本的情形。
| [1] |
HUA Z S, LI S J. Impacts of demand uncertainty on retailer's dominance and manufacturer-retailer supply chain cooperation[J].
International Journal of Management Science, 2008, 36(5): 697-714.
|
| [2] |
LI S J, SHU J, ZHAO L D. Supply chain coordination under uncertainty international handbooks on information systems[C]. Berlin: Springer Berlin Heidelberg Publisher, 2011: 427-454.
|
| [3] |
KLEINDORFER P R, SAAD G H. Managing disruption risks in supply chains[J].
Production and Operations Management, 2005, 14(1): 53-68.
|
| [4] |
LUO M L, LI G, WAN C L JOHNNY, et al. Supply chain coordination with dual procurement sources via real-option contract[J].
Computers & Industry Engineering, 2015, 80: 274-283.
|
| [5] |
CHEN X, HAO G, LI L. Channel coordination with a loss-averse retailer and option contracts[J].
International Journal of Production Economics, 2014, 150: 52-57.
DOI: 10.1016/j.ijpe.2013.12.004. |
| [6] |
WANG X L, LIU L W. Coordination by option contracts in a retailer-led supply chain with demand update[J].
Tsinghua Science & Technology, 2008, 13(4): 570-580.
|
| [7] |
蔡洪文, 蔡洪武, 张殿业. 零售商主导的联合广告投入共担期权契约模型[J].
系统工程学报, 2011, 26(3): 322-329.
CAI Hongwen, CAI Hongwu, ZHANG Dianye. Fuzzy option contract with jointed advertising investment sharing in a retailer-let supply chain[J]. Journal of System Engineering, 2011, 26(3): 322-329. |
| [8] |
尤建新, 劳水琴. 涉及第三方物流服务质量的供应链协调[J].
同济大学学报(自然科学版), 2012, 40(9): 1422-1427.
YOU Jianxin, LAO Shuiqin. Supply chain coordination involving logistics service quality of TPLSP[J]. Journal of Tongji University (Natural Science), 2012, 40(9): 1422-1427. |
| [9] |
赵泉午, 张钦红, 卜祥智. 不对称信息下基于物流服务质量的供应链协调运作研究[J].
同济大学学报(自然科学版), 2008, 22(1): 58-61.
ZHAO Quanwu, ZHANG Qinhong, BU Xiangzhi. Study on supply chain coordination based on logistics service quality with asymmetric information[J]. Journal of Tongji University (Natural Science), 2008, 22(1): 58-61. |
| [10] |
杨春, 但斌, 吴庆, 等. 考虑保鲜努力的生鲜农产品零售商与物流服务商的协调合同[J].
技术经济, 2010, 29(12): 122-126.
YANG Chun, DAN Bin, WU Qing, et al. Coordinating contract between retailer of fresh agricultural product and logistics service provider based on fresh-keeping effort[J]. Technology economics, 2010, 29(12): 122-126. DOI: 10.3969/j.issn.1002-980X.2010.12.023. |
| [11] |
刘南, 吴桥, 鲁其辉, 等. 物流服务商参与时两级供应链的协调策略研究[J].
软科学, 2011, 25(10): 125-129.
LIU Nan, WU Qiao, LU Qihui, et al. Research on coordination strategy of two-level supply chain with the logistic service provider involved[J]. Soft Science, 2011, 25(10): 125-129. DOI: 10.3969/j.issn.1001-8409.2011.10.027. |
| [12] |
吴庆, 但斌. 物流服务水平影响市场需求变化的TPL协调合同[J].
管理科学学报, 2008, 11(5): 64-75.
WU Qing, DAN Bin. Third party logistics coordination contracts with logistics service dependent marked demand[J]. Journal of Management Science in China, 2008, 11(5): 64-75. |
| [13] |
吴庆, 但斌, 钱宇, 等. 努力水平影响损耗的低值易逝品TPL协调合同[J].
管理科学学报, 2014, 17(12): 15-26.
WU Qing, DAN Bin, QIAN Yu, et al. Third party logistics coordinating contracts for low value perishable products with loss dependent on logistics effort levels[J]. Journal of Management Science in China, 2014, 17(12): 15-26. |
 2016, Vol. 19
2016, Vol. 19