生鲜农产品(包括蔬菜、水果、禽、蛋、水产品、肉、奶制品等)是一类高易腐性和短生命周期的产品,对运输环节的要求相当苛刻,但我国冷链物流发展滞后加之由于运输过程中的不确定因素(包括不利天气、交通堵塞等)所引起的运输时间的延长,生鲜农产品到达销售市场的有效供给量和新鲜度很难达到市场需求。据相关资料统计,我国生鲜农产品损耗严重,果蔬、肉类、水产品的流通损耗率分别达到20%~30%、12%、15%,仅水果蔬菜每年损失就达到1 000亿元以上,而发达国家的损耗率低于5%[1]。
目前,国内外学者对易变质产品在流通过程的损耗控制问题给予了高度的关注。Lee等[2]在假设库存影响需求的条件下构建变质库存模型,得出了零售商的最优保鲜技术成本和最佳补货时间。Dye等[3]建立了变质率随时间变化和部分产品短缺的生鲜农产品库存模型,并以单位时间利润最大化为目标,得出了零售商的最佳补货计划和最优保鲜技术投入成本。Ahumada等[4]考虑由于天气和需求的变化导致生鲜农产品在生产和配送过程中的不确定性,提出了一种随机战略规划模型来生产和销售生鲜农产品。Hsu等[5]假设零售商通过投入保鲜技术来降低生鲜农产品的变质率,提出了一种方案, 得出了零售商的最优订货周期、订货数量、短缺时间以及保鲜技术成本来使零售商的单位时间总利润最大化。此外,针对生鲜农产品昂贵的冷链运输费用和较大的保鲜技术难度,诸多国内外学者开始探讨如何加强生鲜农产品供应链节点企业的合作,实现生鲜农产品供应链的协调。Cai等[6]假设分销商对生鲜农产品进行保鲜并且保鲜努力水平会同时影响生鲜农产品的质量和数量,在此基础上研究了生鲜农产品供应链的协调问题。Su等[7]在假设生鲜农产品的供给和需求随机的前提下,通过构建考虑运输时间的生鲜农产品供应链模型,得出了最优订购量和最优运输时间,并通过风险分担契约实现了供应链的协调。肖勇波等[8]考虑生产商运输生鲜农产品到远距离批发市场的过程中面临的延误和产品衰减风险,设计了一种简单的成本分担契约来实现生鲜农产品供应链的协调。
事实上,供应链中的成员并不总是完全理性的,不总以利润最大化作为自身的决策准则,大量博弈实验证据表明,人们的公平偏好是普遍、客观存在的,公平偏好对社会经济活动具有广泛的影响[9]。Cui等[10]将公平偏好引入到二级供应链中,研究了公平偏好对供应链契约协调的影响。Caliskan等[11]拓展了Cui的模型,研究了非线性需求下考虑公平偏好的供应链协调,表明当只有零售商具有公平偏好行为倾向时,相对于线性需求函数,指数需求函数达到协调所需要的条件相对宽松。Ho等[12]在由一个供应商和两个零售商组成的二级供应链中,研究了零售商同时存在横向和纵向公平偏好时的契约设计问题。Ellingsen等[13]在由一个代理方和一个卖方组成的二级供应链中考虑卖方的公平偏好,研究了公平偏好对双边交易的影响。
通过文献回顾发现,已有关于生鲜农产品供应链的研究鲜有将供应链成员的公平偏好纳入研究视角,这往往不符合现实情况。因为在生鲜农产品供应链中,利益的不均衡会促使供应链成员关注分配的公平性,甚至作出投机行为。例如,下游销售商往往获取供应链较多的利润,便会使得上游生产商产生不公平感而采取添加三聚氰胺、瘦肉精等危害健康的行为,这种通过牺牲自身利益达到惩罚对方目的的做法势必会导致“两败俱伤”,损害供应链的整体利益。因此,在生鲜农产品供应链中考虑生产商的公平偏好,解决如何将不确定的供给和市场需求相匹配及提高各自利润的难题具有重要的现实意义。鉴于此,本文针对由于生鲜农产品的易变质特征以及运输过程中的不确定性因素所引起的有效供给和变质的随机性,充分考虑生产商的公平偏好并分析其对生鲜农产品供应链的运作产生的影响,拟设计一种协调机制来协调具有公平偏好的生鲜农产品供应链,同时实现双方决策目标的Pareto改进。
1 模型描述与假设研究由一个生产商和一个销售商组成的二级生鲜农产品供应链系统,生产商供应边际生产成本cm的单品种生鲜农产品,考虑单周期模型。在销售季节来临前,销售商依据生产商制定的批发价格ω向生产商订购q单位的生鲜农产品,同时借助运输工具将生鲜农产品以边际运输成本ct运到远距离的销售市场,运输过程中发生的费用和风险由销售商自行承担。由于生鲜农产品是一类高易腐性的产品,难免会由于运输时间的延长发生损耗,假设产品刚被装上车辆时完全新鲜,且具有一定的保鲜期τ(τ≥0),τ的大小取决于产品的特性以及包装方式,一旦超过保鲜期,生鲜农产品开始变质,发生实体损耗(有效数量的减小)和价值损耗(新鲜度的降低),到达销售市场之后,销售商根据生鲜农产品的损耗状态和市场需求确定合适的销售价格p。为了有效刻画由于运输的不确定性所引起的生鲜农产品的损耗以及其他相关信息,本文作出如下具体假设。
1) 由于在运输途中可能会遭遇不利天气和交通堵塞,生鲜农产品运送至销售市场的时间T是不确定的,假设T是区间[A, B]上的连续型随机变量,累积分布函数(CDF)和概率密度函数(PDF)分别为G(t)和g(t)。
2) 运输时间越长,生鲜农产品越不新鲜,表现为表面蒙尘和水分缺失等,记新鲜度因子θ(t)∈[0, 1],当t∈(0, τ]时,θ(t)=1;当t∈(τ, B]时,θ(t)∈[0, 1),且满足θ′(t) < 0, θ″(t) < 0。
3) 运输时间越长,生鲜农产品会由于损坏而引起数量减少,记与运输时间相关的有效供给率m(t)∈[0, 1],当t∈[0, τ]时,m(t)=1;当t∈(τ, B]时,m(t)∈[0, 1),且满足m′(t) < 0, m″(t) < 0。因此,当销售商订购q单位的生鲜农产品时,经过运输时间t,到达销售市场的有效数量将变为qm(t)。
4) 生鲜农产品的市场需求取决于t时刻达到销售市场的新鲜度θ(t)以及销售商确定的销售价格p,采用乘积形式的市场需求函数为d(p, t, ε)=ap-kθ(t)ε, k>1,其中a是对市场需求规模的一个度量,k是市场需求对销售价格的弹性系数,ε是均值为1的连续分布随机因子,累积分布函数(CDF)和概率密度函数(PDF)分别为F(x)和f(x)。
5) 生产商和销售商信息完全对称,风险中性,剩余产品的残值为0,不考虑缺货造成的损失。
以πm、πr、πsc以及um分别表示生产商和销售商的利润、供应链系统利润以及生产商的效用,上标c、n、d、f以及N分别表示集中决策、生产商公平中性和具有公平偏好时的分散决策、组合式契约以及相应的非易腐品供应链情形,上标*代表最优。
2 生鲜农产品供应链的基准决策模型 2.1 集中决策模型在集中决策下,生产商和销售商根据生鲜农产品的市场随机需求从供应链整体期望利润最大化角度出发确定最优的订购量和销售价格。供应链系统的期望利润函数(以下简称利润函数)为
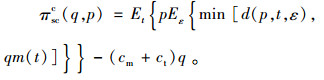
|
(1) |
借鉴Petruzzi等[14]的做法,定义“库存因子”z=qm(t)/[ap-kθ(t)],那么供应链系统的利润函数可转化为
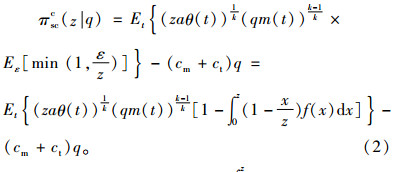
|
(2) |
最优库存因子z0由方程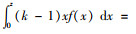
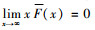
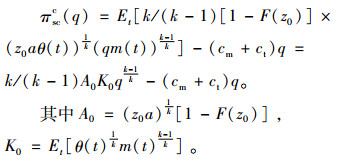
|
(3) |
其中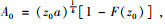
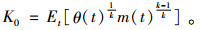
|
不难验证供应链系统的利润函数为订购量q的严格凹函数,因此可以求得集中决策下的最优订购量、最优销售价格以及供应链系统的最优利润分别为

|
(4) |
在分散决策下,生产商和销售商是一个Stackelberg博弈过程,由逆向归纳法可知,在博弈第2阶段销售商依据批发价格ω从自身利润最大化的角度出发确定最优的订购量和销售价格,销售商的利润函数
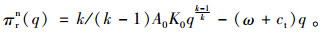
|
(5) |
令(πrnq)关于订购量q的一阶导数等于0可得销售商的最优订购量和销售价格分别为:
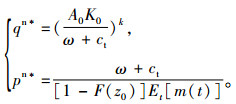
|
(6) |
在博弈第1阶段,生产商从自身利润最大化角度出发制定最优的批发价格,生产商的决策问题为
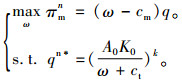
|
(7) |
求解上式可得生产商的最优批发价格并代入式(6)可得:
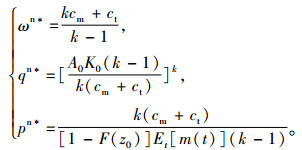
|
(8) |
由式(8)可知生产商、销售商以及供应链系统的最优利润分别为:
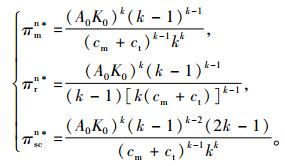
|
(9) |
对于具有公平偏好的生产商而言,不仅关注自身的利润同时还关注渠道公平,本文借鉴Fehr等[15]和Cui等[10]的定义将生产商的效用函数定义如下:
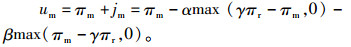
|
(10) |
其中jm表示生产商的公平负效用,α和β分别表示生产商的不公平规避系数和同情心理系数,且0≤β<α,0 < β < 1,γ是生产商的公平感知系数,反映了其在渠道中的力量强弱,且γ>0。若生产商的利润低于销售商利润的γ倍,会产生α倍利润差的嫉妒负效用;若生产商的利润高于销售商利润的γ倍,会产生β倍利润差的同情负效用。由于生产商更多关注由于自身利润小于销售商利润的γ倍而产生的嫉妒负效用,因此下文仅考虑πm≤γπr的情形。
同理,由逆向归纳法可知,在博弈第2阶段销售商作决策,求解结果同式(6),在博弈第1阶段,生产商从自身效用最大化角度出发制定最优的批发价格,在满足γπr≥πm时,生产商的决策问题可以描述为:
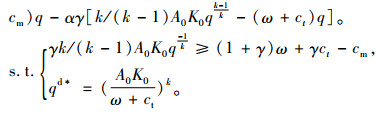
|
(11) |
用K-T条件求解上述问题,可得以下2种情况。
情况1 当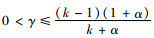
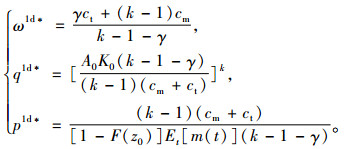
|
(12) |
由式(12)可知,生产商的最优利润和效用、销售商的最优利润以及供应链系统的最优利润分别为:
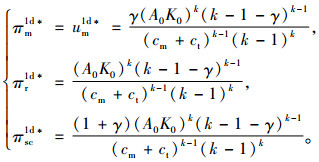
|
(13) |
情况2 当
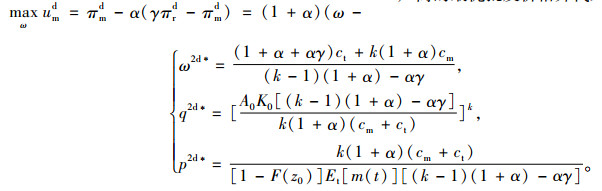
|
(14) |
由式(14)可知,生产商的最优利润和效用、销售商的最优利润以及供应链系统的最优利润分别为

|
(15) |
分析情况1和情况2,并将求解结果与公平中性、集中决策情形进行对比可得如下结论。
定理1 存在公平感知系数阈值γ1=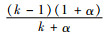
证明
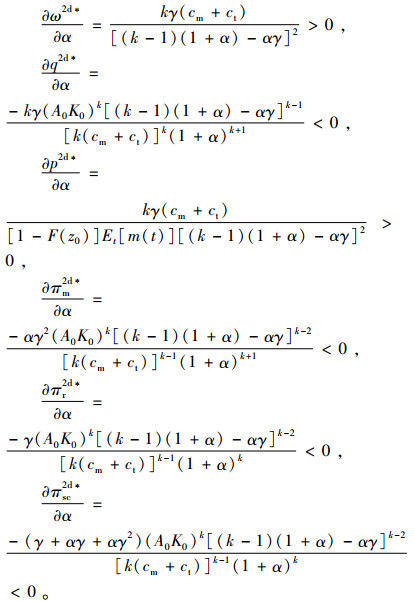
|
证毕。
由定理1可知,在同样的不公平规避系数下,生产商的公平感知系数越小,越不容易产生嫉妒负效用。公平感知系数越大,生产商产生的嫉妒负效用会加剧双重边际效应,对双方均会造成不利影响。此外,观察γ1的表达式可知,阈值γ1的大小与生产商的不公平规避系数正相关,即生产商的不公平感越强,使其产生嫉妒负效用的公平感知系数的取值区间越小。
定理2
1)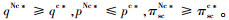
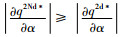
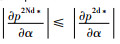
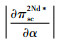
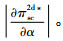
证明 若产品是非易腐性的,则有θ(t)≡1,m(t)≡1,即K0≡1,而若产品是易腐性的,则有θ(t)≤1,m(t)≤1,即K0≤1。结合上述求解结果可得如上结论。证毕。
由定理2可知,不管在集中决策还是在生产商公平中性和具有公平偏好时的分散决策下,与相应的非易腐品供应链相比,生鲜农产品供应链的订购量和系统利润偏低,销售价格偏高,而分散决策时的批发价格相等。此外,在生产商产生嫉妒负效用时,生鲜农产品供应链的订购量和系统利润对生产商不公平规避系数的敏感程度以及相对于公平中性时的降低量比相应的非易腐品供应链低,而生鲜农产品供应链的销售价格对生产商不公平规避系数的敏感程度以及相对于公平中性时的增加值比相应的非易腐品供应链高。
定理3 存在公平感知系数阈值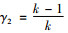
证明 当0 < γ≤γ2时,ωd*=ω1d*,qd*=q1d*,pd*=p1d*,πmd*=πm1d*,πnd*=πn1d*,πscd*=πsc1d*。
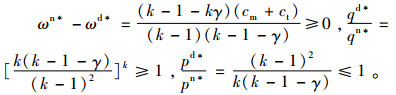
|
令g(γ)=πrd*-πrn*,易知γ2为g(γ)的零点,而g′(γ)≤0,即g(γ)≥g(γ2)=0,同理可知πmd*≤πmn*,πscn*≤πscd*;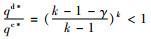
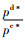
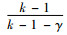
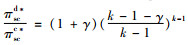
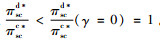
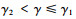
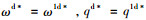
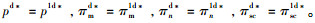
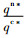
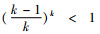
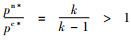
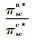
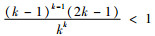
由定理3可知,当生产商的公平感知系数介于0~γ2时,生产商的批发价格和销售商的销售价格均低于公平中性时的情形,而销售商的订购量和利润以及供应链系统利润均高于公平中性时的情形,即此时生产商的公平偏好减轻了双重边际效应;当生产商的公平感知系数大于γ2时,生产商的批发价格和销售商的销售价格均高于公平中性时的情形,而销售商的订购量和利润以及供应链系统利润均低于公平中性时的情形,即此时生产商的公平偏好加剧了双重边际效应。此外,不管生产商的公平感知系数如何选取,生产商的利润均小于公平中性时的情形,而供应链的最优决策和系统利润均未达到集中决策水平,即生产商的公平偏好对自身始终是不利的,也无法实现生鲜农产品供应链的协调,因此需设计相应的协调机制解决公平偏好下生鲜农产品供应链最优决策的扭曲问题。
3 基于“风险分担+收益共享”的协调机制由定理3的分析可知,尽管在分散决策下生产商的公平偏好可能会减轻双重边际效应,但销售商的订购量和销售价格还是偏离了集中决策水平,因此要想实现生鲜农产品供应链的协调,需使得销售商的最优决策达到集中决策水平。由于生鲜农产品的易变质会引起销售商在运输以及销售过程中的不确定性,使得在分散决策下销售商独自承担了运输和销售“双重风险”,生产商为激励销售商提高订购量,需设计分担销售商面临风险的协调机制:一方面需要通过批发价格折扣来分担销售商的运输风险,另一方面需要给予销售商未售出的单位生鲜农产品一定的补偿。但生产商具有不公平感,一味地让生产商分担销售商面临的风险显然不符合现实情况,因此销售商在生产商风险分担的基础上,需将销售收入的ξ(0 < ξ < 1)份额共享给生产商,该支付也可以看作是防范销售商的道德风险的保证金。这里假设生产商给出的批发价格为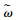
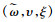
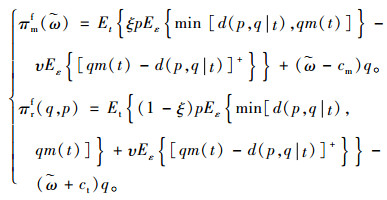
|
(16) |
定理4 在考虑生产商公平偏好的情形下,若设计的协调机制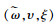
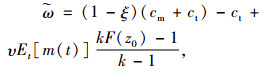
|
(17) |
则qf*=qc*,pf*=pc*,πmf(qf*, pf*)+πrf(qf*, pf*)=πscc(qc*, pc*)。
证明 在协调机制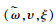
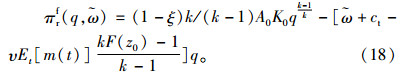
|
(18) |
同理可得组合式契约下的最优决策为:
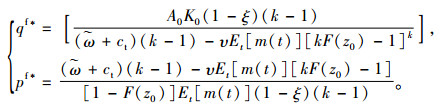
|
(19) |
将式(17)代入式(19)可得qf*=qc*,pf*=pc*,从而πmf(qf*, pf*)+πrf(qf*, pf*)=πscc(qc*, pc*)。证毕。
由定理4可知,当生产商的批发价格、单位生鲜农产品的补偿以及销售商的收益共享份额满足一定的条件下可使销售商选择集中决策时的最优解,即实现了生鲜农产品供应链的完美协调。此外,由式(17)可知生产商的协调批发价格与销售商的有效供给率有关,进一步分析可得如下推论。
推论1 1)生产商的协调批发价格与销售商的有效供给率正相关。
2) 若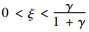
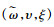
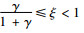
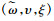
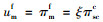
证明 由定理4可知,在协调机制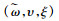
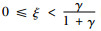
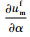
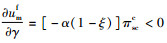
由推论1的1)可知,生产商通过将批发价格与销售商的有效供给率相关联能够有效分担销售商由于生鲜农产品的变质而引起的运输风险,即生鲜农产品的损耗比例越大,生产商给予的批发价格折扣就越多。由2)可知,存在收益共享份额阈值,使得当销售商的收益共享份额低于该阈值时,生产商在协调机制下仍具有公平偏好,并且生产商的公平偏好会降低自身效用,但不管销售商的收益共享份额如何选取,双方的利润均不受生产商公平偏好的影响;当销售商的收益共享份额高于该阈值时,此时协调机制能够消除生产商的公平偏好。此外,销售商的收益共享份额ξ并不是任意取值的,若ξ的取值过大,销售商将会失去参与契约的动力,因此为了使得契约有效,还必须在协调后实现双方决策目标的Pareto改进,结合2.3节的情况1和情况2可得如下结论。
定理5 若要使得基于“风险分担+收益共享”的协调机制有效,销售商的收益共享份额ξ还需满足以下条件。
情况1 当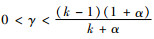
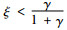
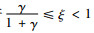
情况2 当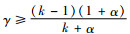
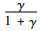
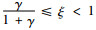
其中
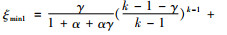
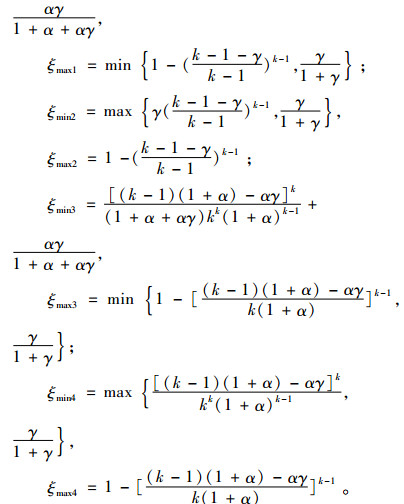
|
证明 要想使得契约有效,生产商的效用以及销售商的利润应该不小于协调前的最优值,即umf(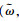
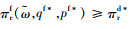
为了验证本文的主要结论,下面通过具体算例分析生产商的公平偏好对分散决策模式供应链的影响,以及“风险分担+收益共享”契约参数对协调效果的影响。基本参数和随机变量设置如下:cm=1.0,ct=0.6,k=2.5,τ=3,a=10 000,z0=4/(k+1),F(z0)=2/(k+1),T~U[1, 5],ε~U[0, 2]。假设生鲜农产品的新鲜度和有效供给率随时间变化的函数分别为:θ(t)=e-σ(t-τ), t∈(3, 5],其中σ表示新鲜度的衰减指数,σ=0.2; m(t)=e-δ(t-τ), t∈(3, 5],其中δ表示有效供给率的衰减指数,δ=0.1。依据参数的取值可得集中决策下的最优订购量、销售价格以及供应链系统利润分别为299.05、4.13和318.99。
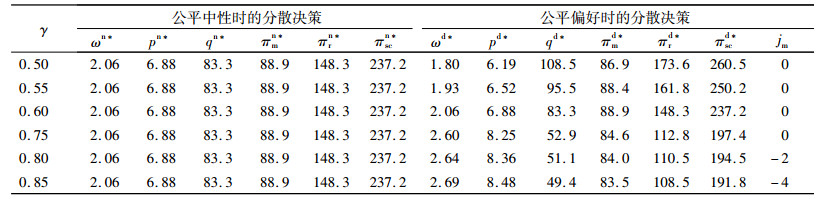
4.1 生产商公平偏好对双方最优决策和利润的影响首先取α=0.50,分析生产商的公平感知系数γ对分散决策模式供应链的影响,如表 1;其次取γ=0.85,分析在生产商产生嫉妒负效用时,不公平规避系数α对分散决策模式供应链的影响,如表 2;最后取γ=0.85,对比分析在τ=3和τ=5时生产商的不公平规避系数对生鲜农产品供应链最优决策和利润的影响,如表 3。
| 表 1 生产商的公平感知系数对双方最优决策和利润的影响 Tab. 1 Impacts of manufacturer's fairness perception coefficient on both sides' optimal decisions and profits |
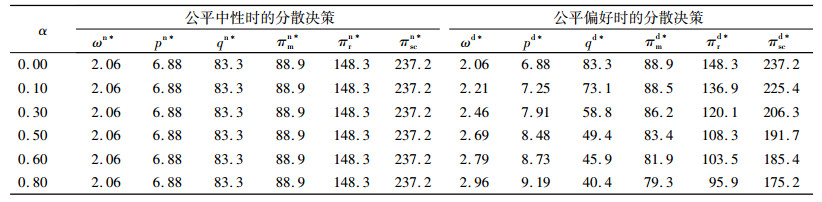
| 表 2 生产商的不公平规避系数对双方最优决策和利润的影响 Tab. 2 Impacts of manufacturer's unfairness aversion coefficient on both sides' optimal decisions and profits |
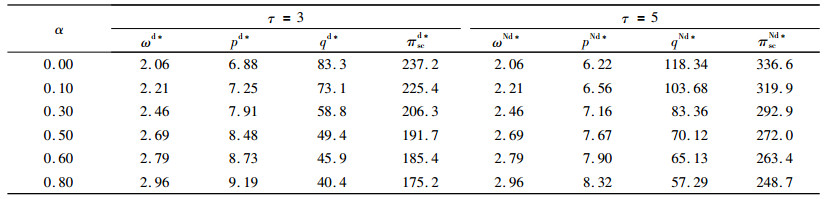
| 表 3 不同保鲜期和不公平规避系数下双方的最优决策和利润 Tab. 3 oth sides' optimal decisions and profits on different freshness-keeping period and unfairness aversion |
从表 1可以发现,当生产商的公平感知系数γ < 0.80时,生产商的嫉妒负效用均为0;当γ>0.80时,生产商产生嫉妒负效用,进一步验证了定理1的结论。当生产商的公平感知系数γ < 0.60时,生产商具有公平偏好时的批发价格和销售价格均低于公平中性情形,而销售商的订购量和利润以及供应链系统利润均高于公平中性情形,即此时生产商的公平偏好减轻了双重边际效应;当γ>0.60时,会得出相反的结论,并且不管生产商的公平感知系数如何变化,生产商的利润均低于公平中性情形,进一步验证了定理3的结论。此外,由表 1还可以发现,生产商具有公平偏好时的批发价格和销售价格均随着公平感知系数的增大而增大,订购量以及供应链系统利润均随着公平感知系数的增大而减小,即生产商的公平感知系数的取值越大,对供应链系统越为不利。
从表 2可以发现,供应链系统的批发价格和销售价格均随着生产商不公平规避系数的增大而增大,而订购量以及供应链系统利润均随着生产商不公平规避系数的增大而减小,进一步验证了定理1的结论。
从表 3可以发现,在τ=5时,有θ(t)=m(t)=1,此时生鲜农产品供应链变为非易腐品供应链,τ=5时的批发价格与τ=3时的批发价格相等,而τ=5时的销售价格低于τ=3时的销售价格,τ=5时的订购量高于τ=3时的订购量,τ=5时的供应链系统利润高于τ=3时的供应链系统利润。仔细观察还可以发现,在生产商的不公平规避系数由0.00增加到0.80时,τ=5时的销售价格提高了2.10,小于τ=3时增加的2.31;τ=5时的订购量降低了61.05,高于τ=3时降低的42.90;τ=5时的供应链系统利润降低了87.90高于τ=3时降低的62.00,进一步验证了定理2的结论。
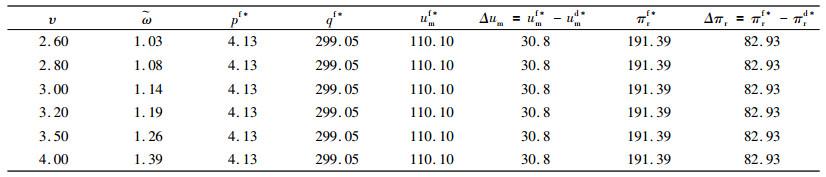
4.2 “风险分担+收益共享”契约参数对协调效果的影响以情况2为例进行算例分析,令α=0.5,γ=0.85。首先取v=4.5,分析销售商的收益共享份额ξ对协调效果的影响,如表 4。其次取ξ=0.40,分析生产商单位生鲜农产品的补偿v对协调效果的影响,如表 5。情况1的算例分析与情况2类似。
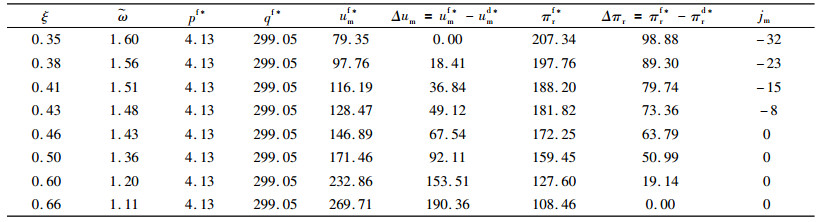
| 表 4 不同收益共享份额下双方最优决策、利润以及效用 Tab. 4 Both sides' optimal decisions, profits and utilities on different share of revenue-sharing |
| 表 5 不同风险补偿下双方最优决策、利润以及效用 Tab. 5 Both sides' optimal decisions, profits and utility on different risk compensation |
从表 4和表 5可以发现,在“风险分担+收益共享”的协调机制下,供应链系统的最优销售价格为4.13,最优订购量为299.05,均等于集中决策情形,而生产商的最优效用和零售商的最优利润均高于分散决策下生产商具有公平偏好情形,即组合式契约实现了生产商公平偏好下生鲜农产品供应链的完美共赢协调。
分析表 4可知,在生产商单位生鲜农产品的风险补偿一定(v=4.5)时,存在一个合理的收益共享份额区间ξ∈[0.35, 0.66]使得双方均可实现决策目标的Pareto改进。另外,随着销售商的收益共享份额的增大,生产商的协调批发价格会降低,这是因为销售商的收益共享份额越大,生产商就会获得更多供应链系统的利润份额,因此会通过降低批发价格来分担销售商面临的运输风险。此外,生产商所增加的效用也会随着销售商的收益共享份额的增大而增大,但销售商所增加的利润会随着自身收益共享份额的增大而减小。由表 4还可发现,在ξ∈[0.35, 0.43)时,组合式契约下生产商仍产生嫉妒负效用,且嫉妒负效用随着收益共享份额的增大而增大,在ξ∈[0.46, 0.66]时,组合式契约下生产商的嫉妒负效用为0,这与推论1的论证相一致。
分析表 5可知,在销售商的收益共享份额一定(ξ=0.40)时,生产商所增加的效用以及销售商所增加的利润均不随单位产品的风险补偿的变化而变化,而生产商的协调批发价格随着单位产品的风险补偿的增大而增大,这是因为生产商单位产品的风险补偿越大,便会选择提高协调批发价格来使自身的利润不受影响,这也说明了生产商单位产品的风险补偿并不会影响协调后双方的利润,只会影响生产商的协调批发价格。
5 结语本文以单一生产商和单一销售商组成的二级生鲜农产品供应链为研究对象,针对生鲜农产品由于易变质特征以及运输过程中的不确定性因素所引起的有效供给和变质的随机性,在充分考虑生产商公平偏好的基础上,首先构建了生产商和销售商间的Stackelberg博弈模型,讨论了生产商的公平感知系数和不公平规避系数取值的变化对生鲜农产品供应链的运作产生的影响,结果发现生产商的公平感知系数存在第1个阈值,当公平感知系数高于(低于)该阈值时,生产商产生(不产生)嫉妒负效用,且第1个阈值的大小与生产商不公平规避系数正相关;生鲜农产品供应链的订购量、销售价格以及系统利润对生产商公平偏好的敏感程度与相应的非易腐品供应链不同;生产商的公平感知系数存在第2个阈值,当公平感知系数高于(低于)该阈值时,生产商的公平偏好会加剧(减轻)双重边际效应。其次以集中决策作为标杆,设计了基于“风险分担+收益共享”的组合式契约作为供应链的协调机制。最后通过数值算例验证了本文的主要结论。
但本文只是考虑了生产商的公平偏好特征,却没有考虑面临运输和销售风险的销售商的风险规避特征,因此未来可以拓展研究由公平偏好的生产商和风险规避的销售商组成的二级生鲜农产品供应链的决策以及协调机制设计问题。
| [1] |
雷露, 乔忠. 生鲜农产品物流损耗控制的障碍与解决对策研究[J].
中国商贸, 2012(30): 134-135.
LEI Lu, QIAO Zhong. Research on the obstacles and solutions of logistics loss control of fresh agricultural products[J]. Chinese Commerce and Trade, 2012(30): 134-135. DOI: 10.3969/j.issn.1005-5800.2012.30.067. |
| [2] |
LEE Y P, DYE C Y. An inventory model for deteriorating items under stock-dependent demand and controllable deterioration rate[J].
Computers & Industrial Engineering, 2012, 63(2): 474-482.
|
| [3] |
DYE C Y, HSIEH T P. An optimal replenishment policy for deteriorating items with effective investment in preservation technology[J].
European Journal of Operational Research, 2012, 218(1): 106-112.
DOI: 10.1016/j.ejor.2011.10.016. |
| [4] |
AHUMADA O, VILLALOBOS J R, MASON A N. Tactical planning of the production and distribution of fresh agricultural products under uncertainty[J].
Agricultural Systems, 2012, 112(13): 17-26.
|
| [5] |
HSU P H, WEE H M, TENG H M. Preservation technology investment for deteriorating inventory[J].
International Journal of Production Economics, 2010, 124(2): 388-394.
DOI: 10.1016/j.ijpe.2009.11.034. |
| [6] |
CAI X, CHEN J, XIAO Y, et al. Optimization and coordination of fresh product supply chains with freshness-keeping effort[J].
Production and Operations Management, 2010, 19(3): 261-278.
|
| [7] |
SU Juning, WU Jiebing, LIU Chenguang. Research on coordination of fresh produce supply chain in big market sales environment[J/OL]. (2014-02-09). [http://dx.doi.org/10.1155/2014/873980.]
|
| [8] |
肖勇波, 陈剑, 徐小林. 到岸价格商务模式下涉及远距离运输的时鲜产品供应链协调[J].
系统工程理论与实践, 2008, 28(2): 19-25.
XIAO Yongbo, CHEN Jian, XU Xiaolin. Fresh product supply chain coordination under CIF business model with long distance transportation[J]. Systems Engineering: Theory & Practice, 2008, 28(2): 19-25. |
| [9] |
浦徐进, 诸葛瑞杰, 范旺达. 考虑横向和纵向公平的双渠道供应链均衡策略[J].
系统工程学报, 2014, 29(4): 527-536.
PU Xujin, ZHUGE Ruijie, FAN Wangda. Impact of horizontal fairness and vertical fairness on strategies in dual-channel supply chain[J]. Journal of Systems Engineering, 2014, 29(4): 527-536. |
| [10] |
CUI T H, RAJU J S, ZHANG Z J. Fairness and channel coordination[J].
Management Science, 2007, 53(8): 1303-1314.
DOI: 10.1287/mnsc.1060.0697. |
| [11] |
CALISKAN-DEMIRAG O, CHEN Y H, LI J B. Channel coordination under fairness concerns and nonlinear demand[J].
European Journal of Operational Research, 2010, 207(3): 1321-1326.
DOI: 10.1016/j.ejor.2010.07.017. |
| [12] |
HO T, SU X, WU Y. Distributional and peer-induced fairness in supply chain contract design[J].
Production and Operations Management, 2014, 23(2): 161-175.
DOI: 10.1111/poms.2014.23.issue-2. |
| [13] |
ELLINGSEN T, JOHANNESSON M. Sunk costs and fairness in incomplete information bargaining[J].
Games & Economic Behavior, 2005, 50(2): 155-177.
|
| [14] |
PETRUZZI N, DADA M. Pricing and the newsvendor problem[J].
Operations Research, 1999, 47(2): 183-194.
DOI: 10.1287/opre.47.2.183. |
| [15] |
FEHR E, SCHMIDT K M. A theory of fairness, competition and cooperation[J].
Quarterly Journal of Economics, 1999, 114(3): 817-868.
DOI: 10.1162/003355399556151. |
 2016, Vol. 19
2016, Vol. 19