在现实生活中,经济实体具有使自身收益最大化的理性行为,而由不同经济实体组成的闭环供应链往往会使其收益受损。不同决策者对待风险的态度直接影响供应链成员的收益。自Rockfeller等[1]提出条件风险值准则(CVaR)后,因条件风险值(CVaR)度量模型[2-3]在供应链风险的刻画和评价度量等方面具有良好的通用性,而被广泛应用于分析供应链成员的决策行为。于春云等[4]将条件风险值(CVaR)运用到供应链中,提出了条件风险偏爱型和条件风险好恶型的概念, 运用收入共享契约对风险规避程度的供应链进行了优化与协调。近年来,大量学者对CVaR准则下如何用契约实现供应链的协调进行了广泛的研究[5-6]。Chen等[7]研究表明只有供应链成员接受契约才有可能实现协调。Gan等[8]指出收益共享契约与回购契约都不能使供应链协调的条件。郭福利等[9]探讨了供应链收益共享契约的设计问题。以上文献主要集中在单一产品销售的分析,而将条件风险值准则(CVaR)应用于兼有废旧品回收再制造活动的闭环供应链系统。胡新平等[10]设计了一个基于双边道德风险的逆向供应链回收激励契约。施国洪等[11]探讨了损失厌恶供应链应对突变风险的收益共享契约问题。朱传波等[12]在供应突发事件下,通过引入条件风险值(CVaR)刻画了零售商的运营目标,构建了收益共享契约下的供应链订货模型。刘明彦等[13]研究了风险厌恶的消费者前提下制造商的两部定价策略。刘忠轶等[14]研究了运用期权契约来实现风险环境下供应链的协调问题。Hsieh等[15]将CVaR方法用在供应链回购契约中。张新鑫等[16]建立了顾客策略行为下基于回购契约的供应链决策模型,探讨了顾客策略行为、成员风险规避性和供应链回购契约的交互影响。以上研究主要运用收益共享契约[11-12]、两部定价契约[13]、期权契约[14]、回购契约[15-16]实现供应链的协调。只有少数学者将回馈和惩罚契约与CVaR准则相结合。李建斌等[17]研究了以零售商订货量或者产品的实际销售量为目标值的回馈和惩罚契约。在以上契约中,主要集中在对单一产品销售的收益共享环节。而在现实生活中,供应链成员之间的利润分配往往是以产品的销售量和废旧品的回收量为衡量标准。除此之外,社会和政府更为关注环境保护和资源的回收利用。因此,本文采用基于新产品的订货量与废旧产品的实际回收量的回馈与惩罚(orders rebate and penalty-recycles rebate and penalty, ORP-RRP)契约更贴合现实。
综上所述,本文将利用条件风险值(CVaR)准则构建了随机需求下单一风险厌恶型的零售商和单一风险中性的制造商组成的闭环供应链系统,探讨了供应链基于ORP-RRP惩罚契约的优化与协调问题,进而分析了风险因子对最优订货量和废旧品回收价格的影响。
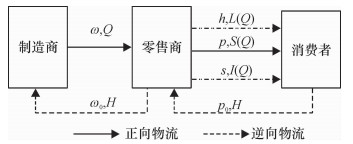
1 模型描述与假设本文考虑一个风险中性的制造商和一个风险厌恶水平为β(0≤β < 1)的零售商组成的两阶闭环供应链(图 1)。在销售季节开始前,制造商以单位成本c制造新产品并根据市场预测以批发价格ω销售给零售商,零售商以零售价格p将产品销售给客户并根据市场预测确定其产品的需求订单为Q,制造商根据订单进行加工生产。销售季节中,零售商的单位缺货损失为h,销售季节结束后,零售商以残值s处理产品。同时,零售商以单位价格p0从废旧品市场中回收有价值的旧产品,并以单位价格ω0销售给制造商回收再制造。假设产品的市场需求x为随机变量,均值为μ,其概率密度函数和分布函数分别为f(x)和F(x)。则期望销售量S(Q)=min(Q, x), 剩余产品数量I(Q)=Q-S(Q), 未满足的期望需求量L(Q)=μ-S(Q)。假设废旧品市场的供给量与产品的销售市场量有关,即废旧产品的回收量H(p0,Q)=τp0Q。根据常理假设:p>ω>ω0>p0>0, ω>c>c0+ω0>p0, c>s>p0, 0≤τ < 1/p0。
|
图 1 再制造闭环供应链系统 Fig. 1 Graphical representation of a closed loop supply chain |
条件风险值准则(CVaR)指在正常的市场条件下和一定的置信水平β上,在给定的时间段内损失的概率超过β的损失的条件期望值[7]。Rockafellar[1]对条件风险值准则(CVaR)提出了更为一般的公式:
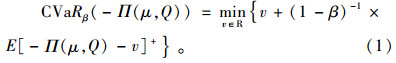
|
(1) |
其中: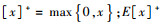
在CVaR准则下的集中式闭环供应链系统决策模型中,集中式闭环供应链系统的期望利润函数为:
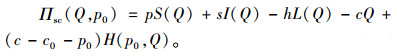
|
(2) |
根据CVaR准则的定义,联合体基于负收益的目标函数为:
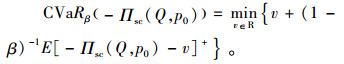
|
(3) |
条件1 当产品销售季节结束时,剩余产品的单位处理残值s需满足:c>s>(c+c0)/2。
定理1 当条件1成立时,基于CVaR的集中式闭环供应链系统的最优生产量(订货量)Q*和最优的旧产品回收价格p0*满足:
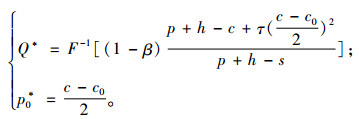
|
证明 根据CVaR准则的定义可知,集中式闭环供应链的决策问题为:
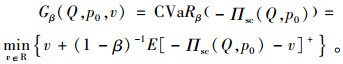
|
(4) |
将集中式闭环供应链的利润函数式(2)代入式(4),得
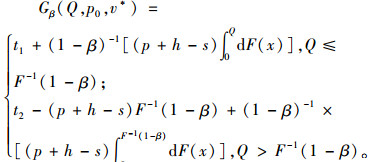
|
式中:t1=(p+h-c)Q-(c-c0-p0)H+hμ,
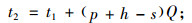
|
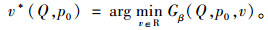
|
分别求Gβ(Q, p0, v*)关于Q和p0的一阶偏导数和二阶偏导数并联立求解即可得,供应链基于CVaR准则的最优生产量(订货量)Q*和最优的旧产品回收价格p0*为:
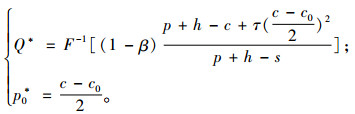
|
根据定理1的证明可知,当Q>F-1(1-β)时,供应链系统无法实现最优化。因此,本文只考虑Q≤F-1(1-β)情况,给定供应链中联合体对风险的规避因子β下的风险值v*(Q, p0)和CVaR条件下联合体的期望负收益函数Gβ(Q, p0, v*)分别为
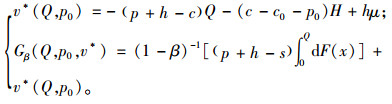
|
(5) |
由式(5)可知,当Q≤F-1(1-β)时,最优生产量Q*随联合体对风险的规避程度β增大而减少,废旧产品的最优回收价格p0*与β无关,CVaR条件下联合体的期望负收益函数Gβ(Q, p0, v*)是关于β的凹函数。制造商为了规避风险,会选择减少产品的生产量。
3 基于CVaR的分散式闭环供应链系统的ORP-RRP契约模型 3.1 零售商基于CVaR准则的均衡决策为了使零售商增加产品的订货量,同时使整个闭环供应链系统达到协调,制造商对产品销售渠道采取基于零售商的预期订货量进行回馈和惩罚ORP,假设回馈和惩罚设定的目标值M, 对超过(低于)目标值的部分每单位产品给予的回馈(惩罚)为k1; 产品回收渠道采取基于零售商的实际回收量进行回馈和惩罚RRP,假设回馈和惩罚设定的目标值N, 对超过(低于)目标值的部分每单位产品给予的回馈(惩罚)为k2。制造商以自身的利润最大化为原则向零售商提供一种基于ORP-RRP契约T(ω*, ω0*, k1, k2, M, N)确定产品的订货量Q和废旧产品的回收价格p0, 且供应链系统成员之间的信息是完全的。
在ORP-RRP契约T(ω*, ω0*, k1, k2, M, N)下,零售商的期望利润函数Πr和制造商的期望利润函数Πm分别为:
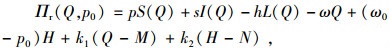
|
(6) |
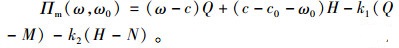
|
(7) |
条件2 新产品的单位回馈或惩罚k1和废旧产品的单位回馈或惩罚需满足:τ(ω0+k2)2/4+k1 < ω-s。
定理2 当条件2成立时,零售商基于CVaR的分散式闭环供应链系统的最优生产量(订货量)Q*和最优的旧产品回收价格p0*满足:
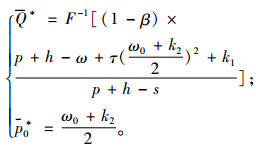
|
证明 同定理1,略。
当Q≤F-1(1-β)时,可得给定零售商对风险的规避因子β下的风险值v*(Q, p0)和基于CVaR条件下联合体的期望负收益函数Gβ(-Πr(Q, p0, v*))为:
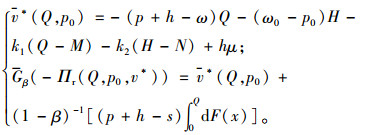
|
(8) |
为了实现闭环供应链的完美协调, 必须使分散决策协调契约的订货量Q*和废旧产品的回收价格P0*分别等于集中决策下的订货量Q*和废旧产品的回收价格p0*,且供应链系统中每个成员在此契约合同下的期望利润不低于每个成员保留的利润。假设制造商和零售商各自保留的利润为纯批发价格和废旧品回收价格下双方的期望利润,分别用πr和πm表示,且πr+πm≤E[Πsc(Q*, p0*)]。
定理3 当基于ORP-RRP契约T(ω*, ω0*, k1, k2, M, N)满足以下条件:1)k1*=ω*-c; 2)k2*=c-c0-ω0*; 3)2s>c+c0; 4)πm≤A=k1*M*+ k2*N*≤E[Πsc(Q, p0*)]-πr时,契约T(ω*, ω0*, k1, k2, M, N)能实现闭环供应链的协调。
证明 根据Gan[8]对考虑条件风险下供应链系统能实现协调的契约必须满足条件并结合本文约束条件,可知基于ORP-RRP契约T(ω*, ω0*, k1, k2, M, N)满足:

|
(9) |
求解式(9)可得:
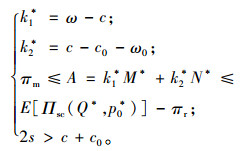
|
即证:当契约满足上述条件时,ORP-RRP契约T(ω*, ω0*, k1, k2, M, N)能实现闭环供应链的协调。
特别地,当M*=N*=0时,即ORP-RRP契约下的变为线性的折扣契约。而此时,零售商获取了整个闭环供应链的期望利润,与现实不符。因此,单纯的线性折扣契约不能使闭环供应链系统实现协调。
4 数值分析假设产品的市场需求x服从均匀分布U(500, 1 000),参数取值分别为:p=15;c=8, c0=2;s=6, h=1;τ=0.1。由前文结论可知,集中决策下产品的最优订货量Q*=945-445β和废旧产品的回收价格p0*=3。此时集中决策下闭环供应链系统的期望负收益为
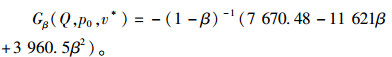
|
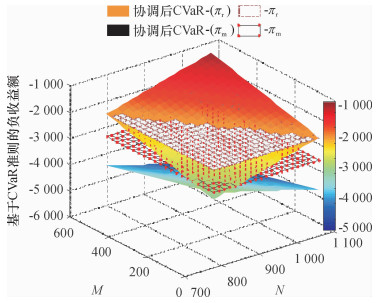
制造商给零售商的纯批发价格契约为T(ω=12, ω0=4)和零售商风险因子β(β=0.3), 则πr=2 080.24, πm=2 816.00, Πsc=6 486.62, A∈[2 816.00, 4 406.38]。图 2进一步分析产品销售和回收的组合回馈(A=k1*M*+k2*N*)对供应链成员之间的相互影响。
|
图 2 ORP-RRP契约协调前后的负收益比较 Fig. 2 The comparison between minus yield before and after ORP-RRP contracts coordination |
从图 2中可以看出,制造商可以通过商议合适的回馈和惩罚契约(k1*=4, k2*=2, A∈[2 816.00, 4 406.38])值能实现基于CVaR准则和风险因子(β=0.3)条件下制造商和零售商之间“双赢”。而且,零售商的CVaRβ(-Πr)随着销售量目标值M*和废旧品的目标值N*增大而增大;制造商的CVaRβ(-Πr)随着销售量目标值M*和废旧品的目标值N*增大而减少;并且当销售量目标值M*和废旧品的目标值N*的组合不能使条件A∈[2 816.00, 4 406.38]成立时,则闭环供应链无法实现协调,因为此时供应链成员中至少有一方的期望利润少于其保留的利润。
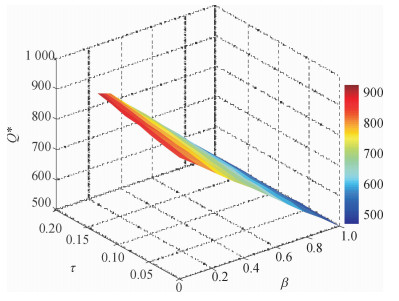
当零售商存在风险厌恶时,图 3给出了风险因子β和再制造品回收敏感性参数τ对零售商最有订货量Q*的影响。从图 3中可以看出,零售商的订货量随着风险因子的增大而减少,随着废旧品的回收敏感性参数的增大而增大,从理论上验证了“零售商为了降低风险而减少订货量”。从零售商的最优订货量
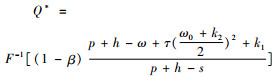
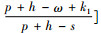
|
图 3 风险因子与再制造产品回收敏感性参数对最优订货量的影响 Fig. 3 The impacts of risk-aversion coefficient and the sensitivity coefficient on optimal ordering quantities |
本文运用条件风险值(CVaR)度量准则建立了基于随机需求下由一个风险厌恶型的零售商和一个风险中性的制造商组成的闭环供应链决策模型,探讨了基于新产品的订货量与废旧产品的实际回收量的回馈与惩罚ORP-RRP契约T(ω*, ω0*, k1, k2, M, N)能否实现闭环供应链的协调问题。并在此基础上,进一步分析了风险因子对最优订货量和废旧品回收价格的影响。本文假设制造商是风险中性的,但现实生活中,当零售商面临风险时,制造商同样会受到风险的影响。例如突发事件影响零售商的订货量,进而影响制造商的生产计划。因此制造商风险厌恶、突发事件和不同时政背景风险等对供应链决策者的决策行为的影响是后续的研究重点。
| [1] |
ROCKAFELLAR R T, URYASEV S. Optimization of conditional value-at-risk[J].
Journal of Risk, 2000, 2(3): 21-42.
DOI: 10.21314/JOR.2000.038. |
| [2] |
ALEXANDER G J, BAPTISTA A M. A comparison of VaR and CVaR constraints on portfolio selection with the mean-variance model[J].
Management Science, 2004, 50(9): 1261-1273.
DOI: 10.1287/mnsc.1040.0201. |
| [3] |
HE X, GONG P. Measuring the coupled risks: a copula-based CVaR model[J].
Journal of Computational & Applied Mathematics, 2009, 223(2): 1066-1080.
|
| [4] |
于春云, 赵希男, 彭艳东, 等. 基于条件风险值理论的供应链优化与协调模型研究[J].
中国管理科学, 2007, 15(3): 31-39.
YU Chunyun, ZHAO Xinan, PENG Yandong, et al. Study of supply chains optimization and coordination model based on conditional value-at-risk[J]. Chinese Journal of Management Science, 2007, 15(3): 31-39. |
| [5] |
高文军, 陈菊红. 基于CVaR的闭环供应链优化与协调决策研究[J].
控制与决策, 2011, 26(4): 489-494.
GAO Wenjun, CHEN Juhong. Research on decisions of closed-loop supply chain optimization and coordination based on CVaR[J]. Control and Decision, 2011, 26(4): 489-494. |
| [6] |
徐兵, 刘露. CVaR准则下双渠道供应链订货与信息搭便车行为[J].
工业工程, 2014, 17(5): 99-107.
XU Bing, LIU Lu. A study of the order and information free-riding behavior of dual-channel supply chain based on CVaR criterion[J]. Industrial Engineering Journal, 2014, 17(5): 99-107. |
| [7] |
CHEN X, SHUM S, SIMCHI-LEVI D. Stable and coordinating contracts for a supply chain with multiple risk-averse suppliers[J].
Production and Operations Management, 2014, 23(3): 379-392.
DOI: 10.1111/poms.12073. |
| [8] |
GAN X, SETHI S P, YAN H. Channel coordination with a risk-neutral supplier and a downside-risk-averse retailer[J].
Production and Operations Management, 2005, 14(1): 80-89.
|
| [9] |
郭福利, 陈菊红. 零售商具有风险规避的供应链收益共享契约设计[J].
工业工程, 2010, 13(2): 6-8.
GUO Fuli, CHEN Juhong. On supply chain revenue sharing contract design with risk-aversion retailer[J]. Industrial Engineering Journal, 2010, 13(2): 6-8. |
| [10] |
胡新平, 王义国. 基于双边道德风险的逆向供应链回收激励契约[J].
工业工程, 2012, 15(3): 24-28.
HU Xinping, WANG Yiguo. Incentive recycling contracts with double moral hazard in reverse supply chain[J]. Industrial Engineering Journal, 2012, 15(3): 24-28. |
| [11] |
施国洪, 曾月凤, 陈敬贤. 损失厌恶供应链应对突变风险的收益[J].
工业工程, 2012, 15(2): 22-26.
SHI Guohong, ZENG Yuefeng, CHEN Jingxian. On revenue sharing contract in loss-aversion supply chain under disruption[J]. Industrial Engineering Journal, 2012, 15(2): 22-26. |
| [12] |
朱传波, 季建华, 曾顺秋. 供应突发事件下基于CVaR的供应链订货决策及协调[J].
管理工程学报, 2015, 29(2): 202-209.
ZHU Chuanbo, JI Jianhua, ZENG Shunqiu. Supply chain ordering decision and coordination mechanism based on CVaR under supply disruption[J]. Journal of Industrial Engineering & Engineering Management, 2015, 29(2): 202-209. |
| [13] |
刘明彦, 齐二石, 刘亮. 基于策略消费者风险偏好的供应链协调研究[J].
工业工程, 2012, 15(2): 27-32.
LIU Mingyan, QI Ershi, LIU Liang. Supply chain coordination with strategic consumer's risk preference considered[J]. Industrial Engineering Journal, 2012, 15(2): 27-32. |
| [14] |
刘忠轶, 陈丽华, 翟昕. 基于期权合约与风险规避型零售商的供应链协调[J].
系统工程, 2013, 31(9): 63-67.
LIU Zhongyi, CHEN Lihua, ZHUO Xi. Supply chain coordination based on option contract and risk-averse retailers[J]. Systems Engineering, 2013, 31(9): 63-67. |
| [15] |
HSIEH C C, LU Y T. Manufacturer's return policy in a two-stage supply chain with two risk-averse retailers and random demand[J].
European Journal of Operational Research, 2010, 207(1): 514-523.
DOI: 10.1016/j.ejor.2010.04.026. |
| [16] |
张新鑫, 侯文华, 申成霖. 顾客策略行为下基于CVaR和回购契约的供应链决策模型[J].
中国管理科学, 2015, 23(2): 80-91.
ZHANG Xinxin, HOU Wenhua, SHEN Chenglin. Decision models for supply chain based on CVaR and buyback contract under strategic consumer behavior[J]. Chinese Journal of Management Science, 2015, 23(2): 80-91. |
| [17] |
李建斌, 余牛, 刘志学. 两种基于CVaR准则的供应链返利与惩罚契约研究[J].
系统工程理论与实践, 2015, 35(7): 1666-1677.
LI Jianbin, YU Niu, LIU Zhixue. Research on two different supply chain rebates and penalty contracts with CVaR criterion[J]. Systems Engineering-Theory&Practice, 2015, 35(7): 1666-1677. DOI: 10.12011/1000-6788(2015)7-1666. |
 2016, Vol. 19
2016, Vol. 19