Clark等[1]提出“级库存”概念以来相继涌现了大量“级库存”优化研究成果。早期文献多数假设供应链各个节点为独立需求条件下的EOQ模型[2-4]。随着经营环境的变化,学者们开始关注不同条件下的EOQ模型研究。Salameh等[5]考虑了一级库存中存在一定残次品的EOQ模型,Wahab等[6]在二级供应链EOQ模型的基础上考虑了残次品和环境的影响,订购量中允许存在一定的残次品,并在运输成本中体现碳排放成本。熊浩[7]研究了最下游节点为独立需求,上游节点需求为与之完全相关需求情景下的供应链多级库存优化问题。Blanchini等[8]探讨了不确定需求下多级库存的成本控制问题;Kim等[9]在随机需求下考虑了3个典型的碳排放许可来源。李兵等[10]在传统EOQ基础上研究了碳单价固定与变动2种情况下的库存管理问题;黄立[11]研究了离散随机需求条件下考虑碳限额和碳单价的最优订货量问题。Hammami等[12]在多级库存中,考虑了碳税和碳限额下的碳排放控制问题。屈晓龙等[13]探讨了模糊条件下碳限额与交易机制下碳排放与碳价对零售商成本的影响;蒋雨珊等[14]基于报童模型,探讨了碳限额与交易机制下最优的生产批量与最优期望利润,并研究了碳限额对订货量、利润与碳排放的影响规律;屈晓龙等[15]研究了二级闭合供应链系统中考虑次品与碳排放对供应链总成本的影响,并研究了碳限额下次品率与碳价对总成本的影响规律。以上成果为供应链多级库存EOQ模型研究奠定了基础。
随着市场竞争的加剧和碳排放限制越来越严格,绿色供应链已然成为未来生产运营组织模式。因此考虑残次品、碳排放的供应链多级库存优化问题逐渐成为供应链管理领域研究的热点之一。本文探究了需求不确定条件下考虑残次品和碳排放供应链多级库存的EOQ模型。
2 问题描述及参数设置 2.1 问题描述以单链多级库存系统为研究对象,结构如图 1所示。图 1表示供应链的n级库存系统结构,圆形表示库存节点,箭头表示各节点间供需关系。

|
图 1 单链多级库存系统 Fig. 1 Single chain multilevel inventory system |
假设节点1订货策略一旦确定,上游节点需求与下游节点需求相关,上游节点采用同步等量订货策略,即上游节点订货周期为其相邻下游节点订货周期的整数倍。每个节点库存中,假设存在残次品率q,且将残次品退回上游供应商。
2.2 前提假设及参数设置 2.2.1 前提假设本文主要研究供应链多级库存的订货策略,即从外部供应商到节点1整条链的订货问题,故目标函数是整条链单位时间总成本最小。因此,假设如下。
假设1 最上游节点n有一个外部供应商,有充足存货满足节点n的订货。
假设2 节点1面临的需求为独立需求,上游节点需求与下游节点需求相关。
假设3 每批货物均允许存在残次品。
假设4 每批货物全部检查。
假设5 货到检查,且检查时间忽略不计,在期末时残次品退回到相应供应商。
假设6 节点1上游节点不允许缺货。
假设7 运输过程中考虑碳排放成本,运输碳排放取决于运输车辆与装载货物量。
假设8 整条供应链使用相同运输车辆。
假设9 正向物流,运输成本由下游节点承担,逆向物流,运输成本由上游供应商承担;即节点i的产品运输时,产生的运输成本及二氧化碳排放成本由节点i-1承担;节点i的残次品退回时,产生的运输成本及二氧化碳排放成本由节点i+1承担。
2.2.2 参数设置本文考虑需求、残次品和碳排放的EOQ模型,参数设置的符号与含义如表 1所示。
| 表 1 参数变量的符号与含义 Tab. 1 Symbols and meanings of parameter variables |
基准模型具体的描述如下。
设D为需求不确定条件下的顾客需求率,且
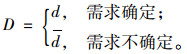
|
设q为残次品率,且

|
设M为碳排放成本,且
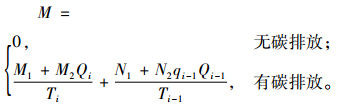
|
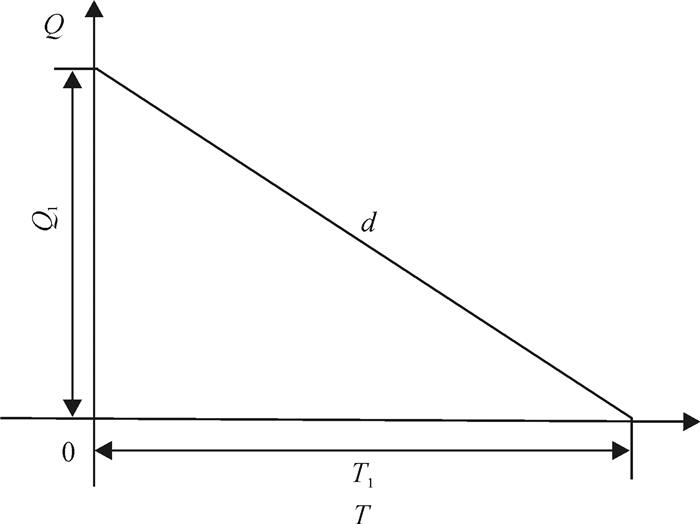
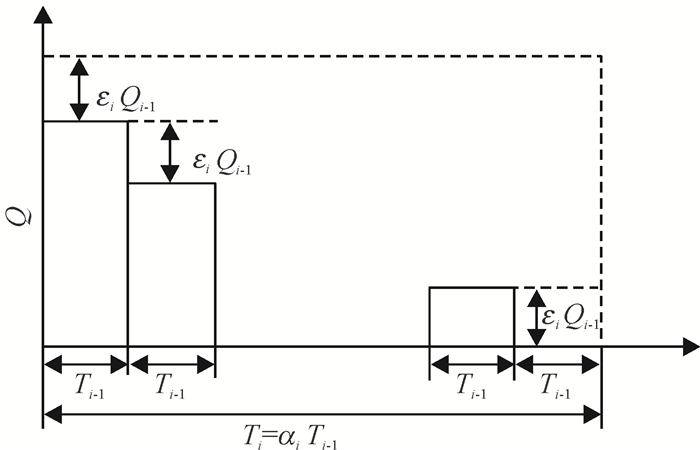
节点1为独立需求,则其在订货周期内的库存为线性,而上游库存处的库存形态为块状,具体如图 2、3所示。
|
图 2 节点1的库存情况 Fig. 2 Inventory of node 1 |
|
图 3 节点i的库存情况 Fig. 3 Inventory of node i |
节点1的单位时间总成本包括4种类型:库存持有成本c11、订购成本c12、运输成本c13和检查成本c14。
根据标准EOQ模型可知,

|
则节点1的总单位时间成本为
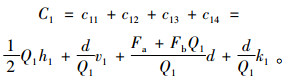
|
(1) |
节点1所有上游节点不允许缺货,节点i单位时间的成本包括:库存持有成本ci1、订购成本ci2、运输成本ci3和检查成本ci4。
由图 3可知,

|
由

|
整理可得:

|
则节点i的总单位时间成本为

|
(2) |
其中,j=2, 3, …, i。
则节点1的所有上游节点的总单位时间成本为

|
(3) |
n为多级库存级数。
所以,多级库存系统的总单位时间成本为

|
(4) |
检查出残次品时,运回到相应的供应商,运费由相应的供应商承担。节点1的实际需求量为T1×d=Q′1(1-q1)=Q1,则Q′1=Q1/(1-q1)为实际订货量。
节点1的单位时间的成本包括4种类型:库存持有成本c′11、订购成本c′12、运输成本c′13和检查成本c′14。

|
则节点1的总单位时间成本为

|
(5) |
节点i的单位时间成本包括:库存持有成本c′i1、订购成本c′i2、运输成本c′i3和检查成本c′i4。则节点i的总单位时间成本为
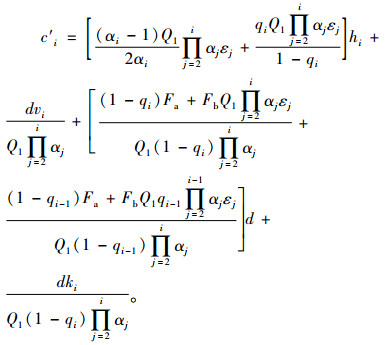
|
(6) |
节点1上游节点总单位时间成本为
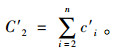
|
(7) |
所以,多级库存系统的总单位时间成本为
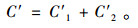
|
(8) |
相比于节点1不允许缺货,存在残次品情况,考虑碳排放影响的成本在运输成本中增加了碳排放成本,即
节点1单位时间的成本包括4种类型:库存持有成本c″11、订购成本c″12、运输成本c″13和检查成本c″14。

|
(9) |
相比于节点1的上游节点不允许缺货,存在残次品,考虑碳排放影响的成本仅仅在运输成本中增加碳排放成本,即
节点1的所有上游节点不允许缺货,节点i的单位时间的成本包括:库存持有成本c″i1、订购成本c″i2、运输成本c″i3和检查成本c″i4。则节点i的总单位时间成本为

|
(10) |
则节点1上游节点的总单位时间成本为
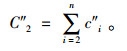
|
(11) |
所以,多级库存系统的总单位时间成本为

|
(12) |
节点1的库存情况如图 4所示。

|
图 4 节点1的库存情况 Fig. 4 Inventory of node 1 |
节点1的单位时间成本包括:

|
则节点1的总单位时间成本为

|
(13) |
节点1缺货最后会传导到顾客,会产生缺货成本,C21的模型与式(3)一致。

|
(14) |
其中,ci如式(2)。
3.2.2 节点1允许缺货,存在残次品节点1单位时间的成本包括4种类型:

|
(15) |
c′i如式(6),节点1上游节点的总单位时间成本C′21以及多级库存的总单位时间成本C′m分别为式(7)和(8)。
3.2.3 节点1允许缺货,存在残次品,考虑碳排放影响相比于节点1允许缺货,存在残次品情况,考虑碳排放影响的成本仅仅在运输成本中增加了碳排放成本,即
节点1所有上游节点不允许缺货,节点1的单位时间的成本

|
(16) |
c″i如式(10),节点1上游节点单位时间成本C″21以及多级库存的单位时间C″m分别为式(11)和(12)。
4 需求不确定条件下的EOQ模型当节点1需求不确定时,只需在节点1处设置安全库存。设多级库存系统的总订货提前期为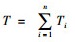

运用(R, Q)策略,当节点1的需求不确定时,其总单位时间成本为
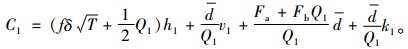
|
(17) |
ci如式(2),节点1上游节点的总单位时间成本C2以及多级库存的总单位时间成本C分别为式(3)和(4)。
ci考虑残次品和碳排放影响的节点1总单位时间成本为

|
(18) |
对于节点1的上游节点订货策略不变,所以之前的模型仍成立。c″i如式(10),节点1上游节点的总单位时间成本C″2以及多级库存的总单位时间成本C″分别为式(11)和(12)。
考虑残次品和碳排放影响的需求不确定的EOQ模型为

|
(19) |
式(19)是一个非线性的混合规划问题,运用精确的算法进行直接的求解很难实现,本文运用LINGO中的非线性进行求解。
5 算例分析 5.1 方法分析利用LINGO工具箱进行处理,Q1, Q0和α2, α3, …αn是整数,通过@gin取整,同时保证α2, α3, …αn大于等于1,求解目标函数中的n个变量Q1和α2, α3, …αn的数值,最终确定整条供应链中单位时间总成本。
5.2 算例描述与结果1) 例1。
考虑一个3级库存系统,节点1的顾客需求率d为120,缺货成本h0=2元固定的运输成本Fa=100元,变动的运输成本Fb=5元,正向物流中,M1=30元,M2=2元,逆向物流中,N1=20元,N2=2元。如表 2所示。
| 表 2 相关参数 Tab. 2 Related parameters |
| 表 3 例子结果 Tab. 3 example results |
根据上面计算得出的策略,最小库存费用是4 110元。
2) 例2。
当节点1需求不确定时,5~10月需求概率分布如表 4所示。
| 表 4 需求概率分布 Tab. 4 Demand probability distribution |
经过计算,需求的平均值为120,方差为150,同时各个节点的提前期为1、3、5,且服务水平为98%。根据上文分析,应该确定出安全库存,98%的服务水平所对应的安全系数f=2.05,安全库存s=922.5, 则安全库存的费用为1 845元,此时最小费用为4 110+1 845=5 955元。
6 结语本文以供应链多级库存串行系统为研究对象,研究了考虑残次品、碳排放等影响的供应链库存持有成本、订购成本、运输成本和检查成本的构成函数,建立了供应链EOQ模型,为考虑残次品与碳排放的供应链多级库存控制提供依据。经过算例验证,结论有效,拓展了EOQ模型应用范围。未来研究方向:1)模型假设较理想,忽略检查时间,未考虑上游节点缺货、运输批次以及运输方式等问题;2)本文的碳排放仅在运输中考虑,未考虑在生产与库存持有中的碳排放;3)本文的研究对象是串行单链系统,现实应用需要将其扩展为网状供应链。
| [1] |
CLARK A J, SCARF H. Optimal policies for a multi-echelon inventory problem[J].
Management Science, 1960, 4(6): 475-490.
|
| [2] |
于莲, 范玉妹. 一类多级库存模型及其算法研究[J].
北京工商大学学报(自然科学版), 2007, 25(6): 79-81.
YU Lian, FAN Yumei. Study on model of multi-level inventory and its algorithm[J]. Journal of Beijing Technology and Business University(Natural Science Edition), 2007, 25(6): 79-81. |
| [3] |
段立江, 杜艳可, 阳平华. 供应链环境下的装备多级库存优化研究[J].
计算机工程与应用, 2009, 45(15): 206-208.
DUAN Lijiang, DU Yanke, YANG Pinghua. Optimization of equipment multi-echelon inventory in environment of SC[J]. Computer Engineer and Applications, 2009, 45(15): 206-208. DOI: 10.3778/j.issn.1002-8331.2009.15.060. |
| [4] |
曾艳. 需求确定的多级库存系统的库存策略[J].
集美大学学报(自然科学版), 2004, 9(1): 77-81.
ZENG Yan. Stationary politics in multi-echelon inventory systems with deterministic demand[J]. Journal of Jimei University (Natural Science), 2004, 9(1): 77-81. |
| [5] |
SALAMEH M K, JABER M Y. Economic production quantity model for items with imperfect quality[J].
International Journal Production Economics, 2000, 64(1): 59-64.
|
| [6] |
WAHAB M I M, MAMUN S M H, ONGKUNARUK P. EOQ models for a coordinated two-level international supply chain considering imperfect items and environmental impact[J].
International Journal Production Economics, 2011, 134(1): 151-158.
DOI: 10.1016/j.ijpe.2011.06.008. |
| [7] |
熊浩. 基于混合需求的供应链多级库存协同订货模型[J].
计算机应用, 2012, 32(9): 2631-2633.
XIONG Hao. Collaborative ordering models of multi-echelon inventory system based on hybrid demand[J]. Journal of computer applications, 2012, 32(9): 2631-2633. |
| [8] |
BLANCHINI F, MIANI S, RINALDI F. Guaranteed cost control for multi-inventory systems with uncertain demand[J].
Automatica, 2004, 40(2): 213-223.
DOI: 10.1016/j.automatica.2003.09.015. |
| [9] |
KIM G, WU K, HUANG E. Optimal inventory control in a multi-period newsvendor problem with non-stationary demand[J].
Advanced Engineering Informatics, 2014, 29(1): 139-145.
|
| [10] |
李兵, 付新玥, 刘金. 面向低碳的供应链节点最优库存控制策略[J].
统计与决策, 2012, 12(10): 44-46.
LI Bing, FU Xinyue, LIU Jin. Optimal inventory control strategy for low carbon supply chain nodes[J]. Statistics and Decisions, 2012, 12(10): 44-46. |
| [11] |
黄立. 碳约束下需求离散随机的库存控制问题研究[J].
物流科技, 2014, 10(25): 80-81, 85.
HUANG Li. Research on the problem of inventory control under discrete stochastic demand and carbon constraints[J]. Logistics Sci-Tech, 2014, 10(25): 80-81, 85. |
| [12] |
HAMMAMI R, NOUIRA I, FREIN Y. Carbon emissions in a multi-echelon production-inventory model with lead time constraints[J].
International Journal Production Economics, 2015, 164(1): 292-307.
|
| [13] |
屈晓龙, 李波. 碳限额与交易机制下零售商模糊库存模型优化求解[J].
北京理工大学学报(社会科学版), 2014, 16(6): 20-25, 33.
QU Xiaolong, LI Bo. Optimum solution of a fuzzy retailer's inventory model under the carbon "cap-and-trade"mechanism[J]. Journal of Beijing Institute of Technology(Social Sciences Edition), 2014, 16(6): 20-25, 33. |
| [14] |
蒋雨珊, 李波. 碳管制与交易政策下企业生产管理优化问题[J].
系统工程, 2014, 32(2): 150-153.
JIANG Yushan, LI Bo. Production management optimization problem under carbon cap and trade policy[J]. Systems Engineering, 2014, 32(2): 150-153. |
| [15] |
屈晓龙, 李波, 蒋雨珊. 模糊环境下含次品供应链成本与碳排放优化管理[J].
兰州大学学报(自然科学版), 2015, 51(2): 271-283.
QU Xiaolong, LI Bo, JIANG Yushan. Cost and carbon emission optimization management on a supply chain with defective items under fuzzy environment[J]. Journal of Lanzhou University(Natural Sciences), 2015, 51(2): 271-283. |
 2016, Vol. 19
2016, Vol. 19



