大规模复杂制造系统的性能分析一直是项非常困难的任务。以半导体封装测试系统为例,它相对于传统制造系统而言更为复杂:多资源搬运系统形成了复杂多环结构;生产流程繁复、具有可重入特性、生产过程中存在不确定性等等。这些复杂特性都加剧了这类系统性能分析的复杂度[1]。目前,这类以半导体封装测试系统为代表的复杂多环结构制造系统尚缺乏有效的性能分析方法[2]。
国内外关于制造系统性能分析的研究成果主要分为3大类,分别是精确解析方法、近似解析方法和仿真方法[3]。精确解析方法是对制造系统进行数学建模,并利用数学解析手段对模型进行求解,可以得到精确的系统性能结果。目前大部分精确解析方法都基于马尔科夫模型[4-6]。其缺点在于应用范围受限于简单的两设备制造系统[7]。近似解析方法则是以精确解析方法为基石,通过构建、求解近似解析方程分析系统性能[8]。该方法能够快速、近似地评估大规模制造系统的性能,但受限于精确解析方法的应用范围,现有的近似解析方法无法评估特性较为复杂的制造系统[9]。仿真方法可以为任意复杂程度的制造系统构建仿真模型并分析性能,但对系统使用者提出了很高的仿真建模能力要求,且仿真模型运行时间与系统复杂程度成正比,不适用于有大量案例需要分析的情况[10-11]。针对仿真方法的缺点,学者们提出了基于仿真的元模型(metamodel)方法[12]。元模型是仿真模型所体现的系统输入/输出关系的一种近似表达,使用最为广泛的元模型构建方法为人工神经网络(artificial neural network)模型[13-14]。从方法性能而言,元模型提供的是近似结果,其效率要高于仿真方法。但它的缺点在于:普适性差、准确性与效率不能兼顾[15]。
通过对国内外研究现状和发展动态进行综述分析后发现,将解析方法与元模型结合是解决复杂制造系统的有效途径。使用基于仿真的两设备制造系统元模型取代精确解析方法作为近似解析方法的基石可以解决精确解析方法无法分析复杂制造系统以及元模型方法普适性差的问题。在这个过程中,如何准确快速地构建两设备制造系统元模型是关键问题。为了解决这个关键问题,从两个方面开展了相关研究:一方面,选取在函数逼近方面表现优异的BP神经网络、RBF神经网络以及Chebyshev神经网络分别进行建模优化,通过比较分析确定最优配置神经网络模型,确保方法准确性;另一方面,开发数据驱动的仿真技术,通过仿真软件的VBA接口实现人工神经网络所需案例的自动获取,大幅提升方法效率。该研究方法的提出可以解决两设备制造系统的元模型构建问题,从而为半导体封装测试等复杂制造系统的性能分析方法提供有效支持。
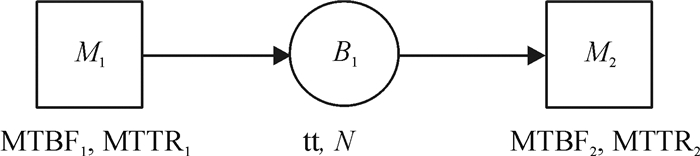
1 系统描述如图 1所示,本文所研究的系统由两台设备M1和M2组成,两台设备之间设一缓存B1。零件从系统外依次流经第1台设备和第2台设备后离开系统。两台设备的生产周期相同,设为1个单位时间。从设备M1搬运到设备M2的时间为tt,tt≤1。缓存B1的容量为N。
|
图 1 两设备系统 Fig. 1 Two-machine systems |
系统中的设备假设为不可靠,可能发生故障。考虑到现实制造系统中的实际情况,这里采用基于操作的故障机制,即设备只有在进行操作的过程中才有可能故障。设备的故障间隔时间和故障修复时间均设定为服从指数分布。对于设备Mi,平均故障间隔时间和平均故障修复时间分别为MTBFi和MTTRi。
当设备M1发生故障且与设备相邻的缓存位置没有零件时,设备M2处于饥饿停机状态,无法进行操作。当设备M2发生故障且缓存内零件数量达到缓存容量时,设备M1处于阻塞停机状态,无法进行操作。在该系统中,假设设备M1前有无数零件,永远不会处于饥饿停机状态,设备M2后有无限容量缓存,永远不会处于阻塞停机状态。
2 元模型分析元模型是仿真模型的进一步概括,它采用仿真模型的部分输入/输出结果(仿真案例)来构建输入/输出关系。因此,元模型提供的是近似的结果。本文要构建的元模型是一个多元输入/输出的模型(图 2),其本质是一个多元函数。一般而言,构建元模型方法有很多,包括田口模型、Kernel模型、一般线性模型、Kriging模型等等,但人工神经网络是其中应用最为广泛的元模型构建方法。尤其是在函数逼近方面,神经网络将前馈网络与函数逼近有机地结合起来,不仅提供了一个标准的逼近结构以及随着隐层个数改变而能达到任意精度的逼近工具,而且有标准的学习算法用以确定逼近函数的参数,同时处理的数据对象十分广泛:适用于大规模的、高度非线性的、不完备的数据处理[16]。因此,这里选取了3种典型的函数逼近神经网络模型:BP神经网络,RBF神经网络,Chebyshev神经网络来建立元模型。

|
图 2 元模型建模 Fig. 2 Metalmodeling |
BP神经网络的学习过程主要是正向和反向传播两个方面。这两个特点是模式前向传输和误差反向传输。函数逼近是它的最强大应用之一,即根据所训练的样本,对未知的函数类型进行逼近。
RBF神经网络具有的全局最优特性和最佳逼近性能,并且结构比较简单,训练速度较快,也是一种可以广泛运用于模式识别、函数逼近等领域的神经网络模型。RBF神经网络的核心是隐含层的设计,中心点和宽度的选取直接影响到神经网络的最终性能。
Chebyshev神经网络在使用时要注意将多输入-多输出系统分解成多输入-单输出系统。Chebyshev神经网络模型采用了较复杂的非线性激励函数,当用于逼近复杂非线性目标特性时,比BP神经网络的隐神经元个数少得多。相比于传统BP神经网络,Chebyshev神经网络只要调整隐层至输出层的权值,所以工作量减少了很多,加快了算法的收敛。
通过三者的比对优化可以选取获得最终的元模型。
3 数据驱动的仿真建模 3.1 两设备系统仿真建模人工神经网络所需的大量案例来自于仿真模型,因此本小节先根据系统描述来建立两设备系统的仿真模型。所采用的仿真软件为Arena。图 3展示了整个模型的运行机制。

|
图 3 Arena仿真模型流程图 Fig. 3 Flow chart of Arena simulation model |
在为系统构建仿真模型后,需要获取大量元模型构建所需的案例。案例获取包括系统配置、仿真模型运行、仿真结果记录等步骤。如手动执行这一过程将耗费大量的人力和时间,从而大大降低方法的效率和可行性。因此,本文基于VB软件设计开发了数据驱动的仿真平台,以实现案例获取的全自动化。
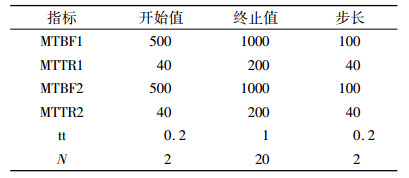
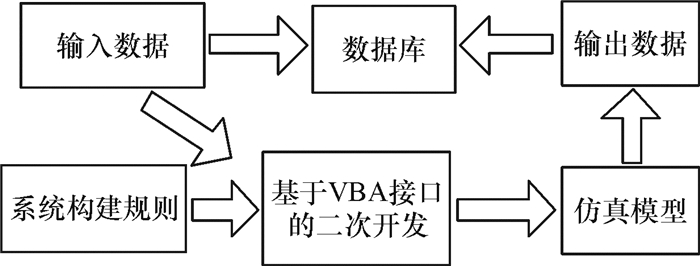
数据驱动仿真平台由输入数据、系统构建规则、基于VBA端口的二次开发、仿真模型、数据库、输出数据这六大模块构成(图 4)。其运行过程如下:根据元模型输入参数设计所要获取案例的输入数据,并将其储存至数据库;以系统构建规则为指导,对Arena软件进行基于VBA端口的二次开发,实现将每一案例的输入数据配置到预先构建的仿真模型中并运行仿真模型的功能;将每一案例对应的仿真模型运行结果,即输出数据,储存至数据库对应的位置,完成案例的获取工作。表 1给出了所有的输入数据。
|
图 4 数据驱动仿真平台框架结构图 Fig. 4 The structure diagram of data-driven simulation plantform |
| 表 1 输入指标 Tab. 1 Inputs index |
BP神经网络工具箱函数包括创建函数,传递函数,学习函数,训练函数,性能函数及现实函数。同样,根据不同的目的和学习要求,可以采用很多不同的BP算法。BP网络学习算法主要如下。
1) 最速下降BP算法(steepest descent backpropagation,SDBP);2)动量BP算法(momentum backpropagation,MPBP);3)学习速率可变的BP算法(variable learning rate backpropagation,VLBP);4)弹性算法(resilient back-PROPagation,RPROP);5)变梯度算法(conjugate gradient backpropagation,CGBP);6)拟牛顿算法(Quasi-Newton algorithms);7)LM(Levenberg-Marquardt)算法。
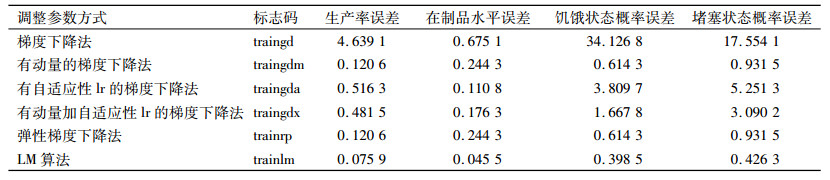
元模型构建需要兼顾收敛速度和精确性,因此对上述模型进行比较,选取最合适的算法。用之前得到的案例数据库进行函数逼近,使用Matlab编写程序并得出结果。神经元数量暂取50,从数据库中选取3 000样本案例进行分析,最后的误差分析见表 2。从表 2可以看出,在各种算法中,虽然LM算法用时最长,但其误差要远小于其他算法,可选定为BP神经网络的使用算法。
| 表 2 BP神经网络算法与仿真结果误差 Tab. 2 Error between BP neural network algorithm and simulation results |
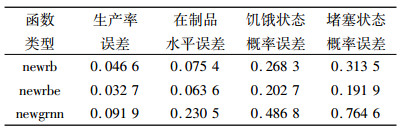
MATLAB神经网络工具箱提供了若干函数用于实现RBF神经网络,其中用于函数逼近的函数主要有newrb、newbe、newgrnn 3种。这里选择SPREAD为100对3种函数进行比较,结果见表 3。从表 3可以看出,3种函数中newrbe函数误差最小,可选定为RBF神经网络的算法。
| 表 3 RBF神经网络函数与仿真结果误差 Tab. 3 Error between RBF neural network algorithm and simulation results |
根据Chebyshev多项式定理,可以建立多输入Chebyshev神经网络。经过实验发现,由于输入的区间跨度很大,MTBF从500变化到700,而tt仅从0.2变化到1,一组输入的变化很大,所以权值变化很大,导致Chebyshev神经网络的精度不高。因此在这里不考虑基于正交基函数的神经网络模型。
5 元模型优化上节构建了BP神经网络元模型和RBF神经网络元模型,并确定了元模型的算法,本节将对以上2个元模型进行进一步的优化,主要分析BP神经网络的神经元数目和RBF神经网络的径向基函数密度对元模型精确性的影响。
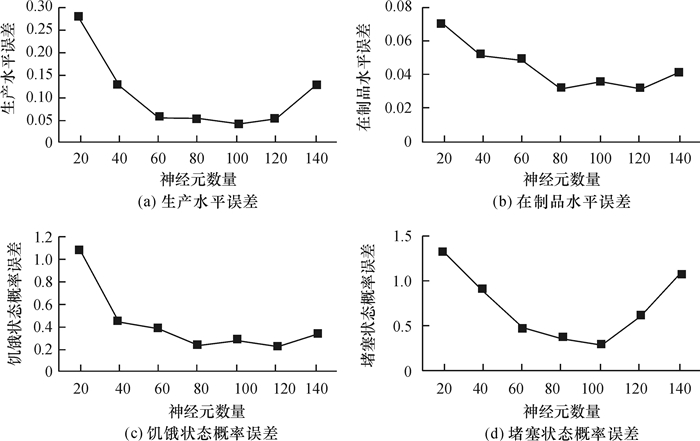
5.1 神经元数量对BP神经网络输出精度的影响在神经元的选取上,考虑到原始样本数量有45 000,如果每次都使用45 000个样本,会带来一个问题:神经元过多将造成系统内存不足。因此,本文选取3 000个样本来考量神经元对BP神经网络精度的影响。这里选择LM算法,神经元的数目分别为20,40,60,80,100,120,140,将元模型结果与仿真结果的误差对比,得到如图 5所示的4个结果对比图。
|
图 5 BP神经网络元模型与仿真模型输出结果误差图 Fig. 5 Error between BP neural network element model and simulation model |
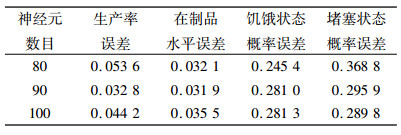
由图 5可知,当神经元数量在80~100附近时,模型精度最好。进一步设定神经元数量为90进行比较,发现当神经元数量为90时,误差最小(参见表 4)。因此在本案例里神经元数量取90。
| 表 4 BP神经网络元模型输出误差与神经元数目关系表 Tab. 4 Relationship between output error of BP neural network model and neuron number |
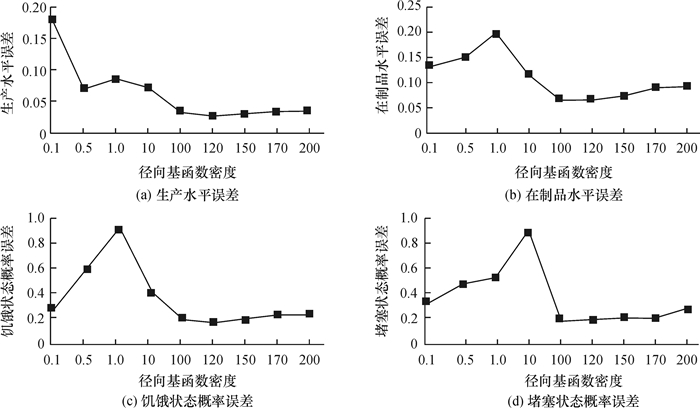
径向基函数因为其自身特性,收敛较快。为了将其与BP神经网络作比对,同样选取3 000个样本进行测试。径向基函数有两个参数, 径向基函数密度(spread),即扩展速度,和最大神经元数目需要确定。在径向基函数中,网络会从0个神经元开始训练,通过检查输出误差使网络自动增加神经元。每次循环使用,重复过程直到误差达到要求。考虑到RBF网络这种结构自适应确定的特点,本文只控制最大神经元数目,仅就径向基函数密度进行敏感性分析。这里径向基函数密度取0.1,0.5,1,10,100,120,150,170,200,同时选择newrbe函数。将RBF神经网络模型结果与仿真结果进行误差对比,得到如图 6所示的4个结果对比图。
|
图 6 RBF神经网络元模型与仿真模型输出结果误差图 Fig. 6 Error between RBF neural network element model and simulation model |
由图 6可以看出,在径向基函数密度为100~150时,误差最小。经过进一步细化区间,得到表 5。
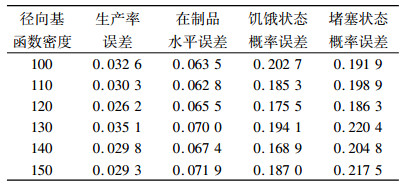
| 表 5 RBF神经网络元模型输出误差与径向基函数密度关系表 Tab. 5 Relationship between output error of RBF neural network model and SRREAD |
由表 5可得,当径向基函数密度在120时,误差值最小,因此本案例中SPREAD取120。
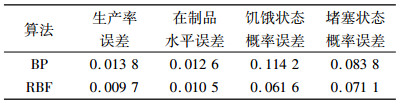
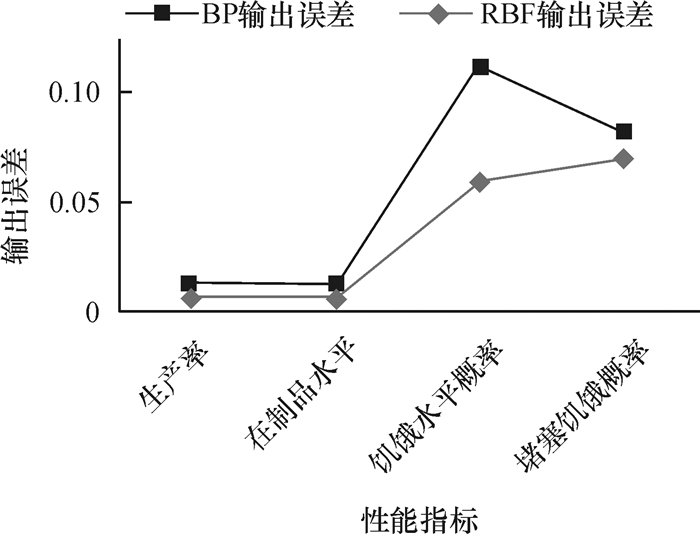
5.3 数据分析根据上文的优化分析,最终BP神经网络选择神经元个数为90,RBF神经网络径向基函数密度取120。为进一步比对分析这2个模型,本节在数据库的中随机选取145个输入,将两个模型的输出与仿真结果进行比较,最终得到如表 6所示的误差分析,并绘制成图 7以便更直观地观测结果。
|
图 7 BP神经网络与RBF神经网络结果误差对比图 Fig. 7 Comparison of error between BP neural network and RBF neural network |
| 表 6 BP神经网络与RBF神经网络结果误差对比表 Tab. 6 Comparison of error between BP neural network and RBF neural network |
由图 7可知RBF网络的各项性能都高于BP神经网络,对制造系统的性能分析精确度更高。通常来说,BP神将网络用于函数逼近时权值采用的负梯度下降法有一定的局限性。而RBF神经网络在逼近能力、学习速度上都占优势,且先前研究表明RBF神经网络可以以任意精度逼近任意连续函数,并能克服局部最小值问题。在本例中,由于输入输出之间的关系并不是连续函数,因此需要进一步比较两种神经网络的优劣。通过以上案例分析证明,在本例中,RBF神经网络表现要优于BP神经网络。
6 结论对半导体封装测试系统的性能分析,两设备系统元模型是基础环节。基于数据驱动仿真技术的元模型研究构建了考虑缓存输送时间的两设备系统元模型,并比较了3种神经网络模型对两设备系统的函数逼近能力。研究结果表明:RBF神经网络的函数逼近效果最好,其构建的元模型精度最高。下一步的工作是在该元模型基础上通过近似解析方法提出面向大规模半导体封装测试系统的性能分析方法,从而实现近似解析方法与仿真方法的有效结合,为大规模复杂制造系统的性能分析研究提供了一条新的研究思路。本文的工作不仅具有学术意义,还可以应用于封装测试系统的设计、优化,具有很高的实践价值。
| [1] |
李娜. 具有多环特性的半导体封装测试系统性能分析[D]. 北京: 清华大学, 2008.
LI N. Performance analysis of multi-loop closed semiconductor manufacturing [D]. Beijing: Tsinghua University, 2008. |
| [2] |
LI N, JIANG Z, LIU G, et al. Analysis of quality-caused re-entrance electrical test system in semiconductor manufacturing by Markov method[J].
International Journal of Production Research, 2011, 50(12): 3486-3497.
|
| [3] |
DALLERY Y, GERSHWIN S B. Manufacturing flow line systems: a review of models and analytical results[J].
Queueing Systems, 1992, 12(1): 3-94.
|
| [4] |
LIU J, YANG S, WU A, et al. Multi-state throughput analysis of a two-stage manufacturing system with parallel unreliable machines and a finite buffer. European Journal of Operational Research. 2012, 219(2): 296-304.
|
| [5] |
GEBENNINI E, GERSHWIN SB. Modeling waste production into two-machine-one-buffer transfer lines. IIE Transactions. 2013, 45(6): 591-604.
|
| [6] |
XIA B, CHEN J, ZHANG Z. An exact method for the analysis of a two-machine manufacturing system with a finite buffer subject to time-dependent failure[J].
Mathematical Problems in Engineering, 2015(4): 1-11.
|
| [7] |
LI J, BLUMENFELD D E, HUANG N, et al. Throughput analysis of production systems: recent advances and future topics[J].
International Journal of Production Research, 2009, 47(14): 3823-3851.
DOI: 10.1080/00207540701829752. |
| [8] |
GERSHWIN S B. An efficient decomposition method for the approximate evaluation of tandem queues with finite storage space and blocking[J].
Operations Research, 1987, 35(2): 291-305.
DOI: 10.1287/opre.35.2.291. |
| [9] |
PAPADOPOULOS H T, HEAVEY C. Queueing theory in manufacturing systems analysis and design: a classification of models for production and transfer lines[J].
European Journal of Operational Research, 1996, 92(1): 1-27.
DOI: 10.1016/0377-2217(95)00378-9. |
| [10] |
齐继阳, 竺长安. 基于DELMIA_QUEST制造系统仿真模型的研究[J].
机械设计与制造, 2010(4): 113-115.
QI J Y, ZHU C A. Research on simulation model of the manufacturing system based on DELMIA_QUEST[J]. Machinery design and Manufacture, 2010(4): 113-115. |
| [11] |
张志清, 凡艳, 程庆章. 医药物流中心人工拣选作业流程优化及仿真[J].
工业工程, 2015, 18(6): 26-31.
ZHANG Z Q, FAN Y, CHENG Q Z. Optimization of manual picking at medicine logistics center[J]. Industrial Engineering Journal, 2015, 18(6): 26-31. |
| [12] |
KLEIJNEN J P C. Krigingmeta modeling in simulation: a review[J].
European Journal of Operational Research, 2009, 192(3): 707-716.
DOI: 10.1016/j.ejor.2007.10.013. |
| [13] |
夏蓓鑫. 基于广义指数分布的制造系统性能解析评估方法研究[D]. 上海: 上海交通大学, 2013.
XIA B X. Study on analytical methods for performance evaluation of manufacturing systems based on generalized exponential distribution [D]. Shanghai: Shanghai Jiao Tong University, 2013. |
| [14] |
PALIWAL M, KUMAR U A. Neural networks and statistical techniques: A review of applications. Expert Systems with Applications. 2009, 36 (1): 2-17.
|
| [15] |
KHOSRAVI A, NAHAVANDI S, CREIGHTON D. A prediction interval-based approach to determine optimal structures of neural network meta models[J].
Expert Systems with Applications, 2010, 37(3): 2377-2387.
DOI: 10.1016/j.eswa.2009.07.059. |
| [16] |
董瑞. 基于神经网络的函数逼近方法研究[D]. 吉林: 东北师范大学, 2011.
DONG R. Study on the function approximation based on neural network [D]. Jilin: Northeast Normal University, 2011. |
 2016, Vol. 19
2016, Vol. 19