近年来,突发性自然灾害和人为事故所造成的危害程度正在不断增加,提高突发事件下的应急管理能力逐渐成为了管理学界的研究重点和热点。在突发事件处置工作中,不可避免地要处理大量应急或救援物资,因而应急物流管理成为应急突发事件管理中的核心问题之一。而应急设施选址问题又有着独特的地位,是应急物资管理的基础和出发点,是不可或缺的重要组成部分。本文主要针对应急物资集散中心的选址开展研究。
1 文献综述 1.1 应急设施选址问题国内外学者针对应急设施选址问题一直在进行不懈的研究。与普通选址问题类似,应急设施选址问题的模型主要有3种:覆盖(covering)模型、p-中值(p-median)模型、p-中心(p-center)模型[1, 3-4]。这3类模型的主要区别在于优化目标不同,覆盖模型的目标是以最少的设施覆盖所有需求点或者是寻求覆盖最大比例的需求点;p-中值模型以优化需求点和设施之间的总距离(成本)为目标;p-中心问题则体现了公平性的思想,以优化需求点和设施之间最大距离为目标。不同的目标使这3类模型可适用于不同类型的突发事件,Jia等[4]将3种模型分别用于应对脏弹、炭疽热、天花病毒3种恐怖袭击的救灾物资储备设施选址。Guan等[5]将轴-辐式网络模型与覆盖模型相结合用于应急设施选址,应用网络中的枢纽应对突发事件。王成等[6]提出一种基于覆盖率的递归k-means选址方法,可以自动计算出某区域所需要的应急设施数量和位置。樊博[7]应用空间聚类技术研究了应急服务机构的选址问题,通过采用聚类分析的数据模型,在改进既有空间聚类算法的基础上,提出以k-means聚类算法缩减解空间的搜索范围、以模拟退火算法为寻优搜索策略,并基于GIS系统提出一种空间聚类算法,以实现应急救援设施的选址。Zhang等[8]针对应急物流系统提出了一个基于节点加权的瓶颈斯坦纳树多目标选址优化模型,并利用细胞随机扩散搜索方法来对此选址优化模型进行求解。黄向荣等[9]则考虑到大型突发事件的突发性、不确定性以及食品在运输和存储过程中易腐受损等特点,建立了一个针对食品物流应急配送中心选址的评价指标体系,并在此基础上建立了一个基于蚁群算法和径向基神经网络相结合的选址模型。Gang等[10]在双层选址模型中应用机会约束来表示环境的不确定性,并引入满意度的指标保证上层政府和下层所有需求点的公平性。
1.2 鲁棒选址问题针对自然灾害的应急物流系统建模中,一个不可回避的因素是设施损毁问题。Drezner[11]首先提出了考虑设施可靠性的选址问题,在应急管理中具有很强的实际意义。朱建明[12]在设施损毁情景的基础上提出了一种应急设施选址的多目标决策方法,用覆盖为目标反映救援时效性,最大救援半径反映均衡性,设施损毁情境下额外增加的救援变更时间反映鲁棒性。在突发事件中,鲁棒优化(robust optimization)方法注重在有限的信息下,使不确定情景中最坏情况下的目标最优,这能够保证在应急救援中的决策在任何条件下不会得到太差的结果。随着事件发展,不确定性的降低,利用鲁棒优化可引入新信息实现后续策略调整,得到更好的结果[2]。葛春景等[13]在集覆盖轴-辐网络模型的基础上,提出了应急服务设施轴-辐网络布局的双重鲁棒优化模型,用鲁棒偏差系数控制鲁棒解与预设情境下最优解之间的最大出行时间的偏差以及目标函数值的偏差。张玲等[14]提出了一个基于不确定需求的二阶段应急资源配置模型,并应用可调整鲁棒优化方法进行求解。张玲等[15]提出了基于情景的最小最大后悔值准则的应急设施选址-调度鲁棒优化模型,并利用情景松弛的迭代算法进行求解。冯春等[16]在需求不确定的情景下,提出了一个有最大运输距离限制的应急物资储备库选址问题鲁棒优化模型。Lu[17]提出了一个鲁棒p-center选址模型,用区间数来表示物流成本和需求的不确定性集合,以最差情况下最大需求加权距离和最优最大需求加权距离的偏差为优化目标,提出了一个能在该模型下识别最差情景的定理,并根据该定理使用遗传算法和模拟退火算法对模型进行求解。Zeng等[18-19]基于经典的鲁棒优化模型提出一个两阶段鲁棒p-median选址混合整数规划模型,在考虑设施可靠性条件下,以最差情境下的性能最优为目标,在第1阶段得到具有鲁棒性的选址方案,同时隐含了第2阶段情景发生时的调整决策,并设计一种精确算法来求解这一问题。
由于突发事件往往前兆不充分,具有明显的复杂性特征,尤其是信息具有高度不确定性,且随着时间的推进呈动态变化规律,因此决策活动也是一个递进和序贯的过程。突发事件发生时,预先安排好的方案可能无法顺利实施,有效的解决手段是寻找一个高鲁棒性的预规划,并在实际运作过程中针对发生的变化和新信息对初始规划进行修正。在前述研究的基础上,本文考虑需求和成本变动、设施损毁的不确定性,提出了一种应急设施选址问题两阶段鲁棒优化模型,第1阶段为鲁棒性的“预选址”,模型在传统的p-center选址模型基础之上,又同时考虑了选址策略在灾后、新设施建立前后的性能需求;第2阶段为基于反应式修复和调整策略的新建设施“重选址”,以综合成本最小为目标。与文献[18]中的p-median鲁棒选址模型相比,本文采用的p-center选址模型更能体现公平性,更符合应急突发事件的特征;在“预选址”模型中不仅考虑新建设施,同时考虑了灾后反应的需求;本文的第2阶段“重选址”模型是在“预选址”策略的基础之上,针对新信息做出重建设施的决策。最后通过算例分析,表明了本文模型得到的鲁棒性选址策略的可行性;并通过与传统p-center模型的对比,体现了本文模型所得策略的优越性与合理性。
2 应急设施选址问题两阶段鲁棒优化模型p-center模型能够体现对于每个需求点公平性。本文基于这一出发点,在传统p-center模型基础上考虑预选址与重选址2个阶段,预选址决策同时考虑灾前规划、灾后反应、设施重建3个时段的最大需求加权成本,得到具有鲁棒性的预规划;重选址在预选址和实际灾情的基础之上,以最小的综合成本进行新建设施及设施分配的重新规划,在最小综合成本中,考虑了由于物资重新分配所产生的调整成本和计划变更所带来的不便,因此目标函数同时包括了性能指标和鲁棒性指标。
2.1 问题描述突发事件发生前,决策者无法获得准确的信息,只能根据可能发生的情景、需求和成本的估计值来进行预选址规划;突发事件发生后,新的需求和成本信息随之出现,此时部分应急设施点被破坏,而未被破坏的设施可满足部分需求;最后,决策者根据新信息选择未被破坏的地点新建设施,并满足剩余需求。
针对以上问题,假定平面上存在2个集合,分别是需求点集合和可选设施点集合。在不考虑设施容量的前提下,已知:所有需求点在灾难发生时的预期需求;任意两点间在正常情况下的运输成本;灾难发生时,设施点破坏情况的情景集合(假设每个情境下都有若干个可选设施点受灾使得位于这些点的设施被破坏,并且设施不能在原地重建);每个情景发生时,任意两点间的运输成本;每个情景发生时,重建设施前的预期需求和重建设施后的预期剩余需求;设施数量上限为p。
定义参数及决策变量如下。
1) 参数。
I为需求点集合;
J为可选设施点集合;
K为情景集合;
k={kj|j∈J}∈K为情景;若设施点j损毁,则kj=1,否则kj=0。
cij为i, j两点间正常情况下的单位运输成本;
di为i点的需求;
p为设施数量上限;
cij(k)为情景k发生时,i, j两点间单位运输成本;
di(k)为情景k发生时,重建设施前,i点的需求;
di'(k)为情景k发生时,重建设施后,i点的剩余需求;
B为新建设施的成本;
Lmax为每个需求点的运输成本最高预算;
α1, α2, α3, γ为权重。
2) 决策变量。
yj:当点j被选择修建设施时为1, 否则为0;
xij:需求点i被分配至设施j时为1, 否则为0;
wij:新建设施前,需求点i的需求由设施j满足时为1, 否则为0;
uj:在点j为新建设施时为1, 否则为0;
vij:新建设施后,需求点i被分配至设施j时为1, 否则为0。
2.2 鲁棒p-center预选址模型
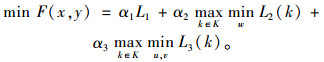
|
(1) |
subject to
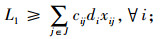
|
(2) |
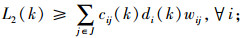
|
(3) |
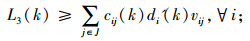
|
(4) |
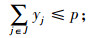
|
(5) |
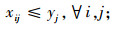
|
(6) |
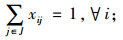
|
(7) |
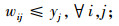
|
(8) |
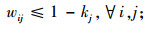
|
(9) |
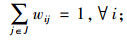
|
(10) |
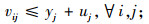
|
(11) |
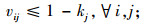
|
(12) |
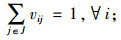
|
(13) |
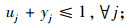
|
(14) |
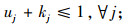
|
(15) |
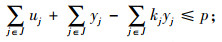
|
(16) |
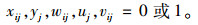
|
(17) |
式(1)为目标函数,由3个部分组成,L1为灾前需求点与设施之间的最大运输成本,L2为灾后情境k下设施重建前,需求点与设施之间的最大运输成本,L3为灾后情境k下设施重建后,需求点与设施之间的最大运输成本;式(5)限制设施数量不超过p个;式(6)表示修建设施的节点才能服务于需求点;式(7)表示每个需求点由一个设施服务,同式(10)和(13);式(8)和(9)表示仅当j点有设施、且该设施未被破坏时,才能在灾后设施重建前服务于需求点;式(11)和(12)含义类似,只有在灾前或灾后修建设施的设施点才能服务于需求点;式(14)和(15)表示只有未修建设施且未被破坏的设施点才能新建设施;式(16)为灾后设施数量限制。
2.3 重选址模型
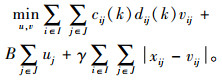
|
(18) |
subject to
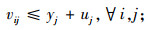
|
(19) |
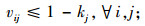
|
(20) |
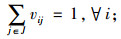
|
(21) |
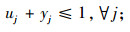
|
(22) |
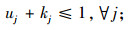
|
(23) |
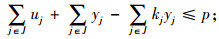
|
(24) |
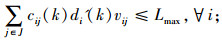
|
(25) |
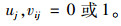
|
(26) |
在第2阶段的重选址模型中,式(18)由3个部分的成本组成:总运输成本、新建设施的成本和需求点重分配产生的调整成本。约束中式(19)~(24)与第一阶段模型中式(11)~(16)的意义相同,式(25)为每个需求点设置了运输成本最高预算,保证一定的公平性。
3 算例分析在100×100的平面上,随机生成10个需求点、6个设施候选点及其相应的初始需求。假设存在3个不同情景(随机生成设施损坏情况,每个情景下损坏的设施数量不超过2个),且在第2阶段随机选择实际发生的情景。其它参数设置如下。取p=3;α1=0.3, α2=0.2, α3=1,B=2 000,γ=1 000,Lmax=15 000。本文使用CPLEX软件对2个阶段的模型进行求解。
为便于求解,将模型目标转化为式(27)所示的等价形式。
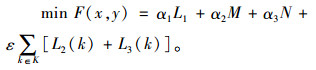
|
(27) |
其中,ε为一个充分小的常数,可保证式(1)与式(27)同时达到最小;M、N分别为设施重建前后最坏情景下的运输成本,也即满足
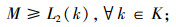
|
(28) |

|
(29) |
为分析和评估本文模型的有效性,分别采用了本模型和传统p-center模型对随机生成的算例进行了计算。一组典型数据的计算结果如图 1与表 1所示,分别显示了灾前规划、灾后应急响应(设施新建前)、以及设施新建后的选址与设施分配策略及相应的成本,其中图 1(a)部分表示本文模型结果,图 1(b)部分表示传统p-center模型结果。图中还表示出了“预选址—重选址”二阶段鲁棒优化模型的运作流程。图 1(a)-1与图 1(b)-1中表示第1阶段的“预选址”规划;图 1(a)与图 1(b)-2表示灾难实际发生后剩余设施对需求点的最佳服务情况;图 1(a)-3与图 1(b-3)表示第2阶段的重新选址和分配规划。表 1中的计算结果包括灾前规划、灾后反应和设施重建3个时段需求点与设施之间的最大运输成本,以及重选址阶段的综合成本、总运输成本、设施建设成本、需求分配调整成本。其中,灾前规划的最大运输成本即为前文模型中的L1。

|
图 1 鲁棒p-center模型与传统p-center模型的对比 Fig. 1 Comparing of robust p-center model and traditional p-center model |
| 表 1 鲁棒p-center模型与传统p-center模型的对比1) Tab. 1 Comparing of robust p-center model and traditional p-center model |
在灾前规划阶段,2个模型得到了不同的选址方案,可以看出p-center模型给出的选址方案中3个设施的分布较为分散,但最大运输成本较小;灾难发生后,2种方案均只有一个设施幸存,此时由于传统p-center模型的方案中剩余设施的位置较为偏远,造成最大运输成本较高,所以本文模型方案中剩余设施具有更好的反应能力;在设施重建阶段,2种方案均只新建了一个设施,但由于预规划的需求分配不同以及调整成本的限制,2种方案产生了不同的运输成本和需求分配调整成本。
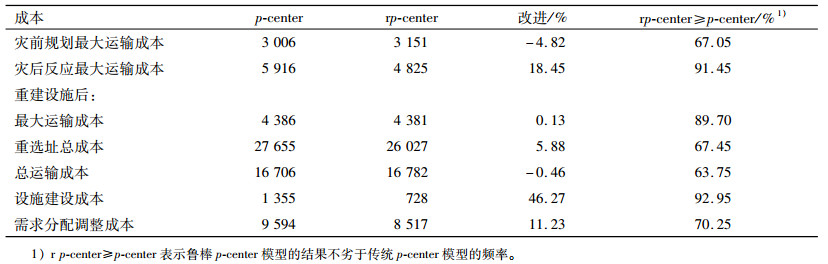
随机产生2 000组数据并计算得出表 2。可以看出,本文的模型在大部分情况中优于传统p-center模型,在灾前规划阶段损失很少性能的前提下,能够显著的降低灾难发生后的最大运输成本,并减少综合成本,特别是设施建设成本和需求分配调整成本。
| 表 2 鲁棒p-center模型与传统p-center模型计算结果对比 Tab. 2 Computational results of robust p-center model and traditional p-center model |
传统的物流设施选址通常是固定位置的,而突发事件发生时,应急物流设施的设置往往具有临时性和动态性,可能会随着事件发展需要和新信息的获取而有所调整。本文基于p-center选址模型,提出了一个应急设施选址问题两阶段鲁棒优化模型,在需求和成本变动、设施损毁存在不确定因素的情况下,首先进行鲁棒性的“预选址”,并在灾难发生后进行反应式的“重选址”。算例分析说明了与传统p-center选址模型相比,两阶段鲁棒优化模型解决应急设施选址问题的有效性。
在实际的应急管理中,可能会遇到更加复杂的问题,所以将本文的模型应用于实际案例的研究将能够进一步对模型进行验证;解决大规模的鲁棒优化选址问题时,精确算法将不再适用,需要针对问题特点开发启发式算法来获得更好的性能;在未来的研究中,可以考虑将应急管理的其它环节与选址问题相结合的集成鲁棒优化,进一步提高应急救援的效率。
| [1] |
DREZNER E. Facility location: a survey of applications and methods[M]. New York: Springer, 1995:9-260.
|
| [2] |
BEN-TAL A, EL GHAOUI L, NEMIROVSKI A. Robust optimization[M]. Princeton: Princeton Univ Press, 2009.1-145.
|
| [3] |
陈志宗, 尤建新. 重大突发事件应急救援设施选址的多目标决策模型[J].
管理科学, 2006, 19(4): 10-14.
CHEN Zhizong, YOU Jianxin. A multi-objective decision model of emergency rescue facility location for large-scale emergency incidents[J]. Management Sciences in China, 2006, 19(4): 10-14. |
| [4] |
JIA H, ORDÓÑEZ F, DESSOUKY M. A modeling framework for facility location of medical services for large-scale emergencies[J].
IIE Transactions, 2007, 39(1): 41-55.
DOI: 10.1080/07408170500539113. |
| [5] |
GUAN X, GE C, WANG X, et al. Models and algorithms for hub and spoke locations for emergency service facilities in eesponse to serious emergency incidents[J].
Human and Ecological Risk Assessment: An International Journal, 2013, 19(2): 553-565.
DOI: 10.1080/10807039.2012.746144. |
| [6] |
王成, 关蓉, 王惠文. 基于覆盖率的递归k-均值方法及其在应急系统选址布局中的应用[J].
数学实践与认识, 2016, 46(3): 69-76.
WANG Cheng, GUAN Rong, WANG Huiwen. Coverage-rate-based recursive k-means clustering method: an application of location problem in emergency system[J]. Mathematics in Practice and Theory, 2016, 46(3): 69-76. |
| [7] |
樊博. 基于空间聚类挖掘的城市应急救援机构选址研究[J].
管理科学学报, 2008, 11(3): 16-28.
FAN Bo. Spatial clustering mining method for site selection problem of emergency response center[J]. Journal of Management Sciences in China, 2008, 11(3): 16-28. |
| [8] |
ZHANG J, DONG M, FRANK C F. A bottleneck Steiner tree based multi-objective location model and intelligent optimization of emergency logistics systems[J].
Robotics and Computer-Integrated Manufacturing, 2013, 29(3): 48-55.
DOI: 10.1016/j.rcim.2012.04.012. |
| [9] |
黄向荣, 谢如鹤. 基于蚁群算法与RBF神经网络模型的突发应急配送决策[J].
统计与决策, 2009(15): 56-58.
HUANG Xiangrong, XIE Ruhe. The emergency distribution decision-making based on ant colony algorithm and RBF neutral network model[J]. Statistics and Decision, 2009(15): 56-58. |
| [10] |
GANG J, TU Y, LEV B, et al. A multi-objective bi-level location planning problem for stone industrial parks[J].
Computers & Operations Research, 2015, 56: 8-21.
|
| [11] |
DREZNER Z. Heuristic solution methods for two location problems with unreliable facilities[J].
Journal of the Operational Research Society, 1987, 38(6): 509-514.
DOI: 10.1057/jors.1987.88. |
| [12] |
朱建明. 损毁情景下应急设施选址的多目标决策方法[J].
系统工程理论与实践, 2015, 35(3): 721-727.
ZHU Jianming. Methods of multi-objective decision-making for emergency facility location problem under failure scenario[J]. System Engineering-Theory & Practice, 2015, 35(3): 721-727. |
| [13] |
葛春景, 王霞, 关贤军. 应急服务设施轴辐网络布局的λ-鲁棒优化[J].
工业工程与管理, 2010, 15(6): 45-57.
GE Chunjing, WANG Xia, GUAN Xianjun. λ-Robust optimization of emergency service facilities hub-and-spoke network response for large-scale emergency[J]. Industrial Engineering and Management, 2010, 15(6): 45-57. |
| [14] |
张玲, 王晶, 黄钧. 不确定需求下应急资源配置的鲁棒优化方法[J].
系统科学与数学, 2010, 30(10): 1283-1292.
ZHANG Ling, WANG Jing, HUANG Jun. Robust optimal resource allocation model for uncertain demands[J]. Journal of System Science and Mathematical Science, 2010, 30(10): 1283-1292. |
| [15] |
张玲, 陈涛, 黄钧. 基于最小最大后悔值的应急救灾网络构建鲁棒优化模型与算法[J].
中国管理科学, 2014, 22(7): 131-139.
ZHANG Ling, CHEN Tao, HUANG Jun. Emergency network model and algorithm based on min-max regret robust optimization[J]. Chinese Journal of Management Science, 2014, 22(7): 131-139. |
| [16] |
冯春, 于彧洋. 不确定情景下应急物资储备库选址问题研究[J].
工业工程, 2014, 17(2): 7-11.
FENG Chun, YU Yuyang. Research on emergency supply stockpile location under uncertainty scenarios[J]. Industrial Engineering Journal, 2014, 17(2): 7-11. |
| [17] |
LU C C. Robust weighted vertex p-center model considering uncertain data: An application to emergency management[J].
European Journal of Operational Research, 2013, 230(1): 113-121.
DOI: 10.1016/j.ejor.2013.03.028. |
| [18] |
AN Y, ZENG B, ZHANG Y, et al. Reliable p-median facility location problem: two-stage robust models and algorithms[J].
Transportation Research Part B: Methodological, 2014, 64: 54-72.
DOI: 10.1016/j.trb.2014.02.005. |
| [19] |
ZENG B, ZHAO L. Solving two-stage robust optimization problems using a column-and-constraint generation method[J].
Operations Research Letters, 2013, 41(5): 457-461.
DOI: 10.1016/j.orl.2013.05.003. |
 2016, Vol. 19
2016, Vol. 19