学习效应是生产过程由于人的经验积累,生产率提高与成本随产量增加而递减的过程,并且这种递减呈现出规律性。学习效应不仅在生产过程中存在,而且在质检过程中也存在。产出率具有学习效应,则生产单位产品的成本越来越低;质检过程具有学习效应,则质检成本越来越低。学习效应对最优生产策略有着重要的影响,因而探讨生产过程与质检过程具有学习效应的经济生产批量模型具有重要的现实意义。
Wright[1]在1936年提出了学习曲线理论,之后诸多学者对学习曲线进行广泛的拓展与应用。Salameh等[2]在假设需求为常数的条件下,将学习效应引入到EPQ模型中,但没有考虑缺陷品对最优生产策略的影响。Chen等[3]采用平均生产率的方法建立了允许缺货的产出率具有学习效应的EPQ模型。Mahata[4]在文献[3]的基础上,采用平均产出率的方法,建立了产出率具有学习效应和缺陷品数量具有模糊数属性的EPQ模型。Teng等[5]分析了产出率具有学习效应对EPQ模型中的最优信用支付期及最优生产批量的影响。Khan等[6]建立了质检过程具有学习效应的EOQ模型。Balkhi[7]采用Wright学习曲线形式,探讨了生产率具有学习效应及时变需求与缺货部分延期供给的易逝产品的EPQ模型。Kumar等[8]在模糊随机环境下,探讨了生产率具有学习效应的缺陷品可以返工处理的的EOQ模型。Dar-El等[9]认为虽然Wright学习曲线整合了学习过程中的认知因素和技能因素,但是Wright学习曲线模型没有区分认知和技能学习,Dar-El等提出了双重学习曲线模型。Jaber等[10]通过对初始生产时间的划分,改进了Dar-El等人的模型,并运用到了经典的EPQ模型中。Jaber等[11]在假设学习效应存在投资成本的情形下,建立了生产率具有学习效应的制造与再制造混合生产批量模型。
由于生产过程中的设备老化、工人技术水平的参差不齐和其他不确定性因素,生产中的缺陷品广泛存在,缺陷品的存在使得最优生产策略发生改变。关于缺陷品的EPQ模型,Salameh等[12]建立了具有缺陷品的EPQ模型,并与经典的EPQ/EOQ模型进行了对比。Jaber等[13]建立了质量改善具有学习效应的EPQ模型,由于质量改善学习效应的存在,产品的缺陷率越来越低。Wahab等[14]考虑合格品与缺陷品不同单位存储成本对文献[12]与[13]进行了拓展。Mukhopadhyay等[15]在存在排污成本前提下,扩展了缺陷品可以返工处理的EPQ模型。国内学者柏庆国等[16]针对非变质产品的生产存贮问题和易变质产品的存贮问题,考虑订购过程具有学习效应,分别建立了混合整数约束优化模型以及无约束优化模型。徐健腾等[17]不仅考虑生产过程中具有学习效应,而且考虑零售商分销过程中具有学习效应,得出了系统的最优策略。于秀丽等[18]考虑员工学习效应,分析了生产进度受员工技能差异和变化的影响。鲜见学者研究考虑质检过程中的学习效应。
本文与现有文献的不同在于,本文在经济生产批量模型中同时考虑产出和质检具有学习效应。以往对经典EPQ进行拓展时,忽略了原材料的存储成本,本文在建模过程中考虑原材料的成本,并且由于产出学习效应的存在,原材料呈现加速消耗趋势。由于生产过程的不完备,在生产过程中存在缺陷品,本文在建模过程中考虑缺陷品的存在。本文的研究扩展了经典经济生产批量模型,为生产管理者提供了决策依据。
1 模型描述、假设与变量说明制造商的产成品由3类原料按1:1:1的比例加工而成。制造商对生产完的产成品进行质量检验。质检过程滞后于生产过程,且质检速率小于产出率。制造商在生产与质检过程中存在学习效应,生产和质检单位产品的时间越来越短。由于生产过程的不完备,在生产过程中存在缺陷品。产出率学习效应的存在使得原材料的消耗呈现加速消耗趋势。
本文模型的建立基于如下假设。
1) 生产过程中产出率存在学习效应,学习系数为常数δ。质检过程中存在学习效应,学习系数为ε。
2) 制造商边生产边销售产品,面临的需求为D。
3) 由于生产过程的不完备,在生产过程中存在缺陷品,缺陷率为γ。制造商在对所有产品质检完成后,将缺陷品集中处理掉。
4) 生产库存模型运行在无限计划期内。
5) 在初始质检过程中,缺陷品均可检出,不考虑质检过程中存在的质检错误。
本文模型中用到的参数和变量定义如下。
K为生产第1个产品的时间(d);
χ为质检第1件产品所需要的时间(d);
A为生产准备费用(元/周期);
L为单位时间的劳动费用(元/d);
Cm为单位产成品的原料采购成本(元);
Ch0为单位时间单位产成品的存储费(元/d);
Ch1、Ch2、Ch3分别为原料1、原料2、原料3的单位时间单位存储成本(元/d);
Cs为单位产品的质检费用(元/单位);
t*为最优时间(d);
Tpi为第i个周期制造商的生产时间(d);
Tsi为第i个周期制造商的质检时间(d);
Ti为第i个周期的时间长度(d);
Xi为第i个周期的生产数量;
I(t)为t时刻的库存水平;
Ip(t)为在[0, tpi]时间段内产成品库存水平;
Id1(t)为在[tpi, tsi]时间段内的产成品库存水平;
Id2(t)为在tsi, T时间段内的产成品库存水平。
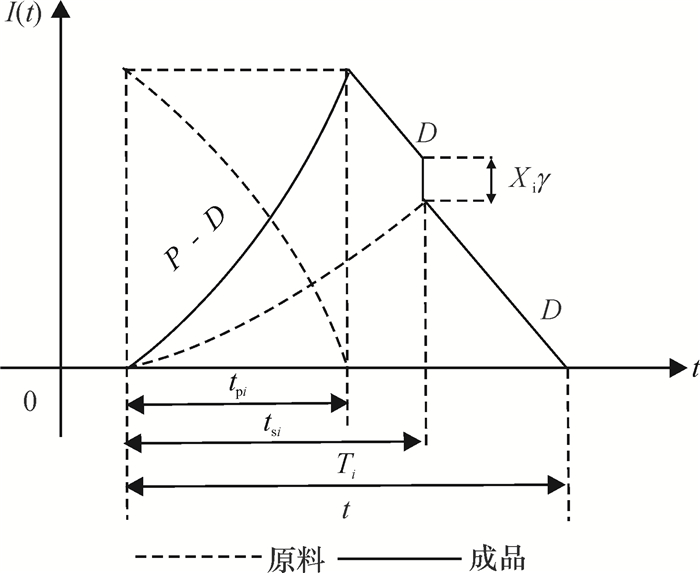
2 学习效应下的生产库存模型 2.1 生产库存成本模型图 1反映了原料与成品库存水平随时间变化情况。根据Wright学习曲线理论,生产第X件产品的工时为tX=KX-δ。生产一批X件产品的生产总工时为
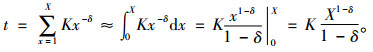
|
(1) |
|
图 1 原料与成品库存水平随时间变化趋势图 Fig. 1 Inventory trend of raw material and finished products |
由式(1)可得,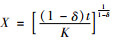
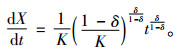
|
(2) |
在[0, tpi]时间段内,库存水平变化的状态方程为
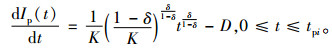
|
(3) |
根据初始条件Ip(0)=0,可得
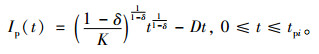
|
(4) |
在[tpi, tsi]时间段内,库存水平变化的状态方程为
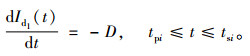
|
(5) |
根据Ip(Tpi)=Id1(Tpi),有
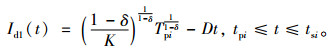
|
(6) |
进一步可得

|
(7) |
在tsi时刻将缺陷品处理掉,剩余的合格品数量为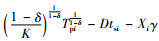
在[tsi, T]时间段内,库存水平变化的状态方程为
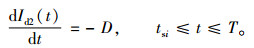
|
(8) |
根据初始条件
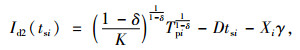
|
进一步可得
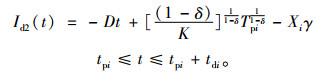
|
(9) |
根据式(6),可得第i个周期的时间长度为

|
(10) |
在[0, tpi]时间段内产成品库存成本
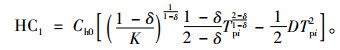
|
(11) |
在[tpi, tsi]时间段内产成品库存成本
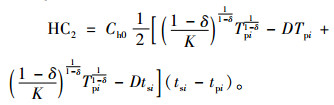
|
(12) |
在[tsi, Ti]时间段内产成品库存成本:
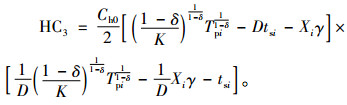
|
(13) |
原料1的存储成本为:
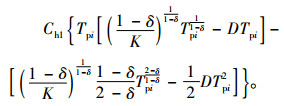
|
(14) |
所有原料的存储总成本为
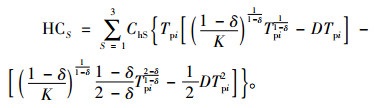
|
(15) |
在第i个周期,由于质检学习效应的存在,根据式(1)可得,质检Xi个产品的总时间为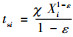
第i个周期的总成本为
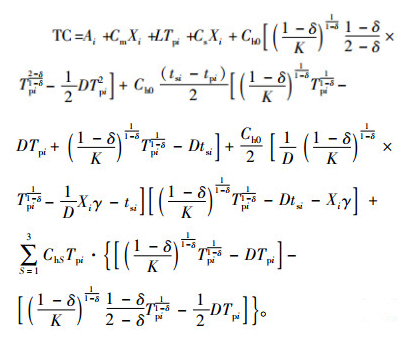
|
(16) |
第i个周期的日平均成本为
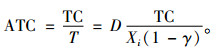
|
(17) |
将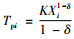
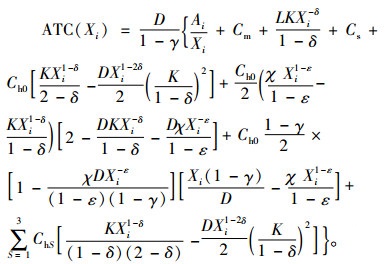
|
(18) |
对ATC(Xi)求极小值,也即求无约束的非线性规划问题。由于式(18)的高度非线性,难以求出最优解的解析表达式,因此采用数值方法求解。这里采用牛顿迭代法进行求解。牛顿法的最大优点是在方程的单根附近具有平方收敛。其中m表示牛顿迭代法的迭代次数。
令f(X)=ATC(Xi)。
求解步骤如下:
步骤1:令i=1,m=0;
步骤2:给定初始值Xi0,允许误差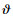
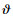
步骤3: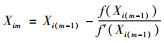
步骤4:若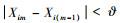
步骤5:得第1个周期最优生产量X1*=X1m。
步骤6:令i=i+1,重复步骤2~5,直到i=I(I是学习曲线稳定后的生产周期数,也就是最佳生产周期,经过测试后确定);
步骤7:得第i个周期最优生产量Xi*=Xim。
3 算例与敏感性分析生产第1个产品的时间K=0.008 d;质检第1件产品所需要的时间χ=0.023 d;生产准备费用A=200元/周期;劳动费用为L=80元/d;单位产成品的原料采购成本Cm=25元/单位;单位时间单位产成品的存储费Ch0=2.5元/d;原料1、原料2、原料3的单位时间单位存储成本Ch1=1.5元/d,Ch2=1元/d,Ch3=2元/d;单位产品的质检费用Cs=3.5元/单位;产出率学习系数为δ=0.1;质检学习系数ε=0.35;需求D=150单位/d。
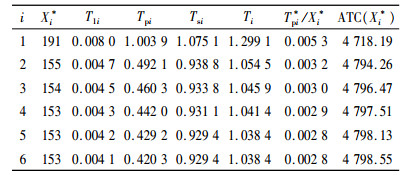
由表 1知,在生产的早期阶段,最优生产量与最优生产时间快速下降,第2个生产周期以后的学习效应表现不明显。由图 2知,随着生产周期的推进,生产单位产品的时间越来越小,但生产时间不会趋向于零,最后趋向于一个固定的值。图 2中单位产品生产时间的变化,表现出明显的学习曲线特征。
| 表 1 不同周期下的最优策略 Tab. 1 Optimal strategies under different periods |

|
图 2 周期数对单位产成品生产时间的影响 Fig. 2 Effect of cycle number on the time of production of finished products |
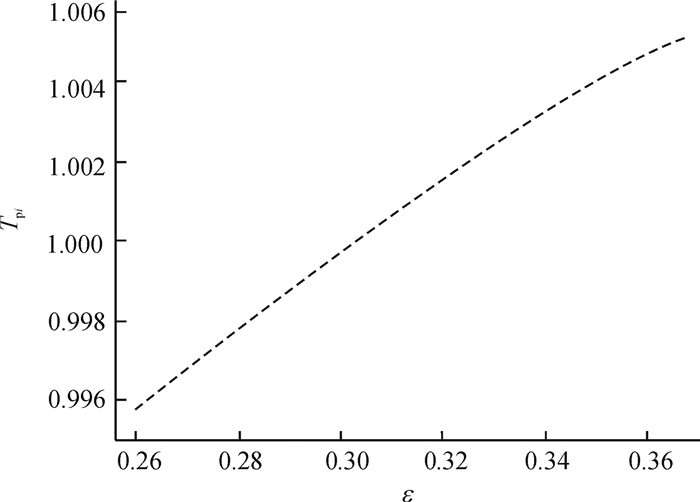
图 3反映了产出率学习系数变化对最优生产时间的影响,随着学习系数的增大,即学习率越小,因可改善的空间越来越大,所以最优的生产时间越来越小。图 4反映了质检学习系数变化对最优生产时间的影响,随着质检学习系数的增大,最优生产时间呈现出缓慢增加的趋势。

|
图 3 产出率学习系数变化对最优生产时间的影响 Fig. 3 Effect of the changing of output rate on the optimal production time |
|
图 4 质检学习系数变化对最优生产时间的影响 Fig. 4 Effect of quality control learning coefficient on optimal production time |
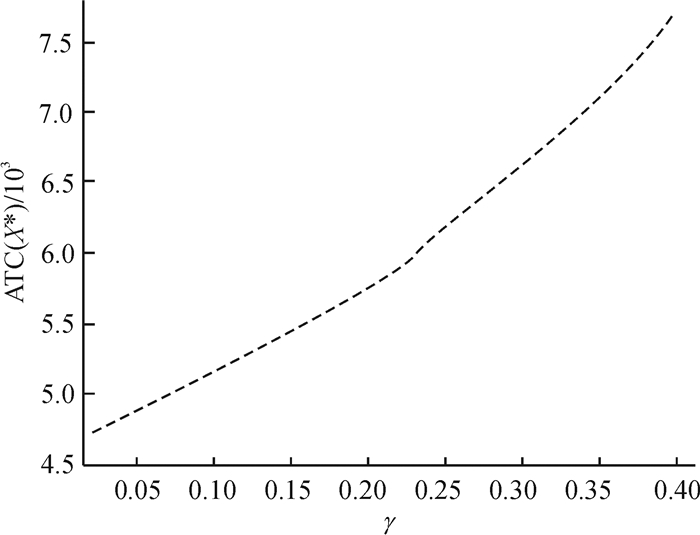
图 5反映了缺陷率对最优成本的影响,随着缺陷率的增大,制造商需要生产更多的产成品来满足消费者的需求,同时缺陷品不能出售,生产缺陷品耗费了大量的成本,故而随着缺陷率的增大,最优成本呈现快速增加的趋势。
|
图 5 缺陷率对最优成本的影响 Fig. 5 Effect of defect rate on optimal cost |
文章考虑制造商的产出率和质检过程具有学习效应的经济批量优化问题。数值分析结果表明,在早期生产阶段,学习效应对最优生产量及最优生产时间有显著的影响。在生产的后期学习效应发挥的作用有限,因为单位产品的生产时间基本保持不变,此时在学习效应上的投资是不明智的。随着缺陷率的增大,最优成本快速增加,应设法降低缺陷率。
文章的研究没有考虑生产中断带来的学习中断现象,在实际生产过程中,生产的中断,会使得学习效应带来负面影响;另外,由于产品质量学习效应的存在,产品缺陷率是越来越小的,在后续研究中,可考虑产出率同时具有学习与中断效应的情形及产品质量的学习效应。
| [1] |
WRIGHT T. Factors affecting the cost of airplanes[J].
Journal of Aeronautical Science, 1936, 3(2): 122-128.
|
| [2] |
SALAMEH M K, ABDUL-MALAK M A U, JABER M Y. Mathematical modelling of the effect of human learning in the finite production inventory model[J].
Applied mathematical modelling, 1993, 17(11): 613-615.
DOI: 10.1016/0307-904X(93)90070-W. |
| [3] |
CHEN C K, LO C C, LIAO Y X. Optimal lot size with learning consideration on an imperfect production system with allowable shortages[J].
International Journal of Production Economics, 2008, 113(1): 459-469.
DOI: 10.1016/j.ijpe.2007.03.025. |
| [4] |
MAHATA G C. A production-inventory model with imperfect production process and partial backlogging under learning considerations in fuzzy random environments[J/OL]. (2014-12-24). http://link.springer.com/article/10.1007/s10845-014-1024-2/fulltext.html.
|
| [5] |
TENG J T, LOU K R, WANG L. Optimal trade credit and lot size policies in economic production quantity models with learning curve production costs[J].
International Journal of Production Economics, 2014, 155(5): 318-323.
|
| [6] |
KHAN M, JABER M Y, WAHAB M I M. Economic order quantity model for items with imperfect quality with learning in inspection[J].
International Journal of Production Economics, 2010, 124(1): 87-96.
DOI: 10.1016/j.ijpe.2009.10.011. |
| [7] |
BALKHI Z T. The effects of learning on the optimal production lot size for deteriorating and partially backordered items with time varying demand and deterioration rates[J].
Applied Mathematical Modelling, 2003, 27(10): 763-779.
DOI: 10.1016/S0307-904X(03)00081-7. |
| [8] |
KUMAR R S, GOSWAMI A. EPQ model with learning consideration, imperfect production and partial backlogging in fuzzy random environment[J].
International Journal of Systems Science, 2015, 46(8): 1486-1497.
|
| [9] |
DAR-EL E M, AYAS K, GILAD I. A dual-phase model for the individual learning process in industrial tasks[J].
IIE transactions, 1995, 27(3): 265-271.
DOI: 10.1080/07408179508936740. |
| [10] |
JABER M Y, GLOCK C H. A learning curve for tasks with cognitive and motor elements[J].
Computers and Industrial Engineering, 2013, 64(3): 866-871.
DOI: 10.1016/j.cie.2012.12.005. |
| [11] |
JABER M Y, SAADANY A M A E. An economic production and remanufacturing model with learning effects[J].
International Journal of Production Economics, 2011, 131(1): 115-127.
DOI: 10.1016/j.ijpe.2009.04.019. |
| [12] |
SALAMEH M K, JABER M Y. Economic production quantity model for items with imperfect quality[J].
International Journal of Production Economics, 2000, 64(1): 59-64.
|
| [13] |
JABER M Y, GOYAL S K, IMRAN M. Economic production quantity model for items with imperfect quality subject to learning effects[J].
International Journal of Production Economics, 2008, 115(1): 143-150.
DOI: 10.1016/j.ijpe.2008.05.007. |
| [14] |
WAHAB M I M, JABER M Y. Short Communication: economic order quantity model for items with imperfect quality, different holding costs, and learning effects: a note[J].
Computers & Industrial Engineering, 2010, 58(1): 186-190.
|
| [15] |
MUKHOPADHYAY A, GOSWAMI A. Economic production quantity models for imperfect items with pollution costs[J].
Systems Science & Control Engineering, 2014, 2(1): 368-378.
|
| [16] |
柏庆国, 徐贤浩. 带学习效应的双渠道供应链库存策略研究[J].
中国管理科学, 2015, 23(2): 59-69.
BAI Qingguo, XU Xianhao. Study of inventory policy in a dual-channel supply chain with learning effects[J]. Chinese Journal of Management Science, 2015, 23(2): 59-69. |
| [17] |
徐健腾, 柏庆国, 张玉忠. 带学习效应的二级易变质产品供应链的最优策略研究[J].
系统工程理论与实践, 2013, 33(5): 1167-1174.
XU Jianteng, BAI Qingguo, ZHANG Yuzhong. Optimal policy for two-echelon supply chain with deteriorating items and learning effect[J]. Systems Engineering- Theory & Practice, 2013, 33(5): 1167-1174. DOI: 10.12011/1000-6788(2013)5-1167. |
| [18] |
于秀丽, 张毕西, 李逸帆, 等. 考虑员工学习效应的MOS指派优化研究[J].
工业工程, 2014, 19(1): 74-80.
YU Xiuli, ZHANG Bixi, LI Yifan, et al. Worker assignment in MOS in considering learning effect[J]. Industrial Engineering Journal, 2014, 19(1): 74-80. |
 2016, Vol. 19
2016, Vol. 19