2. 中国航空综合技术研究所 北京 100028;
3. 北京航空航天大学 可靠性与系统工程学院, 北京 100191
2. China Aero-Polytechnology Establishment, Beijing 100028, China;
3. School of Reliability and Systems Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China
波动是质量的大敌。传统的产品质量波动管理方法是运用SPC技术判定过程输出质量特性的波动是否异常,然后利用因果图、故障树等质量工具和图表,对“5M1E(人、机、料、法、环、测)”等导致质量波动的因素进行分析,形成波动源Si(i=1, 2, …,n)清单并加以改进。但对于如何将众多的波动源放在一起考虑,确定影响关系和改进优先次序,学术界和企业一直缺乏可量化的数学模型和计算方法支撑,结果是,虽然波动源分类(因果图)和逻辑关系(故障树)很清楚,但改进优先次序的选择和波动源间的层级关系很混乱。
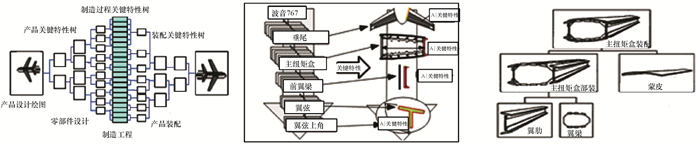
1 产品制造过程波动传递和累积模式产品制造过程的质量波动因产品结构、特性类型(如计量特性或计数特性、单一特性或多元特性等)、装配方式的不同所呈现的不同传递流程和积累模式。图 1是飞机制造过程波动沿产品结构树传递和积累的示意。
|
图 1 飞机制造过程波动沿产品结构树传递和积累示意 Fig. 1 The transmission and accumulation of process variation in aircraft manufacturing by product structure tree |
从图 1中可以看出,产品的波动沿着“系统-分系统-子系统-部件-组件-零件”的路径分解传递。在这个简化模型或路线图中,各级产品的波动具有不同的特征,对应产品关键特性的不同指标。例如,分系统级以上的波动的表征往往是可靠性指标、性能指标等;部件和组件级的波动表现为可用性、可装配性等;零件级的波动表现为零件的尺寸、形状和公差配合性等。导致零件波动的波动源不外乎“5M1E”,零件波动构成部(组)件的波动源,并沿着波动分解路径反向累积,直至产生系统级的波动。
2 产品制造过程质量波动影响关系产品制造过程的质量波动应结合过程模型来理解。在ISO 9000标准中,过程是“一组将输入转化为输出的相互关联的活动”。因此,产品制造过程的波动源分析可从4个层面开展:1)供应链层面的波动,如政治、法律、经济、产业环境等的波动;2)企业层面的波动,如资金、成本、人才等的波动;3)产品层面的波动,如产品准时交付率(OTD)、产品质量特性(如产品的功能特性、可靠性、维修性、安全性、测试性、环境适应性、保障性、经济性、舒适性、环保性等)的波动;4)制造过程层面的波动,如过程输入参数(如标准、图纸、原材料等)、操作输入和输出参数(如5M1E、进刀量、主轴转速、定位基准、测量系统、温湿度、加工尺寸等)的波动。有关文献对前3个层面的波动进行了一些研究,如下所述。
在供应链层面,Hussain等[1]基于解释结构模型和网络层次分析法,开展潜在供应商评价,分析碳税、管理培训、企业可持续发展等因素对持续稳定的供应链管理的影响和敏感性;周荣辅等[2]分析供应链质量形成的潜在影响因素和相互作用关系,提出供应链质量管理改进的建议。
在企业层面,Alidrisi[3]基于解释结构模型方法,对实施六西格玛的12个关联成功关键因素进行排序,并给出在汽车服务行业的案例;Ansari等[4]用解释结构建模技术分析了印度太阳能发电装置的13个相关障碍, 确定了1个最高层和6个最底层障碍并提出去除这些障碍的优先次序和方法;谢刚等[5]基于解释结构模型分析区域、自然资源、人均财政收入等29个梯度因素,构建五级递阶结构区域经济梯度理论模型,研究区域差异化;李卫红[6]研究制造型企业品牌竞争力的17个影响因素的关系,建立多级递阶结构模型,分析各层级关系和影响因素对品牌竞争力的作用。
在产品层面,王凤山等[7]基于工程装备质量影响因素, 构建多层递阶的质量评价体系解释结构模型;陈亚青等[8]建立航空事故的解释结构模型,将航空事故的12种原因分为4个层次的要素并分析其关联影响;林维等[9]将零件图中几何要素的尺寸及位置关系转换为要素矩阵,研究零件定位基准的选择问题;丁力平等[10]基于解析结构模型, 对产品综合关联关系进行分解, 构建和优化产品初始模块;张雷等[11]基于复杂产品零部件连接关系构建解释结构模型,研究零部件结构层次与拆卸序列规划方法;Ertas等[12]运用解释结构模型,研究基于货架产品组件的系统复杂维修性关系量化识别和诊断方法,为针对备件和主要维修工作采取预防措施提供支撑。
对于第4个层面,即制造过程层面的波动源分析,学术界主要集中在统计过程控制(SPC)、偏差流(SOV)理论等方向,研究数据驱动的分析技术,例如,汪邦军[13]研究了多元质量特性统计过程诊断与控制方法;杜世昌等[14]和Loose等[15]基于SOV理论和状态空间方程研究多阶段系统中尺寸偏差建模与控制。生产现场则大多采用因果图等定性工具来辅助分析波动原因,但由于没有形成波动原因诊断和影响因素间层级关系的多层递阶解释结构,改进优先次序选择决策的量化支撑不够。
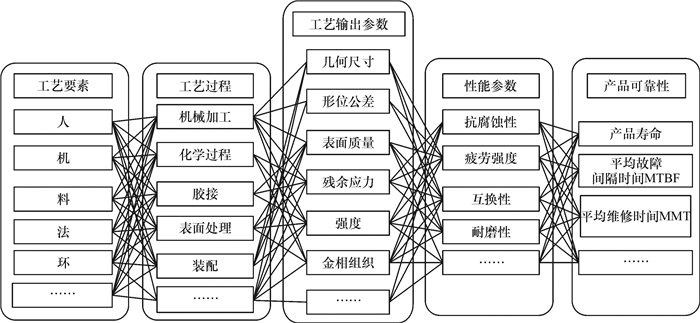
产品制造过程层面的波动原因和影响关系非常复杂, 如图 2所示。
|
图 2 产品制造过程的波动原因和影响关系 Fig. 2 The relationship between cause and effect of process variation in product manufacturing |
图 2中,产品制造过程中的工艺要素(5M1E)、工艺过程、工艺输出参数、产品性能参数、产品可靠性等涉及的要素、指标之间的影响关系构成了一个复杂的拓扑结构。图中任意一条链路,例如“方法(工艺要素)-装配(工艺过程)-表面质量(工艺输出参数)-疲劳强度(产品性能参数)-平均故障间隔时间MTBF(产品可靠性)”,既是规划和实现产品质量形成过程的工作链路,又是发现和持续改进产品质量与可靠性的工作链路。
本文认为, 产品制造过程影响关系的拓扑结构虽然非常复杂,但是在分析波动源时, 可以简化为有向图、因素集, 而经典图论中有向图又与邻接矩阵一一对应,因此, 可以运用代数的方法操作和运算, 建立波动源分析的解释结构模型进行量化分析, 支撑质量改进决策。
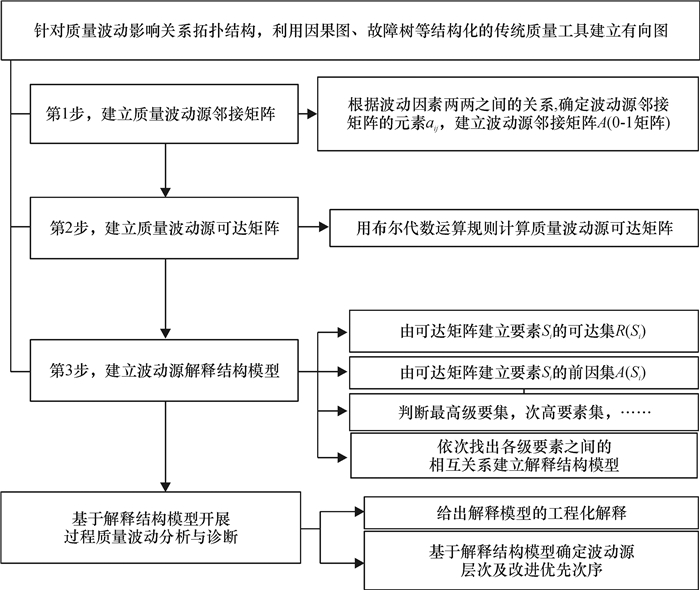
3 质量波动源解释结构模型的建模步骤产品制造过程质量波动源解释结构模型建模与分析的步骤如图 3所示。
|
图 3 产品制造过程质量波动源解释结构模型的建模与分析步骤 Fig. 3 Steps of variation source interpretative structural modeling and analysis in product manufacturing |
第1步,建立质量波动源邻接矩阵。针对质量波动影响关系拓扑结构,利用因果图、故障树等结构化的传统质量工具建立有向图,提炼质量波动因素集S={S1, S2, …,Sn}。鉴于经典图论中有向图与邻接矩阵一一对应,由有关专家与工程技术人员讨论,确定波动因素Si(i=1, 2, …, n)与Sj(j=1, 2, …, n)两两之间的关系,建立波动源邻接矩阵A,其元素aij对应不考虑循环的有向图节点之间的关系,定义如下:如果i=j,则aij=0;如果i≠j, 则
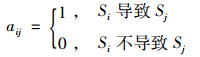
|
第2步,建立质量波动源可达矩阵。令A1=(A+I),这里,I为单位矩阵;用布尔代数运算规则(布尔加:0+0=0,1+1=1,1+0=1,0+1=1;布尔乘:0×0=0,l×1=1,1×0=0,0×1=0),计算A2=A12;以此类推,直到得到:A1≠A2≠…≠Ar-1=Ar, r≤n-1,这里n为矩阵A的阶数,则Ar-1=(A+I)=R,矩阵R是一个n阶的0-1矩阵,称为波动源可达矩阵,其元素rij非0即1,是有向图可达路径的代数表征。
第3步, 建立波动源解释结构模型。定义要素Si的可达集R(Si)={可达矩阵R的Si行中所有rij=1的列对应的要素,j=1, 2, …, n}、前因集A(Si)={可达矩阵R的Si列中所有rij=1的行对应的要素,j=1, 2, …, n};如果R(Si)A(Si),则R(Si)为多级递阶结构的最高级要素集L0;将L0各要素对应的行、列从可达矩阵R中删除,在剩下的可达矩阵中重新求得各要素的可达集、前因集、最高要素集(L1);依次类推,求得各层级(L2, L3, …)所包含的要素集;按照级间划分依次排列各要素,绘制有向图,得到波动源解释结构模型。
4 应用案例某集团第一继电器厂是某汽车配件雨刷器主要供应商。近来顾客抱怨汽车雨刷不能正常工作。经过仔细分析,发现原因主要在第一继电器厂提供的J-200型继电器上。工厂迅速作出响应,组建由质量总师亲自负责的项目小组,分析查找原因。小组运用经典SPC技术,发现问题主要归因于继电器关键部件——铁轭的尺寸波动大。为了进一步找到铁轭尺寸波动的原因,绘制铁轭制造过程因果图(图 4)。
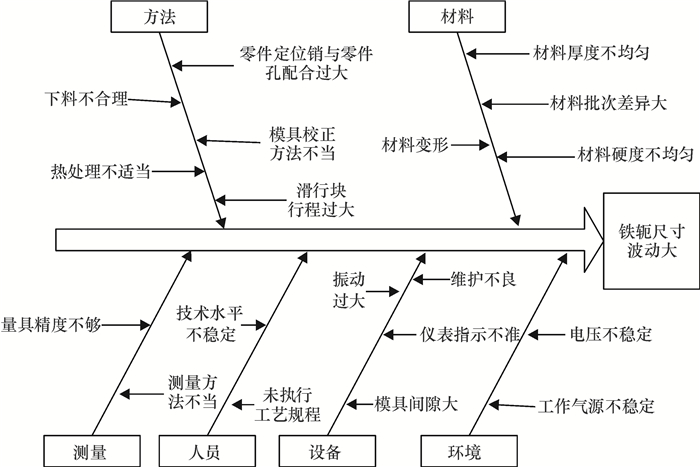
|
图 4 铁轭制造过程质量波动因果图 Fig. 4 The cause and effect diagram of quality variation in the process of iron yoke manufacturing |
为了找出铁轭尺寸波动的深层次原因,确定改进优先次序,将上述因果图中的结果因素“铁轭尺寸波动大”及其“5M1E”6个方面的19个影响因素,建立因素集如下。
S={S1=铁轭尺寸波动大;S2=下料不合理;S3=热处理不当;S4=零件定位销与零件孔配合过大;S5=模具校正方法不当;S6=滑行块形程过大;S7=材料变形;S8=材料厚度不均匀;S9=材料批次差异大;S10=材料硬度不均匀;S11=量具精度不够;S12=测量方法不当;S13=技术水平不稳定;S14=未执行工艺规程;S15=设备振动过大;S16=维护不良;S17=仪表指示不准;S18=模具间隙大;S19=电压不稳定;S20=工作气源不稳定}。
接下来,质量总师带领工作小组通过对这些因素两两之间的关系进行分析,建立邻接矩阵A如下。
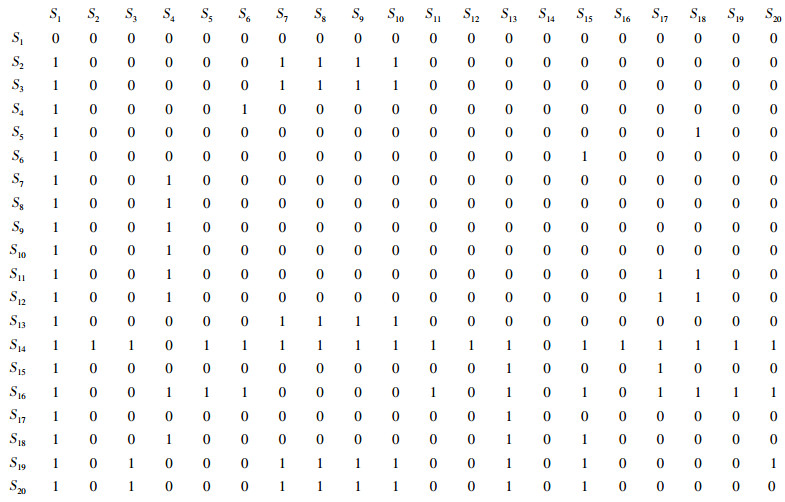
|
运用MATLAB软件,按照布尔代数运算规则,编程计算波动源可达矩阵R如下。
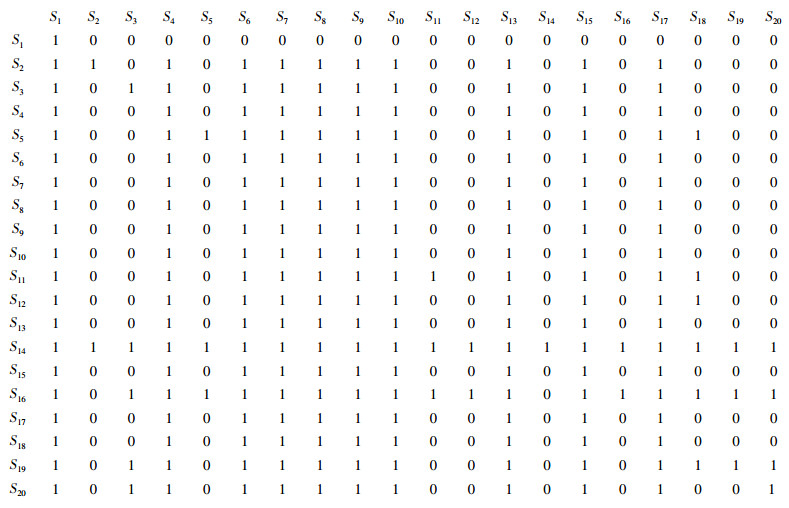
|
根据所求得的可达矩阵,逐项建立要素Si的可达集R(Si)、前因集A(Si),按照步骤3,将波动因素进行级间划分,得到最高要素集L0={S1},第1级要素集L1={S4;S6;S7;S8;S9;S10;S13;S15;S17},第2级要素集L2={S2;S3;S18;S20},第3级要素集L3={S5;S11;S12;S19},第4级要素集L4={S16},第5级要素集L5={S14}。
根据上述可达矩阵的级间划分,建立质量波动源解释结构和层次关系如图 5所示。
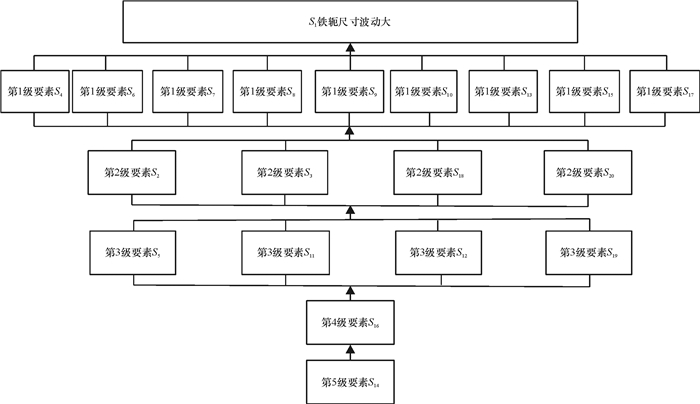
|
图 5 波动源解释结构和层次关系 Fig. 5 The structure and hierarchical relationship of variation source |
图 5实为有向图,导致铁轭尺寸波动大的波动源分为5个层次:第1层次的原因包括:S4=零件定位销与零件孔配合过大、S6=滑行块形程过大、S7=材料变形、S8=材料厚度不均匀、S9=材料批次差异大、S10=材料硬度不均匀、S13=技术水平不稳定、S15=设备振动过大、S17=仪表指示不准;第2层次的原因包括:S2=下料不合理、S3=热处理不当、S18=模具间隙大、S20=工作气源不稳定;第3层次的原因包括:S5=模具校正方法不当、S11=量具精度不够、S12=测量方法不当、S19=电压不稳定;第4层次的原因为:S16=维护不良;第5层次的原因为:S14=未执行工艺规程。
根据波动源解释结构模型和层次关系,确定改进优先次序,抓关键。1)从设备维护和工艺纪律抓起,因为这两个因素对其他因素,以及最终结果“铁轭尺寸波动”影响较大,属根本原因。2)改进第3层的波动源,包括模具校正方法不当、量具精度不够、测量方法不当、电压不稳定这一层次的原因主要是测量、计量有关的因素,改进起来较快,符合六西格玛管理等查找问题的思路,即眼睛向内,“结果”不好时先看看测量系统好不好,必要时实施测量系统分析(MSA)。3)改进第2层次的波动源,包括:下料不合理、热处理不当、模具间隙大、工作气源不稳定等,这些波动导致材料相关波动,并对最终结果有较大影响。4)改进第1层次的波动源,包括:零件定位销与零件孔配合过大、滑行块形程过大、材料变形、材料厚度不均匀、材料批次差异大、材料硬度不均匀、技术水平不稳定、设备振动过大、仪表指示不准。这一层次的波动源对最终结果有直接影响。例如,通过实施防差错装置解决零件定位销与零件孔配合过大、滑行块形程过大等问题;应用实验设计(DOE)、田口方法、响应曲面分析、稳健性设计等方法解决材料变形、材料厚度不均匀、材料批次差异大、材料硬度不均匀等问题;通过技术改造和波动管理等方法,解决技术水平不稳定、设备振动过大、仪表指示不准等问题。
5 结束语本文基于对复杂产品制造过程波动传递流程和影响因素分析,建立解释结构模型开展产品制造过程质量波动源的分层分类,确定改进优先次序,可以弥补经典SPC技术在波动控制过程中只能报警不能诊断的不足,以及因果图、故障树等传统分析工具在诊断质量问题原因时缺乏量化模型和算法支撑的不足。本文关于“复杂拓扑结构→有向图→邻接矩阵→可达矩阵→解释结构模型→工程应用”的建模方法和思路,适用于解决复杂系统的波动溯源问题,形成的工程应用案例具有一定的推广价值。
| [1] |
HUSSAIN M A, AWASTHI A, TIWARI M K. Interpretive structural modeling-analytic network process integrated framework for evaluating sustainable supply chain management alternatives[J].
Applied Mathematical Modelling, 2016, 40(5-6): 3671-3687.
DOI: 10.1016/j.apm.2015.09.018. |
| [2] |
周荣辅, 朱超博. 基于解释结构模型的供应链质量形成影响因素研究[J].
科技管理研究, 2012(7): 93-98.
ZHOU Rongfu, ZHU Chaobo. Study on factors affecting supply chain quality based on interpretative structural model[J]. Science and Technology Management Research, 2012(7): 93-98. |
| [3] |
ALIDRISI H. Prioritizing critical success factors for six sigma implementation using interpretive structural modeling[J].
American Journal of Industrial & Business Management, 2014, 4(12): 697-708.
|
| [4] |
ANSARI M F, KHARB R K, LUTHRA S, et al. Analysis of barriers to implement solar power installations in India using interpretive structural modeling technique[J].
Renewable & Sustainable Energy Reviews, 2013, 27(6): 163-174.
|
| [5] |
谢刚, 李国平. 广义梯度理论中梯度的解释结构模型研究[J].
系统工程, 2004, 22(5): 1-6.
XIE Gang, LI Guoping. An interpretive structure model on the grad in generalized-grads theory[J]. Systems Engineering, 2004, 22(5): 1-6. |
| [6] |
李卫红. 基于ISM的制造型企业品牌竞争力影响因素结构分析[J].
数学的实践与认识, 2014, 14(13): 63-71.
LI Weihong. Structural analysis of factors influencing brand competition capability in manufacturing enterprises based on interpretative structural model[J]. Mathematics in Practice and Theory, 2014, 14(13): 63-71. |
| [7] |
王凤山, 朱万红, 王全鹏. 基于ISM的工程装备质量评价体系构建方法[J].
解放军理工大学学报, 2005, 6(5): 479-483.
WANG Fengshan, ZHU Wanhong, WANG Quanpeng. Constructing quality systems of engineering equipment based on ISM[J]. Journal of PLA University of Science and Technology, 2005, 6(5): 479-483. |
| [8] |
陈亚青, 韩云祥. 解释结构模型在航空事故分析中的应用[J].
防灾科技学院学报, 2010, 30(1): 309-311.
CHEN Yaqing, HAN Yunxiang. The application of interpretive structural model to air accident analysis[J]. Journal of Institute of Disaster-Prevention Science and Technology, 2010, 30(1): 309-311. |
| [9] |
林维, 周丽莎. 基于改进解释结构模型化方法的定位基准选择[J].
计算机应用, 2010, 30(1): 309-311.
LIN Wei, ZHOU Lisha. Selection of location datum based on improved interpretative structural modeling method[J]. Journal of Computer Applications, 2010, 30(1): 309-311. |
| [10] |
丁力平, 谭建荣, 冯毅雄, 等. 基于解析结构模型的产品模块构建及其优化[J].
计算机集成制造系统, 2008, 14(06): 1070-1077.
DING Liping, TAN Jianrong, FENG Yixiong, et al. Construction of product module based on interpretive structure modeling and its optimization[J]. Computer Integrated Manufacturing Systems, 2008, 14(06): 1070-1077. |
| [11] |
张雷, 刘志峰, 杨明, 等. 基于解释结构模型的产品零部件拆卸序列规划[J].
计算机辅助设计与图形学学报, 2011, 23(4): 267-275.
ZHANG Lei, LIU Zhifeng, YANG Ming, et al. Disassembly sequence planning based on interpretative structural mode[J]. Journal of Computer Aided Design & Computer Graphics, 2011, 23(4): 267-275. |
| [12] |
ERTAS A, SMITH M W, TATE D, et al. Complexity of system maintainability analysis based on the interpretive structural modeling methodology: transdisciplinary approach[J].
Journal of Systems Science & Systems Engineering, 2016, 25(2): 254-268.
|
| [13] |
汪邦军. 多特性工业过程质量诊断与控制[J].
航空标准化与质量, 2006(1): 14-18.
WANG Bangjun. Multivariate statistical process diagnosis & control[J]. Aeronautic Standardization & Quality, 2006(1): 14-18. |
| [14] |
杜世昌, 奚立峰, 潘尔顺. 多阶段系统中尺寸偏差建模与控制[J].
上海交通大学学报, 2006, 40(4): 583-587.
DU Shichang, XI Lifeng, PAN Ershun. Modeling and controlling of dimensional variation in multi-stage manufacturing system[J]. Journal of Shanghai Jiao Tong University, 2006, 40(4): 583-587. |
| [15] |
LOOSE J P, ZHOU Q, ZHOU S, CEGLAREK D. Integrating GD&T into dimensional variation models for multistage machining processes[J].
International Journal of Production Research, 2010, 48(11): 3129-3149.
DOI: 10.1080/00207540802691366. |
 2016, Vol. 19
2016, Vol. 19