《中国低碳经济发展报告(2015)》称:2016年起中国将建立全国统一碳市场,这将成为全球最大的碳排放权交易市场。环境污染和全球气候变暖已成为国际社会高度关注的问题。如何控制温室气体排放,减缓全球气候变暖已成为世界政治、经济、能源、环境等领域的重要议题[1]。近来各企业都在寻找减少碳排放量的途径,大量实践证明通过对批量和订货量的调整,碳排放量都能在一定程度上实现减少。这导致了企业对碳排放量(包括二氧化碳排放量及其他温室气体的排放)的高度重视。在不断重视环保责任感的消费群体及政府相关部门的影响下,企业都在努力减少运营中的碳排放足迹。
近年来,考虑碳排放的EOQ问题的研究越来越多。Wahab等[2]研究了使供应商总成本最小的运输和生产决策问题,结果表明如果考虑环境的影响,产品运输的次数就会减少。Bonney等[3]的研究结果表明与传统的EOQ的模型相比,增加每次订货的数量和减少订货的次数会有利于订货成本和碳排放量。随着绿色可持续库存管理问题的关注度上升,大多学者在研究相关问题时会考虑碳限制、碳交易等影响。Hua等[4]研究了企业考虑碳排放上限与交易机制时的库存管理中的碳排放足迹问题,推导出了产品的最优订货量,并与传统的EOQ模型进行对比分析碳交易、碳单价及碳税对最优订货量、碳排放量、总成本的影响。Letmathe等[5]研究了碳排放限额与碳排放权交易机制下企业产品组合和数量的线性规划和混合整数规划最优化模型。Rosic等[6]基于报童模型建立了一个考虑碳排放成本的单周期模型,分析了碳排放因素对订购量的影响。Chen等[7]探讨了以严格碳排放限额为约束条件的EOQ模型,给出了通过调整订购量可以减少碳排放的条件。曾伟等[8]针对生产供应商和采购商构成的两级供应链系统,基于需求为一固定常数的联合经济批量(JELS)模型,对碳限额与交易机制下供应链优化进行建模分析。夏海洋等[9]研究了随机需求下运输成本依赖于订货量和提前期的提前期可控的生产库存联合优化模型。上述研究都是将碳排放量作为限制因素研究单目标优化问题,而且大多是将需求设定为一个已知的常数或者随机变量。本文假定需求是一个与零售价格和碳排放量相关的函数,同时考虑碳排放最小化和制造商利润最大化的多目标订货决策优化问题。
本文在传统EOQ问题的基础上,考虑了一个与零售价格和碳排放量相关的需求函数,每次订货时,运输产生的碳排放量与订货次数呈线性关系,库存产生的碳排放量与库存量呈线性关系,采用加权求和的方法求解碳排放最小化和制造商利润最大化的多目标订货决策问题。
1 模型描述与构建 1.1 问题描述在运输和库存产品的过程中需要消耗大量的能源,这会导致产生大量的碳排放,因此,本文主要考虑由运输和库存活动产生的碳排放量。
1.2 符号说明与假设D表示市场需求,与单位产品的零售价格和碳排放量相关;Q表示制造商每次接受的订货批量,为决策变量;hm表示制造商单位时间持有单位库存的成本,s表示制造商每次启动生产的成本,c表示制造商单位产品的生产成本,w表示制造商单位产品的售价。g0表示产品库存的固定碳排放量, g表示与平均库存量相关的单位可变碳排放量, e0表示可变碳排放量, e表示空车时的碳排放量。α表示最大的市场需求,即终端客户需求;β表示价格弹性;θ表示消费者低碳偏好系数,其中α>0, β>0, θ>0。CF表示碳排放量, t表示单位碳排放量缴纳的碳税。
不失一般性,假设模型满足:
1) 消费者对零售商的产品需求受碳排放量的影响,消费者更喜欢购买绿色产品,同时,碳排放量每增加一个单位,消费者对其需求减少θ个单位;
2) 运输条件在考虑碳税机制前后都是保持不变的,只需要考虑运营决策;
3) 制造商单位产品的售价w高于生产成本c,其中订货批量Q是决策变量。
1.3 单目标决策模型在计算碳排放量时,为了简化问题,本文考虑每次订货时,运输产生的碳排放量与订货次数呈线性关系,库存产生的碳排放量与库存量呈线性关系。根据上述假设,供应链系统的运输产生的碳排放量表示为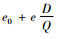
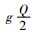
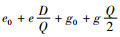
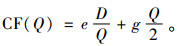
|
(1) |
假设制造商的需求函数取决于零售价格和碳排放量,目前这种需求函数公式被一些环保企业和零售商广泛使用,如:法国卡斯诺(Casino)公司以及英国乐购(Tesco)[10]。设需求函数表达式为
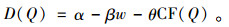
|
将式(1)代入需求函数表达式得到
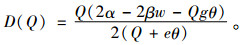
|
(2) |
制造商的利润函数表达式为
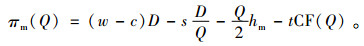
|
(3) |
分别求出利润最大化订货量QM*和碳排放量最小化订货量QE*的表达式为
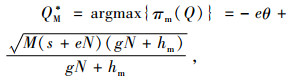
|
(4) |
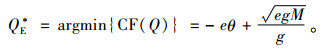
|
(5) |
其中M=2α-2βw+egθ2, N=t-cθ+wθ, M、N均大于0。
命题1 当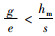
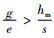
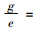
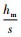
证明 对式(4)、(5)的差值求解,有QM*-QE*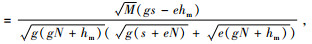
所以有
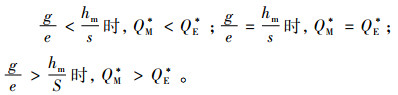
|
证毕。
由命题1可以发现,单位库存产生的碳排放量、每次运输产生的碳排放量、订货成本以及库存成本之间的关系会影响制造商最优订货量的决策。库存产生的碳排放一般与库存方式、地址等选择有关,产生较低碳排放的库存方式往往需要投入更多的库存成本,物流过程中产生的碳排放量与交通工具的选择、燃料的选择以及运输距离有关[11]。比如燃油价格的增加会提高订货成本,节能交通工具的选择会减少运输过程的碳排放量。很明显,将式(4)、(5)得到的最优订货量代入式(1)、(3),可知最优值满足不等式πm(QM*)≥πm(QE*), CF(QM*)≥CF(QE*), 说明使得制造商利润最大化的订货批量常常是不能保证碳排放量也是最小的。从式(4)、(5)的表达式可以看出,最优订货量的值不仅与库存成本、碳排放水平有关,还与消费者低碳偏好系数有关。
碳税的变化对碳排放量最小化时的订货量QE*没有影响,但是碳税对利润最大化时的订货量QM*有影响,这符合实际。因为制造商在追求碳排放量最小化时,无论政府对其征收多少税收,产品的生产都不会有所变化。因此下面将以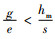
命题2 在利润最大化条件下,制造商利润随着碳税的增加而下降。
证明 对于πm(QM*)的表达式,关于碳税t进行求偏导,计算化简得到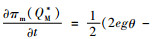
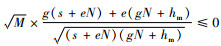
证毕。
由命题2可以发现,因为制造商在只考虑利润最大化的情况下,政府征税必然会导致制造商的成本增加,从而降低制造商的利润。这也说明对于只考虑利益而不考虑生产过程是否会不利于环境保护的制造商而言,政府采取征收碳税的政策可以有效惩罚这些企业,引起他们对环境的保护意识。
命题3 在利润最大化条件下,制造商最优订货量随着碳税的增加而增加。
证明 通过对QM*关于碳税t求偏导,得到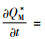
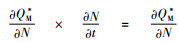
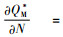
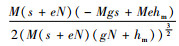
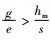
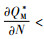
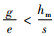

由命题4可以发现,制造商只考虑自身利益时,政府增加碳排放的税收会使制造商每次的订货量更大,这可能是因为制造商为节约运输成本,减少运输次数,增加运货量来达到减排减税的目的。
命题4 在利润最大化条件下,制造商的需求随着碳税的增加而增加。
证明 对D(QM*)关于碳税t求偏导,得到
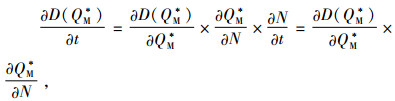
|
对于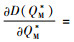
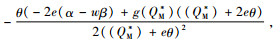
当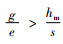
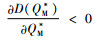



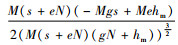
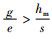
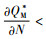
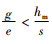

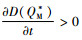
由命题4可以发现,政府增加碳排放量的税收会导致制造商所生产的产品需求增加,由命题1知,碳税增加会导致制造商的利润降低,制造商一方面为了获得更多的利润,另一方面为了满足消费者对低碳产品的需求,就会通过改进生产技术等方式生产更多的低碳产品,因为制造商在碳排放量一定时,与普通产品相比可以生产更多的低碳产品。碳税的增加也会减少制造商的碳排放,由需求函数也可以知道,碳排放的下降会导致需求的增加。
命题5 在利润最大化条件下,制造商产生的碳排放量随着碳税的增加而降低。
证明 对CF(QM*)关于碳税t求偏导,得到
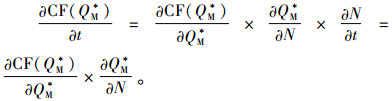
|
对于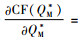
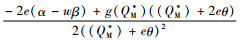
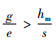

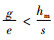

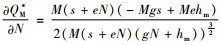
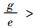
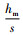
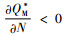
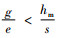
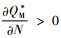
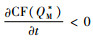
由命题5可以发现,政府征收碳税能有效的激励制造商降低碳排放量,制造商为了避免因缴纳过多的碳税导致成本过高,通常会生产低碳替代品或者利用技术改进来者控制碳排放量。
综上命题发现碳税政策会降低碳排放量,有利于环境保护,还会促进消费者需求的增长,但是会有损制造商获得的利润。
1.4 多目标决策模型在同时考虑碳排放量最小化和利润最大化时,本文通过隶属度函数将不同的目标统一成无量纲的隶属度单目标函数进行求解[12-13],将多目标规划模型转换为单目标规划模型。首先对式(1)和式(4)两个目标函数分别建立隶属函数,然后对隶属函数加入隶属度的计算权重λ,得到新的目标函数为
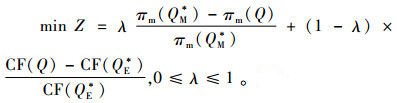
|
(6) |
命题6 在同时考虑碳排放量最小化和利润最大化时,多目标隶属函数Z存在极小值。
证明 通过对Z关于订货量Q求导,得到
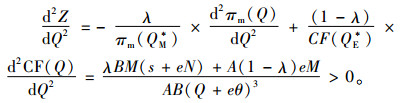
|
所以新的目标函数(6)一定存在最优解。令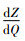
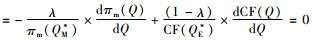
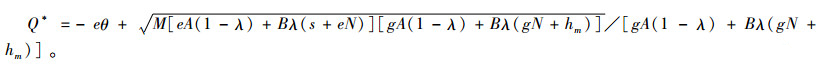
|
(7) |
其中,πm(QM*)=A, CF(QE*)=B, 且A、B均大于0。当λ=0时,有Q*=QE*;当λ=1时,有Q*=QM*。通过比较式(4)、(5)、(7)可知QE* < Q* < QM*。
命题7 在同时考虑碳排放量最小化和利润最大化时,制造商利润随着碳税的增加而减少。
证明 通过对πm(Q*)关于碳税t求偏导,得到
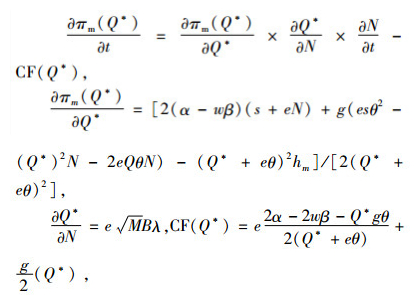
|
所以


证毕。
由命题7可以发现,制造商在同时考虑利润最大化和碳排放最小化的情况下,碳税对制造商利润的影响与命题2中制造商只考虑利润最大化时的影响相同,此时,政府增加对碳排放量的税收会使得制造商的利润降低。这可能是因为随着政府对单位碳排放量征收的税增加,制造商为了减少纳税就会采用环保的方式进行生产运营,比如选择节能环保的燃料和交通工具,通过技术改进减少生产产品的碳排放量等,而这些减排的措施会增加部分成本,且增加的这部分成本高于因为碳减排节省的碳税,导致制造商的最终利润下降。
命题8 在同时考虑碳排放量最小化和利润最大化时,订货量在0 < λ < λ*范围内随着碳税的增加而减少,在1>λ>λ*范围内随着碳税的增加而增加。
证明 通过对关于碳税t求偏导,得到
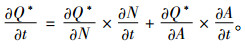
|
因为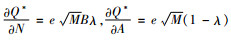
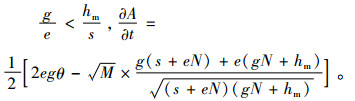
|
所以
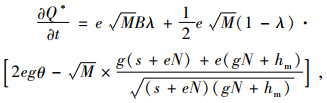
|
继续求出
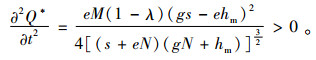
|
令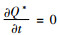
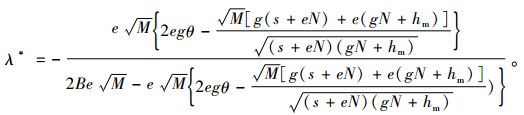
|
所以当0 < λ < λ*时,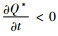
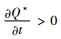
由命题8可以发现,政府的税收政策对订货量的影响与命题3的结论也不一样,取决于制造商对利润和碳排放量的权重。当利润的权重小于λ*时,即制造商重视所生产的产品对环境的影响,碳税的增加会降低订货量;当利润的权重大于λ*时,即制造商重视经济利益, 碳税的增加会提高订货量,因为碳税的提高增加了制造商的碳排放成本,为了追求更大的利润,制造商会通过增加每次的订货量,减少运输次数来减低运输成本。
命题9 在同时考虑碳排放量最小化和利润最大化时,需求在0 < λ < λ*随着碳税的增加而减少,在1>λ>λ*范围内随着碳税的增加而增加。
证明 通过对D(Q*)关于碳税t求偏导,得到: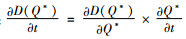


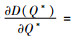
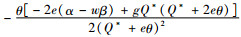
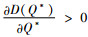

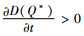
由命题9可以发现,政府的税收政策对需求的影响与命题8中一致,即随着企业追求的目标不同,政府的税收政策对市场需求的变化会产生不一样的效果。
命题10 在同时考虑碳排放量最小化和利润最大化时,碳排放量在0 < λ < λ*范围内随着碳税的增加而增加,在1>λ>λ*范围内随着碳税的增加而减少。
证明 通过对CF(Q*)关于碳税t求偏导,得到: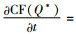
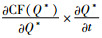
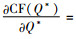
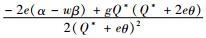
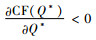

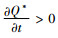
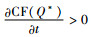
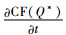
由命题9可以发现,当0 < λ < λ*,即制造商对碳排放量相当重视时,政府增加碳排放的税收会取得适得其反的效果,这可能是因为企业在降低碳排放量时需要投入更多的资本,而增加的碳税会使制造商丧失更多的利润,导致企业进行技术改进的资金投入减少,所以产品的碳排放量反而会增加;当1>λ>λ*, 即制造商主要以利润最大化为导向进行决策时,政府的税收政策能够有效地促进企业减少碳排放量,制造商会进行技术创新等措施降低碳排放量,以此向潜在客户树立良好的绿色环保形象
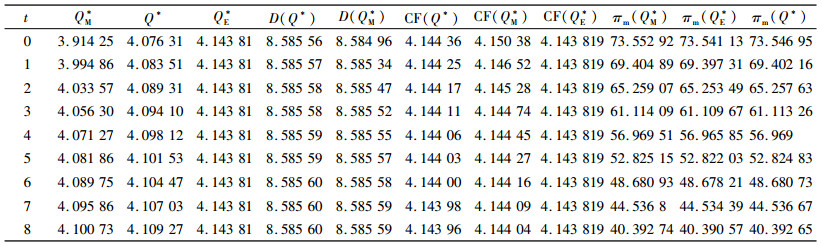
2 算例分析为了验证模型和命题的正确性及实用性,现参考文献[14]中的数据, 对模型进行验证。假设α=10, β=0.1, θ=0.1, e=1, g=1, w=10, c=1, hm=1, s=0.8, 该参数设置满足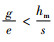
| 表 1 不同碳税下各决策的比较(λ=0.8) Tab. 1 Comparison of optimal decisions under different carbon tax |
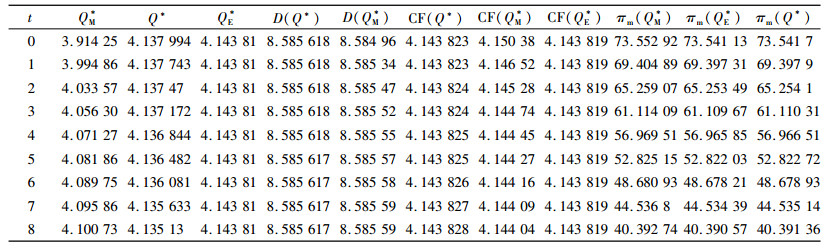
| 表 2 不同碳税下各决策的比较(λ=0.2) Tab. 2 Comparison of optimal decisions under different carbon tax |
由表 1的数据可以看出,无论碳税为多少,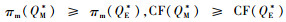
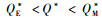
随着碳税的增加,无论是单目标决策还是多目标决策,制造商的利润都是呈下降趋势,这验证了命题2和命题7的正确性。这也说明了企业在面对政府征税的压力下,因为增加了减排的技术成本,使得利润降低。对于企业而言,如果技术方面投入的资金较多,可以考虑在运输过程中减少碳排放,比如选择节能环保的燃料和交通工具。
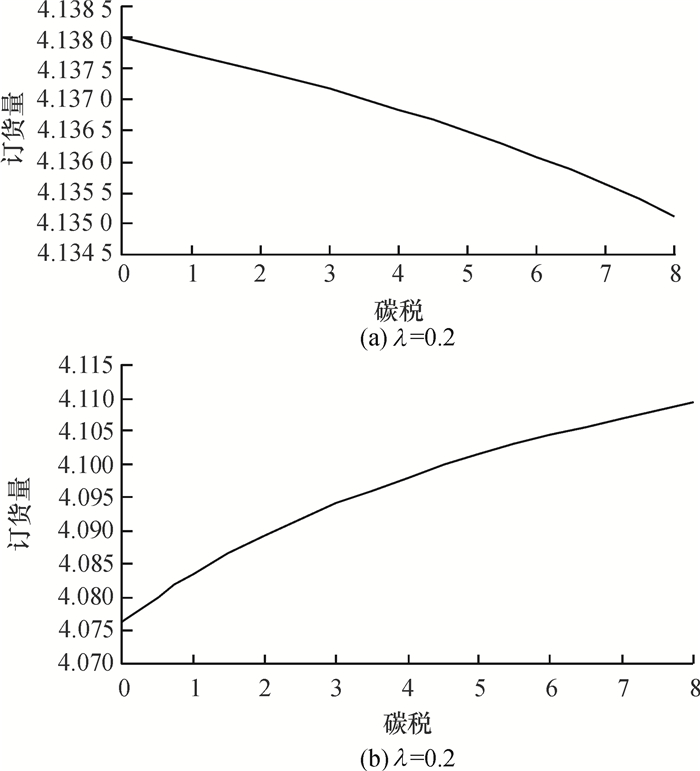
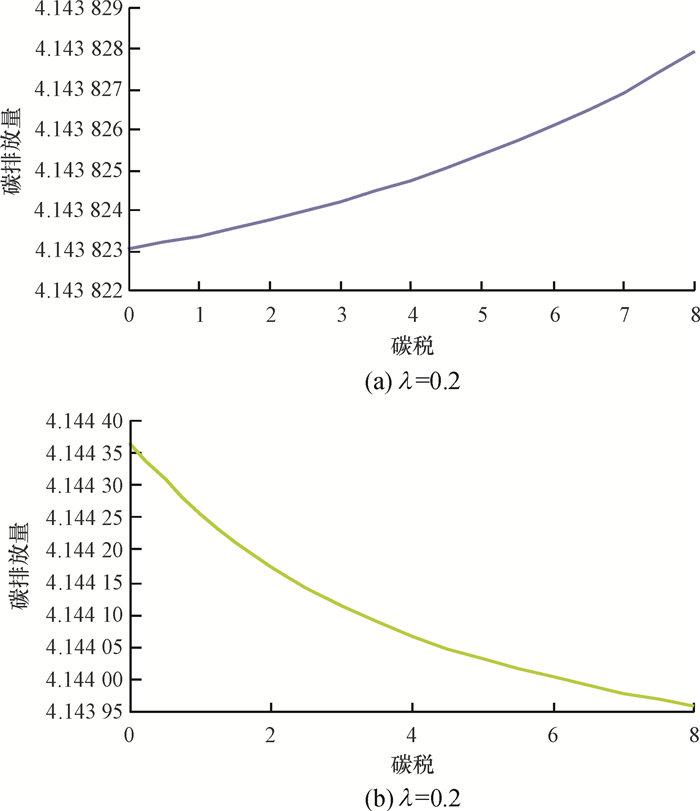
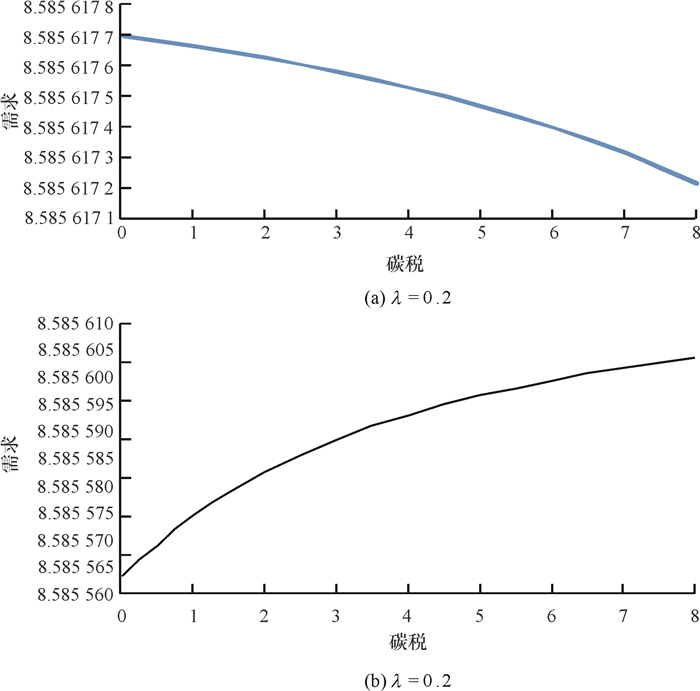
由图 1~图 3可知, 在同时考虑碳排放量最小化和利润最大化时,随着碳税的增加,不同隶属度权重下的订货量、需求和碳排放量均呈现出不一样的变化趋势。对于重视环境污染的企业(0 < λ < λ*,算例中取λ=0.2),市场需求随着碳税的提高而降低,碳排放量反而增多,说明对于环保意识强的企业,政府增加碳税会起到适得其反的效果,这可能是因为企业在降低碳排放量时需要投入更多的资本,而增加碳税会使制造商丧失更多的利润,导致企业进行技术改进的资金投入减少,所以产品的碳排放量反而会增加, 对于这种企业政府应该采取降低碳税的政策;对于重视经济利益的企业(1>λ>λ*,算例中取λ=0.8), 碳税的增加会提高订货量,降低碳排放量,因为碳税的提高增加了制造商的碳排放成本,为了追求更大的利润,制造商会努力减少运输成本,即可以通过增加每次的订货量,减少运输次数来减低运输成本,同时这也会减少运输过程的碳排放量。这说明对于大多数追求经济利益的企业,政府应该增加碳税来减少碳排放量。此外,政府也可以辅以财税补贴政策或者差异化标准的碳税政策来鼓励他们节能减排,以此减少环境污染。
|
图 1 不同隶属权重下碳税对订货量的影响 Fig. 1 The effect of carbon taxon orders under different weight of membership |
|
图 2 不同隶属权重下碳税对需求的影响 Fig. 2 The effect of carbon tax on demands under different weight of membership |
|
图 3 不同隶属权重下碳税对碳排放量的影响 Fig. 3 The effect of carbon tax on carbon emissionsunder different weight of membership |
本文基于传统的EOQ模型,研究碳排放最小化和制造商利润最大化条件下的多目标订货决策模型。模型中制造商的碳排放量并不是单纯的与订货量呈线性关系,而是考虑每次订货时,运输产生的碳排放量与订货次数呈线性关系,库存产生的碳排放量与库存量呈线性关系。采用加权求和的多目标规划解法,分析了碳税对多目标决策的影响,发现不同隶属度权重下,碳税对多目标决策的订货量、需求和碳排放量的影响也不一样,即对于环保意识强的企业,政府应该采取降低碳税的政策;对于重视经济利益的企业,政府应该增加碳税来减少碳排放量。
本文可以为政府减低碳排放提供参考,对于环保意识高的企业应该降低碳税,对于那些以利益为导向的企业应该增加碳税。以后可以继续研究随机需求下多目标规划订货决策,还可以将本文只研究单个制造商的情况延伸到供应链系统中。
| [1] |
国务院发展研究中心课题组. 全球温室气体减排:理论框架和解决方案[J].
经济研究, 2009(3): 4-13.
Project Team of Development Research Center of the State Council of China. Greenhouse gas emissions reduction:a theoretical frame work and global solution[J]. Economic Research, 2009(3): 4-13. |
| [2] |
WAHAB M I M, MAMUN S M H, ONGKUNARUK P. EOQ models for a coordinated two-level international supply chain considering imperfect items and environ-mental impact[J].
International Journal of Production Economics, 2011, 134(1): 151-158.
DOI: 10.1016/j.ijpe.2011.06.008. |
| [3] |
BONNEY M, JABER M Y. Environmentally responsible inventory models: non-classical models for a non-classical era[J].
International Journal of Production Economics, 2011, 133(1): 43-53.
DOI: 10.1016/j.ijpe.2009.10.033. |
| [4] |
HUA G, CHENG T C E, WANG S. Managing carbon footprints in inventory management[J].
International Journal of Production Economics, 2011, 132(2): 178-185.
DOI: 10.1016/j.ijpe.2011.03.024. |
| [5] |
LETMATHE P, BALAKRISHNAN N. Environmental considerations on the optimal product mix[J].
European Journal of Operational Research, 2005, 167(2): 398-412.
DOI: 10.1016/j.ejor.2004.04.025. |
| [6] |
ROSIC H, BAUER G, JAMMERNEGG W. A framework for economic and environmental sustainability and resilience of supply chains//rapid modelling for increasing competitiveness tools and mindset[M]. London: Springer, 2009:91-104.
|
| [7] |
CHEN X, BENJAAFARS, ELOMRI A. The carbon-constrained EOQ[J].
Operations Research Letters, 2013, 41(2): 172-179.
DOI: 10.1016/j.orl.2012.12.003. |
| [8] |
曾伟, 王瑶池, 周洪涛. 碳限额与交易机制下供应链运作优化研究[J].
管理工程学报, 2015, 29(3): 199-206.
ZENG Wei, WANG Yaochi, ZHOU Hongtao. Study on supply chain operations optimizationunder carbon cap and trade mechanism[J]. Jonrnal of Industrial Engineering, 2015, 29(3): 199-206. |
| [9] |
夏海洋, 黄培清. 随机需求下提前期可控的生产一库存联合优化模型[J].
控制与决策, 2008, 23(6): 631-636.
XIA Haiyang, HUANG Peiqing. Integrated production-inventory model with stochastic demand and controllable leadtime[J]. Control and Decision, 2008, 23(6): 631-636. |
| [10] |
UPHAM P, DENDLER L, BLEDA M. Carbon labeling of grocery products: public perceptions and potential emissions reductions[J].
Clean. Prod, 2011, 19(4): 348-365.
DOI: 10.1016/j.jclepro.2010.05.014. |
| [11] |
HUA G, CHENG T C E, WANG S. Managing carbon footprints in inventory management[J].
International Journal of Production Economics, 2011, 132(2): 178-185.
DOI: 10.1016/j.ijpe.2011.03.024. |
| [12] |
CHEN C L, YUAN T W, LEE W C. Multi-criteria fuzzy optimization for locating warehouses and distribution centers in a supply chain network[J].
Journal of the Chinese Institute of Chemical Engineers, 2007, 38(5-6): 393-407.
DOI: 10.1016/j.jcice.2007.08.001. |
| [13] |
刘金明. 基于多目标规划的城市道路交叉口信号配时研究[D]. 北京: 北京交通大学, 2011.
LIU Jinming. On signal timing of the urban road intersections based on multi-objective programming[D]. Beijing: Beijing Jiaotong University, 2011. |
| [14] |
HOVELAQUE V, BIRONNEAU L. The carbon-constrained EOQ model with carbon emission dependent demand[J].
International Journal of Production Economics, 2015, 164: 285-291.
DOI: 10.1016/j.ijpe.2014.11.022. |
 2016, Vol. 19
2016, Vol. 19