2. 华中科技大学 经济学院,湖北 武汉 430074;
3. 北京振冲工程股份有限公司,北京 100102;
4. 宾西法尼亚州立大学 能源与矿产工程系,美国宾夕法尼亚州大学城,16802
2. School of Economics, Huazhong University of Science and Technology, Wuhan 430074, China;
3. Beijing Vibroflotation Engineering CO., LTD., Beijing 100102, China;
4. Department of Energy and Mineral Engineering, Pennsylvania State University Park, PA, US, 16802
工程风险管理一般包括风险识别、风险分析、风险应对和监控四个过程,其中风险分析为风险应对提供决策依据,是风险管理的难点[1-2]。有效的风险应对决策必须理解风险事件之间的因果作用关系而不仅仅是相关关系,虽然人们开发了大量的风险分析与建模方法[3-4],但它们中绝大部分无法量化处理风险事件间因果作用,从而无法为风险应对提供有力支撑[4-6]。
因果贝叶斯网络(causal Bayesian network,CBN)是一种结合了概率论和图论的数学模型,可定量刻画风险事件之间的因果关系,同时能够有效地进行多源信息融合,在风险分析中获得广泛应用[7-9]。CBN主要应用局限是在结构建模过程中,风险事件有多种分类结果,各分类间因果关系难于明确;因果关系主要依赖专家判断,受到专家个人的知识与经验的严重影响,容易“因果早熟”(为结果迅速寻找一个原因,但往往不是结果的真正原因);参数建模同样严重依赖专家判断,工作量巨大;多专家概率判断集成困难等,这些问题阻碍了CBN网络在实际风险分析中的应用[9-11]。
王爱文等[12]提出了一种基于因果贝叶斯网络的风险建模与分析(risk modeling and analysis based on casual Bayesian network, CBN-based RMA)方法,采用基于业务的流程分析和结构化的专家判断抽取和集成尝试解决这些问题。CBN-based RMA首先进行作业流程分析识别出可能出现的风险事件,然后按时间顺序分析风险事件之间的因果关系,构建因果贝叶斯网络模型,利用贝叶斯吐真剂(Bayesian truth serum, BTS)方法降低专家判断中的过度自信和动机偏差[13],确定模型参数,最后识别出关键的风险事件以便于风险应对决策。该方法提供一种结构化、流程化,且可验证的分析技术,有利于实现风险分析的持续改进。
本文改进了CBN-based RMA方法,引入4种常见模式简化其结构建模,可显著降低参数建模中专家判断工作量,提高了方法的可操作性,并通过一个巴基斯坦Neelum-Jhelum水电站隧洞掘进工程(简称NJ)风险管理案例,展示该方法的应用,验证了该方法的有效性。
1 模型与方法 1.1 风险识别与分类风险识别是CBN-based RMA的第一步,一般采用流程图法、专家调查法和专家深度访谈相结合的方法进行风险识别:首先分析业务流程,画出业务流程图,然后,针对业务流程图中的工作,识别工作要求及目标,采用专家调查法,专家填写风险因素清单(针对不能达成工作要求或目标),征求各位专家判断每项风险因素的影响程度和发生的概率,得到初步风险识别调查结果,在此基础上,通过专家深度访谈进行风险归类,剔除一些不重要的和级别较低的风险,合并一些相似的风险因素,得到最终风险清单。
风险归类是风险管理不可或缺的基础性工作,其目的是便于风险的识别和对不同类型的风险采取不同的分析方法和管理措施。改进的CBN-based RMA方法针对项目管理层次和职能进行归类,确保每一个风险因素都能找到负责人,任何无法找到负责人的风险因素都需要进一步细化分析,并利用责任分配矩阵方法明确相关干系人的风险责任,提高风险控制效率。
1.2 因果风险分析模型结构建模为了构造风险事件因果分析模型,首先要确定各节点和节点之间的因果关系。上一阶段识别的各个风险因素,可认为是因果贝叶斯网络中的各个节点;根据业务流程图,结合专家意见,可以确定各个风险因素(节点)之间的因果关系。
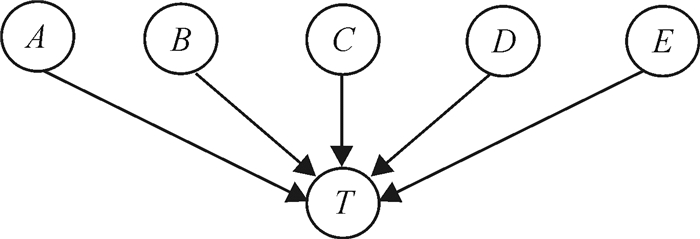
在识别风险事件之间的因果关系过程中,虽然具体情况千差万别,但大致可归纳为四种模式,分别为因果型模式、度量型模式、集成型模式和归纳型模式[9],其中,集成型模式是一种亟需简化的结构形式,这种模式表示了一种“多因一果”的关系,如图 1所示。
|
图 1 集成型模式 Fig. 1 Synthesis Idiom |
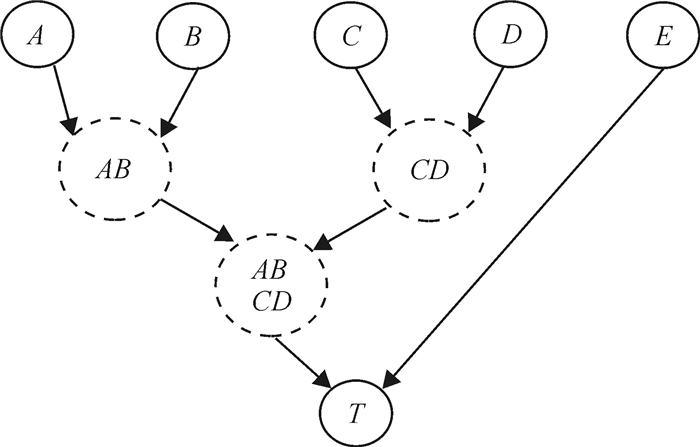
在图 1中,风险因素A、B、C、D、E均为T的父节点,假设每个节点存在3种状态,则对T来说需要估计(3-1)×35=486个参数。如果换成图 2的形式,同样假设每个节点存在3种状态,对于条件概率P(AB|A, B),需要估计(3-1)×32=18个参数,同理P(CD|C, D), P(ABCD|AB, CD), P(T|ABCD, E), 也各仅需要估计18个参数,这样该模型总共需要估计18+18+18+18=72个参数,估算工作量显著降低了,特别是需要利用专家进行主观判断的时候,这种方法更凸显出其优势。
|
图 2 简化后的贝叶斯网络 Fig. 2 Simplified Bayesian network |
为了确定贝叶斯网络参数,往往需要对专家进行第二轮调研,获得各风险因素的先验概率分布(对于根节点)或给定父节点下的条件概率分布。
为了保证数据的科学有效性,可能需要对专家判断中的明显冲突和矛盾之处咨询专家意见,调整一些偏差比较大的数据。
最终得到的数据一般采用线性意见池(linear opinion pool)方法[14]集成专家判断,得出每个节点的先验概率分布或条件概率分布。
例如,对于先验分布,可以按照如下公式进行集成:
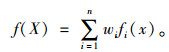
|
(1) |
其中,X代表特定问题的参数; n代表专家的数量; fi(x)代表第i个专家的判断; wi代表第i个专家所具有的权重; f(X)代表集成后的概率分布。
当参数建模完成之后,构建了一个基于因果贝叶斯网络的风险分析模型。
1.4 风险事件因果作用和敏感性分析针对该因果分析模型,可以通过贝叶斯网络的概率推理以及“do”操作和“后门规则”等分析一个风险因素对另外一个风险因素的因果作用[7],不但可用于描述风险传导效应,还可为未来风险责任分摊提供量化依据。
该模型同时允许对风险因素进行敏感性分析,以识别敏感度高的关键风险因素,有针对性地制定相应控制措施。敏感性分析一方面有助于简化不必要的风险控制程序,另一方面可以协助规划风险控制成本,对于风险管理决策起到很大的帮助。
2 NJ案例分析为了验证模型和方法的有效性,本文以BVE公司所承接的巴基斯坦Neelum-Jhelum水电站引水隧洞工程(NJ工程)为例,从施工方的角度进行详细分析。
2.1 NJ项目基本情况NJ工程位于巴基斯坦Azad Jammu & Kashmir州,为长隧洞引水式水电站。引水隧洞总长28.6 km(单线洞和双线洞交错布置),共设置5条施工支洞(分别为A1~A5),其中A1、A2支洞间的引水隧洞长13 577 m,是本工程的关键线路和施工难点,在此段引水隧洞采用TBM(全断面隧洞掘进机)进行掘进施工。TBM施工段沿线地质条件复杂,具有埋深大、洞线长的特点,存在高压外水、泥页岩遇水软化及膨胀、高埋深洞段大收敛变形、涌(突)水、围岩稳定性差及隧洞穿越断层破碎带等主要工程地质问题。
该项目为BVE公司承接的第一个国际TBM工程,除项目本身较大的技术和管理风险以外,还面临着政治、经济形势、政策等风险,这些风险因素错综复杂,为了保证盈利还要保证工期,迫切需要一个描述风险因素间作用关系的分析模型,并在此基础上进行有效的风险管理,最终公司选择CBN-based RMA方法进行风险建模。
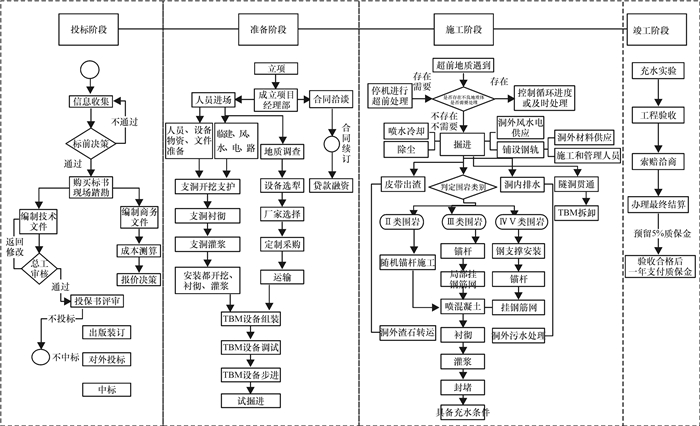
2.2 风险识别和分类 2.2.1 NJ项目生产流程分析分析项目生产流程是进行风险识别的重要环节,NJ项目的流程图如图 3所示。
|
图 3 NJ项目TBM业务流程 Fig. 3 TBM business process diagram of NJ project |
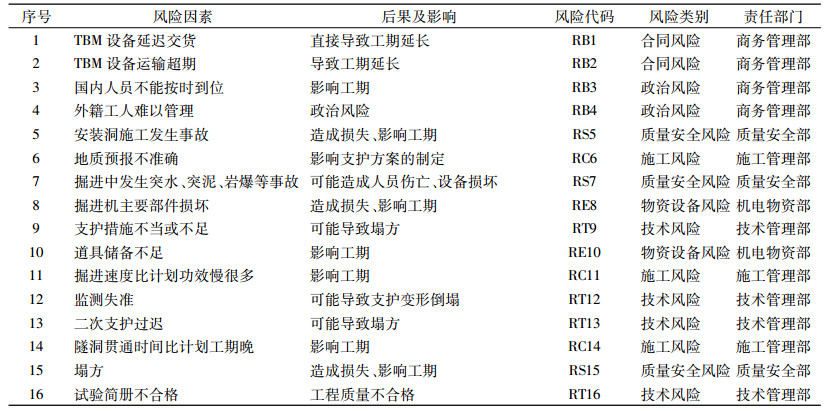
为了正确识别风险,采用两轮工作。首先根据TBM工程特点和历史数据,设计了调查问卷,发放到公司及TBM项目各位专家,发放30份,回收17份,汇总统计后共辨识出56项风险,形成第一轮TBM工程风险识别调查结果。然后,根据项目组织架构及风险可管理性,与几位资深TBM工程项目管理和技术专家进行了几轮专家深度访谈,访谈的结果剔除了一些不重要和级别比较低的风险,合并了一些相似的风险因素,整理出一份16个风险因素的风险清单,并确定风险控制责任部门,如表 1所示。
| 表 1 NJ项目风险因素分类 Tab. 1 Risk factor classification of NJ project |
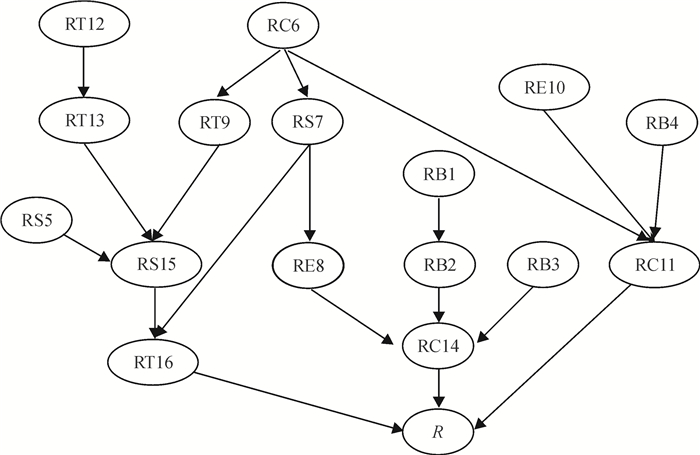
本文采用问卷调查和专家深度访谈相结合的方法确定NJ项目风险因素的因果关系,得到初步的因果贝叶斯网,由于初始因果贝叶斯网中存在较为复杂的集成型模式,按照1.2节所述的贝叶斯网简化方法,对初始因果贝叶斯网进行简化,简化后的结果见图 4。
|
图 4 NJ项目的风险影响图 Fig. 4 Risk influence diagram of NJ project |
其中,节点R为项目总风险,即项目的按要求竣工的风险。
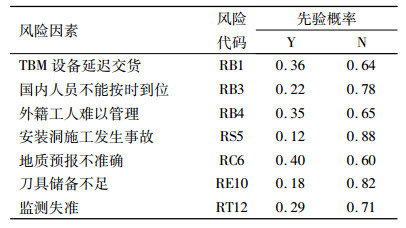
确定了因果关系后,还需要确定每个父节点的先验概率以及子节点的条件概率。先验概率和条件概率的获得同样采取了问卷调查和专家深度访谈相结合的方法,在得到多个专家的判断意见后,利用线性意见池的方法对专家判断进行集成。由于都是绝大部分是施工方专家且同在一家公司,因此假设他们的判断没有动机偏差。最终得到的父节点先验概率结果见表 2,条件概率表见表 3。
| 表 2 父节点先验概率分布 Tab. 2 Prior probability distribution of parent nodes |
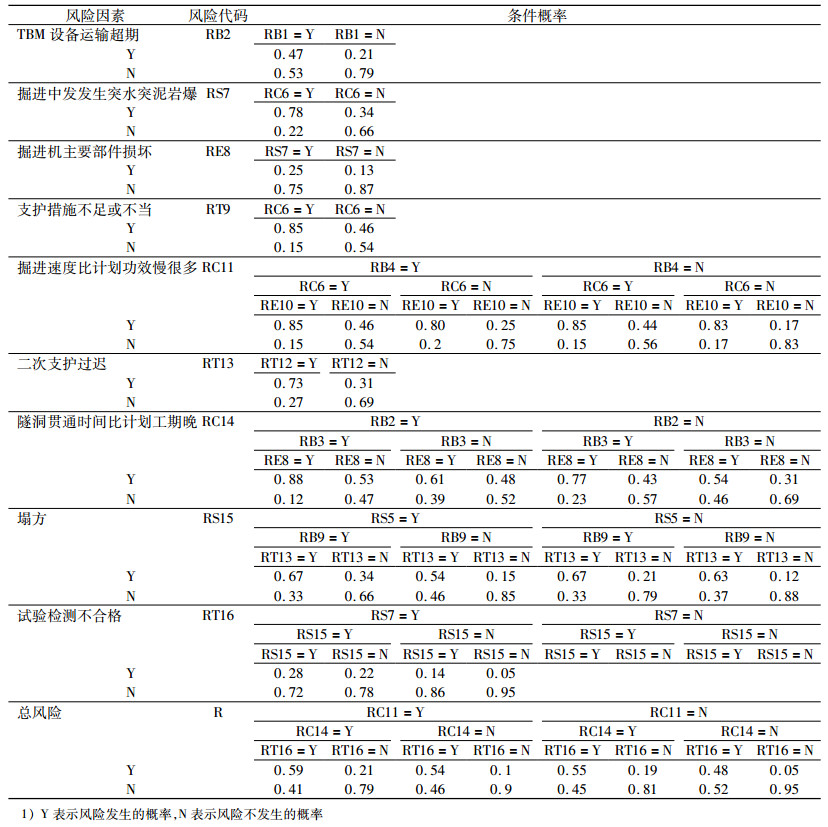
| 表 3 NJ项目条件概率1) Tab. 3 Conditional probability table of NJ project |
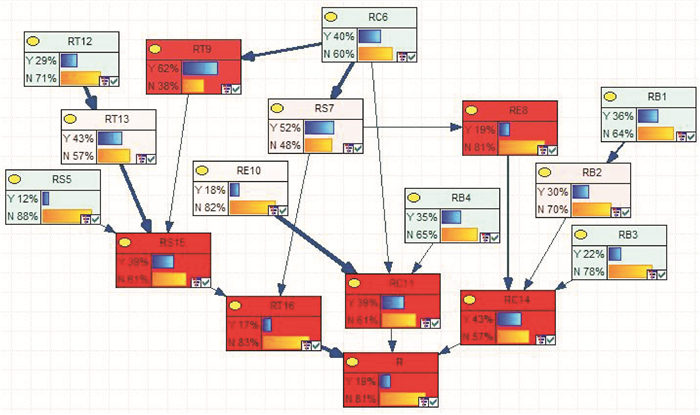
在确定因果贝叶斯网的结构和参数后,采用GeNIe软件可以计算出总风险R发生的概率为19%,见图 5。
|
图 5 NJ项目中风险影响的贝叶斯网络模型 Fig. 5 Bayesian network model for risk influence in NJ project |
在图 5中连接线粗细程度不一样,连接线越粗,表示影响程度越大,反之,连接线越细,表示影响程度越小。比如,RS5、RT9、RT13 3个因素同时都可能导致RS15的发生,但3个因素对RS15的影响程度不同,RT13对RS15的影响最大。
2.3.2 敏感性分析贝叶斯网络建成后,还需对风险因素进行敏感性分析,通过敏感性分析找到关键风险因素。
利用GeNIe对其进行敏感性分析,如图 5所示。
根据敏感性分析的结果,颜色越深说明敏感性越高,越浅则敏感性越低。在图 5中,RE8、RT9、RC11、RC14、RS15、RT16为敏感性最高的风险因素,也是首先要关注的关键风险因素;RB2、RS7、RE10、RT13为敏感性次高的风险因素;RB1、RB3、RB4、RS5、RC6、RT12为非关键风险因素。
2.4 风险监控与应对风险种类的不同,所采用的应对措施也不尽相同,根据图 5指出的关键风险因素,其应对措施如表 4所示。
| 表 4 NJ项目风险应对措施 Tab. 4 Risk responses in NJ project |
NJ项目具备一般TBM工程项目所具备的风险高、工艺复杂等特点,在NJ项目风险评估中使用CBN-based RMA方法,利用业务流程图,结合专家意见,能够较准确地识别出风险因素,确定风险因素之间的关系,并按照部门职能对这些风险进行分类,可以确定每个风险因素所对应的责任部门,为风险应对和监控提供依据,另外应用贝叶斯网络对项目进行风险分析,充分考虑风险因素之间的关系,能够提高分析的精度和有效性,可清晰识别出关键风险因素,根据风险因素之间的相互关系以及风险分类过程所确定的责任部门,可针对性地制定应对措施和监控方案,相对于其他风险管理方法,风险控制效果显著。
NJ项目已于2014年10月完工,目前还在整理资料和最终结算、索赔阶段,从现在情况看,NJ项目风险控制良好,盈利显著超过预期,业主也非常满意。
CBN-based RMA为TBM工程的风险管理提供了一种可参考的管理思路,在该案例应用也存在一些挑战,如由于样本量和历史数据有限,数据主要通过专家判断的方式获取,主观性偏强;因TBM工程风险比较复杂,因果关系的确定是一个难题;调查问卷被访者全部来自施工方,视角不够全面等,需要进一步改进。
4 总结本文改进了CBN-based RMA方法,在风险分类、模型构建、专家概率判断集成等方面提高了该方法的可操作性,同时,通过在一个实际工程项目中的应用,验证了该方法的有效性。
在应用过程中,发现专家选择对风险建模分析具有重要影响,不同专家的视角不同,风险认知不同,在构建模型时有较大冲突,案例统一采用施工方视角,存在局限性。此外,因果关系也需要一个明确的界定,否则不同的人理解有很大不同,这些值得进一步研究。
| [1] |
PMI. A guide to the project management body of knowledge[S]. (Fifth Edition) USA: Project Management Institute, 2013.
|
| [2] |
CONROW E H. Effective risk management: Some keys to success[M].UK:Aiaa, 2003.
|
| [3] |
ISO/IEC. 31010:2009-Risk management-Risk assessment techniques[M]. USA: American National Standards Instit, 2009.
|
| [4] |
COX L A. Risk analysis of complex and uncertain systems[M]. New York: Springer, 2009.
|
| [5] |
HUBBARD D W. The failure of risk management: why it's broken and how to fix it[M]. New Jersey: John Wiley & Sons, Inc., 2009.
|
| [6] |
CABANO S L. Do we truly understand project risk?[J].
Engineering Management Review, IEEE, 2005, 33(1): 19-19.
DOI: 10.1109/EMR.2005.25173. |
| [7] |
PEARL J. Causality: models, reasoning and inference[M]. 2nd ed. New York: Cambridge University Press, 2009.
|
| [8] |
王双成, 唐海燕, 刘喜华. 用于风险管理的贝叶斯网络学习[J].
控制与决策, 2007, 22(5): 569-572.
WANG Shuangcheng, TANG Haiyan, LIU Xihua. Learning bayesian networks in risk management[J]. Control and Decision, 2007, 22(5): 569-572. |
| [9] |
FENTON N, NEIL M. Risk assessment and decision analysis with Bayesian networks[M]. USA: CRC Press, 2012.
|
| [10] |
O'HAGAN A, OAKLEY J E. Probability is perfect, but we can't elicit it perfectly[J].
Reliability Engineering & System Safety, 2004, 85(1): 239-248.
|
| [11] |
HORA S C. Eliciting Probabilities from Experts[M]//EDWARDS W, RALPH F. MILES J, WINTERFELDT D V. Advances in decision analysis: from foundations to applications. New York; Cambridge University Press, 2007: 129-153.
|
| [12] |
王爱文, 杨敏, 段华蕾. 基于因果贝叶斯网络的风险建模与分析[J].
系统工程与电子技术, 2013, 35(5): 1023-1030.
WANG Aiwen, YANG Min, DUAN Hualei. Risk modeling and analysis based on casual Bayesian network[J]. Systems Engineering and Electronics, 2013, 35(5): 1023-1030. |
| [13] |
PRELEC D. A Bayesian Truth Serum for Subjective Data[J].
Science, 2004, 306(5695): 462-466.
DOI: 10.1126/science.1102081. |
| [14] |
CLEMEN R T, WINKLER R L. Combining probability distributions from experts in risk analysis[J].
Risk Analysis, 1999, 19(2): 187-203.
|
 2016, Vol. 19
2016, Vol. 19