我国制造业正处于转型的关键时期,研发是转型升级过程中最有效的助力剂,为此我国政府和企业高度重视并积极支持创新型的技术研发项目,投入了大量资源。企业研发项目立项的门槛相对较低,一般在前期论证时只要具备某些重要方面的特征,便可以立项。但是高投入并不等于高成功率,近年来对研发项目的有关统计数据,显示出居高不下的项目失败率,同时也表明了中止决策在项目过程管理中的重要性[1]。
项目中止决策是对正处于研发过程中的项目,根据其进展中表现出的内外部特征(例如技术、市场、组织及经济等方面的特征),采用一定方法对项目前景进行推断,以决定项目是否继续执行、中止或暂缓执行的一类决策活动。中止决策是对研发过程的监督和控制,是对立项项目的后评估[2]。当项目进展到一定阶段后,内外环境的不确定性有所降低,拥有的信息量更多也更为可靠,有利于对项目前景作出客观、准确的判断,中止决策后留下的项目成功率更高。
识别影响项目成功的主要因素、建立合理的决策指标体系是中止决策的前提和基础。研发环境的复杂性使得其主要因素逐渐由“硬”变“软”,市场需求状况、市场竞争状况、与企业的战略匹配程度等非技术因素的重要作用日益突出[3]。项目在此方面的发展状况需要决策者进行测评,具有一定的主观性,单纯依靠决策者的经验知识定义边界参数、对新项目进行评判取舍的决策方法存在严重缺陷。此时如果能找到若干有典型代表性、已有定论的项目作为案例项目,从其资料数据中提取所需的决策知识,再结合决策者的经验判断较为可靠。下文在介绍案例环境下中止决策模型背景的基础上,针对该问题多属性分类决策的本质特点以及评价信息的不确定性,提出一种结合模糊灰靶模型的研发项目中止决策方法。
1 项目中止决策问题与模型背景企业在技术创新过程中,由于内外界环境的变动、自身力量不足及创新经费的有限性,必须将一部分未达到预期目标的项目予以中止,以确保其他项目顺利进行。多项目的中止决策问题,是技术管理部门对进展到一定阶段的一组研发项目的“群体淘汰赛”,是企业进行统一调控资源、改善资源配置的有效途径。文献[4]根据项目的具体情况,从战略匹配性、技术可行性、顾客接受情况、市场机会与财务业绩5个维度建立了中止决策指标体系。文献[5]使用云决策模型处理项目的评价信息,得到项目的综合云,通过对比各项目综合云与参考云的期望、熵的位置判别项目的运行状况,进而决定项目是继续、暂缓还是中止。综合云能够直观地反映项目的整体发展水平,但在与参考云进行对比判断时缺乏明确标准。文献[6]在案例环境下,利用物元模型和可拓集理论,构建反映项目中止决策特点的关联函数和可拓评判模型,得到案例项目与待判项目的综合值,再依照待判项目综合值对应区间项目做出决策。当案例项目数量充足时,该方法能够明确待判项目的类型,否则难以达到预期效果(如图 1所示)。

|
图 1 案例数量不足导致无法判定待判项目类别 Fig. 1 Unable to determine the categories of the projects due to insufficient cases |
上述情况表明,仅以项目综合值为依据无法完成对所有待判项目的决策,需要通过案例分析获得更多的决策参数。本文在项目综合值的基础上,通过案例分析提取一种用以区分项目的类间指标——分类临界点,无论案例项目数量多寡,不会存在一些待判项目无法确定其类型情况。将问题的模型背景描述如下。
现有案例项目集{Pj1, Pj2, …, Pjm}与进展到一定阶段的若干项目{Pjm+1, Pjm+2, …, Pjs},需要在综合多方因素和系统分析的基础上,作出待判项目是继续执行、暂缓执行还是中止的决策。项目管理部门根据其规划目标与阶段特征,建立了包含{B1, B2, …, Bn}共n个指标的中止决策指标体系。案例项目的结果已有定论,各指标的属性值从以往记录与数据资料中分析得出,待判项目的指标属性值需要组织专家进行测评,记aij为项目Pji(i=1, 2, …, s)相应于指标Bj(j=1, 2, …, n)的属性值。先从案例项目{Pj1, Pj2, …Pjm}的信息中提取必要的决策知识与分类参数,以此为基础对待判项目{Pjm+1, Pjm+2, …, Pjs}进行决策。
2 项目中止决策的灰靶分析模型 2.1 模糊评估标度决策者在测度项目属性时,由于存在数据资料不完整、知识经验局限、思维认识模糊以及项目发展状况不确定等情况,采用模糊标度比李克特量表更切合实际[7]。三角模糊数与梯形模糊数都是最常用的模糊集,梯形模糊数的表达形式更具普适性而为本文所采用。
定义1 隶属度为fA :R→[0, 1]的模糊数称之为梯形模糊数,fA具有如下形式。
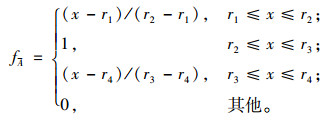
|
(1) |
其中, -∞ < r1≤r2≤r3≤r4 < +∞,可以将梯形模糊数A简要表示为A=(r1, r2, r3, r4),r2=r3时梯形模糊数便转化为三角模糊数,梯形模糊数的运算法则及距离公式在文献[8]中已有详细介绍。以梯形模糊数定义为基础,本研究选用粒度为9的评价术语集[9],各术语及其所对应梯形模糊数如表 1所示。
| 表 1 基于梯形模糊数的评价术语集 Tab. 1 Relationship between the trapezoidal fuzzy numbers the degrees of linguistic importance |
灰靶决策是灰色系统理论的重要组成部分,体现了“目标可接近、方案可完善、途径可优化”的灰色系统理论思想。决策中定义方案在属性上的上、下临界值作为满意效果的所在区域,当存在多个可能方案时,通过引入先验知识、补充信息等方法确定一个或若干个满意解。本文根据项目中止决策问题特点,依托灰靶决策的框架体系,提出一种结合模糊灰靶决策的项目分类决策方法。
正、负靶心是灰靶决策中的标杆,在项目指标属性为评价值的情况下,通常将上、下限临界值构成的向量作为正、负靶心[10]。设z+={z1+, z2+, …, zn+}、z-={z1-, z2-, …, zn-}分别为灰靶决策的正、负靶心,指标权重向量为ω+={ω1+, ω2+, …, ωn+},di+与di-为项目Pji与正、负靶心之间的距离,通过以下公式计算。

|
(2) |

|
(3) |
其中, d(aij, zj+)、d(aij, zj-)分别为项目Pji的第j指标的属性值aij与正靶心zj+、负靶心zj-之间的距离,使用梯形模糊数的距离公式[8]计算得出。通过di+与di-计算各项目的综合靶心距di为

|
(4) |
di兼顾正靶心距di+与负靶心距di-,且0≤di≤1。di数值越大项目离负靶心的距离越远,表明综合评估结果越好,数值越小则反之。
对于具有若干个待判项目的分类决策问题,仅获得项目的综合靶心距无法判定其所属类别,此时需要更多的分类参数。鉴于待判项目被分为继续执行、中止和暂缓3类,正靶心与负靶心之间应有2个分类临界点、3个分类区间,如图 2所示。将临界点1与临界点2的值分别表示为h1与h2,分类规则如下。

|
图 2 基于综合靶心距的项目分类 Fig. 2 Determining the categories of the projects based on target-center distance |
1) 当项目的综合靶心距di∈[0, h1)时,为中止项目;
2) 当项目的综合靶心距di∈[h1, h2),为暂缓项目;
3) 当项目的综合靶心距di∈[h2, 1],为继续执行项目。
由于决策中存在许多模糊性因素,使用精确数值界定项目类别,不能很好地诠释分类结果的合理性。这里将综合靶心距所属的分类区间模糊化处理(如图 3所示),设μk(di)为综合靶心距di所属第k(k=1, 2, 3)类分类区间的隶属度函数,μk(di)同样为梯形模糊数形式。

|
(5) |

|
(6) |

|
(7) |
参数q(0≤q≤1)为分类区间的模糊度,取值越大模糊度越高,反之则模糊度越低,可以先根据实际情况设定(例如先设定为0.05),再由大向小试算确定。μk(di)反映了项目i相应于第k分类区间的隶属程度,μk(di)的值越接近于1,di属于第k类区间的程度越高;反之越接近于0,属于第k类区间的程度越低,μk(di), k=1, 2, 3的函数形式如图 3所示。

|
图 3 模糊分类区间的隶属度函数 Fig. 3 The membership function of the fuzzy intervals |
基于案例分析的项目分类过程实际上是从案例项目的指标信息中提取权重ω=(ω1, ω2, …, ωn)和靶心距分类临界点h1、h2,在满足一定前提条件下,各案例项目相应于所属分类区间的隶属度越大,说明属性权重ω与项目分类临界点h1、h2设置较为合理。首先,分类临界点h1、h2的取值必须符合分类区间的要求;其次,属性权重要满足归一化条件;最后,由于属性权重对于项目分类结果有着直接影响,尽管决策者难以确定其精确值,也可以根据相关资料和经验提供部分先验知识,在分类中应予以考虑。不完全属性权重知识可以使用下面一组线性不等式描述。

|
(8) |
综合以上分析,建立基于案例的属性权重ω与项目分类临界点h1、h2设置的最优化模型,在满足h1、h2与ω所在区间约束的前提下,使得所有案例项目的隶属度函数值中的最小值达到最大化。

|

|
(9) |
最优化模型(9)目标函数中的μk(di),使用式(5)~(7)计算获得。该模型的可行域为非空凸集,因此必存在最优解。由于模型的变量规模有限,使用MATLAB优化工具箱便可以方便地求解。提取分类参数h1、h2与权重向量ω以后,对于有待分类的新项目,利用式(2)~(4)计算获得项目的综合靶心距,最后根据综合靶心距所在的分类区间判断其类别,进而做出继续执行、暂缓或中止的决策。
3 案例研究国内某知名制造企业的在研项目中,有4项正处于概念开发的完成阶段。从产品开发早期对项目进行跟踪管理,预警或中止缺乏良好前景、造成资源浪费的项目是非常必要的。根据项目管理部门的规划目标与项目运行阶段的特点,结合市场、环境、技术水平、资源状况、组织结构等多方面因素,制定中止决策指标体系为:B1(市场需求状况),B2(与产业和资源政策的一致性),B3(项目实际投资超过预算程度),B4(产品技术创新能力),B5(与企业战略的一致性),B6(开发进度与计划要求的符合情况),B7(风险估计)。该企业技术管理部门邀请业内专家对在研项目的各项属性值进行了评估,并结合以往已有定论的9个案例项目的资料数据进行决策分析。将案例项目与待判项目的指标属性值列于表 2,其中, “S1”表示继续执行项目; “S2”表示暂缓执行项目;“S3”表示中止项目,“#”表示待判项目。
| 表 2 项目属性值与项目类别 Tab. 2 The decision attributes and the categories of the projects |
按照上文所提方法设置灰靶决策的正靶心z+={h8, h8, …, h8}与负靶心z-={h1, h1, …, h1},再使用梯形模糊数的距离公式计算样本项目i=1, …, 9的各属性值与正、负靶心的距离d(aij, z+)、d(aij, z-),将结果列于表 3。
| 表 3 正、负靶心距 Tab. 3 The positive and negative target-center distance |
决策者对于属性权重有一定的先验知识。根据以往的信息资料,将不完全的权重知识整理为

|
将上述权重约束与式(6)、式(7)、式(9)相结合,建立属性权重ω与分类临界点h1、h2设置的最优化模型,模型中的q取值为0.05。使用MATLAB优化工具箱求解模型,获得属性权重ω为

|
分类临界点与各项目的综合靶心距的计算结果如图 4所示。

|
图 4 分类临界点与综合靶心矩 Fig. 4 The sorting threshold with the target center distance |
图 4中,样本项目1与样本项目7的综合靶心距没有严格符合分类临界点的划分标准。以样本项目1为例,其综合靶心距d1=0.573,如果没有采用模糊隶属度的处理方法,d1必须大于分类临界点h2的值。考虑到评估标度的模糊性和决策者主观判断的不确定性,有必要允许h2在一定范围变动,变动范围q=0.05,此时案例项目1属于分类区间S1的隶属度函数值为0.82,属于合理结果。将q取值适当减小,q=0.03时运行模型,属性权重和分类参数并没有变化,只是项目1与项目7的隶属度函数值有所增加,q的取值依赖于决策者对于分类参数模糊程度的认可范围。利用上述步骤获得的属性权重,将待判项目的属性值代入式(2)~(4),计算待判项目的综合靶心距分别为

|
将上述计算结果结合分类临界点参数值表明,Pj10和Pj11的综合靶心距位于第3类区间,属于继续执行项目;Pj12的综合靶心距位于第1类区间,属于中止项目;Pj13的综合靶心距则位于第2类区间,为暂缓执行项目。
上述方法能够通过对案例的分析提取足够的分类信息,无论待判项目数量多少,都可以明确其所属类别。但是如果没有确定分类临界点,仅以项目的综合靶心距(即综合效用值)为依据,可能出现无法判定项目类别的情况。以上述结果为例,如果按照综合靶心距对所有案例项目与待判项目进行排序,从大到小依次为

|
根据待判项目综合靶心距所在区间,可以明确Pj10、Pj11与Pj12的类别。以Pj11为例说明,其综合靶心距的取值介于案例项目Pj3与Pj1的综合靶心距的取值之间,容易判定其类别与Pj3、Pj1同为继续执行项目。但是对于待判项目Pj13,其综合靶心距的取值介于案例项目Pj5与案例项目Pj1之间。由于这两个样本项目不属于同一类别,无法判定项目Pj13所属类别究竟是与项目Pj5还是与项目Pj1一致。本文所提方法通过建立优化模型,不仅计算出决策属性权重值,还获得了用以确定项目类别的分类临界点,能够方便地对所有待判项目进行分类决策。
4 结论中止决策是研发项目过程管理中的重要问题,而目前国内外研究对此关注较少。根据该问题模糊多属性分类决策的本质,本文以案例分析为起点,结合模糊集与灰靶决策理论构建优化模型,提出了基于区间模糊数的靶心距及分类区间隶属度计算方法,从样本项目信息中提取属性权重、分类临界点等决策分类知识。无论案例项目数量多寡,都可以实现对待判项目的分类决策。该模型设计合理,意义明确,对于企业解决实际问题有一定参考价值。
| [1] |
STEFFENS W, MARTINSUO M, ARTTO K. Change decisions in product development project[J].
International Journal of Project Management, 2007, 25(7): 702-713.
DOI: 10.1016/j.ijproman.2007.01.008. |
| [2] |
FRANCISCO-JOSE M C, JOSE-LUIS M A. New product performance indicators: time horizon and importance attributed by management[J].
Technovation, 2009, 29(10): 714-724.
DOI: 10.1016/j.technovation.2008.11.005. |
| [3] |
MUAMMER O. Factors which influence decision making in new product evaluation[J].
European Journal of Operational Research, 2005, 163(3): 784-801.
|
| [4] |
PILAR C F, JOSE-LUIS M-A, ANAL I R Z. Criteria employed for go/no-go decisions when developing successful highly innovative products[J].
Industrial Marketing Management, 2004, 33(4): 307-316.
DOI: 10.1016/S0019-8501(03)00080-4. |
| [5] |
彭绍雄, 薄延珍. 基于云模型的装备研制项目中止决策方法[J].
船舶电子工程, 2012, 32(2): 93-95.
PENG Shaoxiong, BO Yanzhen. Termination decision methods of equipment development project based on cloud model[J]. Ship Electronic Engineering, 2012, 32(2): 93-95. |
| [6] |
金洪波, 侯强. 基于可拓理论的研发项目中止决策分析[J].
科技进步与对策, 2009, 26(7): 32-35.
JIN Hongbo, HOU Qiang. R & D termination decision methods based on extension theory[J]. Science & Technology Progress and Policy, 2009, 26(7): 32-35. |
| [7] |
汪洋, 孙林岩. 李克特式量表与模糊语言量表计分的差异比较—以梯形模糊数仿真为例[J].
运筹与管理, 2008, 17(1): 48-52.
WANG Yang, SUN Linyan. Comparing the score difference between the Likert scale and the fuzzy linguistic questionnaire: the simulating research of trapezoid fuzzy number[J]. Operations Research and Management Science, 2008, 17(1): 48-52. |
| [8] |
徐玖平, 吴巍.多属性决策的理论与方法[M].北京:清华大学出版社, 2006:226-232.
|
| [9] |
TSAI H H, LU I Y. The evaluation of service quality using generalized Choquet integral[J].
Information Science, 2006, 176(6): 640-663.
DOI: 10.1016/j.ins.2005.01.015. |
| [10] |
宋捷, 党耀国, 王正新, 等. 正负靶心灰靶决策模型[J].
系统工程理论与实践, 2010, 30(10): 1822-1827.
SONG Jie, DANG Yaoguo, WANG Zhengxin, et al. New decision model of grey target with both the positive clout and the negative clout[J]. Systems Engineering-Theory & Practice, 2010, 30(10): 1822-1827. DOI: 10.12011/1000-6788(2010)10-1822. |
| [11] |
管杜鹃, 郭鹏. 基于贝叶斯网络的项目组合风险度量[J].
工业工程, 2015, 18(4): 31-35.
GUAN Dujuan, GUO Peng. Assessment of project portfolio risk based on Bayesian Network[J]. Industrial Engineering Journal, 2015, 18(4): 31-35. |
| [12] |
王翯华, 朱建军, 方志耕. 基于案例分析的语言信息灰靶决策分类模型[J].
系统工程理论与实践, 2013, 33(12): 3172-3180.
WANG Haohua, ZHU Jianjun, FANG Zhigeng. Grey target cluster decision method on linguistic evaluation cased-based[J]. Systems Engineering-Theory & Practice, 2013, 33(12): 3172-3180. DOI: 10.12011/1000-6788(2013)12-3172. |
 2016, Vol. 19
2016, Vol. 19


