电力生产具有高度连续性,生产与消费同步意味着电力故障会对社会产生瞬时危害, 而电力物资是电力生产运行的保障。但是,电力企业物资管理普遍存在着匮乏和积压的双重现象:一方面,企业因物资储备不足而无法确保需求发生时的及时供应,产生高额缺货成本和社会经济损失;另一方面,企业因物资储备过量而导致积压与腐蚀,造成大量资金浪费。因此,电力物资的库存控制对电力企业至关重要。然而,大多数电力物资呈间断需求特性,即需求是随机的且需求数据中存在着大量零值,这些特点会给电力物资的库存管理带来很大的困难。
20世纪50年代以来,已有大量学术文献对库存控制方法进行了讨论,但是传统的库存控制方法大多针对连续需求,因而对间断需求是无效的[1-3]。考虑到复合分布可以分开表示需求到达过程和需求量,其结构和间断需求生成过程相似,所以许多学者[4-10]提出复合分布(尤其是复合泊松分布)可以为间断需求的库存物资分布提供良好的拟合。
在间断需求的背景下, 如果时间被视为离散变量, 那么需求到达服从伯努利分布或者二项分布,此时,若需求量服从任意非负分布,则该需求过程服从复合伯努利分布或者复合二项分布;如果时间被视为连续变量, 那么需求到达服从泊松分布,此时,若需求量服从任意非负分布,则该需求过程服从复合泊松分布。相较于伯努利分布和二项分布,泊松分布能捕捉到更多与需求发生相关的信息;并且由于复合泊松分布理论上可以得到标准的统计分布,相对简单,其在学术文献中是主流;此外,从对需求刻画的角度来看,复合泊松过程不仅可以描述间断需求还可以描述连续需求[11-12]。Matheus等[13]在需求服从复合泊松分布的前提下对(R, Q)库存策略中的再订货点R提出了精确和近似的两种计算方法,研究结果表明在大多数情况下用近似算法已经能够得到较好的再订货点R。马保国等[14]假定航材可修件的需求服从复合泊松分布,建立了(S-1, S)库存策略下的库存决策模型。李冰[15]对具有复合泊松需求的联合补充问题提出一启发式算法,在一定服务水平下,利用该算法可以寻找出使单位时间内平均成本最小的补充策略。虽然在许多运用复合分布的库存策略研究中,复合泊松分布占主导地位,但是复合泊松需求过程下的库存机制还有一些待解决的问题:1)许多研究都是以服务水平为导向而不是以成本为导向的[16];2)分析成本导向系统时没有考虑到提前期随机的情况[16];3)缺少适用于间断需求的库存控制的简便算法[17]。
针对上述问题,本文基于Babai[18]的研究给出了服从复合泊松分布的电力物资的(T, Q)最优固定订货量算法;然后通过对电力物资进行实证分析将此算法与传统的报童模型相比较。
1 模型介绍 1.1 模型背景和假设电力企业物资管理的目的是以合理的储备实现用最少的资金保证设备维修的需要。因此,以成本为导向的库存控制模型与电力企业库存管理的根本目标相一致。由于大部分电力物资呈间断需求特性,而复合泊松分布能够较好地拟合间断需求。考虑到伽马分布只定义非负值,具有可加性且涵盖了更为广泛的实际分布形状,能更好地拟合非零需求量。因此,将电力物资拟合成需求量服从伽马分布、需求到达服从泊松分布的复合泊松伽马过程。在此基础之上,采用(T,Q)库存策略,建立复合泊松伽马分布下的库存成本模型。
研究基于如下假设。
1) 单级单产品的库存系统;
2) 提前期随机,服从均值为L的一个一般分布;
3) 库存成本由持有成本与缺货惩罚两部分组成。
1.2 符号说明λ为平均需求到达率,β为平均需求量均值,X为需求量(随机变量),μx为平均需求量,σx为需求量的标准差,Y为提前期(随机变量),L为提前期均值,T为盘点周期,Q为固定订货量,h为单位库存持有成本,b为单位缺货惩罚,Xi为独立同分布随机变量X之和,Fi(i≥1)随机变量Xi的累计概率分布,(X)+=max(X, 0)。
1.3 模型建立建立服从复合泊松分布的(T, Q)策略下的库存成本最小化模型,求解使成本最小的物资最优订货量。其中,库存周期T定义为
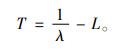
|
(1) |
对于服从复合泊松分布的物资,L个时间单位内需求到达i(i≥1)次的概率为
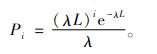
|
(2) |
设初始库存为Q,当i=0时,提前期内没有需求到达的概率为PD=e-λL,则所持有的库存未被消耗,此时库存持有成本为hQP0;当i≠0时,提前期内有i个需求到达,即需求量为Xi的概率如式(1)所示。此时,库存成本分2种情况:若订货量可以满足需求,即Q-Xi≥0,则库存成本按持有成本h计算;若订货量无法满足需求造成缺货,即Q-Xi < 0,则库存成本按缺货惩罚b计算。
系统中预期持有量与缺货量分别为Qp0+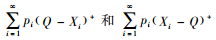
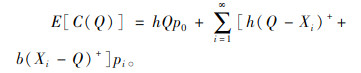
|
(3) |
即
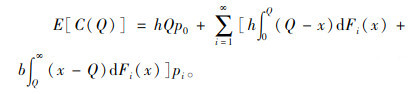
|
(4) |
本文的目标是找到可以最小化预期总成本的固定订货量。在库存成本函数中,订货量Q可以作为整体控制策略的变量,通过调节它来平衡缺货成本和库存成本,以最小化该订货量的库存物资将产生的库存成本。
由于当i≥1时,Q增加则Fi(Q)也增加,则导数也随着Q增加。因此E[C(Q)]是关于Q的凸函数,则可以通过导数为零得出最优的最大库存水平Q*。
命题1 最优最大库存水平Q*是式(5)的解
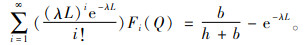
|
(5) |
证明:对式(4)求导得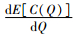
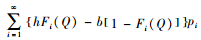
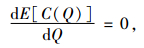
|
即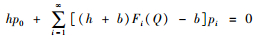
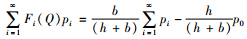
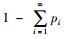
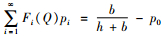
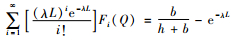
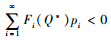
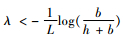
提出了一个可以用于计算最优最大库存水平Q*的闭式算法。由于式(5)中包含一个无限的和,因此,其数值需要截断来计算求解,所以本文需要通过上限QU和下限QL估计最优订货量。为了得到QU和QL,本文令
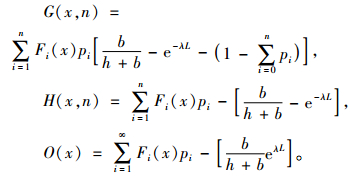
|
性质1 H(x, n)≤O(x)≤G(x, n)(对于所有的x,n≥0)。
证明: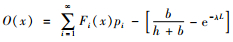
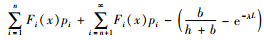
由于对于任意的x, i≥0,0≤Fi(x)≤1,则对于任意的x, n≥0,有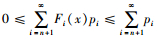
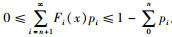
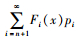
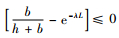
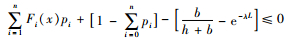
性质2 G(x, n),H(x, n)和O(x)都是x的增函数。
证明:G(x, n)、H(x, n)和O(x, n)都是由x组成的累积概率函数的和。由于这些累积概率函数是x的严格增函数,则G(x, n)、H(x, n)和O(x, n)也都是x的增函数。
性质3 当n趋向于无穷时,G(x, n)和H(x, n)逼近于O(x)。
证明:当n→∞,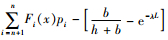
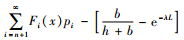
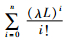
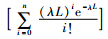
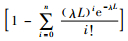
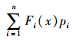
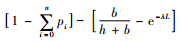
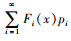
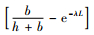
命题2 QL(n)≤Q*≤QU(n)是最优Q*的范围,其中, QU(n)和QL(n)分别是式(6)和(7)的解,
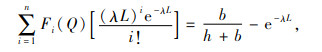
|
(6) |
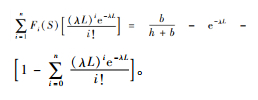
|
(7) |
并且当n趋于无穷大时,QU(n)和QL(n)的值逼近Q*。
命题2表明,对于不同的n值,QU(n)和QL(n)界定了Q*的一个范围,而当n增加时,这两个边界相互逼近,可以得到无限近似的Q*。
计算Q*的具体算法步骤如下。
步骤1:初始化任意小的ε(ε>0),n=1。
步骤2:计算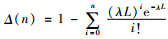
步骤3:如果Δ(n) < ε,转到步骤4;否则,n=n+1,转到步骤2。
步骤4:将n代入式(6)得到Q*。
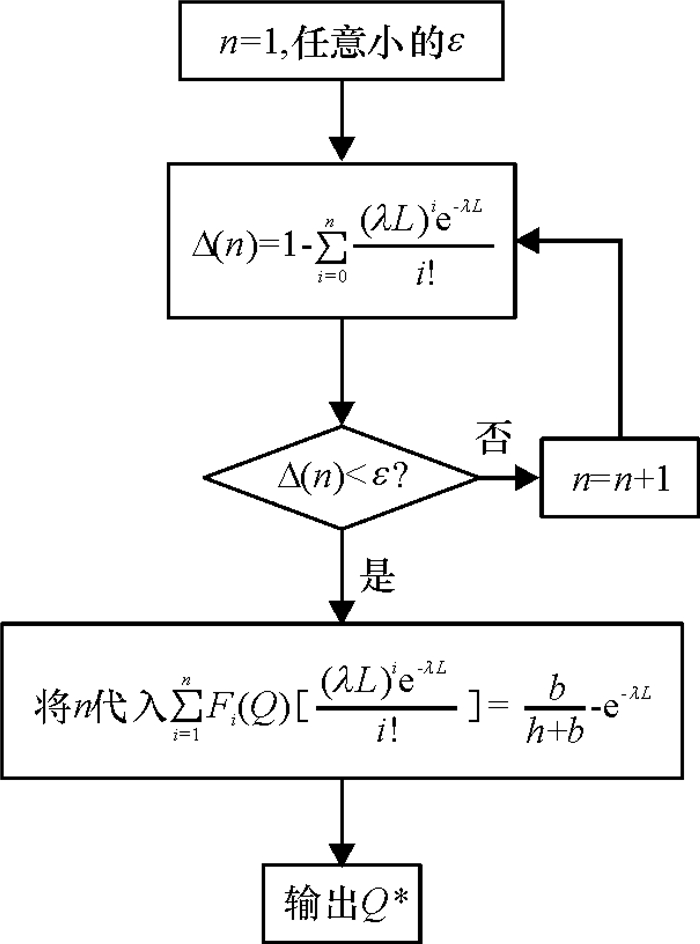
流程如图 1。
|
图 1 求解最优订货量Q*的算法步骤 Fig. 1 Algorithm steps of solving the optimal order quantity Q* |
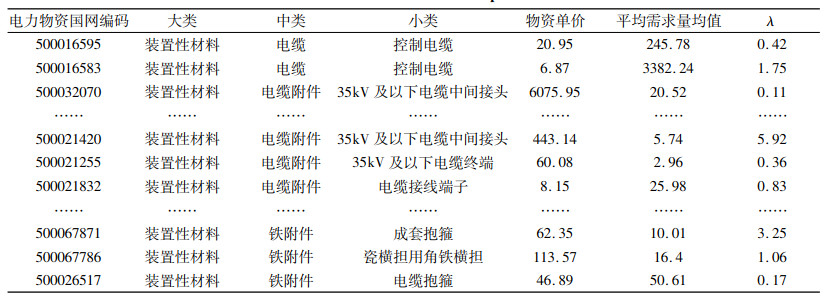
对上海电力公司757种电力物资在2011年至2013年共36个月的需求数据进行分布拟合,其中,服从复合泊松伽马分布的电力物资有576种。由于篇幅所限,本文以装置性材料大类下的50种服从复合泊松伽马分布的电力物资为例做实证研究。
电力物资总体信息见表 1。
| 表 1 电力物资数据总体信息 Tab. 1 Overall information of electric power materials |
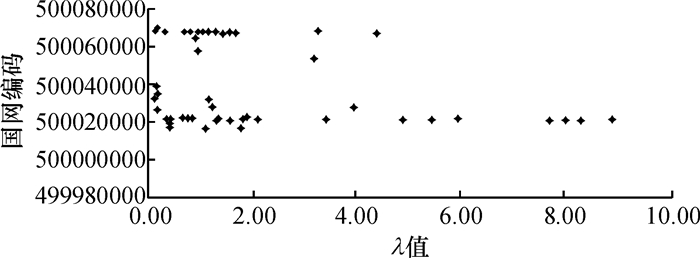
由表 1可知,这50种电力物资的平均需求到达率在0.11到8.86之间,如图 2所示。
|
图 2 50种装置性材料的λ分布图 Fig. 2 λ distribution figure of 50 kinds of installation materials |
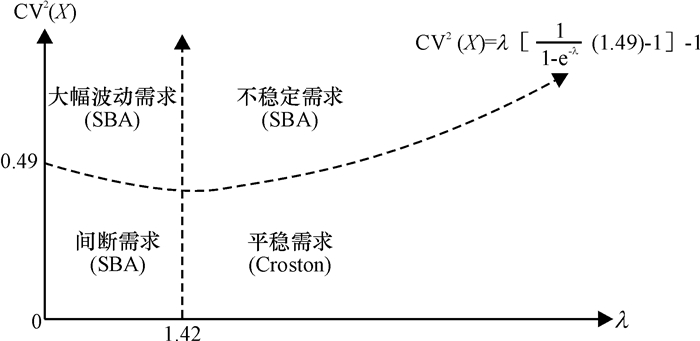
根据Lengu等[19]对服从复合泊松分布的需求分类标准(如图 3所示),当λ∈(0, 1.42]时,需求是间断的;当λ∈(1.42, +∞)时,需求是连续的。即这50种电力物资的需求虽然有少数是连续的,但大多数是间断的。用本文提出的方法对这50种电力物资的库存成本建模,求出各物资的最优订货量及其相应的平均库存成本,并将其与传统报童模型得出的结果相比较,探究在不同间断性水平下本文模型的有效性。
|
图 3 服从复合泊松分布的需求分类 Fig. 3 Classification of demand followsCompound Poisson Distribution |
由于电力企业的缺货惩罚远高于库存持有成本,不失一般性,本文设h=1,b=10。
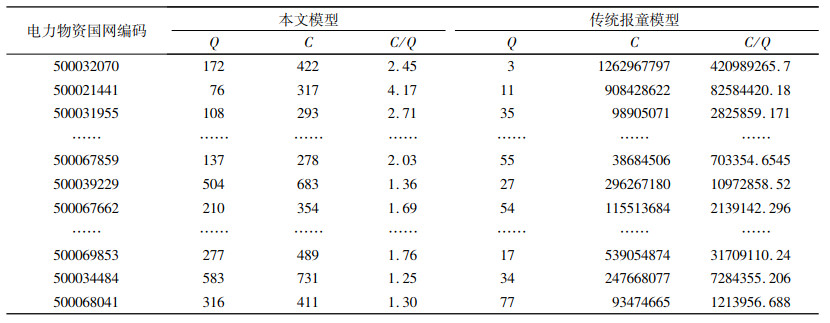
分别根据本文模型和传统的报童模型计算50种装置性材料的最优订货量及相应的库存成本、平均库存成本(C/Q),结果见表 2。
| 表 2 50种装置性材料的最优订货量 Tab. 2 Optimal order quantity of 50 kinds of installation materials |
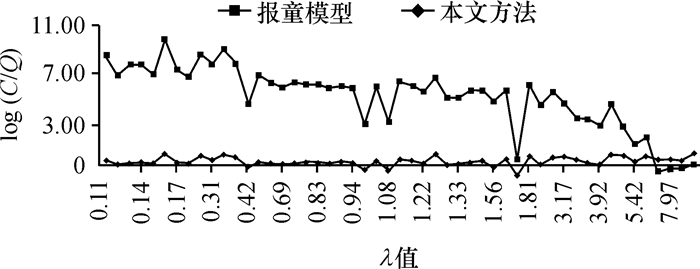
由于两种方法的计算结果的量级差异较大,为了便于比较,本文分别对两者取对数值,结果如图 4所示。
|
图 4 两种模型的平均单位成本比较 Fig. 4 Comparison of average unit cost between Newsboy model and our method |
如图 4,比较选取的50组电力物资的平均单位库存成本可知,当λ值较小(λ≤6)时,本文模型优于传统报童模型;而当λ值较大(λ>6)时,则相反。此外,随着λ值增大,模型相较于报童模型的优势逐渐减小。因此在企业的库存管理中,可以选用模型对间断需求的物资进行库存控制。
4 结论采用(T, Q)库存控制策略,对服从复合泊松分布的电力物资建立提前期随机和成本最小化的最优订货量模型,并将其与传统报童模型作比较。实证分析结果表明,当物资的需求偏间断时本文的最优订货量模型要优于传统报童模型,而随着物资间断性的减弱,本文提出的模型的优势也逐渐减小。
由于在此提出的最优订货量算法是通过数值模拟的方法得到,所以该算法不局限于电力物资,对于其他企业的间断需求的物资也适用。
| [1] |
DUNSMUIR W T M, SNYDER R N. Control of inventories with intermittent demand[J].
European Journal of Operational Research, 1989, 40(1): 16-21.
DOI: 10.1016/0377-2217(89)90267-1. |
| [2] |
STRIJBOSCH L W G, MOORS J J A. Modified normal demand distributions in (R, S) inventory control[J].
European Journal of Operational Research, 2006, 172(1): 201-212.
DOI: 10.1016/j.ejor.2004.10.002. |
| [3] |
SEGERSTEDT A. Inventory control with variation in lead times, especially when demand is intermittent[J].
International Journal of Production Economics, 1994, 35(1): 365-372.
|
| [4] |
FEENEY G J, SHERBROOKE C C. The (S-1, S) inventory policy under compound Poisson demand[J].
Manage Science, 1966, 12(5): 391-411.
DOI: 10.1287/mnsc.12.5.391. |
| [5] |
ARCHIBALD B C, SILVER E A. (s, S) Policies under continuous review anddiscrete compound Poisson demand[J].
Management Science, 1978, 24(9): 899-909.
DOI: 10.1287/mnsc.24.9.899. |
| [6] |
KI Lingcheung. On the(S-1, S) inventory model under compound Poisson demands and i.i.d. unit resupply times[J].
Naval Research Logistics, 1996, 43(4): 563-572.
DOI: 10.1002/(ISSN)1520-6750. |
| [7] |
BOYLAN J E. The centralisation of inventory and the modelling of demand[D].UK:University of Warwick, 1997.
|
| [8] |
JANSSEN F, HEUTS R. On the (R, s, Q) inventory model when demand is modelled as a compound Bernoulli process[J].
European Journal of Operational Research, 1998, 104(3): 423-436.
DOI: 10.1016/S0377-2217(97)00009-X. |
| [9] |
EAVES A H C. Forecasting for the ordering and stock holding of consumable spareparts[D].UK:Lancaster University, 2002.
|
| [10] |
TEUNTER R H, SYNTETOS A A, BABAI M Z. Determining order-up-to levels under periodic review forcompoundbinomial (intermittent) demand[J].
European Journal of Operational Research, 2010, 203(3): 619-624.
DOI: 10.1016/j.ejor.2009.09.013. |
| [11] |
MOINZADEH K. Operating characteristics of the (S-1, S) inventory systemwith partial backorders and constant resupply times[J].
Management Science, 1989, 35(4): 472-477.
DOI: 10.1287/mnsc.35.4.472. |
| [12] |
SMEITINK E. A note on operating characteristics of the (S-1, S) inventorysystem with partial backorders and constant supply times[J].
Management Science, 1990, 36(11): 1413-1414.
DOI: 10.1287/mnsc.36.11.1413. |
| [13] |
MATHEUS P, GELDERS L. The (R, Q) inventory policy subject to a compound Poisson demand pattern[J].
International Journal of Production Economics, 2000, 68(3): 307-317.
DOI: 10.1016/S0925-5273(99)00110-3. |
| [14] |
马保国, 张继强, 刘长新. 航材可修件复合泊松需求下的库存决策[J].
中国管理科学, 2004, 12(z1): 177-180.
MA Baoguo, ZHANG Jiqiang, LIU Changxin. The stock decision of repairable air material under compound poisson demand[J]. Chinese Journal of Management Science, 2004, 12(z1): 177-180. DOI: 10.3321/j.issn:1003-207X.2004.z1.044. |
| [15] |
李冰, 叶怀珍. 复合泊松需求的联合补充问题[J].
系统工程, 2002, 20(3): 9-14.
LI Bing, YE Huaizhen. Joint replenishment of problem with compound Poissondistribution[J]. Systems Engineering, 2002, 20(3): 9-14. |
| [16] |
LARSEN C, THORSTENSON A. A comparison between the order and the volume fill rate for a base-stock inventory control system under a compound renewaldemand process[J].
Journal of the Operational Research Society, 2008, 59(6): 798-804.
DOI: 10.1057/palgrave.jors.2602407. |
| [17] |
SANI B, KINGSMAN B G. Selecting the best periodic inventory control anddemand forecasting methods for low demand items[J].
Journal of the Operational Research Society, 1997, 48(7): 700-713.
DOI: 10.1057/palgrave.jors.2600418. |
| [18] |
BABAI M Z, JEMAI Z, DALLERY Y. Analysis of order-up-to-level inventory systems with compound Poisson demand[J].
European Journal of Operational Research, 2011, 210(3): 552-558.
DOI: 10.1016/j.ejor.2010.10.004. |
| [19] |
LENGU D, SYTETOS A A, BABAI M Z. Spare parts management: Linking distributional assumptions to demandclassi cation[J].
European Journal of Operational Research, 2014, 235(3): 624-635.
DOI: 10.1016/j.ejor.2013.12.043. |
 2016, Vol. 19
2016, Vol. 19