资源受限项目调度问题(resource constrained project scheduling problem, RCPSP)研究在满足一定的时序约束和资源约束条件下，安排各项任务的开始和完成时间，以实现项目的特定目标^[1]。在任务工期确定的情况下，对RCPSP的研究已经取得了大量的成果^[2]。然而实际环境中，项目往往受一些不确定因素的影响，使得项目工期具有模糊性，从而引出了对模糊资源受限项目调度问题(fuzzy resource constrained project scheduling problem, FRCPSP)的研究^[3]。

在FRCPSP的调度过程中，考虑到任务的时序约束，需要对任务的模糊工期进行比较，因此，许多模糊数弱比较方法被应用于FRCPSP的求解中。文献[4]采用PERT技术，文献[5]采用重心距离法和积分值法将模糊工期转化为精确值。文献[6]提出用积分值法、符号距离法以及基于面积的排序方法进行模糊数之间的排序比较运算。文献[7]利用可能性测度和必然性测度衡量任务模糊工期，并通过比较二者的权重和来确定两个模糊工期的大小。文献[8]计算出不同置信水平下模糊工期的下限和上限值，将其分别代入精确模型来求解问题。文献[9]基于一种区间数距离的排序方法比较模糊工期。上述文献采取了不同的方法来比较项目模糊工期的大小，对FRCPSP的求解均做出了贡献。但是这些方法都未考虑到任务工期模糊的环境下，项目关键路径有可能发生改变，各活动的模糊调度时间以及项目的模糊最短工期也可能随之相应地发生改变的问题。

另一方面，在算法求解过程中，由于粒子群优化方法(particle swarm optimization, PSO)易于实施，能快速得到问题的解，是有效解决FRCPSP的一种群智能算法^[10]。但是传统PSO由于算法自身的局限性，容易出现粒子早熟现象，使算法陷入局部最优。针对传统PSO的诸多不足，文献[11]将混沌算法嵌入PSO中，通过对比粒子群和混沌算法返回的全局极值大小，不断更新算法的全局极值，避免算法陷入局部极小值。文献[12]引入向量相似度法建立粒子速度的更新模型。文献[13]将重叠对齐技术引入到粒子调度生成机制中，改进了搜索过程中解的质量。上述方法分别从避免算法陷入局部极值以及提高迭代过程中解的质量方面对PSO进行改进，有效改善了算法的全局搜索能力。但是这些方法的优化结果与理想结果之间仍存在一定的差距。

为了解决上述问题，本文采用文献[14]提出的一种改进的模糊取最大运算来比较模糊工期的大小。同时，为了进一步提高求解这一问题的PSO的全局搜索能力，本文针对文献[15]提出的基于混沌和差分进化的混合粒子群优化算法，通过对算法惯性权重进行动态调整改进，将其引入到FRCPSP的求解中。

1 模糊资源受限项目调度问题

本文以项目模糊工期最短为目标，研究工期模糊情况下的资源受限项目调度问题。这里采用三角模糊数表示项目模糊工期。FRCPSP模型可描述如下：项目共由N(N=1, 2, …, n)个活动组成，每个活动都有时序约束和资源约束。时序约束表示，由于技术上的要求，活动之间存在着紧前紧后逻辑关系。记任意活动j的模糊工期为，其开始时间为。令表示在时刻执行中的活动集合，P_j表示活动j的紧前活动集合。对任意活动i∈P_j，如果i没有完成，活动j就不能开始。资源约束表示，完成项目需要K种可更新资源，第k(k=1，2，…, K)种资源的总量为R_k，完成任意活动j需要第k种资源的数量为r_jk，在项目完成前的任意时刻，正在执行的活动所需的该种资源总数不能超过该资源的总量。

FRCPSP的数学模型如下所示^[16]：

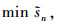
(1)

(2)

(3)

其中，式(1)为目标函数，表示项目的模糊工期取最小；式(2)为活动间的时序约束；式(3)为活动的资源约束。

2 模糊数排序

由于上述模型中式(1)目标函数表示的项目工期为模糊数，式(2)所示时序约束中要确定任意活动的模糊开始时间也要比较其所有紧前活动的模糊完成时间，这都需要比较两个模糊数之间的大小。针对这一问题，本文引入一种改进的基于区间数距离测度的模糊取最大运算^[14]来比较模糊数间的大小，解决了以往研究中忽略的工期模糊情况下，项目关键路径有可能发生改变，相应地FRCPSP最终调度结果中项目的模糊最短工期以及各活动的模糊调度时间也可能随之发生改变的问题。

假设有n个模糊数，不同α-cut值下，的隶属度值为。通过改进以往研究仅仅计算出两个模糊数的区间数距离^[17]，但仍无法确定两个模糊数相对大小的缺陷，文献[14]在文献[17]的基础上定义了用于比较的最大和最小理想点，如下。

(4)

(5)

在不同的α-cut水平下，任意模糊数与最小理想点的区间数距离如式(6)所示。

(6)

根据公式(6)，与最小理想点距离最大(小)的模糊数就是最大(小)的模糊数。同理，也可以利用最大理想点来比较模糊数之间的大小。

本文取最小理想点来比较模糊数之间的大小，因为取点相对更加客观，能避免文献^[14]在取不同理想点(最大理想点或最小理想点)时，造成的模糊数之间比较结果不一致问题(具体说明见算例分析部分)。此时，式(6)等价于如下形式：

(7)

3 混沌差分进化粒子群算法

本文将文献^[15]提出的基于混沌和差分进化的混合粒子群优化算法(chaos and differential evolution particle SWARM optimization algorithm, CDEHPSO)引入到FRCPSP的求解中，该算法利用混沌技术初始化种群，基于一种早熟判断机制识别出早熟粒子，并对其进行差分变异、交叉和选择以维持种群多样性。为了进一步提高算法的优化性能，本文对算法惯性权重进行动态调整改进，提出了混沌差分进化粒子群算法。

3.1 标准粒子群算法

PSO的数学描述如下：设种群规模为M，搜索空间维数为N，种群中第i个粒子迭代到第t代时其位置向量为X_i(t)={x_i1(t), x_i2(t), …, x_iN(t)}，速度向量为V_i(t)=v_i1(t), v_i2(t), …, v_iN(t)。粒子个体极值可以表示为lbest_i(t)，全局极值为gbest(t)，每个粒子分别按照公式(8)和(9)来更新其速度和位置^[18]：

(8)

(9)

其中，i=1, 2, …, M，j=1, 2, …, N。c₁和c₂为学习因子，r₁和r₂为分布在[0, 1]之间的随机数，t为迭代数，w为惯性权重。

3.2 混沌差分进化粒子群算法

1) 混沌初始化

设粒子群第j(j∈N)维空间变量的取值范围为[a_j, b_j]，在(0, 1)之间随机生成一个初始向量h₀=(h_{0, 1}, …, h_{0, j}, …, h_{0, N})，其中(h_{0, j}≠0.25, 0.5, 0.75)，向量h₀作为混沌Logistic映射的初始值，根据式(10)得到混沌序列h_{n+1, j}(μ为控制参数)：

(10)

再根据式(11)将混沌序列h_{n+1, j}映射到位置向量x_{n+1, j}，如下所示：

(11)

同理，可以得到粒子速度向量的初始化值。

2) 惯性权重更新策略

在迭代初期，算法惯性权重w取值应该较大，使算法进行全局搜索，迭代后期w取值应该较小，使算法快速收敛。针对这一问题，本文在文献[15]所提出算法的基础上引入一种非线性动态自适应惯性权重更新策略^[19]，其计算过程如下所示：

(12)

其中，t为当前迭代数，t_max为最大的迭代次数，w_max和w_min分别为惯性权重的最大和最小值，k为控制因子，控制w与t变化曲线的平滑度，通常取3。

3) 粒子早熟判断机制

文献[15]引入种群适应度方差来判断早熟粒子，适应度方差σ²的求解公式如下：

(13)

(14)

式中，f_i为第i个粒子的适应度值，f_avg为种群的平均适应度值，f为归一化因子，用于限制σ²的大小。通常，σ²越大，表示粒子越分散，种群多样性越好；σ²越小，表示粒子越集中，种群多样性越差。选取一个种群适应度方差阈值σ_T²，当σ² < σ_T²时，则判断出粒子进入早熟状态。

4) 对早熟粒子的差分进化操作

针对识别出的早熟粒子，对其进行差分进化算法中的变异、交叉以及选择运算，从而维持种群多样性^[15]，具体如公式(15)、(16)和(17)所示：

(15)

(16)

(17)

其中，x_{i, j}(t)代表第t代中第i条染色体的第j个基因，F为变异规模因子，Cr为交叉概率，z_{i, j}(t+1)代表变异向量，u_{i, j}(t+1)代表试验向量，rand_j是0到1之间均匀分布的一个数，rnb(i)是从1到N之间随机选择的数。

4 求解FRCPSP的混沌差分进化粒子群算法

本文采用基于活动优先值的粒子表示方式，同时，FRCPSP的调度生成机制有并行和串行两种方法，串行方法生成的是积极计划，并行方法生成的是非延迟计划，但其有可能会错过最优解^[12]，因此为了保证解的质量，本文采用串行调度生成机制，将由活动优先值表示的粒子转化为可行调度。

4.1 粒子表示方式

将每一个N维粒子与项目的N个活动相对应，用粒子位置向量X_i(t)={x_i1(t), x_i2(t), …, x_iN(t)}的N个参数值分别表示项目N个活动调度的优先值。

4.2 串行调度生成机制

1) 设CS是已排列的活动集合，DS是没有参加排列的活动集合。初始条件下，，DS={1, 2, …, N}。对各活动优先值进行降序排列，选择优先值最大的活动进行时序约束判断，若满足则进行下一步；不满足，则按优先值大小选择下一个活动判断，直到找出一个满足时序约束的活动为止；

2) 对所选活动进行资源约束判断，判断所选活动能否与已安排活动并行调度，可以则转下一步；不行，则将该活动安排到CS中，计算该活动的模糊开始时间，更新CS和DS，并返回第1)步；

3) 对上一步所选活动进行并行调度安排，根据式(7)比较各活动模糊工期大小，确定该活动的模糊开始时间，并将其安排到CS中，更新CS和DS，返回第1)步，直到安排完所有活动。

4.3 算法参数调整

在迭代过程中，为了避免不可行的粒子位置以及粒子由于速度过大运动到可行搜索空间的外部，对粒子的位置向量和速度向量进行调整，如下所示。

(18)

(19)

4.4 FRCPSP的求解步骤

步骤1  确定种群规模M、搜索空间维数N、惯性权重初始值w(0)、种群适应度方差阈值σ_T²等参数的取值。令t=0，初始化种群。根据串行调度生成机制，将由优先值代表的初始种群粒子转化为可行调度，从而计算其适应度。令每个粒子的适应度值为该粒子所代表FRCPSP解的模糊工期与[0, 0]点的区间数距离，依据式(7)比较各粒子适应度的大小，从而得到仍由优先值表示的初始种群的个体极值lbest_i(0)和全局极值gbest(0)；

步骤2  令t=t+1，根据式(12)计算当前迭代次数下的惯性权重w(t)值，再根据式(8)和(9)更新粒子的速度和位置，并根据式(18)和(19)对其进行调整；

步骤3  计算种群适应度方差σ²进行粒子早熟判断，若σ² < σ_T²则转到步骤4；否则转到步骤5；

步骤4  根据公式(15)、(16)和(17)，对早熟粒子进行差分变异、交叉和选择操作；

步骤5  将由优先值表示的粒子转化为可行调度，得出项目模糊工期大小。根据式(7)计算出各粒子适应度值，更新此代粒子lbest_i(t)和gbest(t)；

步骤6  检查算法是否满足终止条件，若满足则停止迭代，输出此时的最优解，否则，转到步骤2继续搜索最优解。算法整体流程如图 1所示。

5 算例分析

下面结合图 2所示的某项目网络图，分析验证本文所提出的方法。假设完成该项目所需某种可更新资源的总量为30，项目具体参数如表 1所示。采用本文所提出的算法求解该算例，首先对算法各参数进行赋值，令种群规模M=30，粒子维数N=7，μ=0.5，t_max=60，w_max=0.9，w_min=0.4，k=3，F=0.5，Cr=0.8，c₁=c₂=2，σ_T²=0.001，该算例最终调度结果如表 2、表 3和表 4所示。

根据表 2、表 3和表 4可以看出，工期模糊情况下，当α=0, 0.1, 0.2, 0.3, 0.4时，项目关键路径为1-4-6-7，各活动的模糊调度时间如表 2所示，此时项目最短工期为(175，223，272)；当α=0.5, 0.6, 0.7, 0.8时，项目关键路径由原来的1-4-6-7变成了1-3-6-7，FRCPSP的调度结果也相应地发生了改变，各活动的模糊调度时间由原来表 2的调度结果变成了表 3所示结果，项目最短工期也变为(179，213，282)；而当α=0.9, 1时，项目关键路径由1-3-6-7变为了1-2-5-7，此时FRCPSP的调度结果与表 3相同。而文献[5]求解出的项目模糊最短工期为一个固定的模糊数，并没有如上述结果所示考虑工期模糊情况下，项目模糊最短工期以及各活动的模糊调度时间可能会发生改变的问题。

另外，值得注意的是，根据文献[14]提出的模糊取最大运算，采取最小理想点时，不同α-cut水平下关键路径与本文所得结果相同；而采取最大理想点时，当α=0.8时，项目关键路径为1-2-5-7，使得文献[14]采取不同理想点时，计算结果出现不一致情况。考虑到活动持续时间总是大于零的，本文取最小理想点相对更加客观，能有效避免文献[14]取不同理想点时，造成的模糊数之间比较结果不一致问题。

为了验证所提出的混沌差分进化粒子群算法的寻优性能，利用上述算例求解过程中粒子的适应度值来评价比较所提出算法与文献[15]提出的CDEHPSO算法和标准PSO的优化水平。分别用这三种算法对上述算例进行20次测试，这里仅给出α=0.5时的比较结果，如表 5所示。从表 5可以看出，相比其它两种算法，所提出的混沌差分进化粒子群算法具有较优的搜索性能。

6 结论

本文研究了以项目模糊工期最小为目标的FRCPSP，采用一种改进的基于区间数距离测度的模糊取最大运算来比较模糊工期的大小。针对该问题提出的混沌差分进化粒子群算法，能有效维持种群多样性、避免粒子早熟，能快速求解出不同α-cut值下可能会发生改变的项目模糊最短工期以及各活动的模糊开始和模糊完成时间，解决了以往研究中忽略的工期模糊情况下，项目模糊最短工期及各活动的模糊调度时间可能会发生改变的问题。