2. 怀化学院 商学院,湖南 怀化 418000;
3. 华润电力控股有限公司,山西 太原 030051
2. Business School, Huaihua University, Huaihua 418000, China;
3. China Resources Power Holdings Company Limited, Taiyuan 030051, China
多巷道、多穿越巷道布置是立体仓库的一种重要布局形式,为了提高拣选效率,大多企业采用堆垛机代替人工拣选,堆垛机的运行路径成为制约拣选效率的主要瓶颈。Ratlif[1]针对单区双路径问题,提出用固定绕行策略解决,但没有提出合理算法。徐洪泽等人[2]针对多巷道问题的拣选方式、存储和路径策略进行了研究,应用遗传算法求解。靳萌等人[3]用动态规划结合改进的遗传算法解决多拣选路径问题,但算法消耗的时间却有很大的延长。王宏等人[4]利用遗传算法对双区型仓库中拣货路径优化问题进行了研究,算例中一车一单模式将拣货车容量限制假设成足够大。常发亮等人[5]考虑堆垛机所携带的货箱的容量限制,在堆垛机一次作业容量受限的情况下,提出一种遗传算法,针对垂直货架上的多个取货点,安排若干次拣选作业求得总的拣选路径代价最小。以上研究在算法上多以遗传算法作为切入点,在遗传算法基础上进行不同改进,提出了各种改进遗传算法或者混合算法。对于单堆垛机服务多巷道问题,同时又考虑周转箱限制因素,应用改进算法求解堆垛机最短运行路径,在企业仓库应用中有重要实用价值。
本文针对单堆垛机服务多巷道多穿越巷道立体仓库拣选路径问题,分析了含周转箱约束的求最短运行路径的数学模型,提出用遗传模拟退火混合算法求解。通过仿真与单独的遗传算法和模拟退火算法进行比较,论证了该混合算法在收敛速度和解的精确性方面的优势。
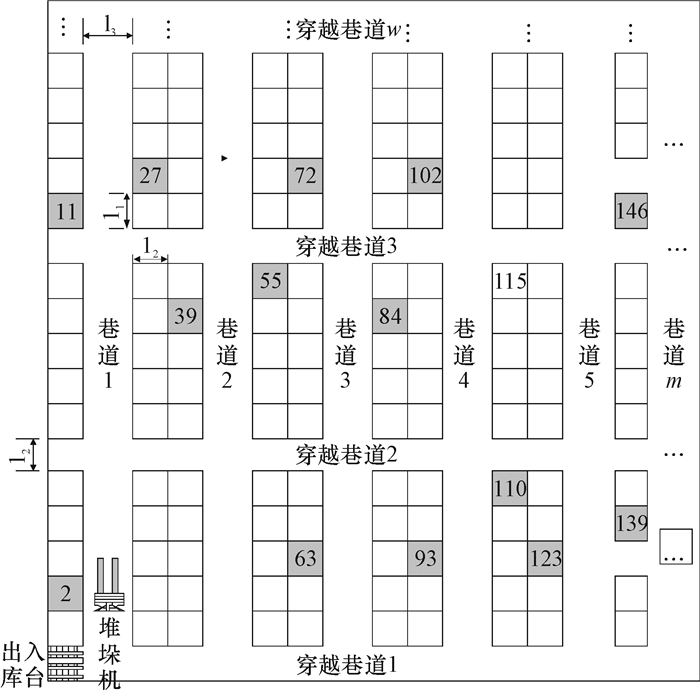
1 系统描述 1.1 问题的提出图 1是AS /RS一个存储区域的俯视图,一台堆垛机负责对存储区域的多排货架拣选, 相邻两排货架之间有一条巷道;每两排货架首尾相接处有一条穿越巷道,堆垛机在巷道和穿越巷道内运行存取货物;存储区左下角出入库台I/O(Input /Output);每个小方格代表—个货物储位,填充部分表示按某订单需拣取的货物所在的储位。根据客户货单,拣选作业过程为:计算机发出货单指令后, 堆垛机开始运动, 依照指令顺序,堆垛机依次拣选货物,待周转货箱满了,返回到I/O台更换空箱,直至完成该批订单,最后堆垛机携带货箱返回至I/O台,将货箱传送至输送系统,完成一次作业。
|
图 1 立体仓库平面图 Fig. 1 Stereoscopic warehouse planar graph |
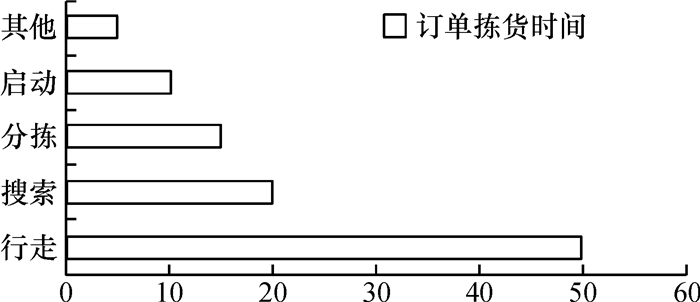
拣货的时间可分成行走(步行或车辆)时间、搜索时间、分拣时间等,如图 2所示。按照Tompkins的研究[6],行走时间常常占拣货时间的一半,因此本文研究重点是通过混合算法,找到堆垛机拣选的最短运行路径。
|
图 2 订单拣货时间的经典分配 Fig. 2 Classic allocation for order picking time |
m为巷道数,巷道编号以出入库点为参考,从左至右依次为1, 2, ..., m-1, m;
n为拣选任务数量;
w为穿越巷道数,穿越巷道编号以出入库点为参考,从下往上依次为1, 2, ..., w-1, w;
r为单排货位数量编号,即一层货格的列数,两个穿越巷道之间为一排,每排的货位数量编号为1~r;
qi为货位i处的货物体积;
Q为堆垛机容量;
l1表示货格的长度,l2表示货格的宽度,l3表示巷道宽度,l4表示穿越巷道宽度;
货位i到货位j的旅行距离为dij,拣选作业目标函数为[7]
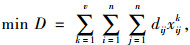
|
(1) |
约束条件:

|
(2) |
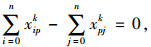
|
(3) |
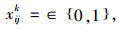
|
(4) |
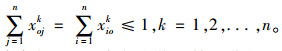
|
(5) |
约束条件(2)要求每次作业拣选货物的体积不能大于周转箱容积;约束条件(3)表示每次拣选作业经过的路线是连续的,即到达某个需求点时也必须从该点离开;约束条件(4)xijk=1表示第k次拣选作业先访问货位i再访问货位j,否则xijk=0;约束条件(5)表示每次拣选作业最多进行一次。
1.3 最短路径计算设出入库台在仓库的左下角,处于巷道1的左侧,穿越巷道1的左侧位置,求解堆垛机两点间最短运行路径,先判断两点位置关系:
1) 若货位i和货位j不在同一穿越巷道, 即wi≠wj,则
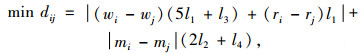
|
(6) |
2) 若货位i和货位j在同一个穿越巷道,但不在同一巷道,即wi=wj,mi≠mj,则
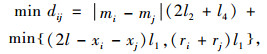
|
(7) |
其中,l代表单排货架的长度
3) 若货位i和货位j在同一个穿越巷道,且在同一巷道,即wi=wj,mi=mj,则
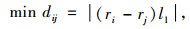
|
(8) |
4) 计算单次折返距离,需要记录每次的折返点,以[折回点,下一目标点]的形式表示,设为[e, f],则
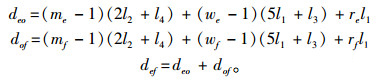
|
(9) |
遗传算法(GA)能从概率的意义上以随机的方式寻求到问题的最优解,其容易产生早熟现象,且局部寻优能力差[8-12]。模拟退火算法(SA)是模拟金属退火过程来寻找全局最优解的有效算法,具有摆脱局部最优点的能力[13-14]。用遗传算法与模拟退火算法相结合的方法,是解决上述问题的有效途径。
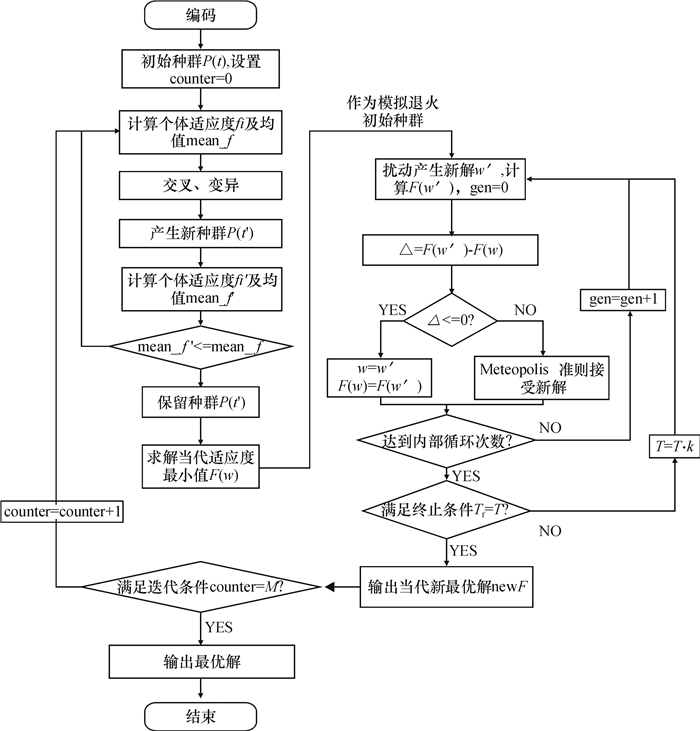
算法流程图如图 3所示。
|
图 3 遗传模拟算法流程图 Fig. 3 GSA flow diagram |
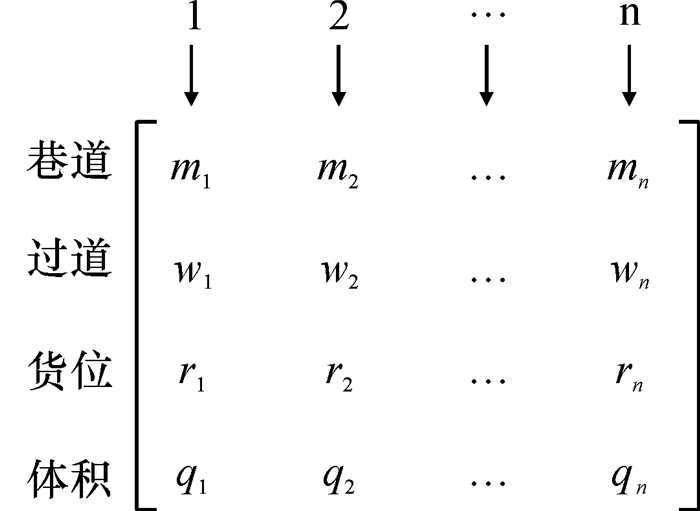
用(巷道码,穿越巷道码,货位码,体积码)组合来表示货位地址和对应货物体积。巷道码为货物所处的巷道编号,取值范围为1~m的自然数;本文将货架下方的穿越巷道编号作为该货架的穿越巷道码;货位码表示货架单层的货格数量,例如每层货架有5个货位,则货位码的取值为1~5的自然数;体积码表示货格中货物的体积;例如图 1中编号“39”的货位,其对应的编码为(2-2-4-q),代表该货位在第2个巷道,第2个穿越巷道上方,第4个货位,对应的体积为q。
本文采用自然数编码方式,假设n个拣选任务,1~n对应不同的货位点,其排列顺序代表不同的拣选路径方案,如染色体串{5, 4, 6, 2, 1},代表从出入库出发,依次拣选货位点5→4→6→2→1。编码规则如图 4所示。
|
图 4 编码与矩阵对应图 Fig. 4 Coded Reference to Figure |
N为群体规模,n为拣选任务货位总数,将1~n随机排列,产生一个N×n的矩阵,这个矩阵就是初始种群。每个染色体个体都是给定货单的一种可能的出入库顺序。设置当前进化代数counter=0,M为总进化代数。
2.3 计算适应度在本文中,将目标函数作为适应度函数f。根据模型公式,完成一次拣选的路径为:
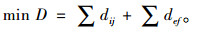
|
采用部分匹配交叉法可避免同一货位进行重复编码,部分匹配交叉操作要求随机选取两个交叉点,以便确定一个匹配段,根据两个父个体中两个交叉点之间的中间段给出的映射关系生成两个子代[9]。例如随机选择两个交叉点的父代为:
A=S-1-2-|3-4|-5-6,
B=S-4-2-|5-l |-6-3,
由中间映射关系3/5,1/4,最终得到子代为:
A'=S-4-2-5-1-3-6,
B'=S-l-2-3-4-6-5。
变异本身是一种局部随机搜索,与交叉算子结合在一起,保证了遗传算法的有效性,使遗传算法具有局部的随机搜索能力。在编码串中随机挑选一个或多个基因座,当变异概率pm大于随机概率,则以概率pm对这些基因座的基因值做变动。
一般情况下交叉概率pc取值为0.6~1,变异概率pm取值为0.001~0.1,这些参数对遗传算法的性能有重要的影响[9]。
2.5 选择通过判断适应度均值,选择均值小的一代种群遗传到下一代中,并取该代种群中适应度最小值对应的种群w作为模拟退火初始种群。
2.6 模拟退火算法Step1:初始化,设定当前最高温度TO,退火后温度Tf。
Step2:设定while(T>Tf)为外循环。
Step3:设定for gen=1:G为内循环。
Step4:把步骤3.5的解w作为模拟退火算法的初始种群,扰动产生新解w'。
Step5:评价子个体和相应父个体的适应度,若F(w')≤f(w),则无条件接受子代个体进入下一代,将更优的w'解赋给w解,即w=w';若F(w')>f(w),则按照Meteopolis准则,以概率P接受父代个体进入下一代。
Step6:判断gen=G?若不相等,将优化后的w返回到Step3;若达到内循环次数,输出w进入下一代。
Step8:调整控制温度T=T·k, 当T=Tf,则停止模拟退火算法,输出局部最优解newF;否则返回步骤Step2。
2.7 算法终止在进化后期,随着控制温度的降低,适应度值更小的个体被子个体所取代的概率也显著减小,可以保证本代中优秀的个体顺利的进入到下一代中。
每代计算后进行一次迭代次数叠加,counter=counter+1,当迭代次数达到最大迭代次数,即counter=M, 则算法停止,输出全局最优解,否则返回步骤3.3。
3 Matlab仿真评测 3.1 参数设定某仓库有5条巷道,3条穿越巷道,每条巷道分为左右两排,共10排货架(从左到右编号依次为1—10排),每层货架有5个货位,即r∈1~5,货格长宽l1=l2=1m,巷道宽l3=1.2m,穿越巷道宽l4=1.2m,周转箱容积Q=30dm3,任选15个货位点作为拣选任务,如图一所示。按仓库货位排序,选取的任务序号为:{2, 110, 146, 39, 84, 63, 123, 55, 93, 102, 11, 115, 72, 139, 27},对应货物体积为{5, 10, 8, 9, 7, 12, 7, 8, 9, 4, 6, 11, 4, 10, 6}。
3.2 仿真结果分析设变异概率pm=0.06, 交叉概率pc=0.5, 迭代次数M=100, 种群规模N=100, 初始温度To=95,最终温度Tf=0.001, 调整系数k=0.95,模拟退火内部循环次数为50,用MatlabR2011b进行仿真分析[15]。
1) 最优解分析
分别用遗传算法、模拟退火算法、遗传模拟混合算法20次进行仿真,结果如表 1所示。
| 表 1 三种算法仿真比较 Tab. 1 Comparison of simulation of three algorithms |
从上表 20次随机仿真结果可知,遗传算法计算结果中最大值、最小值分别与均值比较偏差范围为[-10.3,13.8],从各次仿真图形可看出遗传算法收敛过早;模拟退火算法随机性较大,计算结果偏差较大,稳定性差,求出的解不能代表最优解,仿真结果与均值比较偏差范围为[-19.6,15.4];而遗传模拟混合算法在遗传算法求得的优解基础上继续扩大搜索范围,防止遗传算法早熟现象,计算值比遗传算法和模拟退火算法更小,计算出的路径更短,仿真结果与均值比较偏差范围为[-2.8,5.2];从上表看出,混合算法各次仿真结果波动范围最小,最稳定,求出的解最接近最优解.
2) 收敛性验证
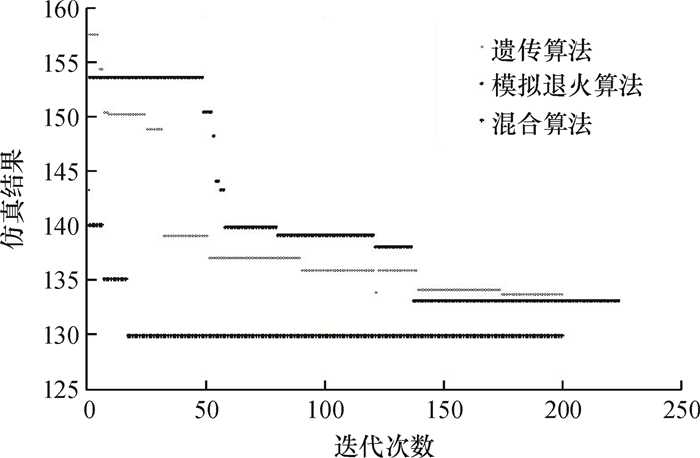
进一步上述比较3种优化算法的收敛性,设置随机50组仿真。为与模拟退火算法的迭代次数相近,将遗传算法和混合算法的最大迭代次数调整到200,用仿真结果相近的解,比较3种算法的收敛速度。对比可知,混合算法的收敛性较好,在迭代到15~30次之间就得到全局最优解,适应度值不再降低;遗传算法在迭代到150~200次之间,适应度值仍有下降趋势,并不是理想最优解;而模拟退火算法的收敛性跟初始种群的选择有关,有时在迭代100次左右收敛,有时在迭代150~200次之间收敛,结果不稳定。图 5表示的是其中一组适应度值相近的收敛性对比图。
|
图 5 收敛性比较 Fig. 5 Convergence comparison |
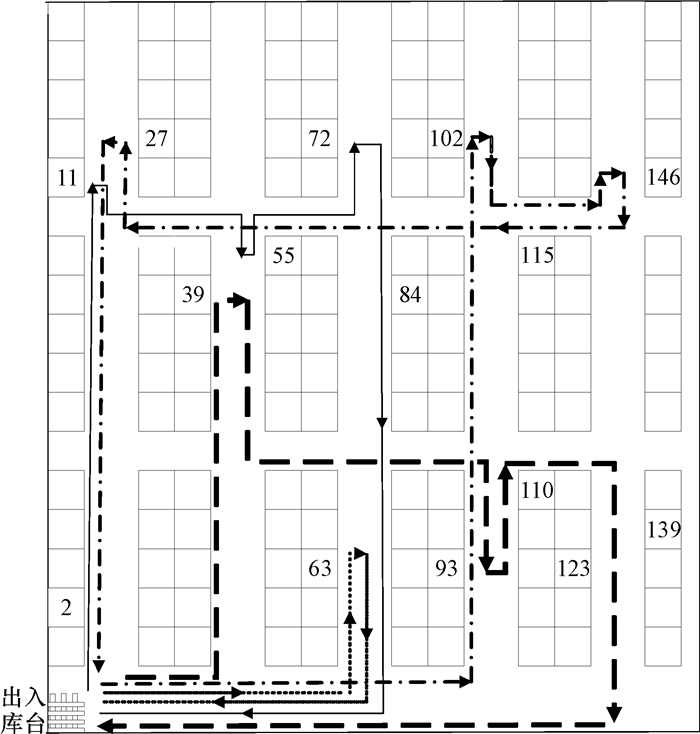
取50次仿真混合算法中适应度最小值125作为最优拣选路径,其对应拣选序列为:0→12→10→3→15→0→1→11→8→13→5→0→4→9→2→14→7→0→6→0,“0”代表出入库台。将这个拣选序列翻译到实际仓库模型中,按照仓库的货位编号,拣选分四次完成,路径分别为为:1)0→115→102→146→27→0,2)0→2→11→55→72→84→0,3)0→39→93→110→139→123→0,4)0→63→0。如图 6所示。
|
图 6 最优拣选路径 Fig. 6 The optimal picking path |
3) 稳定性可行性验证
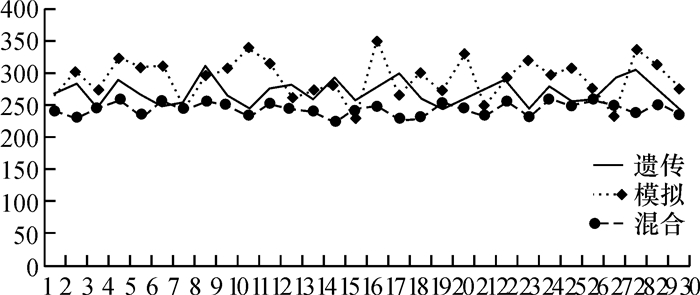
当扩大仓库容量,将拣选货单增加至30个,仿真30次,验证混合算法的稳定性及可行性。仿真结果如图 7所示:
|
图 7 三种算法稳定性比较 Fig. 7 Comparison of the stability of three algorithms |
从上图看出,当拣货订单增大,仓储空间增大,混合算法在求解堆垛机最短路径方面,比遗传算法和模拟退火算法有优势。求得的路径最短,每次仿真上下波动不大,稳定性更好,收敛速度更快。随着规模越大,遗传模拟混合算法表现出的优越性更明显,在实际应用中更有价值。
4 结论本文建立了含周转箱约束的多巷道堆垛机拣选作业模型,利用不同算法求解,通过Matlab对实例进行仿真验证。实验结果可以看出遗传模拟混合算法比单一的遗传和模拟退火算法的收敛速度更快,求出的解稳定性更好,精确性更高,计算结果上看,该混合算法更适合求解AS/RS中多巷道堆垛机拣选优化问题。但算法的计算量大约是单一的遗传算法的11 200倍,在今后的工作中应将重点放到优化算子的研究上,减少混合算法计算量。
| [1] |
RATLIFF H D, ROSENTHAL A S. Orderpicking in a rectangular warehouse:A solvable case of traveling salesman problem[J].
Operations Research, 1983, 31(03): 507-521.
DOI: 10.1287/opre.31.3.507. |
| [2] |
徐洪泽, 陈桂林, 张福恩. 遗传算法的单双点杂交方法对比研究[J].
哈尔滨工业大学学报, 1998, 30(2): 64-71.
XU Hongze CHEN Guilin ZHANG Fuen, CHEN Guilin, ZHANG Fuen. Comparison of one-point-crossover with two-point-crossoverin genetic algorithms[J]. Journal of Harebin Institute of Technology, 1998, 30(2): 64-71. |
| [3] |
靳萌, 穆希辉, 杜峰坡, 等. 基于动态规划与免疫遗传算法的多拣选路径规划研究[J].
计算机测量与制, 2013, 21(11): 3120-3123.
JI Meng, MU Xihui, DU Fengpo, et al. Dynamic programming and immune genetic algorithm—based multi—cross aisles order picking path planning studies[J]. Computer Measurement & Control, 2013, 21(11): 3120-3123. |
| [4] |
王宏, 符卓, 左武. 基于遗传算法的双区型仓库拣货路径优化研究[J].
计算机工程与应用, 2009, 45(6): 224-228.
WANG Hong, FU Zhuo, ZOU Wu. Genetic algorithm for picking routing problem in 2—block warehouse[J]. Computer Engineering and Applications, 2009, 45(6): 224-228. |
| [5] |
常发亮, 刘增晓, 辛征, 等. 自动化立体仓库拣选作业路径优化问题研究[J].
系统工程理论与实践, 2007, 27(2): 139-143.
CHANG Faliang, LIU Zengxiao, XIN Zheng, et al. Research on the order picking optimization problem of the automated warehuse[J]. Ystems Engineering-Theory & Pratice, 2007, 27(2): 139-143. |
| [6] |
TOMPKINS J A, WHITE J A, BOZER Y A, et a.Facilities planning[M]. New York:Wiley, 1996.
|
| [7] |
FILIPEC M, SKRLEC D, SLAVKO K. An efficient implementation of genetic algorithms for constrained vehicle routing problem[C]. Proceedings of IEEE International Conference on System, Man and Cybernetics, 1998.
|
| [8] |
吴柯. 一类高效的混合遗传算法[J].
计算机与数字工程, 2006, 34(10): 36-43.
WU Ke. An efficient hybrid genetic algorithm[J]. Computer & Digital Engineering, 2006, 34(10): 36-43. |
| [9] |
LEE S G, SOUZA R D, ONG E K. Simulation modelling of a narrow aisle automated storage and retrieval system (AS/RS) serviced by rail-guided vehicles[J].
Computers in Industry,, 1996, 30(3): 241-253.
DOI: 10.1016/0166-3615(96)00025-5. |
| [10] |
YAVUZ A B, WHITE J A. Travel time models for automated storage/retrieval systems[J].
Iie Transactions, 1982, 16(4): 329-338.
|
| [11] |
刘剑, 王鑫, 张冬梅, 等. 基于遗传算法的立体仓库堆垛机路径优化[J].
沈阳建筑大学学报(自然科学版), 2010, 26(5): 1006-1011.
LIU Jian, WANG Xin, ZHANG Dongmei, et al. Route optimization of stacker in automated storage and retrieval system based on genetic algorithms[J]. Journal of Shenyang Jianzhu University:Natural Science, 2010, 26(5): 1006-1011. |
| [12] |
周明, 孙树栋.遗传算法原理及应用[M].北京:国防工业出版社, 1999:83-84.
|
| [13] |
SELIM S Z, ALSULTAN K. A simulated annealing algorithm for the clustering problem[J].
Pattern Recognition, 1991, 24(10): 1003-1008.
DOI: 10.1016/0031-3203(91)90097-O. |
| [14] |
BAYKASOGLU A, GINDY N. A simulated annealing algorithm for dynamic layout problem[J].
Computers & Operations Research, 2001, 28(14): 1403-1426.
|
| [15] |
MATLA T, SUITE O, SHAMPINE L F, et.al.. The matlab ODE suite[J].
Siam Journal on Scientific Computing, 1997, 18(1): 1-22.
DOI: 10.1137/S1064827594276424. |
 2016, Vol. 19
2016, Vol. 19
