近年来，我国临床用血需求量迅速增长。尽管血液供应量也在持续增长，但仍然不能满足临床用血需求(如2010年与2009年相比，手术人次增长18.6%，而采血量增长仅7.7%)^[1]，血液供需矛盾日益尖锐，不少地方出现了严重的“血荒”现象。2010年~2014年，北京、重庆、深圳、上海、杭州、南京、成都等地出现不同程度的血库告急。2015年以来，血荒波及全国，多地出现10年来最严重的血荒，重庆市血液中心甚至启动了一级预警。血液短缺已呈现常态化、长期化趋势。此外，非常规突发公共卫生事件爆发后，受灾地的血液供给通常会锐减，出现严重的血液短缺乃至“血荒”现象。例如，2003年4月中旬随着SARS疫情的爆发，北京街头采血量从日均约350U(200ml/U)降至最低35U，导致临床用血高度紧张^[2]。因此，研究血液紧缺时的血液采集优化问题具有重要意义。

有关血液采集与库存控制问题的研究曾在20世纪70年代到80年代初达到鼎盛时期^[3-4]，此后有关该领域的研究迅速减少，但近年来又再次引起人们的关注。如高宝俊等^[5-6]建立了某大型医院血液最优订货点的离散事件仿真模型，并进一步考虑了血液制品需求受季节性波动影响的情形。吕昕^[7]基于历史数据使用Witness软件运行仿真模型，以求解最优采血点。Katsaliaki和Brailsford^[8]采用离散事件仿真模型研究了英国一家医院的血液库存管理问题。Simonetti等^[9]建立了美国血液保障中的库存仿真模型，以进行日常可用血液的评估，结果表明先进先出库存策略可以实现可靠的血液保障水平。Duan和Liao^[10]采用仿真优化模型研究了考虑血型替代情形下的医院红细胞库存问题，并用启发式算法进行求解。Haijema等^[11-12]分别采用马尔科夫动态规划与随机动态规划研究了血站内血小板的采集供应仿真模型。Van Dijk等^[13]采用随机动态规划与仿真技术研究了血小板生产中最优订购模式。此外，Kopach等^[14]应用排队模型研究了考虑常规需求和紧急需求下红细胞库存系统的最优策略。Zhou等^[15]研究了常规补货和紧急补货模式并存情形下医院的血小板库存管理策略。

可以看出，现有研究一般以医院或者血站为研究对象，且主要研究常态下的血液库存问题，而缺乏对血液紧缺情况下血液采集与库存控制问题的研究。有关应急条件下的血液采集文献尚不多见。刘波^[16]考虑血液寿命状态，建立了一个血液保障水平约束下的以报废率最小为目标的应急血液动态采集模型。在此基础上，周愉峰^[17]推导了两类具有不同新鲜度优先级的血液需求的库存状态转移方程，建立了一个应急血液采集决策动态模型及敏感性分析工具。但上述文献均以地震等大规模突发事件为应用背景，在应急血液供需关系上体现为需求爆炸性增长导致供血紧张。而本文以非典或者大规模血荒为应用背景，供需特点为血液供给大量缩减，而血液需求服从日常的随机分布。

此外，血液的一个重要特性是可以进行血型替代使用。在血液紧缺和应急情况下，这是保障血液供给的重要手段。此时血液采集决策就得考虑不同血型的替代问题。然而，目前考虑血型替代的血液采集问题研究极少，如Lang^[18]考虑血制品转运与替代策略, 研究多地点、多产品血液库存系统时的离散事件仿真模型。Duan和Liao^[10]考虑不同血型的替代性，以系统期望过期率最小为目标建立了红细胞的供应链库存仿真优化模型。这两者均采用仿真优化方法研究如何通过血制品的兼容替代来优化库存管理。本文则考虑了异型血替代策略对多类型血液制品库存控制的影响，以系统期望总成本最小为目标，建立了一个随机需求下的血液采集的离散混合整数规划模型，并针对模型性质，设计了一种精确算法。

1 模型构建 1.1 问题描述

不同血型血液制品的供应能力受到捐献者血型的影响。而献血者血型大致与该地区血型人口比例分布相同。当某地出现血液紧缺局面时，可能是某些血型供给较充足，而另一些血型供给较紧缺，紧急情况下不得不考虑不同血型血制品的替代使用问题。

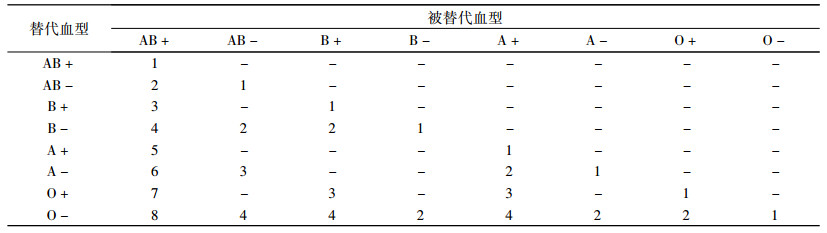
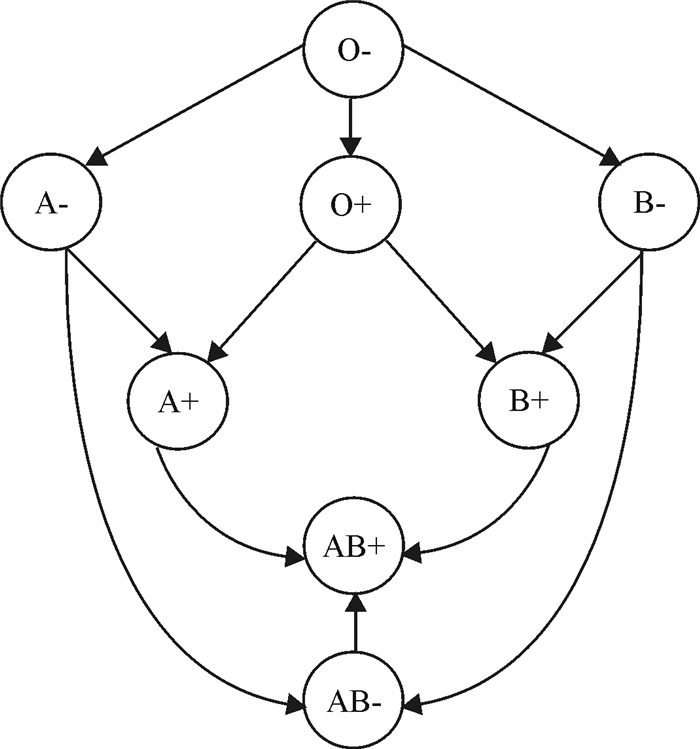
图 1给出了ABO血型系统各血型之间的替代关系^[21]。定义G={I, E}，其中，I为血型类型的集合，即I={i, k|A+, B+, AB+, O+, A-, B-, AB-, O-}；E为弧集合，表示节点两端的血型存在单向替代关系，E⊆I×I。例如，有向弧[i, k]i, k∈I表示血型i可替代血型k。设U_i为可被i型血替代的血型集合，即U_i={k|[i, k]∈E}，U_i⊂E。设V_i为可用来替代i型血的血型集合，则V_i={k|[k, i]∈E}，V_i⊂E。显然，某一血型可能可以替代多种其他血型(如图 1中, O-可以替代其他7种血型)，某一血型也可能可被多种血型替代(如AB-可被3种其他血型替代)。但因为“交叉匹配”风险的存在，血液的异型替代具有一定的优先级^[21]。如表 1所示，“1”表示替代优先级最高，“8”表示替代优先级最低，“-”表示不存在替代关系。在进行血型替代时，应优先采用高优先级的血型替代。

研究考虑血型替代的紧缺血液采集优化问题是要解决血液中心的采血决策和血型替代策略，即采集多少血液？血型之间如何替代以及替代多少？

1.2 紧缺血液采集成本分析

血液紧缺时虽然可以采用血型替代策略，但由于血型替代存在一定的风险，优化时应考虑血型替代的惩罚成本，且替代优先级越低，风险越大，惩罚成本越高。此外，医院缺血可能影响输血治疗患者的生命安全，须考虑缺血的惩罚成本，而血液中心的最优采集量短缺可能直接导致医院临床缺血。因此，紧缺血液采集在考虑采集成本，血液中心和医院的库存持有成本等日常运营成本外，还必须考虑血液中心的最优采集量短缺惩罚、以及血型替代产生的惩罚成本，医院的缺血惩罚成本等因素。

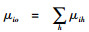
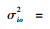
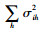
设o为血液中心；H为医院集合，h∈H。假设医院采取周期性检查的(R, S)(R为盘点周期，S为库存定至点)库存策略，血液中心采取连续性检查的(S, s)(S为库存定至点，s为血液采集点)库存策略。常规条件下各医院的临床血液日需求量服从相互独立的正态分布N(μ_ih, σ_ih²)^[5-7]，其中，μ_ih为h医院对i型血的日需求均值；σ_ih²为h医院对i型血的日需求方差，则血液中心的血液日需求量也服从正态分布N(μ_io, σ_io²)，且，。设L为血液中心的血液采集提前期，则提前期内的血液需求量也服从正态分布N(Lμ_io, Lσ_io²)。此外，设S_ih为h医院i型血的最大库存水平；SS_ih为h医院i型血的安全库存水平；ESL_h为h医院的实际库存服务水平；TSL_h为h医院的目标库存服务水平；Q_ih为h医院i型血的订购量；z_h为医院的库存服务水平因子；c_r为医院的单位血液库存持有成本；c_s为医院的单位缺血惩罚成本。Q_io为血液中心i型血的采集量；z_o为血液中心的库存服务水平系数；c_o为血液中心的单位血液库存持有成本；c_f为固定采血成本；c_v为可变采血成本；TP_io为血液中心采血的时间间隔。q_{i, short}为血液中心i型血的最优供给短缺量；c_short为血液最优供给量短缺的单位惩罚成本；y_ik为i型血替代k型血的数量；w_ki为k型血替代i型血的单位惩罚成本。

常规条件下，供应能力能够满足血液采集需求，血液中心存在最优的采集量Q_io^*(详见附录)和最大库存量S_io^*。然而，血液紧缺时S_io^*和Q_io^*不一定能实现，为保障血液供给，需采取血型替代、跨地区血液调剂、推迟手术等方法。设S_i为i型血的采集能力上限，当血液采集受限，即Q_io^*>S_i，∀i∈I时，需采集其他血型来替代血型i。该部分血量会产生一定的替代惩罚成本。若其他血型的可供替代量仍不足以将i型血可供给量补充至S_io^*，则将产生未满足最优采集量的惩罚成本。

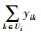
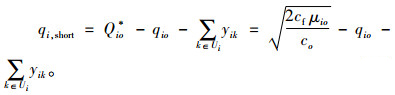
血型i的采集量根据用途可分为两部分：一是满足本血型需求的采集量q_io；二是用来替代其他血型的采集量。若i型血供给不足，则最优供给短缺量为

(1)

根据替代方向可将全部血型分为3类。

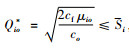
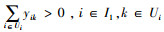
1) 输出型的富足血液。该类血型用I₁表示，除了供应本血型血液制品需求外，尚有采集能力替代其他血型。显然，I₁型血满足，且。

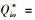
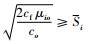
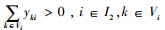
2) 输入型的短缺血液。用I₂表示该类血型，其自身采集能力不能完全满足需求，有部分紧急需求需以其他血型血液制品替代。I₂型血满足条件，且。

3) 平衡型的血液，可保障本血型的最优采集量，但不向外替代，用I₃表示。

1.2.1 I₁型血的库存成本分析

对于I₁型血，除了满足自身需求，还需整合用来替代其他血型需求的采集计划，则血液中心i(i∈I₁)型血总采集计划中，安全库存量、订货点、库存订至点分别为

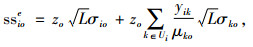
(2)

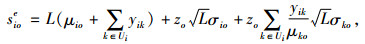
(3)

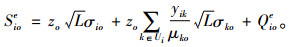
(4)

则血液中心i型血的日常周转库存成本为

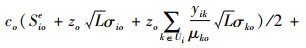
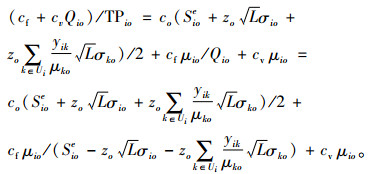
因此，血液中心I₁型血的日常周转库存总成本为

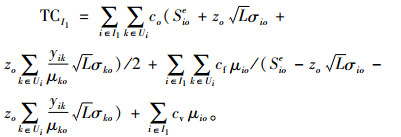
(5)

1.2.2 I₂型血的库存成本分析

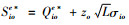
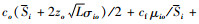
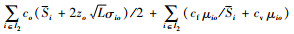
对于I₂型血，当采集血受限时血液中心i(i∈I₂)型血的最优采集量应为Q_io^e*=S_i，则最优库存订至点为。血液中心i型血的日常周转库存成本为c_vμ_io，则血液中心I₂型血的日常周转库存总成本为。

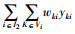
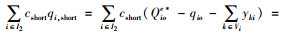
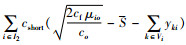
对于I₂型血，其部分需求采用其他血型血液制品替代、也有部分供应量未实现最优供给。因而除了日常运营成本，还需考虑异型学替代风险与最优供给量短缺的机会成本。

因此，血液中心I₂型血的库存总成本为

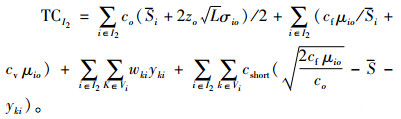
(6)

1.2.3 I₃型血的库存成本分析

对于I₃型血，其最优采集决策与常规条件下相同，故血液中心I₃型血的日常周转库存总成本为

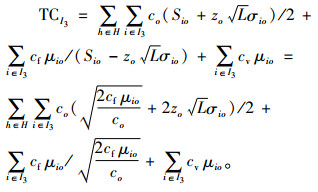
(7)

1.3 数学模型

至此，可建立考虑血型替代的紧缺血液采集优化模型如下。

MP：

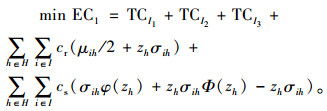
(8)

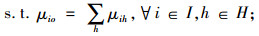
(9)

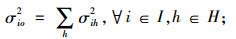
(10)

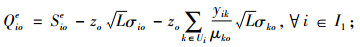
(11)

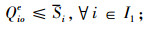
(12)

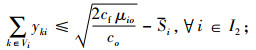
(13)

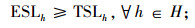
(14)

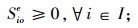
(15)

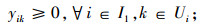
(16)

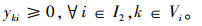
(17)

目标式(8)表示血液紧缺条件下血液中心和医院的期望库存总成本最小。约束式(9)和(10)表示血液供需平衡；式(11)为血液紧缺时I₁型血的采集量表达式；式(12)为I₁型血的采集量能力约束；式(13)为I₂型血的替代量约束；式(14)为医院的库存服务水平约束；式(15)~(17)为变量约束。

2 模型求解

由于目标式(8)的分母中含有决策变量S_io^e、y_ik和y_ki，因此MP为非线性规划模型，难以直接应用CPLEX等传统运筹学计算软件求解。为此，通过分析模型MP，发现可对其进行简化，将其分解为2个相互独立的子问题。

SP₁：

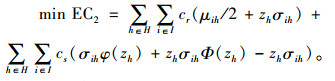
(18)

s.t.式(14)

SP₂：

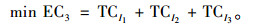
(19)

s.t.式(9)~(13)，式(15)~(17)

因为SP₁不含决策变量，SP₁与SP2完全独立，所以MP等价于SP₁+SP₂。又由于SP₁中的EC₂只与TSL_h相关，所以求解MP的关键在于SP₂。删除SP₂目标函数EC₃中的常数项，可将SP₂转化成RSP₂。

RSP₂：

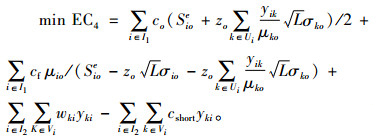
(20)

s.t.式(9)~(13)，式(15)~(17)。

SP₂转化为RSP₂只是剔除了目标函数中不涉及决策变量的成本项，而约束条件不变，故MP、SP₂、RSP₂具有相同的解集，即通过求解RSP₂得到决策变量S_io和y_ik的值，再将其代入MP即可求得系统期望总成本。

对EC₄进行转换可得

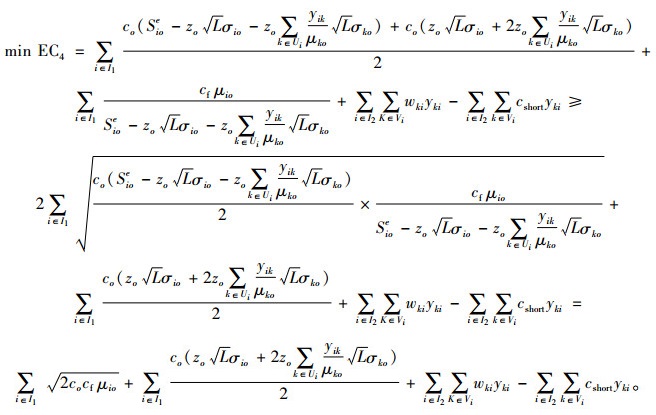
(21)

一般应有“医院缺血惩罚成本>>血液中心最优采集量短缺成本>>低优先级血型替代惩罚成本>高优先级血型替代惩罚成本>>血液采集和库存成本”。故由式(21)可知, 血型替代总量越大，期望成本越低；在血型替代总量一定的情况下，替代优先级越高，期望成本越低。

根据上述分析，设计如下精确算法

Step1  初始化，令。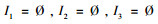

Step2  初步找出i∈I₁，i∈I₂。

若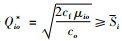，表明i型血紧缺，将i加入集合I₂；若Q_io^*<S_i，则将i加入集合I₁。遍历所有血型，直至I₁∪I₂=I。

Step3  找出集合I₂中不能被其他血型替代的紧缺血型。

对∀i∈{1, 2, ..., |I₂|}，若V_i∈I₂，表明可替代i的其他血型也紧缺。此时，采用Q_io^e*=S_i计算i型血的最优采集量，并将i从I₂中剔除。

Step4  找出集合I₁中不替代其他血型的富足血型，将其加入平衡型血集合I₃。

对∀i∈{1, 2, ..., |I₁|}，若U_i∈I₁，表明能被i替代的其他血型均富足，此时，将i从I₁中剔除并加入I₃。

Step5  对集合I₁和I₂中的任意血型，遍历所有替代情况。选择血液替代总量最大的替代方式，k型血替代i型血的数量计算公式为y_ki=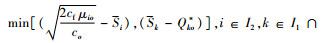_Vi；若血液替代总量最大的替代方式有多种，则选择高优先级的替代方式。若高优先级的血型替代方式也不是唯一的，则随机选择一种替代方式。替代方案确定后，若还存在i∈I₁，则将i加入集合I₃。

Step6  对任意i∈I₃，根据常规方案进行采血决策。

Step7  计算当前I₁集合中富足血液的采集量。

对于i∈I₁，求得y_ik后，再令式(A11)对S_io^e求导，可得无采集约束条件下考虑血型替代的最优库存订至点为

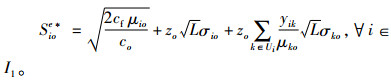
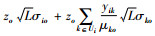
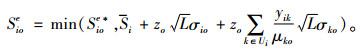
由式(11)和(12)可知，S_io^e的定义域为[0, S_i+]。因此，令实际的库存订至点为

又由于富足血液I₁满足条件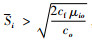，因此实际的库存订至点为S_io^e=S_io^e*, ∀i∈I₁。

Step8  将求得的决策变量值代入EC₁，可得系统的期望库存总成本。

上述算法遍历了所有血液替代组合，可以保证系统的期望库存总成本最小，从而获得问题的最优解。值得注意的是，最优解可能不止一个，因为Step5中可能存在多种最大替代量组合方式，或者存在多种同优先级的血型替代方式。

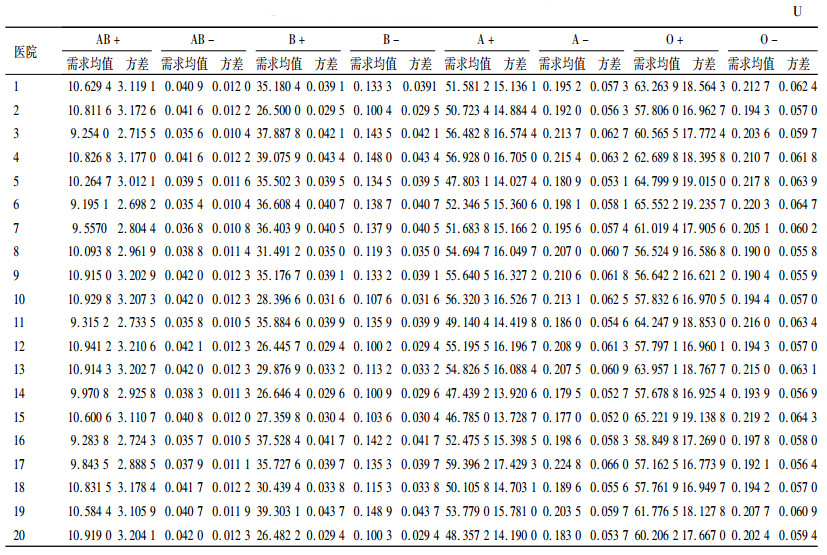
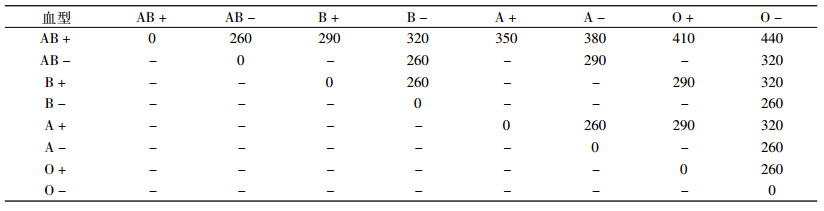
3 算例分析

以二级血液采供体系为例，系统内有1个血液中心负责血液采集，并对区域内的20家医院进行临床血液供应。20家医院的各血型血液需求量(单位:U)见表 2。其他参数设置如下：z_o=3.8，z_h=3.8(即目标库存服务水平TSL_h为99.99%)；L=1天；c_r=c_o=1元；c_v=1元；c_f=10元；c_s=1 000元；c_short=600元；8类血液的采集上限为[40, 1, 75, 8, 200, 4, 196, 3](单位:U)。异型血替代成本见表 3。

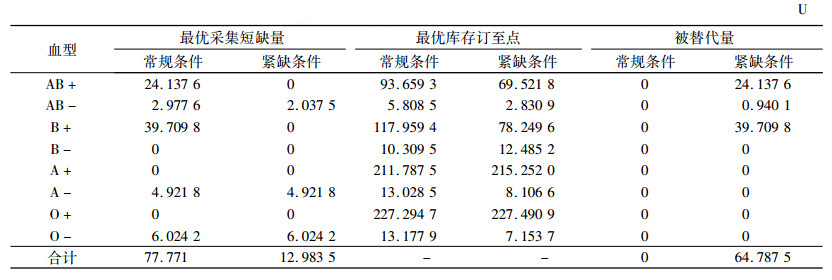
按照Step1~Step8求解模型，得到血型替代策略：B-替代AB-，替代数量为0.940 1U；O+替代B+，替代量为39.709 8U；A+替代AB+，替代量为24.137 6U。

同样，可以计算得到血液中心的库存方案。将该方案与常规状态进行对比。结果表明，最优血液采集短缺总量大幅下降(由77.771U下降到12.983 5U，见表 4)。将求解结果代入式(8)计算目标值，发现系统期望总成本由1 013 905.837元下降到256 780.779 9元，下降比例达74.67%，原因在于替代风险远小于血液采集短缺风险。因此，在严重性季节性血荒、区域性血荒，或者由SARS等造成血液供给严重不足的突发事件中，采用血型替代策略可有效缓解血液紧缺。

4 结束语

本文以部分血型血液产品紧缺为背景，分析了血型替代策略对血液制品库存控制的影响，并建立了一个系统预期总成本最小的血液采集优化模型。模型目标虽然为预期总成本最小，但重点考虑了血型替代成本、最优采集量短缺惩罚以及医院缺血惩罚成本等风险成本，可以较好地体现实际情况。根据模型特点，将问题分解为两个子问题，并提出一种精确算法。结果表明，本文提出的紧缺血液采集技术与替代策略，可降低血系统期望总成本74.67%，有助于缓解血荒，提高应急血液保障能力。

下一步可以研究考虑替代策略下的血液中心最优库存策略问题。此外，还可集成考虑外地血液调剂问题，分析血液调剂决策对紧缺血液采集决策和库存优化的影响。

附录

由于医院采取周期性检查的(R, S)库存策略，常规条件下各医院的临床血液日需求量服从正态分布N(μ_ih, σ_ih²)，则库存检查周期内各医院i(i∈I)型血的安全库存量、库存订至点、平均缺血量、库存服务水平分别为

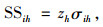
(A1)

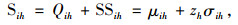
(A2)

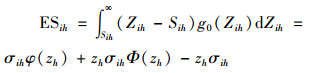
(A3)

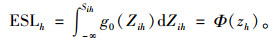
(A4)

式中，g₀(Z_ih)为h医院i型血的需求概率密度函数; Φ(·)和φ(·)分别为标准正态分布的分布函数和概率密度函数。

则h医院i型血的日常周转库存成本为

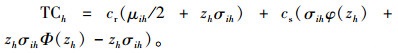
(A5)

血液中心采取连续性检查的(S, s)库存策略，日需求量服从正态分布N(μ_io, σ_io²)，则血液中心i型血的安全库存量、订货点、库存订至点分别为

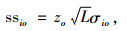
(A6)

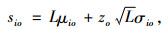
(A7)

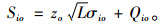
(A8)

则血液中心i型血的日常周转库存成本可表示为

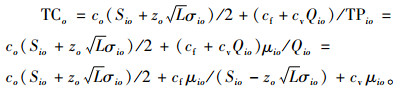
(A9)

因此，常规条件下血液中心和医院的库存总成本为

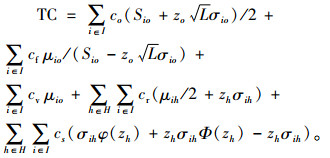
(A10)

令TC对S_io求导，可得常规条件下血液中心的最优库存订至点，即

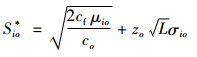
(A11)

将式(A11)代入式(A8)，可得血液中心i型血的最优采集量为

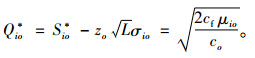
(A12)