随着世界人口的增长,食品消耗量也与日俱增,这给食品供应链管理带来巨大挑战,其中包括原材料供应商选择,分销渠道和运输模式选择,产品分配以及库存水平的确定等[1-2]。
传统供应链管理在处理供应链网络优化问题时主要考虑2个目标:缩减成本和提高订单响应速度。与传统供应链相比,食品供应链具有产品易腐性,食品质量等特殊性。另一方面,随着可持续发展逐渐深入人心,企业在制定主要物流目标时需同时将食品质量和环境保护纳入考虑范围。Steinfeldt等[3]的报告指出全球18%的温室气体排放是由畜产品产生的。因此,企业在做决策时需要将环境效益与经济、食品保鲜统一考虑。
目前,国内外已有许多关于食品供应链方面的文献。Bourlakis等[4]提出食品供应链中需要考虑的最重要的因素就是产品质量。Trienekens等[5]提出未来食品供应链在生产和配送过程中食品的质量保证将占据主导地位。Entrup[6]对酸奶酪供应链建立了一个混合整数规划模型,将保质期考虑在内。除了产品质量,食品供应链中另一个需要关注的重要特征就是易腐性。Goyal等[7], Raafat[8], Nahmias[9]提出了2种类型的腐败性:固定生命周期和随机生命周期。许民利等[10]对食品供应链建立了供应商和制造商食品质量投入的演化博弈模型,结果表明食品供应商与制造商的质量投入策略与双方质量投入产出比密切相关,当双方质量投入产出比不断变化时,出现多种演化稳定均衡。宋宝娥等[11]基于质量安全、价格成本、服务水平、管理水平和人员素质建立了超市生鲜食品供应商选择指标体系,运用熵组合权和TOPSIS法构建了供应商选择模型,并对模型进行了实证分析。刘凯飞等[12]针对5种关键风险因素,提出了生命周期固定的库存原材料的动态调度策略,结合运作风险及库存策略建立了多层级、多时段的易腐产品供应网络生产与配送过程的随机规划模型,最后结合实际案例分析了各种风险因子对供应链整体运作的影响。慕静等[13]从整个食品供应链的角度出发构建食品供应链安全等级评价指标体系,运用可拓评价方法建立可拓评价模型,并以乳制品供应链为例进行实证研究。陆欣等[14]针对食品供应链加工环节召回优化问题,给出4层批次分散模型,包含原料、部件、半成品、成品4个层次和分解、组合、包装3个加工流程,并提出了一种基于人工蜂群算法的召回优化方法,结果表明,该算法收敛较快,可以显著降低平均召回规模。
近年来,随着全球气温的上升以及环境的恶化,国内外专家学者在研究食品供应链时开始考虑温室气体排放的因素,其中最主要的是二氧化碳的排放,但是这方面的研究还处于起步阶段。Akkerman等[15], Seuring等[16]指出在食品供应链中除了食品的腐败性, 可持续发展也是一个新兴的研究领域,应给予足够的重视。Oglethorpe[17]提出食品供应链的复杂性要求从供应链的整体出发,结合经济,环境,社会效益作决策。Bosona等[18]通过建立族群和区域食品供应链网络一体化的方法,利用区位分析和路径分析设计区域食品供应链网络,有效地提高了市场潜力,物流效率,环境问题和对食品质量的跟踪。You等[19]为纤维素乙醇供应链建立了一个多目标规划模型,通过ε-约束法得到了一条帕累托最优曲线,揭示了可持续生物燃料供应链中经济,环境,社会维度之间的关系。
上述文献虽然从不同方面研究了食品供应链的特征,但都没有将食品供应链中食品质量,腐败性和环境问题进行综合考虑。基于此,本文在建立模型时考虑了食品的腐败率,并且在寻找碳排放源时综合考虑了食品的生产过程,配送中心的处理过程以及食品的运输过程所产生的二氧化碳。其中运输过程是碳排放的主要来源,本文提出运输过程中产生的碳排放量与车辆的运输速度有关,通过数学模型得出车辆的最佳运输速度。最后分析不同的碳单位价格和不同的食品腐败率对整个供应链效率的影响。
1 问题描述本文在供应链网络设计的基础上构建了一个混合整数非线性规划模型。该模型的目标是在满足客户需求的情况下使整个供应链网络的总成本最小,并且使碳排放量尽量少。如图 1所示,本文考虑三级供应链,农场到配送中心不考虑腐败率,配送中心到需求地考虑腐败率并用不同速度的车辆进行运输,不同的运输速度所产生的碳排放量不同。为了更好地研究该模型,本文进一步作以下假设。
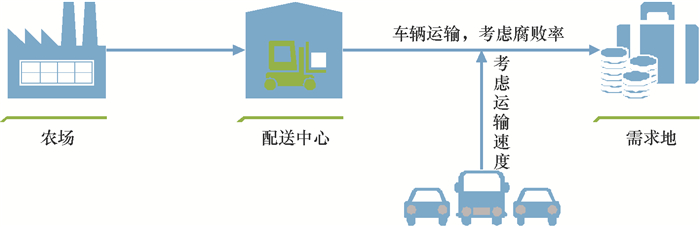
|
图 1 供应链结构图 Fig. 1 The structure of the supply chain |
1) 农场位置和个数,需求地位置和需求量都是确定的,配送中心的选址是未知的;
2) 产品从配送中心到需求地采用车辆运输,并且不同的车辆速度对应的碳排放量是不同的,同时考虑产品随时间的腐败率;
3) 假设车辆确定一个速度之后在其运输过程中速度保持不变;
4) 根据Bektas等[20]的研究,车辆速度与碳排放量间近似于呈二次函数关系。
2 模型建立为了方便该数学模型的描述,先对文中出现的符号和变量进行介绍,见表 1。
| 表 1 符号和变量 Tab. 1 Symble and variable |
0,1变量:

|
基于以上参数和变量,该模型构建如下,其中Dj、Pi、Qij、Tqjkm、Tjkm、Vjkm、TC为决策变量。
1) 目标函数。

|
(1) |
2) 约束条件。
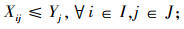
|
(2) |
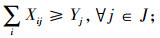
|
(3) |

|
(4) |
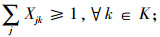
|
(5) |

|
(6) |

|
(7) |

|
(8) |

|
(9) |

|
(10) |

|
(11) |
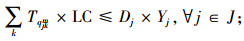
|
(12) |
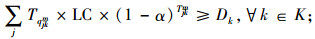
|
(13) |

|
(14) |

|
(15) |

|
(16) |

|
(17) |
在上述模型中,目标函数包括3个方面:式(1)表示整个供应链的运营成本。其中第一项是食品的生产成本,第2项为配送中心的固定成本,第3项是配送中心运营成本,第4项是车辆的租赁成本,第5项是农场到配送中心的运输成本,第6项为配送中心到需求地的运输成本。第7项表示整个供应链碳排放产生的社会成本,包括生产过程,配送中心处理过程以及运输过程中产生的碳排放引起的社会成本。第8项表示车辆司机的薪水。
在约束方面,式(2)表示只有当配送中心j运营时农场i才能与其产生运输关系。式(3)表示如果配送中心j运营,它可以接受多个农场的供货。式(4)表示只有当配送中心j运营时需求地k才能与其产生运输关系。式(5)表示需求地k能够接受多个配送中心供货。式(6)表示如果农场i与配送中心j之间有运量的话,那么它必须满足一个上限和一个下限。式(7)表示如果配送中心j与需求地k之间有运量的话,那么它必须满足一个上限和一个下限。式(8)表示农场i的实际产量等于从该农场运往配送中心的量。式(9)式表示农场i必须满足一个最低产量,但是又不能超过该农场的最大产量。式(10)式表示配送中心的实际容量等于运入该配送中心的量。式(11)式表示如果配送中心j运营,那么它的运营能力必须满足一个上限和一个下限。式(12)式表示从配送中心j运往需求地的量不能超过其存量。式(13)表示在考虑食品腐败率的情况下,运往需求地k的量必须超过其需求量。式(14)表示车辆从配送中心开往需求地所用的时间是一个整数,采取四舍五入的原则。式(15)表示车辆采用某个速度水平之后其所产生的每千米碳排放水平,其中a,b,c为常数。(16)和(17)式为非负约束。
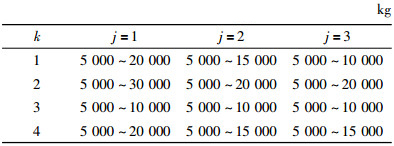
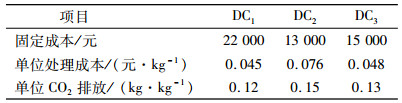
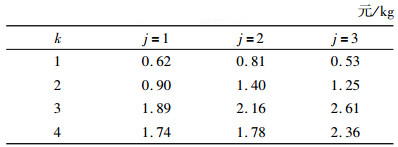
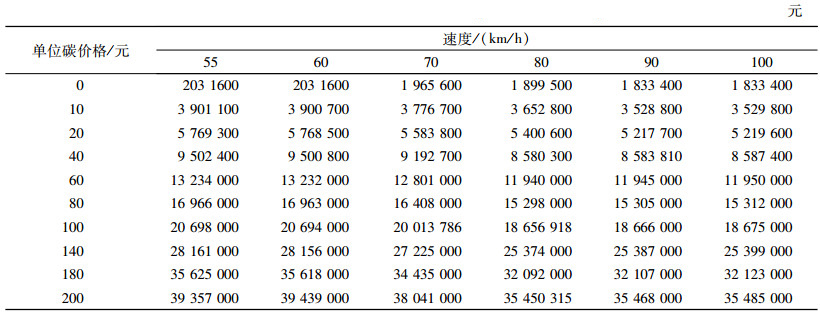
3 算例分析 3.1 数据与工具该模型应用于一个由5个农场,3个潜在配送中心和4个需求地构成的多级供应链网络。车辆在高速公路上的运输速度在60 km/h~100 m/h之间,因此本文选取了5个速度Vjkm=[60, 70, 80, 90, 100]进行研究;此外,为贴合实际,车辆还有可能走普通道路,本文假设车辆走普通道路时平均速度为Vjkm=55 km/h,并且此时所行使的距离为走高速时的1.2倍,分别研究车辆在这6个速度下供应链网络的结构以及整个供应链的总成本和总碳排放情况,并进行比较,得出车辆的最佳运输速度。各个农场的生产能力为:F1 =0~73 400,F2 =0~12 700,F3 =0~35 100,F4 =0~34 400,F5 =0~11 000;各配送中心的容量为:DC1 =50 000~80 000,DC2 =20 000~50 000,DC3 =20 000~55 000;各地需求为:D1 =25 000,D2 =50 000,D3 =20 000,D4 =30 000;租车成本rentcost=4 200元/辆,Cqijce=0.07,车辆载重LC =5 t/辆,α=0.1,SCRco2 =20元/t,W =25元/h,其他所涉及到的数据见表 2~表 10。
| 表 2 农场到配送中心之间各条线的运量限制 Tab. 2 The flow limitation of each line from farms to distribution centers |
| 表 3 配送中心到需求地之间各条线的运量限制 Tab. 3 The flow limitation of each line from distribution centers to demanding place |
| 表 4 与配送中心有关的数据 Tab. 4 The datum related to distribution centers |
| 表 5 与农场有关的数据 Tab. 5 The datum related to farms |
| 表 6 农场i到配送中心j的单位运输费用 Tab. 6 Unit transportation cost from farm I to distribution center j |
| 表 7 配送中心j到需求地k的单位运输费用 Tab. 7 Unit transportation cost from distribution center j to demanding place k |
| 表 8 农场i到配送中心j运输每单位产品的碳排放量 Tab. 8 Unit carbon emission for transporting one good from farm i to distribution center j |
| 表 9 配送中心j到需求地k的距离djk Tab. 9 The distance between distribution j to demanding place k |
| 表 10 车辆速度与每千米碳排放的关系 Tab. 10 The relationship between vehicle speed and carbon of unit kilometer |
本文使用MATLAB TOOL 2014a+YALMIP在2.20GHz CPU和2G内存的微机上对该模型进行求解。
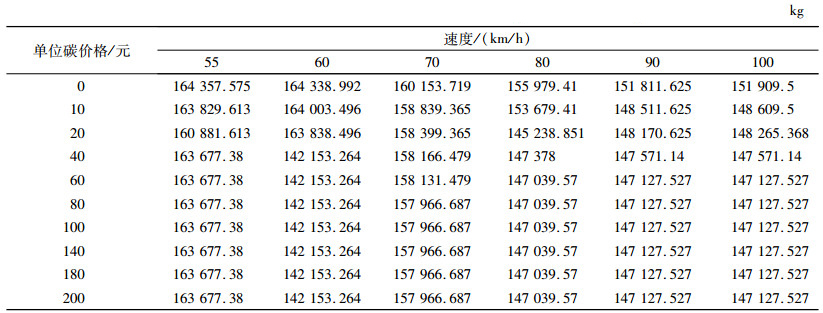
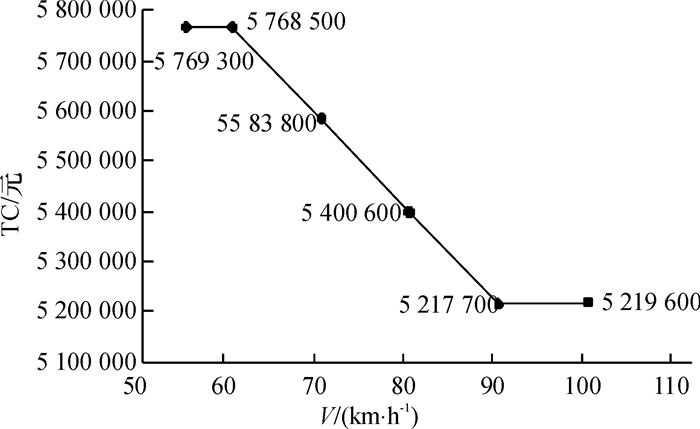
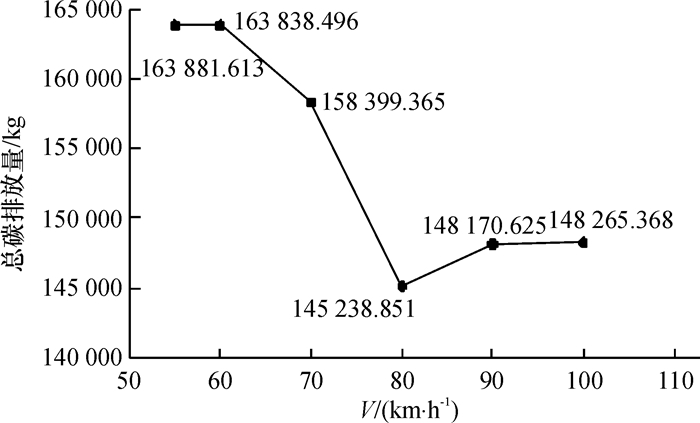
3.2 结果分析根据以上数据经过计算,得到以下结果,见图 2和图 3。当车辆的运输速度为90 km/h时,整个供应链的总成本最小,为5 217 700,此时总碳排放量为148 170.625;但当车辆速度为80 km/h时整个供应链的CO2总排放量是最少的,为145 238.851,此时总成本为5 400 600。如果企业注重经济效益,则可以将车辆速度设为90 km/h,如果注重环境效益,可以将车辆速度设为80 km/h。
|
图 2 车辆速度与总成本之间的关系 Fig. 2 The relationship between Vehicle speed and total cost |
|
图 3 车辆速度与CO2总排放量之间的关系 Fig. 3 The relationship between vehicle speed and total CO2 emission |
本文研究了不同碳单位价格,不同车辆速度下整个供应链的总碳排放量以及总成本的变化,结果见表 11,表 12。结果显示,当碳价格上涨时,供应链的总成本也随之上涨,说明政府可以通过提高单位碳价格调节整个供应链的经济效益以及环境效益;另一方面,在车辆速度一定的情况下,碳价格的上涨并不总能使碳排放总量下降。例如,在车辆速度为90 km/h,当碳价格从20到40以及从40到60时,CO2的总排放量是下降的,但当碳价格继续上涨时,CO2总排放量却没有继续下降,这是因为当碳单位价格持续上涨时,整个供应链的结构为了满足客户的需求不再发生变化。
| 表 11 不同碳价格,不同车辆速度下供应链的CO2总排放量 Tab. 11 Total carbon emission under different carbon price and vehicle speed |
| 表 12 不同碳价格,不同车辆速度下供应链的总成本 Tab. 12 Total cost under different carbon price and vehicle speed |
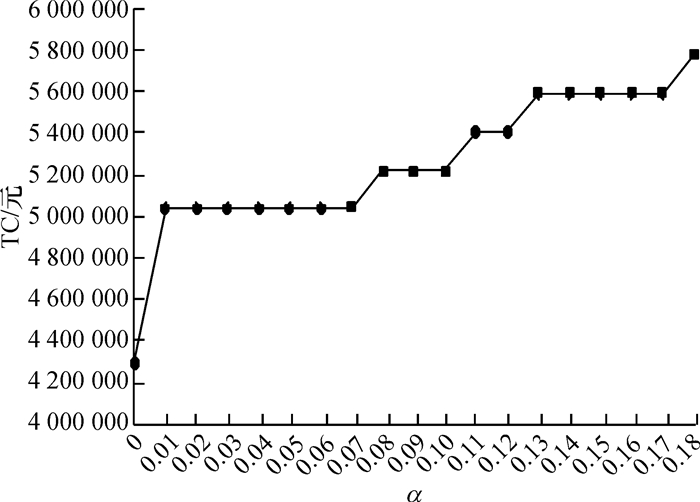
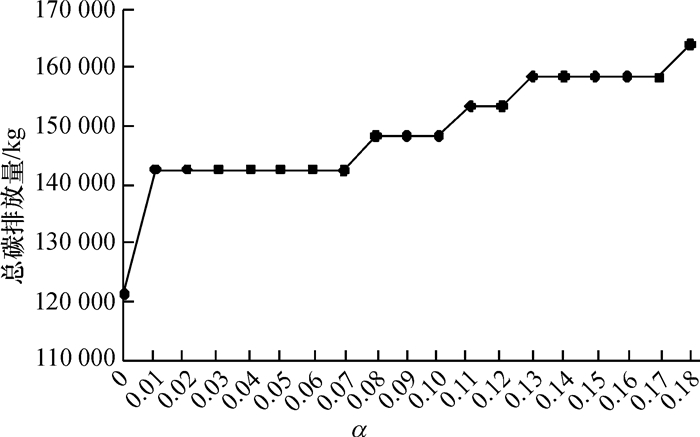
本文计算了车辆速度为90 km/h,碳单位价格为20元的情况下不同α值的变化对整个供应链网络的影响,得到表 13,图 4和图 5的结果。从中可以得出,随着α值的下降,供应链总成本和总CO2排放量的起伏情况,但总的趋势是下降的,且这两者的下降幅度是相对应的,当α值为0时,供应链的总成本和CO2总排放量骤降。因此,企业在运输蔬菜的过程中要尽可能的使腐败率趋于0,而这又需要企业加大技术和设备上的成本投入,如温度、湿度控制,通风状况,光照、氧气含量控制等,需要在未来进行深入研究。
| 表 13 不同α值下供应链的总成本和总CO2排放量 Tab. 13 Total cost and CO2 emission under different α value |
|
图 4 不同α值下供应链的总成本 Fig. 4 Total cost under Differ ent α value |
|
图 5 不同α值下的供应链的总CO2排放量 Fig. 5 Total CO2 emission under different α value |
为了缓解全球温室效应的影响,降低CO2排放成为了一件紧迫的事情。正是考虑到这个原因,本文强调在食品供应链管理中考虑CO2排放具有重大的意义。在此所提出的模型对于政府来说也有一定的参考作用。政府以及立法者可以通过控制车辆运输速度或者对碳价格进行设定,从而在环境效益和经济效益之间取得权衡。
虽然本文提出的模型对当前可持续供应链管理的研究具有一定的贡献,但是本文也有一些局限性需要更进一步的研究。1)在研究环境问题时,只考虑了最主要的温室气体CO2的排放,实际上,更多的温室气体应该被考虑在内,比如N2O,SO2等。2)在本文中,车辆从配送中心将蔬菜运到需求地之后没有考虑下一步的活动,所以,在未来的研究中,逆向物流以及循环物流应该被纳入考虑范围之中。3)在考虑环境问题时,本文考虑的因素还是不够多,其中如水资源、能源的利用在以后的研究中也应该被考虑。
| [1] |
HARRIS I, NAIM M, PALMER A. Assessing the impact of cost optimization based on infrastructure modeling on CO2 emission[J].
International Journal of Production Economics, 2011, 131(1): 313-321.
DOI: 10.1016/j.ijpe.2010.03.005. |
| [2] |
CORDEAU J F, PASIN F, SOLOMON M M. An integrated model for logistics network design[J].
Annals of Operations Research, 2006, 144(1): 59-82.
DOI: 10.1007/s10479-006-0001-3. |
| [3] |
STEINFELD H, GERBER P, WASSENAAR T, CASTEL V. Livestock's Long Shadow. Environmental issues and options[R]. Rome: FAO, 2006.
|
| [4] |
BOURLAKIS M A, WEIGHTMAN P W H. Food Supply Chain Management[M]. Oxford: Blackwell Publishing, 2004.
|
| [5] |
TRIENEKENS J, ZUURBIER P. Quality and safety standards in the food industry. Developments and challenges[J].
International Journal of Production Economics, 2008, 113(1): 107-122.
DOI: 10.1016/j.ijpe.2007.02.050. |
| [6] |
LÜTKE, ENTRUP M, GÜNTHER H O. Mixed integer linear programming approaches to shelf-life-integrated planning and scheduling in yoghurt production[J].
International Journal of Production Research, 2005, 43(23): 5071-5100.
DOI: 10.1080/00207540500161068. |
| [7] |
GOYAL S K, GIRI B C. Recent trends for modeling deteriorating inventory[J].
European Journal of Operational Research, 2001, 137(1): 1-16.
|
| [8] |
RAAFAT F. Survey of literature on continuously deteriorating inventory models[J].
Journal of the Operational Research Society, 1991, 42(1): 27-37.
DOI: 10.1057/jors.1991.4. |
| [9] |
NAHMIAS S. Perishable inventory theory: a review[J].
Operations Research, 1982, 30(4): 680-708.
DOI: 10.1287/opre.30.4.680. |
| [10] |
许民利, 王俏, 欧阳林寒. 食品供应链中质量投入的演化博弈分析[J].
中国管理科学, 2012, 20(15): 13-141.
XU Minli, WANG Qiao, OUYANG Linhan. The analysis of evolution game of quality investment in food supply chain[J]. Chinese Journal of Management Science, 2012, 20(15): 13-141. |
| [11] |
宋宝娥, 朱文茵, 李晓明. 基于TOPSIS法的超市生鲜食品供应商选择模型研究[J].
食品与机械, 2013(4): 223-228.
SONG Bao'e, ZHU Wenyin, LI Xiaoming. The sutdy of supplier selectron model in supermarket fresh food based on TOPSIS[J]. Food and Machinery, 2013(4): 223-228. |
| [12] |
刘凯飞, 刘晓. 考虑运作风险的易腐产品生产配送随机规划模型[J].
工业工程, 2013, 16(1): 38-44.
LIU Kaifei, LIU Xiao. The model of perishable food production and distribution stochastic programming considering operation risk[J]. Industry Engineering Journal, 2013, 16(1): 38-44. |
| [13] |
慕静, 贾文欣. 食品供应链安全等级可拓评价模型及应用[J].
科技管理研究, 2015, 35(11): 207-211.
MU Jing, JIA Wenxin. The expandable evaluation model and use of food supply chain safety rank[J]. Science and Technology Management Research, 2015, 35(11): 207-211. DOI: 10.3969/j.issn.1000-7695.2015.11.041. |
| [14] |
陆欣, 沈艳霞, 张君继. 基于人工蜂群算法的食品供应链召回优化[J].
江南大学学报(自然科学版), 2015(2): 166-171.
LU Xin, SHEN Yanxia, ZHANG Junji. The optimation of food supply chain recall based on artificial beecolony algorithm[J]. The Journal of Jiangnan University(Natural Scrence Edition), 2015(2): 166-171. |
| [15] |
AKKERMAN R, FARAHANI P, GRUNOW M. Quality, safety and sustainability in food distribution: a review of quantitative operations management approaches and challenge[J].
OR Spectrum, 2010, 32: 863-904.
DOI: 10.1007/s00291-010-0223-2. |
| [16] |
SEURING S, MULLER M. From a literature review to a conceptual framework for sustainable supply chain management[J].
Journal of Cleaner Production, 2008, 16(15): 1699-1710.
DOI: 10.1016/j.jclepro.2008.04.020. |
| [17] |
OGLETHORPE D. Optimizing economic, environmental, and social objectives: a goal-programming approach in the food sector[J].
Environment and Planning A, 2010, 42(5): 1239-1254.
DOI: 10.1068/a42292. |
| [18] |
BOSONA T G, GEBRESENBET G. Cluster building and logistics network integration of local food supply chain[J].
Biosystems Engineering, 2011, 108(4): 293-302.
DOI: 10.1016/j.biosystemseng.2011.01.001. |
| [19] |
YOU F, TAO L, GRAZIANO D J, SNYDER S W. Optimal design of sustainable cellulosic biofuel supply chain: Multiobjective optimization coupled with life cycle assessment and input-output analysis[J].
AlChE Journal, 2011, 58(4): 1-24.
|
| [20] |
TOLGA BEKTAS, GILBERT LAPORTE. The pollution-pouting problem[J].
Transportation Research Part B, 2011, 45(8): 1232-1250.
DOI: 10.1016/j.trb.2011.02.004. |
 2016, Vol. 19
2016, Vol. 19