2. 武汉理工大学 物流工程学院,湖北 武汉 430063
2. School of Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China
关键链项目管理(critical chain project management,CCPM)是Goldratt于1997年提出的项目管理领域的新理论。找出制约项目顺利完成的瓶颈-关键链,并在行为假设的前提下,运用缓冲技术来保护关键链,从而实现在动态环境中保护项目整体的思想,是关键链项目管理方法显著区别于现有项目管理技术,并受到持续推崇的根本原因。
CCPM关注和解决的基本问题是经典的、面向时间优化的资源受限项目计划与调度问题(resource constrained project scheduling problem,RCPSP)[1-2]。与之不同的是,CCPM较传统的RCPSP问题的求解又前进了一步,它并不停止于得到问题最优或者近优解,还需进一步识别制约项目进度的关键链,并以此为基础进行计划的调度。
Leach[3]、Tukel等[4]、莫巨华[5]、田文迪和崔南方[6]、Rabbani[7]、管在林等[8]、马国丰等[9]分别从不同角度构建了启发式的关键链识别算法,但都以RCPSP问题的求解为基础。众所周知,RCPSP问题属于NP Hard问题,主要有精确算法和启发式求解法。启发式计算方法又分为基于优先规则的启发式求解法和元启发式求解法(又称智能优化算法[10])。然而从可接受的计算时间和计算效率考虑,基于优先规则的启发式求解算法仍然是实际生产运作以及商业软件中使用最广泛的技术方法。但是不同启发式规则的使用会对同一项目调度问题产生不同的结果,进而影响到关键链的识别以及关键链项目管理方法的使用效果。因此探索先进的基于优先规则的关键链识别算法具有理论和实际双重意义。
本文拟构建一个两阶段关键链识别的启发式求解算法。第一阶段针对单项目、经典RCPSP问题的求解,介绍一种新的优先规则—活动的重心(the activity’s center of gravity,ACG),以最小活动重心为活动进行优先值赋权,采用并行调度法则[11],联合正、反向迭代技术[12-15],建立一种新的面向RCPSP问题的启发式求解方法;第二阶段进行关键链的识别,根据第一阶段迭代计算得到的不同结果,进一步利用活动的执行时间参数或者动态规划的方法进行关键链的识别。
1 活动的重心及重心定理 1.1 活动的重心(ACG)及亏值定理 1.1.1 活动的重心活动的重心一值是乞建勋在文献[16]中提出的,计算公式为
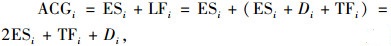
|
(1) |
ESi,LFi分别为CPM网络下活动i的最早开始时间和最迟完成时间;Di为活动i的工期;TFi为活动i的总时差。同时该论著探讨了CPM网络下n元序链的优化问题,提出了一般n元序链亏值定理。
1.1.2 n元序链亏值定理当n个平行工序A1,A2,…,An调整为顺序工序,即A1→A2→…→An时,称后者为n元序链;由工序顺序化所产生的项目工期延迟称为n元序链的亏值,记为[A1A2…An]。
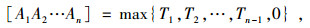
|
(2) |
Tk为n元序链第k阶(1≤k≤n)特征值:
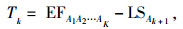
|
(3) |
LS为CPM网络下活动的最晚开始时间。
1.1.3 重心定理利用n元序链亏值定理,可以证明重心定理:当2个平行工序顺序化时,将重心较小的工序排列在前,获得的次序最优,带来的项目工期延迟最小,当项目网络中其它条件不变时。
当3个平行工序顺序化时,情形开始变得复杂,需要一些附加条件才能够判断最优次序。对于此问题,乞建勋证明了首工序定理和末工序定理。
[首工序定理]若ESA≤ESB,ESC, 且LFA≤LFB, LFC,则A一定在最优链的首位。即最优链是(A→B→C)或者(A→C→B)。
[末工序定理]若ESA,ESB≤ESC, 且LFA,LFB≤LFC,则C一定在最优链的末位。即最优链是(A→B→C)或者(B→A→C)。
虽然首(末)工序定理与重心定理之间不是充分必要关系,但是满足首(末)工序定理且位于最优链首(末)位的工序重心最小(大)。总结重心定理和首、末工序定理给予的启示,建立以活动重心为优先规则的,以并行调度为基础的,运用正反向迭代技术的两阶段启发式算法来进行关键链的识别(an iterative method for critical chain identifying using activity’s center of gravity as priority rule)。简单起见,称之为迭代重心法(I-ACG)。
2 基于活动重心定理的关键链识别法-迭代重心法迭代重心法识别关键链包括2个计算阶段,第一阶段求解RCPSP问题,第二阶段在第一阶段计算结果的基础上进行关键链的识别。
2.1 第一阶段——迭代重心法求解RCPSP问题第一阶段计算流程如下:
1) 利用关键路径法(CPM)求解问题,得到各活动的初始时间参数ES和LF,利用式(1)计算各活动的重心ACG。
2) 正向-1(Forward1)计算。
采用并行调度法,由p阶段组成,每有工序完成则推进到下一阶段;在新的时间节点tp处构建3个活动集合Cp,Ap和Sp,分别代表到时间节点tp止,已完成活动、正在进行活动和可调度活动集合;位于Sp中的活动,其紧前活动已完成,且资源需要量满足当前资源约束条件。
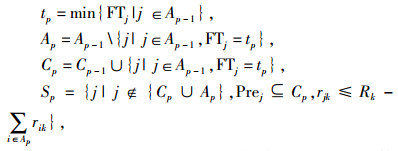
|
Sp中拥有较小重心的活动优先安排;重心相等时,优先选择工期较长的活动;工期相等时,优先选择网络编号小的活动。
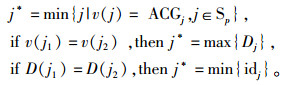
|
反复迭代,直到所有的活动都被安排,则当前计算结束,得到各活动满足执行和资源双重约束的正向-1计划和正向-1工期(ForwardSchedule1和ForwardDuedate1)。
FTj为活动j的完成时间;K为资源种类;Rk为第k种资源最大可供数量; rik为活动i所需第k种资源的数量。
3) 反向-1(Backward1)计算。
反向计算仍然从零时刻开始进行;不同的是Sp中的活动,其紧后活动都已完成,且资源需要量满足当前资源约束条件。
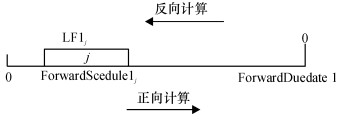
通过以下关系联系正向-1和反向-1计算, 见式(4)和图 1。
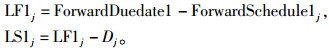
|
(4) |
|
图 1 正向-1计算与反向-1计算关系 Fig. 1 The relationship between forward-1 calculation and backward-1 calculation |
Sp中拥有较小最迟开始时间的活动优先安排;最迟开始时间相等时,优先选择编号较小的活动。
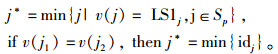
|
反复迭代,直到所有的活动都被安排,则当前计算结束,得到各活动满足约束的反向-1计划和反向-1工期(BackwardSchedule1和BackwardDuedate1)。
4) 判断。
a) 如果BackwardDuedate1>ForwardDuedate1,则计算终止,正向-1计算中得到的调度计划为项目可行计划,正向-1工期为项目完工期;
b) 如果BackwardDuedate1≤ ForwardDuedate1,则继续进行正向-2计算。
5) 正向-2(Forward2)计算。
通过以下关系联系反向-1和正向-2计算:
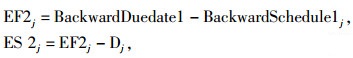
|
(5) |
Sp中拥有较小最早开始时间的活动优先安排;最早开始时间相等时,优先选择编号较小的活动。
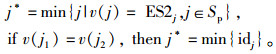
|
反复迭代,直到所有的活动都被安排,则当前计算结束,得到各活动满足约束的正向-2计划和正向-2工期(ForwardSchedule2和ForwardDuedate2)。
6) 判断。
a) 如果ForwardDuedate2>BackwardDuedate1,则计算终止,反向-1中得到的调度计划为项目可行计划,反向-1工期为项目完工期;
b) 如果ForwardDuedate2≤BackwardDuedate1,则回到第3步,进行反向-2计算,计算方法同反向-1计算。
如此反复进行迭代计算,直到项目工期不再改善,则计算终止。迭代重心法第一阶段计算流程如图 2所示。
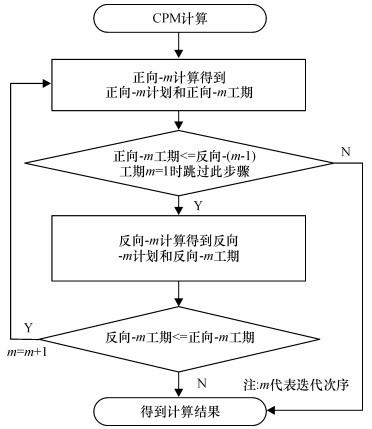
|
图 2 迭代重心法(I-ACG)第一阶段计算流程 Fig. 2 process of I-ACG first calculation stage |
1) 在第一阶段迭代计算过程中,如果在两个迭代方向同时得到最优(近优)工期,即:在某次序迭代得到
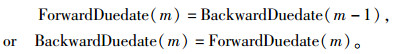
|
(6) |
则正向计算对应的计划为项目最早资源可行时间计划,反向计算对应的计划为项目最晚资源可行时间计划。正向计划与反向计划中活动的最早开始时间等于最晚开始时间的活动构成关键链。
2) 如果仅在一个迭代方向得到最优工期,则按文献[6]介绍的,用动态规划的思想,对得到的最优(较优)调度计划逐步右移、或者左移的启发式算法来识别关键链和非关键链。
流程如下图 3所示。
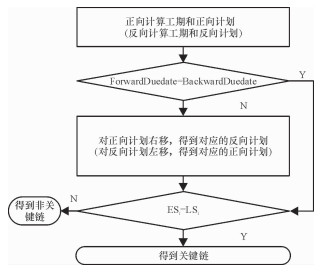
|
图 3 迭代重心法(I-ACG)第二阶段流程 Fig. 3 process of I-ACG second calculation stage |
本文选用Patterson110问题集作为问题样本,同时选用Kolisch和Özdamar[17-21]等总结出的3种表现较好的启发式规则:最小时差(minSlack),最迟完成时间(minLFT),最大位置权重(maxGRPW)进行对比研究。Patterson 110问题集从实践中收集而来,有10个问题包含51个活动,3种可用资源;8个问题包含的活动数量少于20个,1~3种可用资源;其它102个问题包含的活动数介于20~35之间,1~3种可用资源。
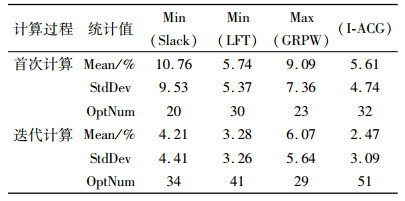
3.2 计算结果统计与比较采用Matlab语言进行编程,统计每种优先规则计算方法获得的完工期与最优完工期之间的平均偏离率(Mean),偏离标准方差(StdDev)及获得最优工期的次数(OptNum)。公平起见,对其它优先规则也进行了迭代运算,结果见表 1。
| 表 1 Patterson110问题求解结果统计 Tab. 1 statistic calculation results of Patterson 110 problems |
从上表中看到,针对Patterson110问题集,在首次结算结果中,迭代重心法计算结果与最小最迟开始时间得到的最优计划次数接近,但是与最优计划工期偏离均值与标准差均小于后者;同时这2种优先规则的计算结果明显优于最小时差和最大位置权重法计算结果。
对各种方法进行迭代计算后,计算结果都得到了优化,迭代重心法在3项指标上的结果都显著优于其它方法。
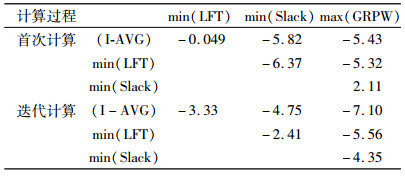
对本文方法与其它方法得到的优化工期,做基于成对数据的单边t检验,显著性水平0.05,样本值110,t0.05(109)=1.659。结果如表 2所示。
| 表 2 不同方法间的计划工期假设检验计算结果 Tab. 2 Hypothesis test results between different method |
从检验结果看到,不论是首次计算还是经正、反向迭代计算后,I-ACG计算结果均优于其它方法。当然,经过迭代计算后,结果的显著性大大提高。
经典RCPSP问题以最小化项目工期为目标,由式(1)看到,活动的重心ACG由2倍的活动最早开工时间ES,总时差TF和活动工期的和构成,前两者为时间特性参数,工期为活动属性参数,ACG包含的信息量较其它优先规则丰富。其次,新设计方法将每次迭代的计算结果都传递到下一次迭代中,使得活动的优先值具有动态性。优先规则信息的丰富性和活动优先值的动态性赋予了I-ACG方法较好地计算结果。
经统计,110个问题中,只有23个问题是在一个方向的迭代中得到最(近)优计划,需要再次利用右移、或者左移计算来求得对应的最晚、最早资源可行计划;其它87个问题可以同时得到最早、最晚资源可行计划,对比每个活动的最早开始时间与最晚开始执行时间,即可得到关键链。
4 结论在2个平行工序顺序化重心定理的启发下,本文构建了两阶段关键链识别的启发式算法,第一阶段利用活动的重心作为优先规则,运用正、反向迭代技术建立了求解RCPSP问题的迭代重心法(I-ACG);第二阶段在第一阶段得到的最优或者近优计划基础上,根据迭代计算的不同结果,运用活动的时间参数对比、或者动态规划的方法识别出关键链。
以Patterson110问题集为样本,对I-ACG法和经典的3种优先规则进行了计算结果对比,统计数据说明本文建立的启发式求解RCPSP问题的迭代重心法有一定的先进性。而且经过正、反向迭代计算,约80%的问题可以同时在两个计算方向得到最优(近优)解,极大地简化了关键链的识别过程。
当然,利用优先规则建立的启发式求解RCPSP问题的方法不能同元启发式方法和精确算法相比较,但基于优先规则建立的启发式算法省时,难度低,易应用于商业软件并被企业采纳,市场推广度好;因此不断完善和挖掘好的优先规则,建立简单实用的RCPSP问题求解方法仍具有现实意义;尤其在迭代计算中大部分问题可以同时在两个计算方向得到最(近)优解,一次计算即可达到关键链识别的目的。
| [1] |
HERROELEN W, DE REYCK B, DEMEULEMEESTER E. Resource-constrained project scheduling:A survey of recent development[J].
Computers and Operations Research, 1998, 25(4): 279-302.
DOI: 10.1016/S0305-0548(97)00055-5. |
| [2] |
BRUCKER P, DREXL A, MOHRING R, et al. Resource-constrained project scheduling:Notation, classification, models and methods[J].
European Journal of Operational Research, 1999, 112(1): 3-41.
DOI: 10.1016/S0377-2217(98)00204-5. |
| [3] |
LEACH L. Schedule and cost buffer sizing: How to account for the bias between Project performance and your model[J].
Project Management Journal, 2003, 34(2): 34-47.
DOI: 10.1177/875697280303400205. |
| [4] |
TUKEL O I, ROM W O, EKSIOGLU S D. An investigation of buffer sizing techniques in critical chain scheduling[J].
European J of Operational Research, 2006, 172(2): 401-416.
DOI: 10.1016/j.ejor.2004.10.019. |
| [5] |
莫巨华. 基于关键链的项目调度模型与算法[D]. 沈阳: 东北大学信息科学与工程学院, 2005: 16-34.
MO Juhua. Critical chain based models and algorithms for project scheduling[D]. Shenyang: College of Information Science and Engineering, Northeastern University, 2005: 16-34. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y817395 |
| [6] |
田文迪, 崔南方. 关键链项目管理中关键链和非关键链的识别[J].
工业工程与管理, 2009, 14(2): 88-93.
TIAN Wendi, CUI Nanfang. Identifying the critical chain and non-critical chain in the project management[J]. Industrial Engineering and Management, 2009, 14(2): 88-93. |
| [7] |
RABBANI M, GHOMI S M T, JOLAI F, et al. A new heuristic for resource-constrained project scheduling in stochastic networks using critical chain concept[J].
European Journal of Operational Research, 2007, 176(2): 794-808.
DOI: 10.1016/j.ejor.2005.09.018. |
| [8] |
管在林, 马力, 何敏, 等. 基于贡献度的项目调度方法研究[J].
计算机集成制造系统, 2008, 14(12): 2431-2435.
GUAN Zailin, MA Li, HE Min, et al. Project scheduling method based on the contribution index[J]. Computer Integrated Manufacturing System, 2008, 14(12): 2431-2435. |
| [9] |
马国丰, 尤建新, 杜学美. 识别关键冲突任务的定量分析[J].
上海交通大学学报, 2006, 40(4): 668-671.
MA Guofeng, YOU Jianxin, DU Xuemei. Quantitative analysis of identifying critical conflict tasks[J]. Journal of Shanghai Jiaotong University, 2006, 40(4): 668-671. |
| [10] |
HARTMANN S, BRISKORN D. A survey of variants and extensions of the resource-constrained project scheduling problem[J].
European Journal of Operational Research, 2010, 207(1): 1-14.
DOI: 10.1016/j.ejor.2009.11.005. |
| [11] |
KOLISH R. Serial and parallel resource constrained project scheduling methods revisited:theory and computation[J].
European Journal of Operational Research, 1996, 90(2): 320-333.
DOI: 10.1016/0377-2217(95)00357-6. |
| [12] |
KLEIN R. Bidirectional planning:improving priority rule-based heuristics for scheduling resource-constrained projects[J].
European Journal of Operational Research, 2000, 127(3): 619-638.
DOI: 10.1016/S0377-2217(99)00347-1. |
| [13] |
ZDAMAR L, ULUSOY G. An iterative local constraints based analysis for solving the resource constrained project scheduling problem[J].
Journal of Operations Management, 1996, 14(3): 193-208.
DOI: 10.1016/0272-6963(95)00015-1. |
| [14] |
LI K Y, WILLS R J. An iterative scheduling technique for resource-constrained Project scheduling[J].
European Journal of Operational Research, 1992, 56(3): 370-379.
DOI: 10.1016/0377-2217(92)90320-9. |
| [15] |
VALLS V, BALLESTIN F, QUINTANILLA S. Justification and RCPSP:a technique that pays[J].
European Journal of Operational Research, 2005, 165(2): 375-386.
DOI: 10.1016/j.ejor.2004.04.008. |
| [16] |
乞建勋, 李星梅, 王强.CPM网络中的路长定理及其在顺序优化中的应用[M].北京:科学出版社, 2008.
|
| [17] |
KOLISCH R. Efficient priority rules for the resource-constrained project scheduling problem[J].
Journal of Operations Management, 1996, 14(3): 179-192.
DOI: 10.1016/0272-6963(95)00032-1. |
| [18] |
HARTMANN S, KOLISCH R. Experimental evaluation of state-of-the-art heuristics for the resource-constrained project scheduling problem[J].
European Journal of Operational Research, 2000, 127(2): 394-407.
DOI: 10.1016/S0377-2217(99)00485-3. |
| [19] |
KOLISCH R, HARTMANN S. Experimental investigation of heuristics for the resource-constrained project scheduling:an update[J].
European Journal of Operational Research, 2006, 174(1): 23-37.
DOI: 10.1016/j.ejor.2005.01.065. |
| [20] |
BRUCKER P, KUST S. Complex Scheduling[M], 2006, Springer.
|
| [21] |
ÖZDAMARL, ULUSOYG. An iterative local constrained based analysis for solving the resource constrained project scheduling problem[J].
Journal of Operations Management, 1996, 14(3): 193-208.
|
 2016, Vol. 19
2016, Vol. 19