2. 重庆大学 现代物流重庆市重点实验室,重庆 400030
2. Chongqing Key Laboratory of Logistics, Chongqing University, Chongqing 400030, China
高科技产品是用于销售的技术含量和附加值高的一大类产品[1],如iPhone手机、平板电脑以及iWatch智能手表、小米手环等。这类产品有下列特点:1)生命周期不经过完整4个阶段,只经历一个比较短的时期,就快速成长并进入成熟期,基本无衰退期,整个生命周期很短。据人民网调查,都市白领现用手机平均使用期为7.35个月[2]。2)产品附加值比较高[1, 3]。如服务器类产品,除连接网络和保证运行以外,还可以辅助企业管理,降低成本,即增加了产品附加价值。
高科技产品生命周期的特点决定了它的市场需求呈现斜坡规律,即市场需求率是时间的分段函数,第1阶段随时间快速增长,第2阶段需求基本稳定(可视为常数)。在需求高速增长阶段,由于产品生产、运输和销售不平衡,产品可能缺货。此时,不少顾客不愿意等待购买,而有的顾客由于对企业忠诚或认为高科技产品附加价值或性价比高而选择等待购买,即出现销售中的短缺量滞后供给现象。许多学者对高科技产品的库存或订货策略进行了研究,如Skouri等[4]、徐贤浩等[5]、Ahmed等[6]、Agrawal等[7]、王道平等[8]、吴严亮等[9]。在这些文献中,一般把滞后供给分数看作常数(文献[7]、[9]),或认为滞后供给分数只与某一因素如时间(文献[4]、[6]、[8])或价格折扣(文献[5])有关。然而高科技产品的滞后供给分数与多个因素相关。一是与等待时间有关系,时间短一些,愿意等待的顾客就越多;而一些顾客却更看重产品价格高低或附加价值大小,削减价格就相当于增加了产品附加价值。因此,高科技产品在缺货时的顾客等待意愿主要取决于时间和产品价格。近年来已有一些学者建立了多因素影响短缺量滞后供给的库存模型,如Duan等[10]建立了滞后供给分数与顾客等待时间和缺货量均相关的库存模型,徐贤浩等[11]建立了滞后供给分数与消费者创新系数和模仿系数都相关的库存模型,罗兵等[12]建立了一个存货影响销售下顾客等待的特价商品经济订货批量模型,罗兵等[13]又在文献[12]基础上,建立了交叉销售下价格和存货影响需求的特价商品EOQ模型,但文献[10-13]未考虑高科技产品生命周期斜坡需求的特点,并且顾客也只包括低收入群体,而实际上其他收入群体同样购买高科技产品。
以上分析表明,高科技产品的市场需求呈现斜坡变化规律,产品缺货时顾客的等待意愿主要受时间和价格的影响,目前对这方面的研究不多。本文正是考虑高科技产品斜坡需求和延迟补货的特点,将文献[12]-[13]的市场群体扩展为价格偏好者(低收入顾客)和时间偏好者(高收入顾客),构造2种不同的延迟函数,通过建立数学模型和数值仿真,分析主要参数变化时对高科技产品订货策略和总利润的影响,为销售商经营决策提供依据。
1 假设条件和符号定义参考文献[5],给出高科技产品市场需求率为: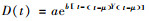
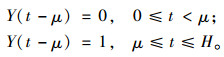
|
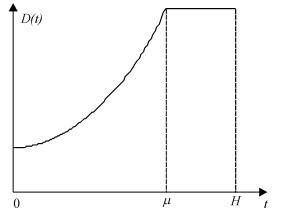
其中,H为产品计划期长度,μ为产品需求增长期长度。产品的市场需求率变化如图 1所示。
|
图 1 高科技产品市场需求率变化图示 Fig. 1 The change graph of high-tech products demand rate |
高科技产品在成长阶段,市场需求增长很快。但由于供应商生产或运输等原因可能导致产品缺货,并延长一定时间补充存货,此时丢失部分顾客,一些顾客对企业忠诚或认为产品附加价值高而愿意等待购买。在此将等待顾客分为价格偏好者和时间偏好者,其中α为价格偏好者的比例,0≤α≤1,1-α为时间偏好者的比例。定义2种顾客的延迟函数如下:ρp为价格偏好者的延迟函数,ρp=kpe-k1p,其中0≤ρp≤1,kp为价格偏好者的延迟补货敏感因子,p为产品销售价,k1为价格偏好者的价格敏感因子(简称价格敏感因子);ρτ为时间偏好者的延迟函数,ρτ=kte-k2τ,其中0≤ρτ≤1,kt为时间偏好者的延迟补货敏感因子,τ为顾客等待时间,k2为时间偏好者的时间敏感因子(简称时间敏感因子)。
其他条件和符号定义如下:Ti-1为第i周期开始缺货时刻点,ti为第i周期补货时刻点(决策变量),瞬时补货,提前期为零,[Ti-1, Ti]为一个订货周期,T为订货周期长度(各周期相同),i=1, 2, ……, n;n为订货次数(决策变量),H=nT;Ii(t)为第i周期t时刻库存水平;λi为第i周期服务水平,λi=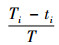
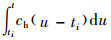
产品在计划时间内库存状态变化如图 2所示。

|
图 2 产品在计划时间内的库存水平变化图示 Fig. 2 The change graph of inventory level of high-tech products in its horizon |
产品在第i周期t时刻的库存水平需满足以下等式:
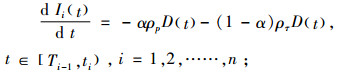
|
(1) |
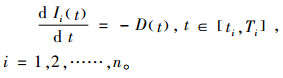
|
(2) |
其中,
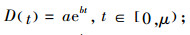
|
(3) |
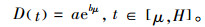
|
(4) |
根据边界条件:Ii(Ti)=0, i=1, 2, ……, n,求解式(1)、(2)可得:
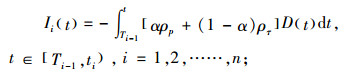
|
(5) |
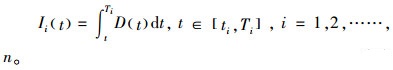
|
(6) |
由式(5)可得第i周期最大延迟补货量Bi为
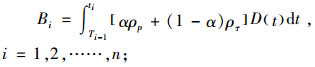
|
(7) |
由式(6)可得第i周期最大库存量Si为
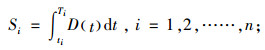
|
(8) |
由式(7)和(8)可得第i周期订货量Qi为
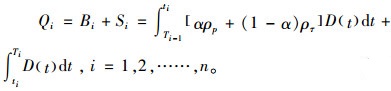
|
(9) |
第i周期产品销售收入、成本和总利润贴现值计算如下。
1) 销售收入TRi:
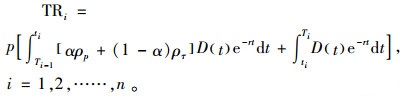
|
(10) |
2) 采购成本Cbi:
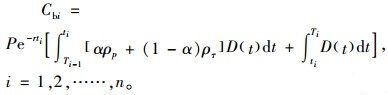
|
(11) |
3) 订货成本c0i:
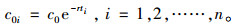
|
(12) |
4) 保管成本Chi:
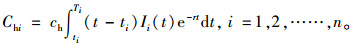
|
(13) |
5) 延迟补货成本Csi:
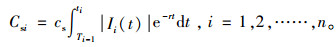
|
(14) |
6) 丢单成本Cli:
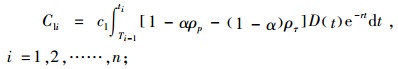
|
(15) |
7) 总利润TPi(ti):
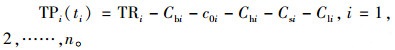
|
(16) |
因此,可以列出产品在计划时间内总利润TP(n, ti)为
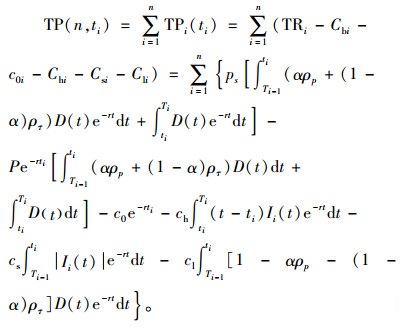
|
(17) |
根据式(17),建立优化模型如下。
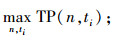
|
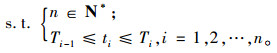
|
(18) |
参考文献[5]、[17],设定基本参数如下:a=6,b=0.05,r=0.2, α=0.6,μ=8,H=10,kp=0.9,k1=0.000 5,kt=0.8,k2=0.6,p=1 360,P=750,c0=1 200,ch=120,cs=26,cl=30。使用Mathematica 9.0版本工具软件进行模拟计算,计算过程和结果如表 1。最优订货次数n*=6;各周期最优订货时刻点:t1*=0.543,t2*=2.203,t3*=3.864,t4*=5.526,t5*=7.188,t6*=8.829;最大总利润TP*=10 321.300。
| 表 1 数值算例表1) Tab. 1 Calculation example |
以下对主要参数进行灵敏度分析,基本数据与3.1节算例相同。
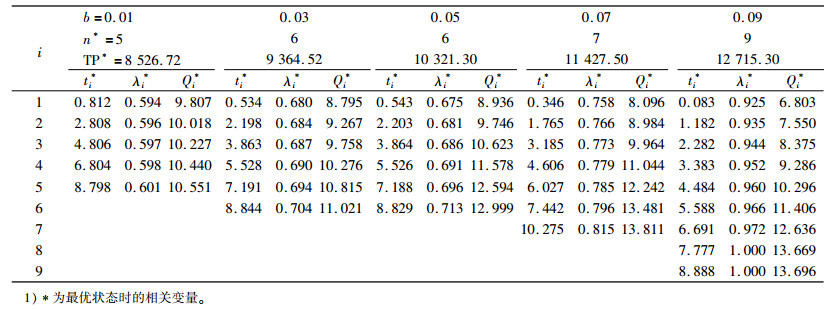
表 2说明,b增大时,订货次数和服务水平增加,订货量大致减少,总利润增加。由于b增大时,需求量增多,订货次数增加,2种因素平衡使订货量减少;市场需求量增加要求缩短缺货时间,提高服务水平;另外,总利润增加是因为使总利润增加的因素(如需求量增加等)大于减少的因素(如订货成本增加等)。
| 表 2 需求增长因子b的灵敏度分析1) Tab. 2 The sensitivity analysis of demand growth factor b |
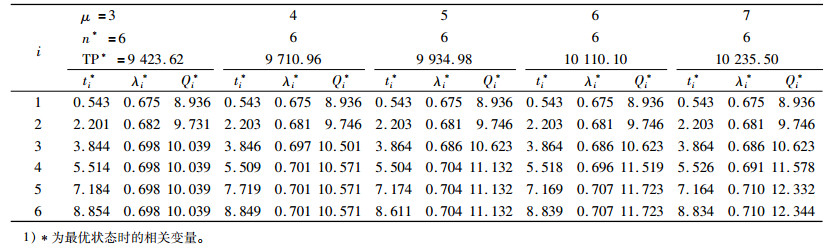
表 3说明,μ增大时,订货次数不变,各周期服务水平和订货量在前几个周期不变,后几个周期略有提高或增加,总利润增加。由于μ增大时,需求量增多使订货次数增加,和降低订货成本平衡使订货次数不变;另外,μ增大时使需求率在前几个周期增长缓慢或基本不变,导致服务水平和订货量无变化,而后几个周期有一定提高或增加;总利润增加是因为使总利润增加的因素(如需求量增加等)大于减少的因素(如保管成本增加等)。因此,当需求增长期长度增大时,销售商应不改变订货次数以及前几个周期的服务水平和订货量,但应该提高后几个周期的服务水平和订货量。
| 表 3 产品需求增长期长度μ的灵敏度分析1) Tab. 3 The sensitivity analysis of demand growth length μ |
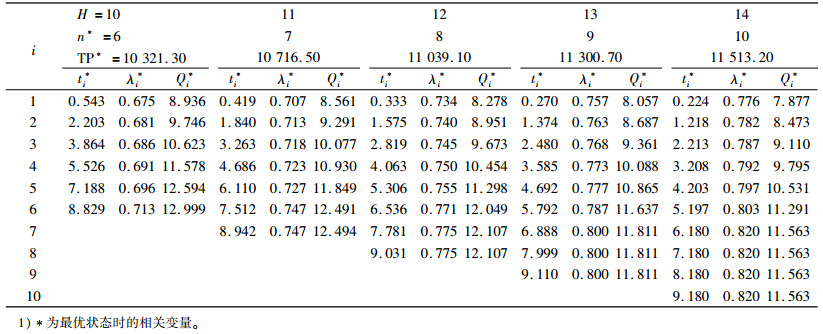
表 4说明,H增大时,订货次数和服务水平增加,订货量减少,总利润增加。由于计划时间增大时,需求量增加,订货次数增加,2种因素平衡使订货量减少;需求量增加要求缩短缺货时间,提高服务水平;总利润增加是因为使总利润增加的因素(如需求量增加等)大于减少的因素(如订货成本增加等)。
| 表 4 产品计划期长度H的灵敏度分析1) Tab. 4 The sensitivity analysis of planning horizon length H |
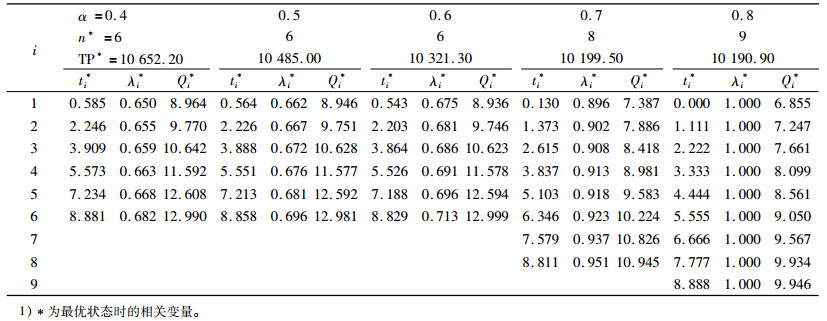
表 5说明,α增大时,订货次数和服务水平增加,订货量和总利润减少。由于价格偏好者比例α增大时,会有更多顾客愿意等待购买,延迟补货量增加,丢单量减少,市场需求量增加,订货次数增加,2种因素平衡使订货量减少;市场需求量增加要求缩短缺货时间,提高服务水平;总利润减少是因为使总利润增加的因素(如需求量增加等)小于减少的因素(如订货成本增加等)。
| 表 5 价格偏好者比例α的灵敏度分析1) Tab. 5 The sensitivity analysis of price preference customers α |
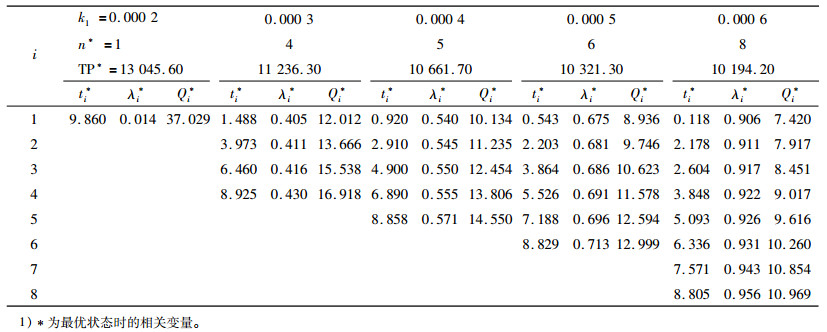
表 6说明,k1增大时,订货次数和服务水平增加,订货量减少,总利润减少。由于k1增大时,价格偏好者延迟数量减小,丢单数量增加,这就要求减少缺货时间和保管成本等来冲抵丢单成本,因此需要减少订货量,增加订货次数;总利润减少是因为使总利润增加的因素(如保管成本减少等)小于减少的因素(如丢单成本增加等)。另外,时间敏感因子k2的灵敏度分析与价格敏感因子k1基本相同,这里不再赘述。
| 表 6 价格敏感因子k1的灵敏度分析1) Tab. 6 The sensitivity analysis of price sensitive factor k1 |
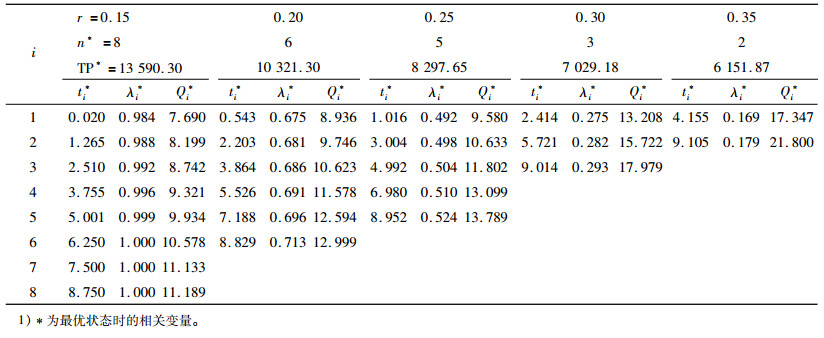
表 7说明,r增大时,订货次数和服务水平减少,订货量增加,总利润减少。由于r增大时,订货次数减少,资金投入量减少,增加订货量,降低服务水平;总利润减少是因为使总利润增加的因素(如订货成本减少等)小于减少的因素(如保管成本增加等)。
| 表 7 资金贴现率r的灵敏度分析1) Tab. 7 The sensitivity analysis of discount rate r |
考虑高科技产品市场需求和延迟补货的特点,通过建立数学模型和仿真分析,研究了系统主要参数对销售商订货策略和总利润的影响,得到下列结论:需求增长因子、价格敏感因子以及资金贴现率对订货次数和服务水平的影响比其它因素大;产品需求增长期长度、价格偏好者比例对服务水平的影响比订货次数大;计划期长度对服务水平的影响比订货次数小。当需求增长因子、计划期长度、价格偏好者比例以及价格敏感因子增大时,应增加订货次数,提高服务水平,减少订货量;当需求增长期长度增大时,订货次数以及前几个周期服务水平和订货量不变,应提高后几个周期的服务水平和订货量;当资金贴现率增大时,应减少订货次数和服务水平,增加订货量。
| [1] |
百度百科. 高科技产品[EB/OL]. (2015-06-13)[2015-10-13]http://baike.baidu.com/view/3529788.htm?fr=aladdin
|
| [2] |
人民网. 机构调查显示: 白领平均每7. 35个月更换新手机[EB/OL]. (2013-05-25)[2016-03-07]http://finance.people.com.cn/n/2013/0525/c70846-21611797.html
|
| [3] |
李尚鹏. 基于多项Logit选择的易逝性高科技产品上市策略研究[D]. 湖南: 湖南大学, 2014.
LI Shangpeng. Research of the perishable high-tech product launch strategy based on the multinomial logit choice[D]. Hunan: Hunan Normal University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10532-1014311401.htm |
| [4] |
SKOURI K, KONSTANTARAS I, PAPACHRISTOS S, et al. Inventory models with ramp type demand rate, partial backlogging and Weibull deterioration rate[J].
European Journal of Operational Research, 2009, 192(1): 79-92.
DOI: 10.1016/j.ejor.2007.09.003. |
| [5] |
徐贤浩, 蔡成元, 沈古文. 基于可控提前期和延迟供货的短生命周期产品库存模型[J].
中国管理科学, 2010, 18(2): 42-47.
XU Xianhao, CAI Chengyuan, SHEN Guwen. A deterministic inventory model for short-life cycle products with variable lead time and backorder discount considerations[J]. Chinese Journal of Management Science, 2010, 18(2): 42-47. |
| [6] |
AHMED M A, AL-KHAMIS T A, BENKHEROUF L. Inventory models with ramp type demand rate, partial backlogging and general deterioration rate[J].
Applied Mathematics and Computation, 2013, 219(9): 4288-4307.
DOI: 10.1016/j.amc.2012.09.068. |
| [7] |
AGRAWAL S, BANERJEE S, PAPACHRISTOS S. Inventory model with deteriorating items, ramp-type demand and partially backlogged shortages for a two warehouse system[J].
Applied Mathematical Modelling, 2013, 37(20/21): 8912-8929.
|
| [8] |
王道平, 陈丽, 杨岑. 基于Weibull函数的易逝品库存优化模型研究[J].
工业工程与管理, 2014, 19(5): 1-6.
WANG Daoping, CHEN Li, YANG Cen. Study on optimized inventory model of perishable products based on Weibull function[J]. Industrial Engineering and Management, 2014, 19(5): 1-6. |
| [9] |
吴严亮, 张人千, 方卫国. 考虑产品租赁与缺货损失的制造商最优营销策略[J].
工业工程, 2015, 18(2): 41-50.
WU Yanliang, ZHANG Renqian, FANG Weiguo. Optimal marketing strategy for a manufacturer considering product leasing and lost sales[J]. Industrial Engineering Journal, 2015, 18(2): 41-50. |
| [10] |
DUAN Y R, LI G P, TIEN J M, et al. Inventory models for perishable items with inventory Level dependent demand rate[J].
Applied Mathematical Modelling, 2012, 36(10): 5015-5028.
DOI: 10.1016/j.apm.2011.12.039. |
| [11] |
徐贤浩, 陈雯, 廖丽平, 等. 基于需求预测的短生命周期产品订货策略研究[J].
管理科学学报, 2013, 16(4): 22-32.
XU Xianhao, CHEN Wen, LIAO Liping, et al. Ordering strategy of life-cycle products based on the demand forecasting[J]. Journal of Management Science in China, 2013, 16(4): 22-32. |
| [12] |
罗兵, 王晶晶, 常旭华. 存货影响销售和顾客等待的特价商品EOQ模型[J].
系统工程学报, 2013, 28(3): 37-46.
LUO Bing, WANG Jingjing, CHANG Xuhua. An EOQ model for off-price merchandise with stock-dependent selling rate and waiting behavior of customers[J]. Journal of Systems Engineering, 2013, 28(3): 37-46. |
| [13] |
罗兵, 冯璐, 陈星岐. 交叉销售下价格和存货影响需求的特价商品经济订货批量模型[J].
系统工程理论与实践, 2014, 34(4): 826-835.
LUO Bing, FENG Lu, CHEN Xingqi. Economic order quantity model for off-price merchandise with demand depends on selling price and stock under cross-selling[J]. Systems Engineering-Theory & Practice, 2014, 34(4): 826-835. DOI: 10.12011/1000-6788(2014)4-826. |
| [14] |
MOON I, GIRI B C, KO B. Economic order quantity models for ameliorating/deteriorating items under inflation and time discounting[J].
European Journal of Operational Research, 2005, 162(3): 773-785.
DOI: 10.1016/j.ejor.2003.09.025. |
| [15] |
SARKAR B, MOON I. An EPQ model with infiation in an imperfect production system[J].
Applied Mathematics and Computation, 2011, 217(13): 6159-6167.
DOI: 10.1016/j.amc.2010.12.098. |
| [16] |
MONDAL M, MAITY A K, MAITI M K, et al. A production-repairing inventory model with fuzzy rough coefficients under inflation and time value of money[J].
Applied Mathematical Modelling, 2013, 37(5): 3200-3215.
DOI: 10.1016/j.apm.2012.07.024. |
| [17] |
罗兵, 冯晖, 陈星岐. 新鲜度、价格和库存水平影响需求的高科技农产品订货策略[J].
科技管理研究, 2015, 35(10): 222-226.
LUO Bing, FENG Hui, CHEN Xingqi. The ordering policy of High-tech products affected by freshness, price and inventory level[J]. Science and Technology Management Research, 2015, 35(10): 222-226. DOI: 10.3969/j.issn.1000-7695.2015.10.043. |
 2016, Vol. 19
2016, Vol. 19