2. 重庆科技学院 法政与经贸学院,重庆,401331;
3. 国网重庆市电力公司 电力科学研究院,重庆,400015
2. School of Politics and Trade, Chongqing University of Science and Technology, Chongqing 401331, China;
3. Electric Power Research Institute, State Grid Chongqing Electric Power Company, Chongqing 400015, China
作为一种清洁能源利用方式,电动汽车在全球多个国家和地区发展迅猛。与此对应的充电服务配套基础设施建设也开始陆续展开,PPP模式在电动汽车充电服务市场的投资与融资中受到社会普遍关注。PPP(public-private-partnership)就是政府和社会投资者以特许经营权协议为纽带,以双方收益和风险共享为原则而建立的一种长期合作投融资模式[1-2]。通常,由社会投资者负责设计与建设,并承担建成后的经营管理与维修保护,通过项目的运营收费以及政府的补贴或付费而获得合理的投资回报。目前,PPP模式在电动汽车充电服务基础设施建设中,如充换电站的建设中已经出现广泛的应用[3]。
已有的参考文献表明,电动汽车充电电价是国内外研究者关注的重点,如电动汽车充电电价对充电站投资成本的影响[3]、电动汽车充电对电网安全性与可靠性的冲击[4]。尤其是电动汽车充电与电网运行中的削峰填谷[5],有Zhang等[6]和Andersen等[7]将电价与配电网容量市场的容量分配联系起来,O’Connell等[8]研究了由于电动汽车充电造成电网拥堵所带来的成本增加和电价的变化。Li等[9]的研究集中于探索了市场参与者(包括运营商和电动汽车用户)的行为,对充电电价的影响,He等[10]研究了充电电价的2个影响因素,即输配电网在充电服务中的网损成本,以及电动汽车由于交通网络产生的时间价值。综合国内外的情况,已有的研究主要关注于电动汽车充电的充电技术与电网的成本影响方面[11],而从市场主体的行为来研究电动汽车的充电电价,特别是充电服务定价的文献较少。
充电服务费和电网输配电价是电动汽车充电电价的两个组成部分,国内不同地方的电动汽车充电电费水平差异较大。出于国家电动汽车产业的扶持政策,电动汽车充换电实施用电优惠的电价政策。鉴于各地电动汽车的发展状况不同,充电电价按照电网企业的总体规划要求,实行分类指导定价,充电服务价格各地先自行试点,并没有具体要求。以国家电网重庆电力公司为例,电动汽车充电电价暂定为1元/kWh,包括输配电价0.828元和充电服务费0.172元两部分,其中0.828元的输配电价部分,随电网销售电价联动调整。
充电服务费是由充电站收取,属于充电服务运营商的收入,但充电服务费的定价一直缺乏合理的定价依据。本文将针对这一问题,研究如何对充电运营服务定价,才能均衡相关部门利益,实现多方利益协调,从而推动电动汽车规模化发展。
1 基于PPP模式的电动汽车充电服务市场PPP模式在政府的公共支出政策中有着很重要的作用。首先,通过政策扶持以使私人投资者获取合理收益,是吸引民间资本进入的前提[12]。从各国电动汽车发展的实践来看,由于已有电网的改造和新的充电设施建设,造成充电成本较高。而电动汽车充电市场需求具有较大的不确定性和用电的不稳定性[11],沿用目前的电价体系,会导致充电服务价格偏高,导致电动汽车用户的使用成本超过其承受能力,难以推动电动汽车的普及和充电服务市场的发展。因此政府政策的引导和支持作用必不可少。其次,政府可以在PPP模式下,通过引入市场竞争,来提高公共品市场的供给效率[13],在电动汽车充电服务市场的形成与发展中,协调社会资本等利益相关主体的市场行为,实现多方利益均衡的格局。
1.1 充电服务市场参与主体在PPP模式下,电动汽车充电服务涉及政府、充电服务运营商(一般由电力公司执行)和充电用户三方主体。按照PPP模式,充电服务市场的基础设施部分,主要包括充电站、充电桩和换电站,应当由充电服务运营商和政府作为投资主体,共同建设完成;充电服务的管理主要由运营商进行,而服务对象是电动汽车充电用户。
假定在充电服务市场中,市场需求量Q,充电服务价格为p,二者关系可用函数表述为
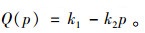
|
(1) |
其中,k1,k2>0,设电动汽车保有量为N,且电动汽车平均单车年充电电力需求量为θ时,有Q=Nθ。
1) 运营商收益。
充电服务运营商的年平均运营成本CO,包括充电设施建设成本折旧和运营成本两部分,设
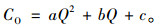
|
(2) |
其中a,b>0,表明CO随Q的增加而增加,c是CO中的固定成本部分。
充电服务运营商者年利润RO等于综合充电服务收入(p×Q)与平均成本CO的差额,则有
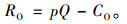
|
(3) |
2) 消费者剩余。
汽车用户选择电动汽车和传统汽车主要依据是持有成本,政府补贴在于鼓励电动汽车的使用。假定政府根据电动汽车市场化发展水平确定对充电用户进行补贴,设补贴额度为B(Q)是关于Q的函数,与电动汽车用户的用电量相关。
用户对充电综合服务的支付意愿T最低为Tmin、最高为Tmax,其值需要通过市场调研获得,该数据会随着充电服务需求而变化。平均一年中电动汽车用户的消费者剩余RC可表示为支付意愿与实际支出成本的差额,有
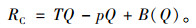
|
(4) |
3) 政府收益。
政府的目标主要是使全社会各主体的经济收益和环境效益最大化,为此通过提供公共产品和服务来达到资源配置最优化的目的。电动汽车的发展,假定带来的外部效应为RG,其效益并不能由电动汽车市场的参与者得到,而是全社会共享;燃油改为充电后,假定每度电碳减排的价值为VA,则
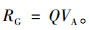
|
(5) |
社会总效益包括各方经济利益和外部环境收益的总和RT,故基于全社会总效益的政府收益目标函数可表述为
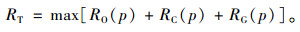
|
(6) |
PPP模式下,政府与企业合作建设充电基础设施,降低运营商建设运营风险;同时也通过对定价权规制、补贴政策等多种手段,以此影响投资者提供电动汽车充电服务能收取的最高价和最低价,从而实现对市场的间接调控。
电动汽车市场发展的不同时期,政府或充电服务运营商可能分别充当了充电服务定价权的主导者。不同主体定价目的是不一样的,政府考虑的是消费者和企业剩余、经济利益、环境目标等社会总收益;运营商考虑的是企业利益最大化。而决定定价权归属的主体是电动汽车充电用户。于是不同的电动汽车发展阶段,充电服务市场中的定价权是变动的,也就决定了定价模型是个动态的模型。
在电动汽车发展的不同时期,充电服务市场的需求程度也会出现不同,参考文献[1, 14-15]等的研究,本文根据充电服务的需求程度差异,将充电服务市场划分为高、中、低3种不同需求情景,以此进行研究。
2 不同需求情景下的电动汽车充电服务定价模型本文根据电动汽车发展的不同阶段,随着电动汽车保有量的变化,将充电服务市场根据需求的变化,划分为高、中、低3种情景进行分析。
2.1 低需求的充电服务市场通常在市场初期,为激励电动汽车的运用,充电服务定价应该以政府管制为核心。这时电动汽车保有量规模较小,充电服务商的平均成本CO大于消费者支付意愿T(考虑燃油汽车持有成本和电动汽车购置成本),充电服务需求极低。为鼓励电动汽车发展,拉动充电服务需求,政府实行用户充电电价补贴以提高消费者支付意愿。政府根据充电服务电价p与网络平均成本差价CO进行补贴,此时补贴为B(p)=(p-Tmax)Q。该情景下政府制定电动汽车保有量规划,如果电动汽车正常运行,则实际是确定了充电服务需求量,该情景符合Stackelberg博弈模型。属于政府先行动,做出最优Q决策之后,运营商跟随其后行动。
政府的价格管制在低需求的充电服务市场定价中将发挥主导作用。这一阶段政府需要保证充电服务运营商的持续经营,不能亏损破产,同时也要调动电动汽车消费者的积极性,其目标函数如式(6)所示。
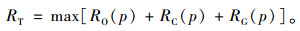
|
(7) |
同时,式(7)必须满足
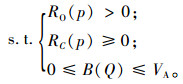
|
将上式的目标最优化,根据一阶导数为零,求解可得最优充电量为
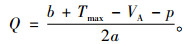
|
(8) |
在政府确定电动汽车发展目标Q后,则充电服务运营商将根据自身利益最大化确定服务价格,其目标函数为
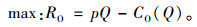
|
(9) |
将式(8)带入求式(9),得最优充电服务定价为
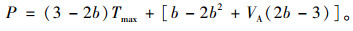
|
(10) |
由式(10)可得,在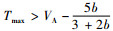
电动汽车的保有量随着市场的发展而增长,当市场发展到一定规模后,充电运营边际成本高有所下降,导致定价高于消费者最低支付意愿,即Tmax>p>Tmin。此时充电服务按市场供需自由竞争,充电服务定价权交给市场。此时市场需求函数为式(1),充电用户补贴为零,充电服务运营商的目标函数依然为式(9),根据极值条件,求解得出此时定价为
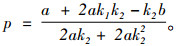
|
(11) |
从充电运营商的最优定价策略(11)可以看出,在中度需求的充电服务市场中,运营商的充电服务价格与市场的充电需求弹性k2成反比,即k2越大,定价越低;反之,k2越小,定价就越高。
2.3 高需求的充电服务市场当充电服务市场规模进一步扩大。达到规模效应的时候,充电服务商的边际成本会进一步降低,甚至低于电动汽车用户的最低支付意愿,即p<Tmin时,市场将按照运营商的定价进行交易,但是运营商并没有考虑环境的外部性,政府目标如果是福利最大化,在需要限定最低交易价格,市场按照政府规制最低价进行交易。政府目标函数为式(6),政府不再给予补贴,此时B=0。
易求解得到此时市场定价模型为
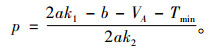
|
(12) |
由式(12)可得,对于具有规模效应的充电服务市场,当0<Tmin<2ak1-b-VA时,政府对充电服务将制定最低限价,防止充电服务市场的过度发展,除了有利于保护市场的有序竞争和良性循环外,还有利于保护环境,使碳减排带来的外部性RG与充电服务定价有机地结合起来。式中,VA的值越大,表明外部性效应RG越大,整个社会的效用就越大,充电服务最低定价也就越低,反之,最低定价就会越高。
3 不同市场需求情景下的定价模型分析运用充电服务定价模型,研究电动汽车发展的不同阶段,对比不同充电服务市场需求状况,可以得出以下结论。
1) 在电动汽车发展初期,受充电服务成本、市场需求状况、外部环境因素影响,政府应当有利于充电运营商的持续经营和调动电动汽车用户积极性两方面来培育市场,对运营商采取最高限价,对电动汽车消费者实施补贴。
当充电服务市场达到规模效应,并且充电服务运营商的边际成本低于电动汽车用户的最低支付意愿时,政府应该采取最低限价措施,确保充电服务市场的有序竞争和市场发展带来的外部性正效应的最优化。
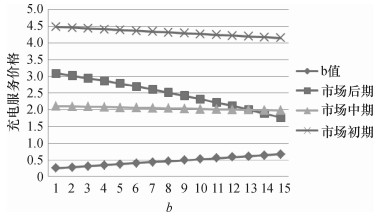
2) 政府为电动汽车充电服务确定的规制价格,最高与最低限价范围,与PPP模式中服务运营商的边际成本参数b值紧密相关。为此,模拟充电服务市场的运营,设定边际成本参数,计算此时对应的最终定价,可得到二者之间相应的数据,其模拟结果见图 1。
|
图 1 不同发展阶段的b值与充电服务定价水平的关系 Fig. 1 The value of b according to the prices of charging service in different stages |
图 1是根据重庆市电动汽车产业发展规划,模拟重庆空港充电站在运营中的充电服务价格,以及运营中成本数据和盈亏情况,在假定k1=8,k2=1.5,a=0.42,VA=0.02,Tmin=0.8,Tmax=1.2时,分别计算了电动汽车市场发展的三阶段数据。
结果显示,不同需求情景下的b值与充电服务定价水平呈反相关关系。可以看到随着规模报酬递增,充电服务运营商的成本在下降,政府的规制价格也在下降,为防止过度竞争,就需要限定最低价,以保护市场的正常发展。
4 总结全文基于PPP模式的特征,结合电动汽车充电服务特性,运用公共定价理论,分析政府和运营商的收益目标函数,采用情景分析法和Stackelberg博弈理论,分析了不同电动汽车发展情景下,政府引导电动汽车充电服务定价的机制原理,研究得出以下结论。
1) PPP模式下,政府对于电动汽车充电服务市场定价权的规制,有利于协调平衡各参与方的利益。在市场初期通过补贴分担持有者成本,并限定最高价启动市场;市场规模化之后,则通过限定电动汽车充电服务价格的最低价,防止过度竞争,保护合理利润。
2) 政府的规制定价,有利于社会福利最大化,而限价的依据主要与平均成本参数和外部环境价值。这对于电动汽车的产业化和经济发展,以及社会清洁环境机制,都有很强的外部经济性。
文章提出的基于PPP模式的电动汽车充电服务定价模型,还有待于未来实践中的检验与修正,并从理论上进一步充实完善。
| [1] |
宋波, 徐飞. 不同需求状态下公私合作制项目的定价机制[J].
管理科学学报, 2011, 8(14): 86-96.
SONG Bo, XU Fei. Analysis on the pricing mechanism of public-private partnership project with different market demand level[J]. Journal of Mangement Sciences in China, 2011, 8(14): 86-96. |
| [2] |
姚鹏程, 王松江. 双层目标规划模型在PPP项目中的应用研究[J].
中国行政管理, 2010(8): 122-125.
YAO Pengcheng, WANG Songjiang. Study on application of bilevel programming model in Public-Private-Partnership project[J]. Chinese Public Administration, 2010(8): 122-125. |
| [3] |
SCHROEDER A, TRABER T. The economics of fast charging infrastructure for electric vehicle[J].
Energy Policy, 2012, 43: 136-144.
DOI: 10.1016/j.enpol.2011.12.041. |
| [4] |
MALLETTE M, VENKATARAMANAN G. The role of plug-in hybrid electric vehicles in demand response and beyond[C]. 2010 IEEE PES Transmission and Distribution Conference and Exposition. New Orleans, LA, 2010: 1-7.
|
| [5] |
GALUS M, ANDERSSON G. Demand management of grid connected plug-in hybrid electric vehicles (PHEV)[C]. 2008 IEEE Energy 2030 Conference. Atlanta, GA, 2008: 1-8.
|
| [6] |
ZHANG Kangkang, XU Liangfei, OUYANG Minggao, et al. Optimal decentralized valley-flling charging strategy for electric vehicles[J].
Energy Conversion and Management, 2014, 78: 537-550.
DOI: 10.1016/j.enconman.2013.11.011. |
| [7] |
ANDERSEN P B, HU Junjie, HEUSSEN K. Coordination strategies for distribution grid congestion management in a multi-actor, multi-objective setting[C]//IEEE PES Innovative Smart Grid Technologies Europe Conference. Berlin, Germany: IEEE PES, 2011: 1-8.
|
| [8] |
O'CONNELL N, WU Q, φSTERGAARD J, et al. Day-ahead tariffs for the alleviation of distribution grid congestion from electric vehicles[J].
Electric Power Systems Research, 2012, 92: 106-114.
DOI: 10.1016/j.epsr.2012.05.018. |
| [9] |
LI Zhe, OUYANG Minggao. The pricing of charging for electric vehicles in China: Dilemma and solution[J].
Energy, 2011, 36: 5765-5778.
DOI: 10.1016/j.energy.2011.05.046. |
| [10] |
HE Fang, YIN Yafeng, WANG Jianhui, et al. Sustainability SI: optimal prices of electricity at public charging stations for plug-in electric vehicles[J].
Networks and Spatial Economics, 2016, 16(1): 131-154.
DOI: 10.1007/s11067-013-9212-8. |
| [11] |
葛少云, 冯亮, 刘洪, 等. 考虑车流信息与配电网络容量约束的充电站规划[J].
电网技术, 2013, 37(3): 582-587.
GE Shaoyun, FENG Liang, LIU Hong, et al. Planning of charging stations considering traffic plow and capacity constraints of distribution network[J]. Power System Technology, 2013, 37(3): 582-587. |
| [12] |
何寿奎, 孙立东. 公共项目定价机制研究-基于PPP模式的分析[J].
价格理论与实践, 2010(2): 10-11.
HE Shoukui, SUN Lidong. Public project pricing mechanism research-based on the analysis of the PPP model[J]. Journal of Price Theory & Practice, 2010(2): 10-11. |
| [13] |
唐敏, 徐解宪, 顾月蕾. 电动汽车充电站建设与运营的模式研究[J].
华东电力, 2011, 39(2): 0203-0206.
TANG Min, XU Jiexian, GU Yuelei. Research on the construction and operation mode of electric vehicle charging stations[J]. East China Electric Power, 2011, 39(2): 0203-0206. |
| [14] |
叶晓, 杨俊萍. 基于多目标规划模型的PPP项目定价方式研究[J].
统计与决策, 2012(6): 74-77.
YE Xiao, YANG Junping. PPP project pricing study Based on multi-objective programming model[J]. Journal of Statistics and Decision Making, 2012(6): 74-77. |
| [15] |
段世霞, 朱琼, 侯阳. PPP项目特许价格影响因素的结构方程建模分析[J].
科技管理研究, 2013(10): 197-201.
DUAN Shixia, ZHU Qiong, HOU Yang. Structure equation modeling of affecting factors of concession price of PPP project[J]. Science and Technology Management Research, 2013(10): 197-201. DOI: 10.3969/j.issn.1000-7695.2013.10.045. |
 2016, Vol. 19
2016, Vol. 19