近年来,农村物流成本过高、产品滞运滞销的问题日益突出。为破除这一困境,各级政府积极推进农村物流基础设施建设。物流企业则从运营管理角度来创新出一些适合农村特点的物流运作模式,如流通企业+农产品生产者物流模式、批发商+批发市场+零售物流模式、第三方物流模式[1]、农超对接模式[2]及客运班车配送等模式[3]。它们在一定程度上解决了农产品进城与工业品下乡的物流问题。其中,结合电商物流“最后一公里”配送与客运班线思想、整合便利店与货车运力资源的农村“货运班线”物流模式,是当前解决农村物流问题较为成功的尝试。从湖北省秭归县华维物流公司运营10个乡镇“货运班线”的实践来看,“货运班线”物流能有效减少农户对物流需求的不确定性,将分散的农产品通过固定班次(定时、定点、定线、定车)进行集中,实现集中运输目标,大大降低了物流成本(如图 1)。但相比于城市,农村具有地广人稀的特征,农产品供应与居民需求分布在空间上更加分散、时间上具有更大的不确定性。因此“货运班车”途径各个班线站点的集货与定价直接影响到班线运营的效果,若揽货规模不足而导致空载,最终增加物流成本而使企业亏损。因此,如何实现货运班线沿途服务点的货物集中并制定有效的物流服务价格,是农村“货运班线”是否可持续发展的关键。

|
图 1 农村“货运班线”物流线路示意图 Fig. 1 Rural "freight route" logistics routing |
物流服务区别于一般有形产品,服务定价主要与服务对象的属性密切相关,如货物重量、体积、运送距离、物流时效、货物本身的价值、物流作业难度等,因此国内外学者关于物流服务定价策略基本围绕上述属性进行研究。当第三方物流企业仅仅将物流服务作为与普通商品一样的产品时,在定价过程中采用传统的定价机制,包括成本导向定价法、客户导向定价法和竞争导向定价法[4]。其中,李济球[5]对宁波某物流企业原有运输成本的构成进行分析,针对不同的客户群,运用数学建模的方法,得出服务成本核算的差别优化模型。针对传统定价机制的局限性,已有学者将博弈论运用于第三方物流企业服务定价机制中,从而更有利于第三方物流企业为外部企业提供服务[6]。其中,谢天帅等[7-9]根据制造商与服务商自身及其所处市场的特征,应用博弈论建立了第三方物流服务定价模型,给出了不同系统状态、不同决策方式下第三方物流服务定价的均衡策略及结果。孙小清等[10]通过Bertrand博弈模型对第三方物流产业进行定价博弈分析,并对厦漳泉大都市区域内第三方物流产业进行仿真,验证了信息共享、形成价格联盟比企业盲目进行市场竞争能创造出更高效的整体效益。以上文献均是针对价格敏感型需求客户,但随着市场竞争的加剧,时间敏感需求客户群体越来越大,价格与交货期都是该类客户满意程度的关键因素。关于价格与交货期决策问题的研究,杨文胜等[11-12]探讨了市场对供应链企业响应能力具有不同评价概率时,供应链企业的交货期相关定价最优决策策略;林勇等[13]建立了引入额外费用的交货期相关定价模型,并探讨了价格确定、额外费用确定两种假设情况下模型的最优性;涂淑丽[14]在已有交货期相关定价模型的基础上,把供应链响应时间视为一种重要的可分配资源,分析不同管理模式下的供应链企业交货期定价决策;申成霖等[15]考虑了由一个制造商和两个相互竞争的零售商组成的两阶段分散式供应链系统,建立了价格和时间双敏感需求下的供应链定价与交货期联合决策模型,并给出了基于Stackelberg博弈的供应链定价和承诺交货期的最优决策;Ulku等[16]探讨了在客户对价格和时间敏感的物流市场上,使第三方物流企业利润率最大化的基于交货期的服务定价方案,包括差别定价和统一定价。
本文针对农村“货运班线”物流服务的特征,考虑客户对价格和服务时间敏感的物流服务定价策略,研究农村“货运班线”物流的时间与价格共同作用机制对“货运班线”效率影响,为农村物流运作模式提出一些理论参考与实践建议。
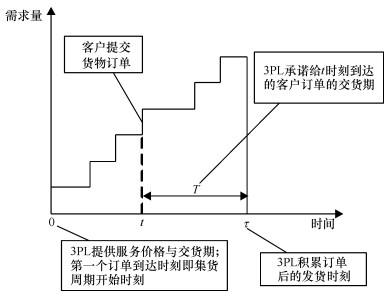
1 服务定价模型 1.1 模型假设本文研究的第三方物流企业主要从事农村零担与快递货运服务业务。该类企业服务采用“货运班线”物流服务模式,即依据固定班次时间及线路,让分布在农村的各类物流需求,通过定时定班次实现物流需求的集聚。因各类货物在时间上具有更多的不确定性,物流服务企业为了激励客户能及时将货物送到指定的收货点,采取物流服务价格与货物到达时刻相关的定价策略:企业确定一个固定时间周期让客户选择,客户到达时刻与班次时刻的时间差作为物流服务价格依据。因此企业决策中需要考虑的主要因素有:1)发货班次时间点(τ),该时间也是货物集中的最后截止时间,在此时间以前到达的货物都变成企业的物流需求,以后到达的货物变到下一个集货周期(如图 2);2)顾客到达时刻(t),该时刻影响到货物的交货期与物流服务价格,如果货物到达时间较早,利于第三方物流企业组织集货与配货,延长货物交货期,可以享受较低的服务价格;反之,如果货物到达时间较晚,增加第三方物流企业集货与配货难度,需要支付较高的物流费用。为了便于分析问题,有如下基本假设。
|
图 2 单个集货周期的物流活动示意图 Fig. 2 Logistics activity diagram of a single consolidation cycle |
假设1 每个客户货物订单重量与尺寸是标准的,即不考虑重量与尺寸对物流成本影响,该假设是为便于分析问题,若货物订单存在重量与尺寸的差异,可以分解成若干标准的订单。
假设2 订单到达率λ(p, T)=d-p-δT,是关于价格和交货期为的减函数,其中,d表达潜在客户需求;p表示物流服务价格;T表示企业承诺的交货期,此时交货期与客户订单到达时刻密切相关。设企业提供集货周期为τ,客户到达时刻为t,则订单的交货期T=τ-t。
假设3 假设物流服务价格函数为p=ρ-T,ρ表示物流单位订单的最高价格,根据假设2,得到物流服务价格与客户订单到达时刻的表达式为
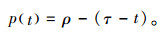
|
(1) |
假设4 假设物流服务中不考虑运输成本,考虑货物库存持有成本,设货物单位持有成本为h。
1.2 模型构建与求解根据假设2和3,得到客户订单到达率为

|
(2) |
根据客户订单到达率,物流企业集货周期τ内客户订单总需求为

|
(3) |
根据假设4,设在周期τ内到达的单位订单将会产生单位时间持有成本h,则物流服务企业在集货周期内的总利润为

|
(4) |
从上面利润公式可以看出,企业利润与货运班线的集货周期密切相关。在[p(t)-h(τ-t)]λ(t)>0条件下,企业利润是集货周期的增函数,集货周期越长,企业利润越高,难以判断企业决策内在规律,并且不同的集货周期产生利润不具备一定的可比性。因此采取企业利润与集货周期的比值,即单位周期内的企业利润率来评价企业决策效率,则利润率表示为

|
(5) |
为了简化分析,令K=d-ρ,ε=1-δ,其中,K>0,ε>0,客户到达率可以表示为
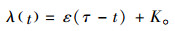
|
(6) |
因此在周期τ内的订单数量为
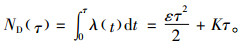
|
(7) |
总期望利润为

|
(8) |
可以得到利润率为

|
(9) |
其中,

|
从式(9)可以看出,利润率函数是一元二次表达式,在ad<0条件下,目标函数具有凹性。根据一阶条件,可得企业最优集货周期为

|
(10) |
因此企业最优利润率为

|
(11) |
同时,在周期τ内的订单总数为

|
(12) |
订单到达时刻的服务价格为

|
(13) |
命题1 时间敏感系数δ一定时,集货周期随单位持有成本增加而缩短;单位持有成本h一定时,集货周期随时间敏感系数的增加而缩短。
证明 对(10)求对单位持有成本的一阶偏导数得

|
同理,对公式(10)求对时间敏感系数的一阶偏导数得

|
综上所述,集货周期与单位持有成本、时间敏感系数呈负相关,命题1得证。
命题1表明,当单位持有成本增加时,物流企业将付出更多库存成本,为了节省成本,物流企业必须缩短集货周期。当时间敏感系数变大时,同样的等待时间下客户的效用会减少,导致客户订单数量减少,物流企业利润减少。
命题2 服务价格函数是一个关于时间t的一元一次函数族,该函数的最早时刻价格与单位持有成本、时间敏感系数均呈正相关。
证明 由式(13)可知,服务价格函数的最早时刻价格为

|
(14) |
对式(14)求对单位持有成本的一阶偏导数得

|
同理,式(14)求对时间敏感系数的一阶偏导数得

|
综上所述,该函数的纵截距与单位持有成本、订单到达率的时间敏感系数成正相关,命题2得证。
命题2表明,当持有成本增加时,物流企业只有提高订单价格才能获得更多利润。当时间敏感系数变大时,客户更加在乎订单交货期,物流企业适当的提高价格并不影响物流需求,可以获得更多利润。
命题3 当利润率与单位持有成本呈正相关时,与时间敏感系数呈正相关;反之,当利润率与单位持有成本呈负相关时,与时间敏感系数呈负相关。
证明:对式(11)求对单位持有成本的一阶偏导数得
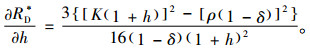
|
对式(11)求对时间敏感系数的一阶偏导数得

|
由于以上2个公式分子、分母均同号,故上面两个一阶偏导数符号相同,命题3得证。
命题3表明,利润率随单位持有成本、时间敏感系数这两个参数变化的方向一致,具体变化方向需依赖于其他参数值。
2 数值算例与敏感性分析为了进一步阐明本文配送模型的运作机制,假设货物单位持有成本h=2,潜在客户需求d=26,物流单位订单的最高价格ρ=25,时间敏感系数δ=0.1。配送模型中存在4个参数,其中潜在客户需求、物流单位订单的最高价格、时间敏感系数主要由市场决定,物流企业可以通过技术改革等缩减持有成本。本文主要探究持有成本、时间敏感系数这两个参数的独立变化对最优周期、服务价格、期望订单总数及利润率的影响,通过改变参数h、δ的取值,利用MATLAB软件编程计算得到一系列结果,如表 1所示。
| 表 1 参数h, δ的独立变化对相关结果的影响(d=26, ρ=25) Tab. 1 Influences of independent change of parameters h, δ on the related results |
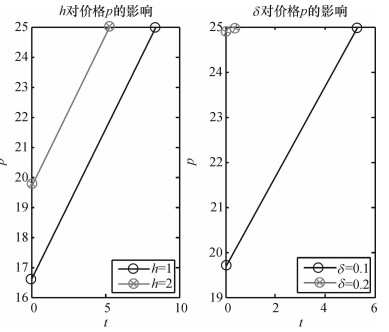
由表 1可知,集货周期分别随持有成本、时间敏感系数的增加而缩短,符合命题1;周期初始服务价格分别随持有成本、时间敏感系数的增加而增加,与命题2相符合;利润率分别随持有成本、时间敏感系数的增加而减少,与命题3相符。为了更直观分析最优周期、服务价格、期望订单总数及利润率随各参数的变化情形,作图 3~图 7,得到一系列结论。
|
图 3 h, δ对价格的影响 Fig. 3 Influences of h, δ on price |

|
图 4 h对最优周期、期望订单总数及利润率的影响 Fig. 4 Influences of h on consolidation cycle, expected total number of order and profit margin |

|
图 5 δ对最优周期、期望订单总数及利润率的影响 Fig. 5 δ on consolidation cycle, the expected total number of order and profit margin |

|
图 6 d对最优周期、期望订单总数及利润率的影响 Fig. 6 Influences of d on consolidation cycle, the expected total number of order and profit margin |

|
图 7 ρ对最优周期、期望订单总数及利润率的影响 Fig. 7 Influencesof ρ on consolidation cycle, the expected total number of order and profit margin |
1) 由图 3可知,在同一时刻,物流企业持有成本越高,服务价格越高;同样客户对时间敏感度越高,服务价格也越高。显而易见,持有成本越高,企业为了维持原有的盈利,必然会设置更高的服务价格;客户越关注订单到达时间,比如一般希望越早到达越好,越愿意出高价获得物流服务。因此,建议物流企业通过各种方法降低持有成本,同时根据客户对时间的敏感度,制定相应的服务价格,以获得更多盈利。
2) 由图 4可知,集货周期、期望订单总数及利润率均随持有成的增加而减少。显而易见,当持有成本越低时,物流企业利润率越高,建议企业通过各种方法降低持有成本;而在持有成本较低的情况下,建议物流企业延长集货周期以盈利更多;又由于在同一时刻的服务价格随集货周期延长而降低,农户受到低价的刺激,订单需求量随之增加。
3) 由图 5可知,集货周期、期望订单总数及利润率均随时间敏感系数的增加而减少。显而易见,客户对时间越不敏感,越不会因为集货周期而放弃物流企业的服务,订单到达数量也越多,同时,为了获得更多利润,建议物流企业延长集货周期。
4) 由图 6可知,集货周期随潜在客户需求的增加而缩短,利润率随之增加而增加。显而易见,当潜在客户需求很少时,为了达到一定订单数量,物流企业只能延长集货周期,此时企业仅能获得较低利润率;当潜在客户需求达到一定规模后,为避免供不应求的情况,企业将缩短集货周期,此时企业盈利增加。建议物流企业根据市场潜在需求设置集货周期,当潜在需求较少时,延长集货周期,反之缩短集货周期。
5) 由图 7可知,利润率是关于物流单位订单的最高价格的凹函数。当最高价格较低时,边际价格的增加大于边际需求量的减少,那么利润率随之增加;当最高价格继续增加时,边际价格的增加小于边际需求量的减少,此时利润率随之减少;当最高价格增加至某个水平后,物流企业将无利可图。
3 结论农村“货运班线”物流服务站点的定价集货策略直接影响到“货运班线”运营的效率,本文考虑客户到达时刻的物流服务定价决策问题,以期实现“货运班线”单位时间利润率最优。研究结果发现,集货周期随单位持有成本增加而缩短,集货周期随时间敏感系数的增加而缩短;最早时刻服务价格与单位持有成本、时间敏感系数均呈正相关,该结论对从事农村“货运班线”的物流企业决策提供一定的理论指导。本文仅仅考虑物流订单具有标准化(重量与尺寸相同)特征,在现实中不同的客户订单存在重量与尺寸的差异,因此考虑订单差异的物流服务定价是将来的研究方向。
| [1] |
王新利. 我国现行农村物流模式分析[J].
经济与管理研究, 2004, 25(3): 70-72, 80.
WANG Xinli. The current rural logistics mode analysis[J]. Economic and Management Research, 2004, 25(3): 70-72, 80. |
| [2] |
刘磊, 乔忠, 刘畅. 农超对接模式中的合作博弈问题研究[J].
管理工程学报, 2012, 26(4): 100-106.
LIU Lei, QIAO Zhong, LIU Chang. The study of the problem of cooperative game in farmes-supermarket model[J]. Journal of Industrial Engineering andEngineering Management, 2012, 26(4): 100-106. |
| [3] |
喻东. 浅析客运班车货物配送对农村物流配送的推动作用[J].
经营管理者, 2010, 26(16): 78.
YU Dong. Analyze the role of passenger train goods distribution to improve rural logistics distribution[J]. Manager Journal, 2010, 26(16): 78. |
| [4] |
白燕华, 张迎. 第三方物流企业传统定价机制综述[J].
中国证券期货, 2011, 19(4): 117.
BAI Yanhua, ZHANG Ying. Summary of third party logistics enterprisetraditional pricing mechanism[J]. China Securities Futures, 2011, 19(4): 117. |
| [5] |
李济球. 成本导向的第三方物流企业差别定价模型[J].
物流技术, 2015, 34(11): 189-191.
LI Jiqiu. Differential pricing model of cost-oriented third party logistics enterprise[J]. Logistics Technology, 2015, 34(11): 189-191. |
| [6] |
白燕华, 张迎. 第三方物流企业定价机制的供需博弈分析[J].
改革与开放, 2011, 26(8): 66-67.
BAI Yanhua, ZHANG Ying. supply and demandgameanalysisof third party logistics enterprisepricing mechanism[J]. Reform & Openning, 2011, 26(8): 66-67. |
| [7] |
谢天帅, 李军. 双垄断条件下第三方物流服务定价机制研究[J].
预测, 2007, 26(6): 48-52.
XIE Tianshuai, LI Jun. Study of third party logistics services pricing mechanism under dual monopoly conditions[J]. Prediction, 2007, 26(6): 48-52. |
| [8] |
谢天帅, 李军. 第三方物流服务定价博弈分析[J].
系统工程学报, 2008, 23(6): 751-758.
XIE Tianshuai, LI Jun. Gameanalysisof third party logistics enterpriseservicepricing[J]. Journal of Systems Engineering, 2008, 23(6): 751-758. |
| [9] |
谢天帅, 李军. 引入产品市场竞争时第三方物流服务定价研究[J].
工业技术经济, 2008, 27(3): 138-140.
XIE Tianshuai, LI Jun. Studyof third-party logistics service pricing when introducing product market competition[J]. Industrial Technology & Economy, 2008, 27(3): 138-140. |
| [10] |
孙小清, 李友林, 孙战旗. 基于Bertrand竞争的第三方物流企业定价分析及产业驱动策略[J].
物流技术, 2015, 34(13): 150-152.
SUN Xiaoqing, LI Youlin, SUN Zhanqi. Pricing analysis and industry driven strategy of third party logistics enterprise based on Bertrand competition[J]. Logistics Technology, 2015, 34(13): 150-152. |
| [11] |
杨文胜, 李莉. 响应时间不确定下的交货期相关定价研究[J].
中国管理科学, 2005, 13(2): 56-62.
YANG Wensheng, LI Li. Study of delivery time related pricing under uncertain response time[J]. Chinese Journal of Management Science, 2005, 13(2): 56-62. |
| [12] |
杨文胜, 徐滟, 李莉. 时间敏感需求下的交货期相关定价策略[J].
预测, 2005, 24(4): 70-73, 30.
YANG Wensheng, XU Yan, LI Li. Delivery time related pricing strategyunder time-sensitive demand[J]. Prediction, 2005, 24(4): 70-73, 30. |
| [13] |
林勇, 阎阅. 基于额外费用的交货期相关定价模型研究[J].
计算机集成制造系统, 2007, 13(5): 869-876.
LIN Yong, YAN Yue. Study of delivery time related pricing model based on additional cost[J]. Computer Integrated Manufacturing Systems, 2007, 13(5): 869-876. |
| [14] |
涂淑丽. 企业供应链交货期及相关定价决策分析[J].
统计与决策, 2011, 27(13): 71-73.
XU Shuli. Analysis of enterprise supply chain delivery time and related pricing decisions[J]. Statistics and Decision, 2011, 27(13): 71-73. |
| [15] |
申成霖, 卿志琼, 张新鑫. 零售商竞争环境下分散式供应链的定价与交货期联合决策模型[J].
中国管理科学, 2010, 18(3): 38-44.
SHEN Chenglin, QIN Zhiqiong, ZHANG Xinxin. A Joint decision model of decentralized supply chain pricing and delivery time underretailerscompetition[J]. Chinese Journal of Management Science, 2010, 18(3): 38-44. |
| [16] |
ULKU MA, BOOKBINDER JH. Optimal quoting of delivery time by a third party logistics provider: The impact of shipment consolidation and temporal pricing schemes[J].
European Journal of Operational Research, 2012, 36(1): 110-117.
|
 2016, Vol. 19
2016, Vol. 19
