欧美汽车租赁业的发展实践证明，收益管理是一种行之有效的管理方法。赫兹汽车租赁公司(Hertz)在1990~1991年间实施收益管理，使每辆车的平均收益由1%上升到5%^[1]。McGill和Van Ryzintl指出收益管理主要包括4个方面的内容：需求预测、超订、存量控制和动态定价^[2]。存量控制是企业进行收益管理的重要手段，是指为不同的价格水平分配合适的产品数量。存量问题研究主要分为静态和动态两种方法。最早提出静态模型的是Littlewood^[3]，建立了一个单航段随机二级价格模型，提出了边际座位收益原则。Belobaba^[4]、Brumells^[5]建立期望边际座位收益值(expected marginal seat revenue, EMSR)理论模型。随着研究的深入，研究者们开始考虑动态方法，将随时间变化的到达过程称为动态控制。Lee等^[6]建立了一个离散时间的动态规划模型。Subramanian等^[7]则考虑了顾客的退票和放弃预订行为，将座位的动态控制问题等价为一个经典的排队问题来加以解决。Feng等^[8]考虑了需求随时间变化的情况，并求出了动态舱位最优控制策略。

随着对收益管理研究的深入，学者已经开始考虑结合顾客选择行为，利用马尔可夫理论来辅助存量控制、需求预测及最终的收益优化。White^[9]对马尔可夫决策过程(Markov decision processes, MDP)在高速公路管理、航空订票系统等中的应用方面进行综述。Talluri等^[10]建立了基于顾客选择行为的存量控制的马尔可夫决策过程模型，证明在一定条件下可以获得最优嵌套控制策略。Khouja等^[11]假设租期是随机变量, 与顾客选择行为有关，设计运营策略使顾客尽早归还产品，加速产品周转率等。陈剑^[12]基于乘客选择行为，建立介于静态控制和动态控制之间的航空机票控制模型。梅虎^[13]以Logit模型为基础，针对顾客效用和偏好进行分析，建立了顾客舱位选择模型，从顾客的角度分析座位存量控制问题的必要性。李金林^[14]应用马尔可夫决策过程理论和稳健最优化方法建立存量控制的稳健模型，构建了一种稳健竞标价格策略。

现有的存量控制研究没有同时考虑到汽车租赁运营状态转移、顾客选择行为和车辆存量之间的相互影响。现实中，很多顾客因为租赁公司无车而被拒绝，但是在需求不旺时，往往又会出现车辆闲置的情况。本文将现实运营状态划分为可租赁状态和无法租赁状态，构建租赁状态转移状态空间，依据短时连续过程中运营状态分布的齐次性，将马尔可夫过程引入到研究中，通过时段划分采用短时模型叠加的方法，得到单位周期长时间连续运营状态转移的近似处理，构建连续短时段实时顾客行为变化检测策略，利用即时排队系统M/M/n/n/∞理论，对顾客的需求选择行为进行分析，确定存量最佳控制。

1 汽车租赁车辆的动态控制模型 1.1 动态规划与马尔可夫决策过程

动态规划是一种将复杂的多阶段或多周期问题转化成一系列比较简单的最优化问题的方法。多阶段或周期的问题分解成相互联系的若干阶段，不同阶段之间相互联系，本阶段的状态与决策仅仅影响下一个阶段的状态。当每个阶段的决策确定以后，整个过程的决策也就确定。

马尔可夫决策过程是马尔可夫链的扩展，其主要特征是允许概率和非确定性选择。马尔可夫决策过程的限界模型检测可以自由的对转移概率和极限概率进行检测，转移概率主要和某个时刻系统所处的状态有关，极限概率主要描述了长期运行中连续时间马尔可夫链处于某个状态的概率^[15-16]。

一个MDP有5个组成部分：

(1)

其中，S是系统所有可能的状态所组成的非空状态集，是非空有限的、可列的集合，也就是系统的状态空间。A(i)是在状态i∈S处可用的非空决策集，它可能与所处状态i有关。p_ij(a)是系统在决策时刻点n处于状态i，采取决策a∈A(i)使系统在下一个决策时刻点n+1时处于状态j的概率，它与起始决策时刻n无关。r(i, a)是系统在决策时刻点n处于状态i，采取决策a∈A(i)时系统在该阶段所获得的期望报酬。V是决策问题的目标函数或者准则函数。

1.2 汽车租赁系统的特性描述

每个顾客到达租赁系统是典型的随机过程，将汽车租赁过程用马尔可夫决策过程来描述。一般情况下，对租赁车辆的存量控制决策应依赖于过去的租赁价格、租车率等历史数据。但把决策规则限定在不依赖于历史数据而依赖当前状态的确定性马尔可夫决策规则内，其最优性结果与考虑所有决策规则是等价的，因此文中仅考虑确定性的马尔可夫决策，将决策规则限定在确定的马尔可夫决策规则中。利用短时模型叠加的方法得到单位周期长时间连续运营状态转移的近似处理，对系统状态进行概率实时解释，提供决策所依赖的当前状态。

在每个顾客到达租赁系统时，车辆租赁状态决定租赁系统接受顾客或者拒绝顾客。系统的状态空间集合为S={0, 1}，即无法租车和可以租车两种状态，其中0表示系统无法租赁车辆状态，1表示系统可以租赁车辆状态。系统运营状态从0到1的转移概率值为p₀₁；从1到0的转移概率值为p₁₀。由转移概率的性质可得状态转移概率矩阵P为

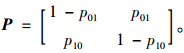
定义1  在状态空间集合S中系统状态转移后处于无法租赁状态的(后验)概率为δ∈[0, 1]，处于可以租赁状态的概率为δ^*∈[0, 1]，由全概率公式可求得：

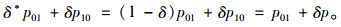
(2)

其中，p=1－p₀₁－p₁₀≥0。假设p₁₀≤1－p₀₁，即顾客需求越高租赁车辆越多，转移到无法租赁状态的概率越大，极限情况p₁₀=0时即租赁系统中车辆全部被租出去，租赁车辆供不应求。

定义2  系统运行n个周期时决策函数为f，所有策略为F_n。若系统处于状态i，则决策函数为f(i)，且f(i)∈A_N(i), i∈S，一个决策函数序列为策略π，则

π=(f₀, f₁, …, f_n), f_n∈F_n, n=0, 1，…, N。记算子▽δ=p₁₀+pπ可知：。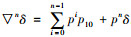

定义3  记折扣因子为β，在策略π的有限阶段的最优函数为：

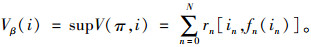
(3)

讨论系统的MDP模型，在系统平衡状态下，无法租赁状态(忙期)和可以租赁状态(闲期)均是随机变量，很难描述其准确的分布，因此需投入费用Q，利用短时模型叠加的方法近似对系统进行检测和记录。设C为系统在车辆全部被租赁的状态下运行一个周期的费用，R为增加存量更新系统所需的费用。

对n≥0，定义f⁽ⁿ⁾(δ)为系统在δ时运行n个周期，在最优策略运行的期望折扣费用，即

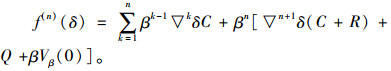
(4)

可以推算得下式：

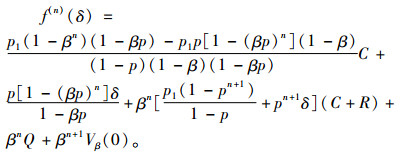
(5)

可以证明得^[17]：

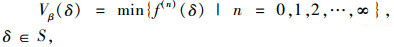
(6)

记n^*(δ)为上式取到n的最小值，即

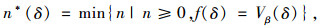
(7)

当δ=0即系统处于无法租赁状态时，由式(7)可知n^*(0)必须满足

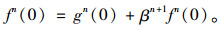
(8)

其中

(9)

由式(6)和式(8)可得

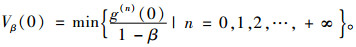
(10)

求解式(10)可得：当n^*(0)=+∞时

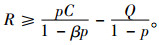
(11)

汽车租赁系统运行周期足够长时，系统需要更新的费用，即投放更多租赁车辆扩大经营规模的最小费用R等于其临界值。

1.3 稳健模型的建立

汽车租赁企业的租赁价格、租赁成本、租车率是决定租赁商收益水平的直接因素。待租汽车规模也是影响租赁商收入的重要因素，汽车租赁业不仅具有资金密集型的特点，同时具有规模效应。一辆租赁车辆的购置费用为A，运营费用包括车辆维护费用、保险费用、人员工资等其他费用。运营费用函数是关于运营时间T的二阶非负连续可微凹函数：ħ(T)=a₁+a₂T+a₃T²(a₁>0, a₂>0, a₃>0), 其中a₁为T=0时刻的汽车保险、维修等费用，a₂, a₃为汽车保险、维修等费用随时间递增系数。租赁车辆退出租赁系统时车辆残值，通常是依赖运营时间T的线性减函数：Β(T)=B－bT, 其中B为租赁商购得新车后立即卖出可得的利益(B < A)。由此可知，汽车租赁系统中每台租赁车辆运营成本关于运营时间T的函数为

(12)

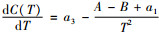
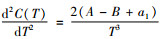
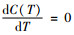
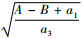
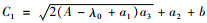
一阶导数为，二阶导数为。车辆的购置费用大于残值的最大值即A－B≥0，故运营成本函数C(T)是关于运行时间T的凸函数。当时可求得车辆最佳投入的最优使用时间为T^*= 。系统中每台租赁车辆单位周期最小运营成本为：。

设租赁商拥有Z种可选择租赁的车辆，顾客选择第z种车型的概率为q_z，设随机变量

，其中1表示第j个顾客选择第z类车型，0表示第j个顾客不选择第z类车型，z=1, 2, …, Z。显然ξ_jz服从两点分布：p{ξ_jz=1}= q_z，p{ξ_jz=0}=1－q_z。设单位时间内顾客到达系统的数量为D，租赁第j类车型的总数为，顾客选择租赁车辆是相互独立的，因此η_z服从二项分布，其期望E(η_z)=Dq_z，方差E(η_z)=Dq_z(1－q_z)。在可靠度为α的条件下，保证顾客租车需求满足率达到φ，即Φ(τ)=α，由De Moivre-Laplace中心极限定理可得到：

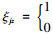
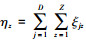
某类车型的控制存量数

，存量控制的车辆总数为。

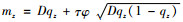
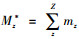
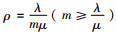
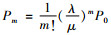
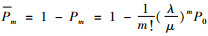
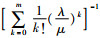
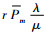
在汽车租赁服务系统中，到达的顾客数量和时间属于随机分布，同时车辆的使用时间完全取决于顾客需求，租赁车辆的时间也属于随机分布，因而汽车租赁服务系统是一个显著的随机排队服务系统^[18]。传统的排队系统中，单位时间内到达的顾客数服从参数为λ(λ>0)的泊松分布，顾客租赁车辆的租期服从参数为μ(μ>0)的负指数分布，租赁商拥有某类型m辆车，系统的总服务率mμ，系统的服务强度为。汽车完全租赁的概率为，顾客达到可租赁车辆的概率为：，其中P₀= 。在租赁系统周期t初始状态，租赁车辆确定的平均租金为r，租赁商拥有某类型m辆车单位周期的利润为Π(m)，系统运行单位周期的费用为C_m(C_m≥mC₁)。单位时间内顾客到达数和车辆租期是相互独立的，因此某类型m辆车单位周期的期望收入为，单位周期租赁每辆车缺货损失为U₁(U₁≥C₁)，期望缺货损失为P_mλU₁。传统的排队理论关注的重点是顾客的损失率，通常忽视系统中车辆定期的维修、保养以及例行的车辆检查，都使实际可租赁的车辆小于排队理论得到的可租赁车辆数，另外运营中由于顾客需求时间过于集中，高峰时段车辆的利用率过高，部分顾客需求无法满足，低峰时期大部分车辆闲置，造成其期望利润估计偏大。

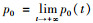
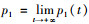
最优稳健策略目标是在系统顾客需求检测记录误差不可避免时，寻求使最差情况下的期望利润最大的最优策略^[19]。租赁商的最优稳健决策目标是最小的运营成本下期望利润取得最大值，即车辆租赁规模的扩大，忽略短期内顾客的租赁车辆需求变化，车辆出租率保持不变，近似考虑顾客租赁需求量等于单位周期达到的顾客数。汽车租赁系统进行策略检测过程中，记P₀(t)为系统t时刻无法租赁车辆的概率，全部车辆被租赁的概率，即租赁车辆的数量等于m的概率；p₁(t)为系统t时刻中可以租赁车辆的概率，即租赁车辆的数量小于m的概率。租赁车辆是一种易逝品，单位周期内未被租赁的车辆，租赁残值不存在。同时面对市场需求不确定性较大，通过对过多车辆存量导致的损失和过少存量导致的惩罚之间进行平衡^[18]，建立经典报童的策略利润期望函数：

(13)

最优动态车辆数m^*的求解算法如下。

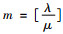
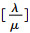
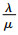
Step 1  统计分析单位周期日均顾客到达数和车辆租期，车辆初期配置数量，其中是不小于的最大整数。

Step 2  租赁系统中车辆数量为m时，检测记录可租赁状态和不可租赁状态的情况，建立概率转移矩阵，求解p₀₁, p₁₀, p₁, p₀。

Step 3  根据式(13)若策略利润期望Π_m < 0，则重新配置车辆数，否则转入Step 4。

Step 4  根据式(11)若车辆扩大经营规模的最小费用R≤C_m，则重复Step 2继续检测系统，否则转入Step 5。

Step 5  令m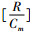^*= ，根据式(13)若m^*C₁≤ Π_m则输出租赁商最优存量控制租赁车辆数m^*，否则m^*=m^*－1转入Step 6。

Step 6  若m^*C₁>Π_m，m^*≤m则输出租赁商最优存量控制租赁车辆数m，否则输出租赁商最优存量控制租赁车辆数m^*。

2 算例分析

某汽车租赁公司开展车辆连锁租赁业务，其租赁站点主要设置在机场、城市中心商业区、旅游区、交通枢纽场站的附近，共有5种待租车型可供顾客选择：经济型轿车(EC)、商务型轿车(BC)、豪华型轿车(LC)、运动型多用途汽车(SUV)、7座及以上多用途汽车(MPV)。算例主要考察经济型轿车(EC)的存量控制。结合国内多家汽车租赁企业的实际数据，顾客到达的数量呈现周期性波动，在每周末及节假日达到高峰，这里以一周为动态控制的单位周期^[20-21]。

运营成本是影响利润的重要因素，通过对该租赁公司经济型轿车(均价10万元)实际运营成本的数据分析可以得到运营费用函数：

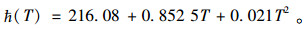
(14)

每台经济型轿车租赁车辆的运营成本的函数为

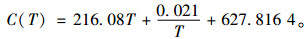
(15)

车辆最佳投入的最优使用时间为T^*=101周，车辆投入运营时间约为两年。汽车租赁系统中每台车辆单位周期最小运营成本为：C₁=630.9元。

该租赁商某个站点单位周期中日平均顾客达到数期望为125人，通过调查问卷获得顾客消费行为的偏好和效用，运用变精度粗糙集方法对影响顾客选择行为的因素进行简约并构造判断矩阵计算权重，用Logit模型描述顾客选择行为，假设顾客选择概率与购买时间无关，计算出顾客选择租赁经济型轿车概率p{ξ_jz=1}=q_z=0.334^[22]。租赁商采用时租与日租相结合的策略，租期参数μ=0.938，日租金收益平均为175元。单位周期内该租赁商实际经济型轿车存量准备的车辆数m=45辆。

在实际租赁流程中，租赁商在晚上22:00到次日早上8:00在各个站点之间进行车辆调度，顾客进入汽车租赁系统中均认为可租赁到车辆，系统状态保持在可租赁状态，早上8:00到晚上22:00顾客可以到租赁站点租赁或归还车辆，车辆归还后经过保养维护进入租赁系统的时间前，租赁系统的保持当前状态，因此租赁业务流程时间可认为系统在特定态下稳定平均持续时间。策略检测时间以30 min进行时段划分，可以得到单位时间系统运行数据，如下表 1。

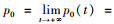
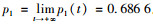
利用Matlab软件对数据进行处理，转移概率可用频率近似表示。系统从无法租赁状态转移到可以租赁状态的转移概率值为P₀₁≈0.333 3；系统从可以租赁状态转移到无法租赁状态的转移概率值为P₁₀≈0.152 2。由极限概率分布的性质可知，系统t时刻无法租赁车辆的概率, 全部车辆被租赁的概率，租赁车辆的数量等于m的概率0.313 4；系统t时刻中可以租赁车辆的概率，即租赁车辆的数量小于m的概率。

单位周期策略利润期望：Π^*(m)=7 323.1元。租赁系统运行状态的检测以及数据的记录费用Q可以近似忽略，单位时间费用现值折扣率不变，假设β=1，投放更多租赁车辆扩大经营规模满足顾客需要的最小费用：

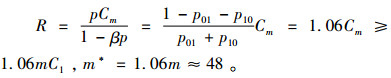
(16)

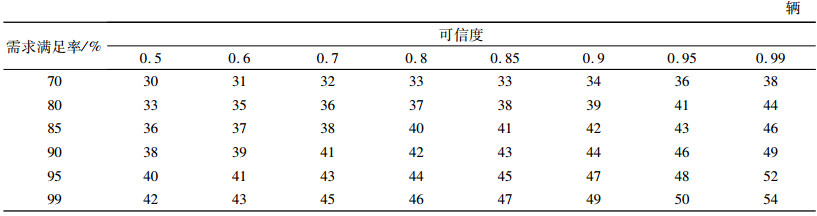
增加车辆运行费用小于当前单位周期策略利润期望即Π^*(m)>(m^*－m)C₁=1 892.7元，满足条件，此时系统经济型轿车应投放48辆，在可信度为0.95的条件下满足95%的顾客需求可以租赁车辆。可以得到不同可信度条件下，满足不同比例顾客选择经济型轿车需求的建议存量控制数，如下表 2。

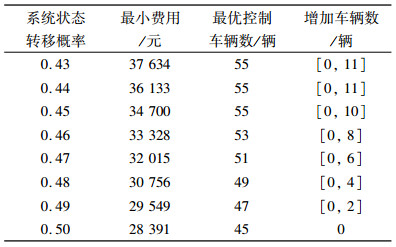
系统运行多个周期后处于可租赁状态和不可租赁状态之间进行转移的频率近似认为是转移概率，存在的几种特征状态情况及相应的最优控制车辆数，如下表 3。

由上表得到，系统在可租赁状态和无法租赁状态之间转移次数越多，说明车辆周转率越高，更能够满足顾客的需求。租赁系统中顾客归还车辆的时间间隔越小，系统从无法租赁状态向可租赁状态转移概率越大；顾客到达达到租赁系统中时间间隔越大，系统从无法租赁状态向可租赁状态转移概率越大。

3 结论

在动态市场条件下，有效的汽车租赁系统会持续地检测评估顾客需求、租期、存量等相关的变化要素，以适应市场的变化。随着微观顾客市场的发展变化，收益管理的策略以及战术都会随之调整。本文综合考虑顾客的到达和选择行为，着重研究单位周期长时间连续运营状态转移情形下的最优存量控制决策，较以往有关汽车租赁收益管理的研究，在以下几方面进行了改进：1)顾客到达的时间、需求量、顾客选择车型以及租期都是随机不确定的，完全取决于顾客和租赁系统运行状态，这与现实情况相符；2)充分考虑了顾客对租赁车辆的选择行为，并采用选择概率的方式来刻画需求；3)对单位周期长时间连续运营状态转移情形进行持续地检测评估，能够减小即时排队理论中，因车辆维修养护等原因造成的实际投入车辆与理论车辆数之间的存在差值。

顾客选择行为会因年龄、性别等自身因素和租赁商销售策略、租赁价格等外界因素的影响而改变，所以捕捉顾客选择概率随时间变化的规律，进而探讨其对租赁商库存策略和具体决策的影响是值得研究的内容。