六西格玛管理近年来在企业质量管理领域得到了广泛的推广和应用,通过六西格玛质量改进活动,能够大幅度降低生产过程中产品不合格品率和产品缺陷率,使得过程绩效达到每百万件产品中仅有3.4件不合格产品或缺陷,即每百万个机会缺陷数(DPMO, defects per million opportunities)为3.4[1]。在六西格玛管理的DMAIC(define-measure-analyze-improve-control)方法中,统计过程控制技术在监测和改进过程质量中发挥着巨大的作用,但随着企业质量水平达到或接近六西格玛时,传统的统计质量控制方法将无法适用于这种接近零缺点的高质量过程(High-yield processes)。对于高质量过程,由于其不合格率或缺陷率很低,使用传统的计数值控制图来进行监控,经常会出现经过很长一段时间才能监测到一个不合格品或缺陷点,即控制图上会出现很多统计量为零的点,容易让使用者误以为生产过程状态良好[2]。为了提高对高质量过程的监控能力,人们提出了累积计点值控制(cumulative quantity control, CQC)图[3]和累积计件值控制(cumulative counts control, CCC)图[4]来作为传统的c控制图和p控制图的替代方法。有关如何深化和加强CCC图的应用,可以参考Lai等[5]、TANG等[6-7]、马义中等[8]、宋宗伟等[9]的研究成果。本研究主要针对CQC图进行研究,对于传统的控制图方法,可以通过增加报警准则的方法来提高常规控制图的监控效率[10],为了提高CQC图的监控效率,本文将研究对控制图的报警准则进行调整,即在原有的出界报警准则的基础上,分别讨论几种不同的报警准则,如连续两点出界、连续三点中有两点出界、连续三点出界等情况下CQC图的设计方法。通过平均运行长度(average run length, ARL)作为监控效率评价指标的计算和比较分析,说明这种多点报警的CQC控制图设计方法的有效性。
1 CQC控制图CQC图最早由Chan等[3]提出,不同于c控制图以缺陷发生的数目为监控对象,CQC图以2个缺陷之间的累计检验的产品数Q作为监控对象来构造统计量。Q服从参数为λ0的指数分布,其概率密度函数和累积分布函数分别为
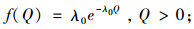
|
(1) |
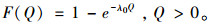
|
(2) |
其中, λ0为平均缺陷率。
设控制图虚发报警的概率为α,则由指数分布可知,双边CQC图的上下控制界限为

|
(3) |
在CQC图中,若有点低于下控制限LCL,则表示2个缺陷之间的累计检验的产品数下降,即缺陷率上升,说明该过程质量下降;而当有点高于上控制限UCL,则表示两个缺陷之间的累计检验的产品数增加,即缺陷率下降,说明该过程质量进一步提高了。当CQC图的监控目的着重于监控质量下降的情形时,上述双边的CQC图可以简化为只有下控制限的单边CQC图。
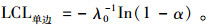
|
(4) |
在以上的控制图中,如果出现一个点超出控制界限,则认为过程出现异常,发出报警。但是如果将报警准则改变成连续两点出界、连续三点中有两点出界、连续三点出界等几种情况,为了保持相同的虚发报警的概率,就需要对控制界限进行相应的调整。这样,调整了报警准则和控制界限后的就可以获得几种新的CQC控制图方法。由于虚发错误报警的概率的倒数等于受控情况下的平均运行长度ARL0,我们可以通过ARL0获得这几种CQC控制图的控制界限,于是下面我们来讨论报警准则改变后的CQC控制图的平均运行长度。
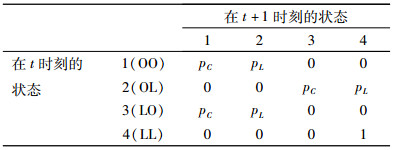
2 平均运行长度的计算单边CQC图的平均运行长度可以采用马尔可夫转移矩阵的方法进行计算。首先,将该控制图划分为2个区域,即下控制限以上和下控制限以下。分别用pC和pL来表示控制图上有一个点落在这2个区域的概率,其中pC+pL=1。例如,对于以报警准则为连续两点出界的单边CQC图,如果把CQC控制图的作图过程看作是一个马尔可夫链,则在某一个时刻该控制图可能分别处于以下4种状态,状态1(OO):连续的2个点都处于下控制限之上;状态2(OL):连续的2个点中,第1个点处于下控制线之上,第2个点在下控制限之下,即第2个点出界;状态3(LO):连续的2个点中,第1个点在下控制限之下,第2个点处于下控制线之上,即第一个点出界;状态4(LL):连续的2个点都在下控制限之下,即2点都出界。前3个状态都代表着该生产过程仍处于受控状态,而状态4则表示过程处于失控状态,且状态4是一个吸收点,即过程一旦失控,则转变为其他受控状态的概率为0。由此可得该马尔可夫链的转移概率矩阵。
| 表 1 马尔可夫链的转移概率矩阵 Tab. 1 Transition Matrix of Markov Chain |
平均运行长度(ARL)可以用从初始的状态1转移到表示失控的状态4所需要转移的步数的数学期望来表示。解下述方程组:
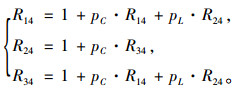
|
(5) |
Ri4表示从状态i转移到状态4所需要的步数的数学期望,而R14即为ARL。由pC+pL=1,报警准则为连续两点出界的单边CQC图的平均运行长度可以表示为
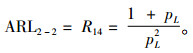
|
(6) |
同理,其他2种改变报警准则控制图的平均运行长度分别可以表示为
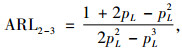
|
(7) |
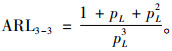
|
(8) |
可以把这一类将报警准则分别改变成连续两点出界、连续三点中有两点出界、连续三点出界的控制图记为CQC2-2、CQC2-3和CQC3-3。设虚发报警的概率∂=0.002 7,则受控状态下的平均运行长度ARL0=1/∂≈370。由式(6)、(7)、(8)可得,在受控的CQC2-2、CQC2-3和CQC3-3图中一个点超出下控制线的概率pL为pL2-2=0.053,pL2-3=0.038,pL3-3=0.147。以pL代替式(4)中的α,即可求得CQC2-2、CQC2-3和CQC3-3的下控制限:LCL单边=-λ0-1In(1-pL)。
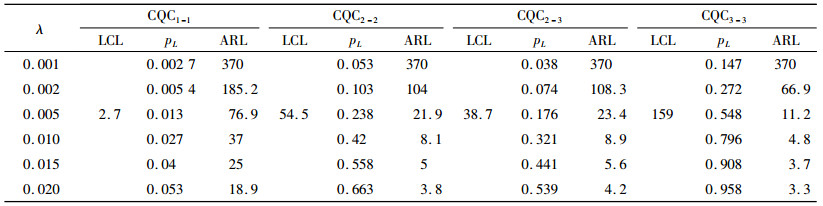
3 效率比较分析在控制图的判别规则和控制线确定后,就可以进行缺陷率的日常监控。当过程中存在异常因素的干扰时,缺陷率由λ0变化为λ,同时pC和pL也会随之而改变,可以通过式(4)、(5)、(6)计算失控平均运行长度,分析控制图的监控效率。表 2~4分别是在虚发报警的概率为α=0.002 7,缺陷率λ0为0.0010、0.000 5、0.000 1的情况下,当缺陷率出现不同程度增大时,采用各种报警准则的单边CQC图的平均运行长度。
| 表 2 采用各种多点报警准则的单边CQC图的平均运行长度(λ0为0.001) Tab. 2 ARL of CQC charts with one side control limit under different alarm rules (λ0=0.001) |
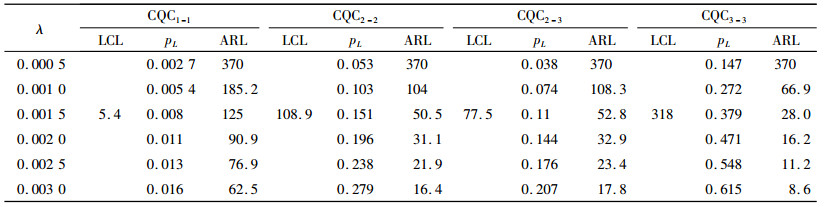
| 表 3 采用各种多点报警准则的单边CQC图的平均运行长度(λ0为0.000 5) Tab. 3 ARL of CQC charts with one side control limit under different alarm rules(λ0= 0.000 5) |
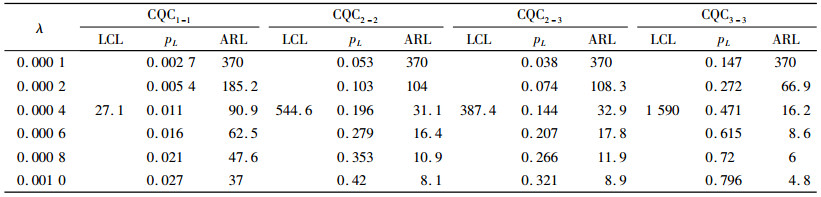
| 表 4 采用各种多点报警准则的单边CQC图的平均运行长度(λ0为0.000 1) Tab. 4 ARL of CQC charts with one side control limit under different alarm rules(λ0= 0.000 1) |
从表 2~4中可以发现,CQC2-2、CQC2-3和CQC3-3在缺陷率上升后的平均运行长度都要显著小于CQC1-1,其中尤以CQC3-3的监控效率最高,其次是CQC2-2,最后是CQC2-3。由此可以说明采用多点报警的累积计点值CQC控制图是一种简单高效的高质量过程监控方法。
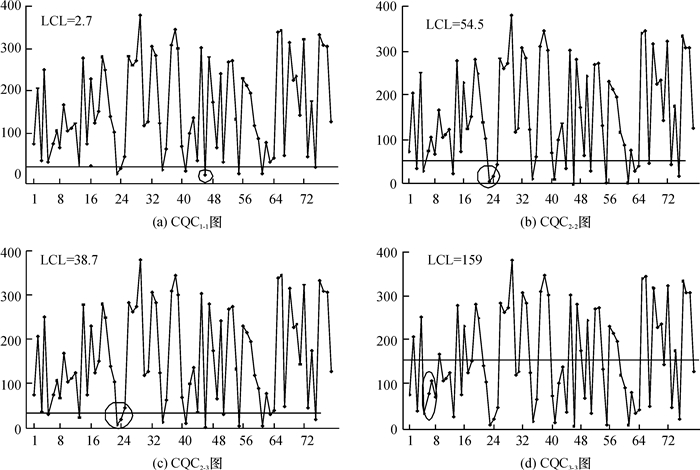
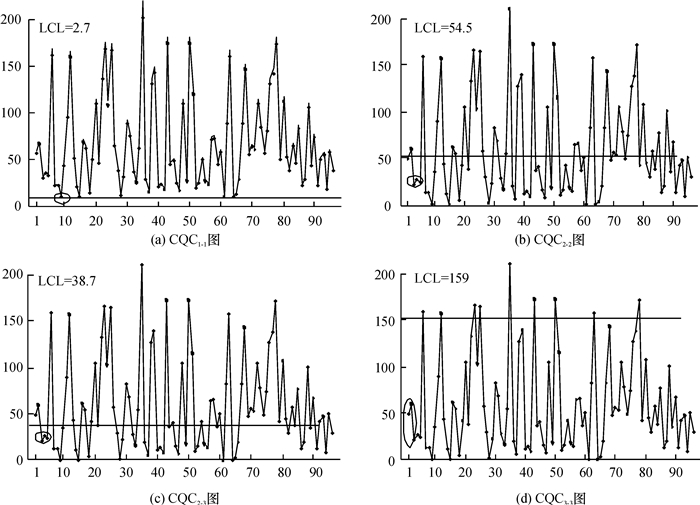
4 仿真算例为了进一步验证上述对各类CQC图的监控效率对比分析的结论,本文采用MATLAB计算机仿真来说明采用多点报警的累积计点值CQC控制图的使用。设某高质量生产过程在稳定状态下的缺陷率λ0为0.001,要求稳定状态下虚发报警的概率不大于α=0.002 7,这时由表 2可知,分别构造的以2个缺陷之间的累计检验的产品数Q作为监控对象的各类CQC图为LCL1-1=2.7;LCL2-2=54.5;LCL2-3=38.7;LCL3-3=159。图 1和2分别为采用这4种CQC图对缺陷率由0.001变化为0.005和0.015时的仿真数据进行监控的结果。从图中可以发现,CQC3-3图上出现异常报警的速度最快,在图 1(d)和图 2(d)中分别在第7点和第3点报警;CQC2-2和CQC2-3图出现异常报警的速度相近,CQC2-2在图 1(b)和图 2(b)中分别在第24点和第4点报警;CQC2-3图在图 1(c)和图 2(c)中分别在第24点和第4点报警;CQC1-1图的报警速度最慢,在图 1(a)和图 2(a)中分别在第46点和第10点报警。
|
图 1 当缺陷率λ=0.005时的多点报警CQC控制图(λ0为0.001) Fig. 1 CQC charts under different alarm rules for λ=0.005 (λ0= 0.001) |
|
图 2 当缺陷率λ=0.015时的多点报警CQC控制图(λ0为0.001) Fig. 2 CQC charts under different alarm rules for λ=0.015 (λ0=0.001) |
本文提出了一种基于多点报警的CQC控制图方法,它以ARL作为性能度量,以已知的虚发报警的概率和稳定状态的缺陷率为先决条件,根据报警规则的变化计算相应的控制下限,以判断高质量生产过程是否发生缺陷率上升的异常变化。这种方法是对一般的CQC方法的一种改进,通过上面的比较可以说明它能更灵敏地对高质量过程中出现的较小波动进行监测,也更符合实际生产加工过程中尽量减少质量损失的要求。
| [1] |
马林, 何桢.六西格玛管理[M].北京:中国人民大学出版社, 2007.
|
| [2] |
GOH T N, XIE M. Statistical control of a six sigma process[J].
Quality Engineering, 2003, 15(4): 587-592.
DOI: 10.1081/QEN-120018391. |
| [3] |
CHAN L Y, XIE M, GOH T N. Cumulative quantity control charts for monitoring production processes[J].
International Journal of Production Research, 2000, 38(2): 397-408.
DOI: 10.1080/002075400189482. |
| [4] |
GOH T N. A control chart for very high yield processes[J].
Quality Assurance, 1987, 13(1): 18-22.
|
| [5] |
LAI C D, XIE M, GOVINDARAJU K. Study of a markov model of a high-quality dependent process[J].
Journal of Applied Statistics, 2000, 27(4): 461-473.
DOI: 10.1080/02664760050003641. |
| [6] |
TANG L C, CHEONG W T. CCC chart with sequentially estimated parameter[J].
ⅡE Transactions, 2004, 36(9): 841-853.
|
| [7] |
TANG L C, CHEONG W T. A control scheme for high-yield correlated production under group inspection[J].
Journal of Quality Technology, 2006, 38(1): 45-54.
DOI: 10.1080/00224065.2006.11918583. |
| [8] |
马义中, 刘阳. 高质量过程控制技术的比较研究与分析[J].
数理统计与管理, 2008, 27(3): 473-479.
MA Yizhong, LIU Yang. Comparison and analysis of high quality processes monitoring technologies[J]. Application of Statistics and Management, 2008, 27(3): 473-479. |
| [9] |
宋宗伟, 宋向东. 高产过程的CCC-r图控制限优化[J].
辽宁工程技术大学学报, 2014, 33(4): 535-538.
SONG Zongwei, SONG Xiangdong. Optimization of CCC-r chart limits of high yield processes[J]. Journal of Liaoning Technology University, 2014, 33(4): 535-538. |
| [10] |
王海宇, 徐济超. 基于多点报警多元统计过程控制[J].
数理统计与管理, 2006, 25(6): 709-715.
WANG Haiyu, XU Jichao. Multivariate statistical process control based on multiple dotes alarm rules[J]. Application of Statistics and Management, 2006, 25(6): 709-715. |
 2016, Vol. 19
2016, Vol. 19