2. 同济大学 经济与管理学院,上海 200092
2. School of Economics and Management, Tongji University, Shanghai 200092, China
在传统的库存控制模型中,决策目标是最小化系统的平均成本,往往忽略产品的销售价格,即使考虑,一般也被看作外生变量。然而,在经济实践中商家常常通过创新的定价策略来对库存进行有效地管理,如广泛用于航空、酒店、租赁等领域的收益管理技术[1]。Gallego等[2]指出在零售行业中定价技术对提升利润也有着非常重要的作用。自Whitin[3]首次在库存控制模型中考虑定价决策后,库存控制与定价联合决策问题吸引了许多学者的注意。
易变质品是库存物品的一个重要组成部分,由于其易于变质的特性更有必要通过定价策略对其需求进行管理。比如对于果蔬类农产品,随着产品新鲜度的下降其需求也会降低,此时商家会通过降价促销的手段来吸引一些顾客,从而将产品销售出去。另外,对于一些服装类的快销时尚品牌,在销售季节开始时基本需求较为旺盛,销售价格也会相对较高;随着时间的推移,产品价值逐渐下降,因此基本需求也会相应减少;此时如果库存量仍然较大,商家会采取降价的方式进行促销,以减少库存积压、降低损失。Cohen[4]较早讨论了易变质品的联合订购和定价问题,假设需求与销售价格相关、变质率为常数,同时考虑了完全损失和完全延迟订购两种情况。Abad[5]假设需求是关于销售价格的任意减函数,变质率是关于时间的函数,部分延迟订购率与等待时间相关,构建了一个易变质品的联合订购与定价问题。然而,在其模型中没有考虑缺货情况下的成本(包括延迟订购成本和损失销售成本)。针对这一不足,Dye[6]在利润函数中同时考虑了延迟订购成本和损失销售成本,构建了一个部分延迟订购率为倒数形式的易变质品联合定价-订购模型。后来,Dye等[7]在考虑指数形式的部分延迟订购率的基础上构建了一个类似的模型。Sana[8]构建了一个更为一般的定价与订购模型,假设部分延迟订购率是关于等待时间的任意连续可微函数。
以上模型均假设需求只依赖于产品的销售价格。事实上,对于果蔬类和时尚类等易变质品来说,较高的库存水平对增加销售具有积极的影响,即需求依赖于库存水平。很多库存模型中都考虑了需求依赖于库存水平的情况,Urban[9]给出了国外此类问题的一个相关研究综述。国内这方面的研究也有很多。罗兵等[10]在需求同时依赖于时间和库存水平、常数变质率、时变购买成本、允许缺货且缺货量完全延迟的假设基础上,构建了一个有限时域内等周期且各周期服务水平相同的易变质品库存模型。罗兵等[11]进一步考虑时变短缺量拖后率以及资金时间价值等因素对易变质品库存管理的影响,建立了相应的EOQ模型。徐贤浩和李锐娟[12]假设需求受库存水平影响,无形变质率与需求率负相关,建立了短生命周期物品的库存模型。闵杰和周永务[13]针对非立即变质品,考虑了一个需求依赖于库存水平,变质率为常数且部分延迟订购的最优库存控制问题。段永瑞等[14]讨论了一个需求依赖于库存水平,变质服从两参数Weibull分布,缺货量部分延迟订购且延迟订购率与等待时间相关的库存控制问题。
以上关于易变质品的库存控制研究中,假设需求或者受价格的影响,或者受库存水平的影响。而实践中,易变质品的需求会同时受到多种因素的影响。Teng等[15]针对易变质品,构建了一个生产率和变质率均为常数的联合定价和生产模型,假设产品的需求同时依赖于库存水平和价格,系统不允许缺货。Hou等[16]考虑通货膨胀和货币的时间价值,假设产品的变质率为常数,需求同时受库存水平和价格的影响,缺货量完全延迟订购,构建了一个有限时域内的库存模型。文献[17-18]讨论了需求同时依赖于价格和库存水平,变质率为常数,允许零售商延迟支付货款,不允许缺货且期末库存水平不为零的非立即变质品的库存系统的最优补货问题。Shah等[19]在考虑通货膨胀和货币的时间价值基础上讨论了对易变质品库存系统进行最优订购、定价和保鲜技术投资决策的问题,其中需求同时依赖于价格和库存水平,变质率为常数,系统同时进行保鲜技术投资以降低产品的变质率,不允许缺货且系统存在残次品。
然而,在以上考虑需求同时依赖于销售价格和库存水平的模型中多假设产品的变质率为常数,且系统不允许缺货或完全延迟订购。针对以上不足,本文考虑一个需求同时依赖于销售价格和库存水平,产品的变质率随时间发生变化,系统缺货量部分延迟订购且部分延迟订购率是关于等待时间的减函数的订购与定价联合决策问题。此外,本文在目标函数中考虑已变质产品的处理成本,而以上文献中大多未考虑这一成本要素。实践中对已变质产品的处理成本是存在的并且会对库存和定价策略产生影响。当变质处理成本较大时,订购量或生产量会减少,定价策略也会发生变化。在以上假设基础上本文构建相应的订购与定价联合决策模型,进而证明模型解的存在性,并提出相应的数值求解算法。最后通过算例,展示了模型和算法的应用,并对主要参数的灵敏度进行了分析。
1 假设和符号表示文中用到的假设和相关符号表示。
1) 计划时域无限且系统的订货提前期为零。
2) I(t)表示t∈0, t1+t2时刻的库存水平。其中,t1(t1≥0)表示在补货周期内库存水平为非负的时间段长度(决策变量);t2(t2)≥0表示库存水平为负(或缺货)的时间段长度(决策变量);T=t1+t2为总的补货周期的长度;I0表示期初库存水平,即I0=I(0);S表示最大缺货量,即S=-I(T)。
3) 变质率θ(t)是关于时间的任意非负有界可微函数,且0≤θ(t)≤1。
4) A表示固定订购成本;Cp表示单位购买成本;p表示单位销售价格,且p>Cp (决策变量);Ch表示单位产品单位时间的库存持有成本;Cd表示单位变质产品的处理成本;Cs表示单位产品单位时间的缺货成本;Co表示在缺货期内由于损失单位销售而引起的机会成本;Q表示一个补货周期内的订购量;TP表示一个补货周期内库存系统的总利润;AP表示单位时间的平均利润。
5) 当库存水平非负时,需求同时依赖于销售价格和库存水平,表示为D=α(p)+βI(t), t∈[0, t1],其中,α(p)≥0和0≤β<1;当库存水平为负时,即仓库里或货架上没有库存,需求率仅与销售价格相关,表示为D=α(p), t∈[t1, t1+t2]。此外,α(p)是关于p的严格减函数,即dα(p)/dp<0,且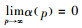
6) 系统缺货时,缺货量部分延迟订购,且部分延迟订购比例B(τ)是关于等待时间τ的任意减函数[5]。此外,0≤B(τ)≤1,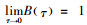
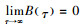
基于假设5)和6),该库存系统的实际需求率可表示为
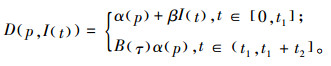
|
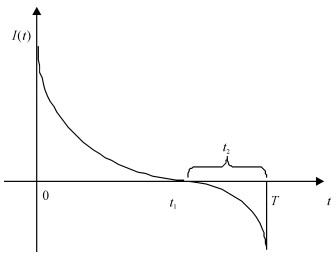
由假设可知,在时间段[0, t1]内,库存水平在需求和变质的共同作用下逐渐下降,到t=t1时刻下降到0,即I(t1)=0,此时缺货开始发生;在时间段(t1, T]内,库存水平在需求的作用下继续下降。图 1是一个补货周期内库存水平随时间的变化示意图。
|
图 1 补货周期内库存水平随时间的变化示意图 Fig. 1 Inventory level pattern in a replenishment cycle |
在t∈[0, t1]时刻,I(t)满足
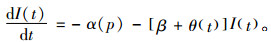
|
(1) |
已知边界条件I(t1)=0,求解式(1)得
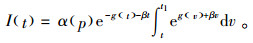
|
(2) |
其中, 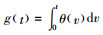
在缺货期(t1, t1+t2]内,对延迟的需求采用“先到先服务”的原则,那么可知顾客的在t时刻的等待时间为τ=t1+t2-t。因为库存水平为负,所以不存在变质问题。因此,在t∈(t1, t1+t2]时刻,I(t)满足
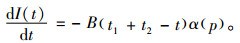
|
(3) |
已知边界条件I(t1)=0,求解式(3)得
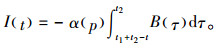
|
(4) |
综上可知,整个补货周期的订购量为
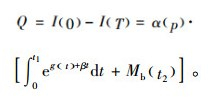
|
(5) |
其中, 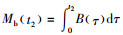
那么,一个周期内的利润构成要素如下。
1) 固定订购成本:FC=A。
2) 购买成本:
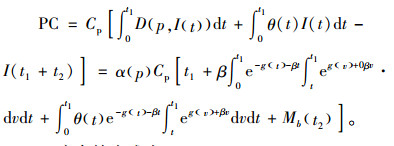
|
3) 库存持有成本:
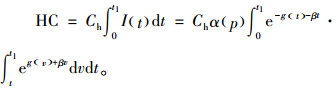
|
4) 变质处理成本:
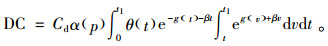
|
5) 缺货成本:
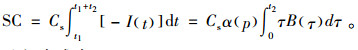
|
6) 机会成本:
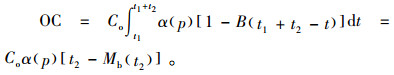
|
7) 销售收入:
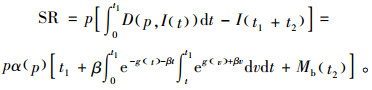
|
因此,一个补货周期内的总利润为
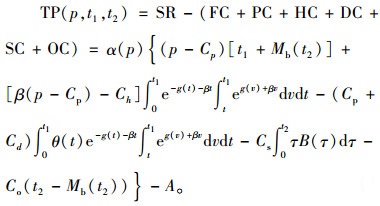
|
(6) |
从而,单位时间的平均利润为
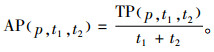
|
(7) |
目的是求解最优的p、t1和t2,使AP(p, t1, t2)最大化,其必要条件是同时求解式(8)~(10)。
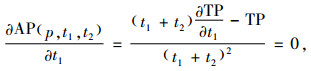
|
(8) |
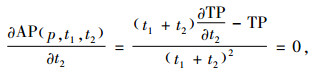
|
(9) |
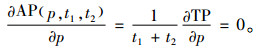
|
(10) |
其中,
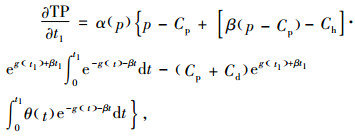
|
(11) |
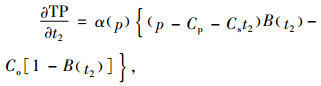
|
(12) |
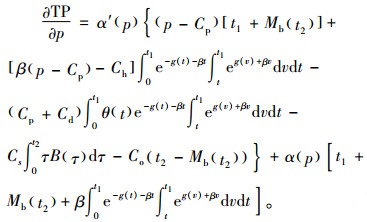
|
(13) |
说明1 如果p<Cp+Cst2成立,由式(12)可知有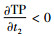
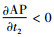
定理1 对于任意给定的p,如果β(p-Cp)-Ch≤0,那么最优补货策略(t1*, t2*)可通过求解式(8)和式(9)唯一确定。
证明 由式(11)和式(12),有
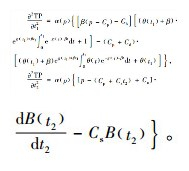
|
容易知道,当β(p-Cp)-Ch≤0时,有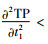
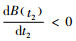
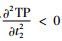
由式(8)和式(9)易得
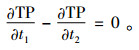
|
(14) |
令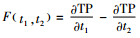
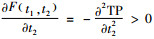
由p≥Cp+Cst2,可知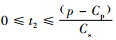
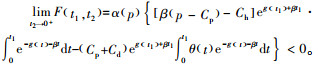
由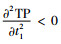
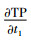
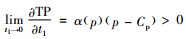
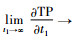
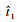
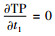
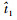
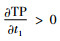
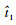
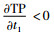
可知当t1≤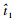
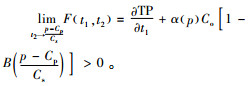
因此,对任意给定的t1∈(0, 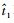
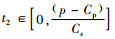
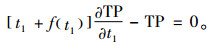
|
(15) |
令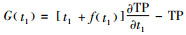
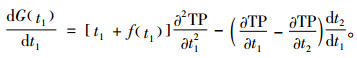
|
(16) |
将式(14)代入式(16),得
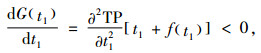
|
即G(t1)关于t1严格递减。此外,由式(14)可得到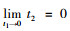
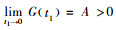
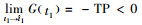
接下来验证(t1*, t2*)为最优解的二阶充分条件。容易得到
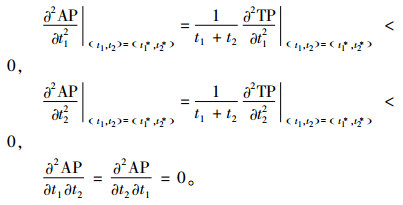
|
令H为AP(p, t1, t2)的海塞矩阵,有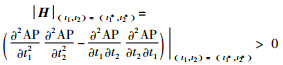
说明2 1)从管理角度来看,β(p-Cp)表示由持有单位库存而获取的收益,而Ch是单位库存的持有成本。那么β(p-Cp)-Ch≤0意味着持有单位库存带来的收益要小于成本,因此允许缺货策略对系统将是有益的,即β(p-Cp)-Ch≤0是本文所构建模型成立的先决条件。2)当p预先给定时,此时的目的是寻找最优补货策略。如Abad[5]所述,这类问题在一些情况下是适用的,比如销售者处于高竞争市场上,不能随意更改市场规定的价格;或供销合同中已规定了商品的价格的情况。此外,这类问题对于销售和运营部门单独进行决策的企业来说也是普遍存在的。销售部门首先根据市场情况决定产品的销售价格,运营部门再基于这一价格做进一步的生产或订购决策。
定理2 对于给定的补货策略(t1, t2),如果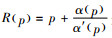
证明:1)通过一定的代数变换,可知式(10)等价于
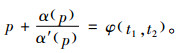
|
(17) |
其中,
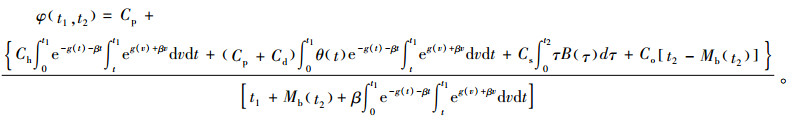
|
由α(p)≥0,α′(p)<0和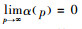
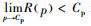
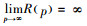
接下来验证p*为最大值点的二阶充分条件。容易得到:
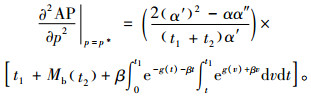
|
(18) |
因R(p)关于p严格递增,故(α′)2-αα″>0,从而2(α′)2-αα″>0。又有t1, t2≥0,α′<0和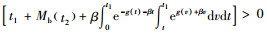
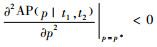
2) 显然,如果R(p)关于p并不是严格递增,那么式(17)可能存在多个局部最优解,而最优解可通过穷举搜索AP(p, t1, t2)的方法得到。证毕。
说明3 文献中常见的与价格相关的需求函数α(p)=m-np和α(p)=mp-n (m, n>0)均满足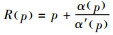
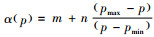
推论1 如果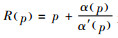
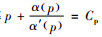
证明 单独定价决策模型即不考虑运营成本时系统的平均利润函数可表示为
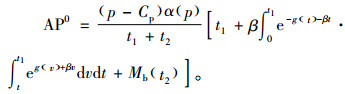
|
此时的最优销售价格p0存在的一阶必要条件为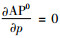
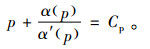
|
(19) |
由式(17)显然有φ(t1, t2)>Cp。因此,如果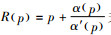
|
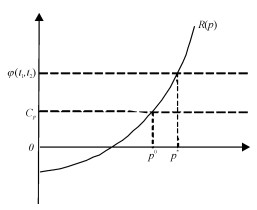
图 2 p*和p0的关系图 Fig. 2 The relationship between p* and p0 |
说明4 推论1指出订购与定价联合决策下得到的最优销售价格高于单独进行定价决策时得到的最优销售价格。因此,对于一个企业来说,销售部门不考虑运作部门的成本而决策的销售价格将会偏低。如果运作部门采用这一价格来预测需求并决策订购/生产策略,那么得到的策略对整个系统来说并不是最优的。
3 算法基于定理1和定理2,在这一部分将给出一个算法用于搜索模型的最优解。
第1步:从k=1开始,给出一个合适的值p(k)∈(0, ∞)作为p的初值,即p=p(k)。
第2步:对于给定的p=p(k),求解式(8)和式(9)构成的方程组,并将结果标记为(t1(k), t2(k))。
第3步:将(t1, t2)=(t1(k), t2(k))代入式(10),求解并将结果标记为p=p(k+1)。
第4步:比较AP(p(k), t1(k), t2(k))和AP(p(k+1), t1(k), t2(k))。如果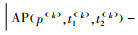
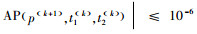
第5步:将最优解(T*, λ*, p*)代入式(5)和式(7),可得到相应的Q*和AP*。
4 算例分析在数值算例中考虑变质服从两参数Weibull分布,即θ(t)=abtb-1,其中,a是尺度参数(scale parameter),b是形状参数(shape parameter),那么有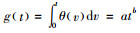
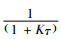
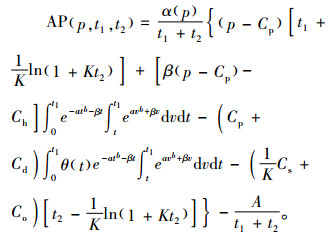
|
当Cd=0,β=0时,该模型与Dye[6]的模型一致。因此,参考Dye[6]的参数赋值,令A=250元/次,Cp=40元/件,Ch=1.5元/件/月,Cs=5元/件/月,Co=5元/件,K=0.5,α(p)=mp-n=1.6×108×p-3.21件(其中, m代表基本需求量; n表示需求的价格弹性系数),θ(t)=0.05×2×t2-1=0.1t;此外,令Cd=0.5元/件和β=0.04。以不同的初值p=[40, 50, 60, 70, 80]执行以上算法,可得到最优解为p*=59.286 2,t1*=0.711 5,t2*=0.096 8。那么有T* = t1*+ t2*=0.808 3,Q*=267.926 3,AP*=5 767.599 1。
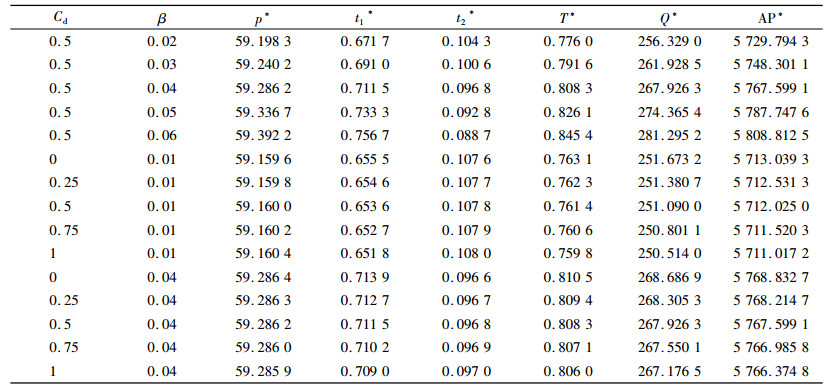
保持其他参数的取值不变,每次只改变指定参数的取值。为了观察参数β和Cd对最优解的影响,表 1给出了3种特殊情况下的模型最优解, 表 2进一步展示了最优解随β和Cd变化的灵敏度情况,表 3给出了模型中其他主要参数对最优策略及利润的影响情况。
| 表 1 参数β和Cd取值的3种特殊情况 Tab. 1 Three extreme situations for different value of β and Cd |
| 表 2 不同Cd和β取值下的最优解 Tab. 2 The results for different values of Cd and β |
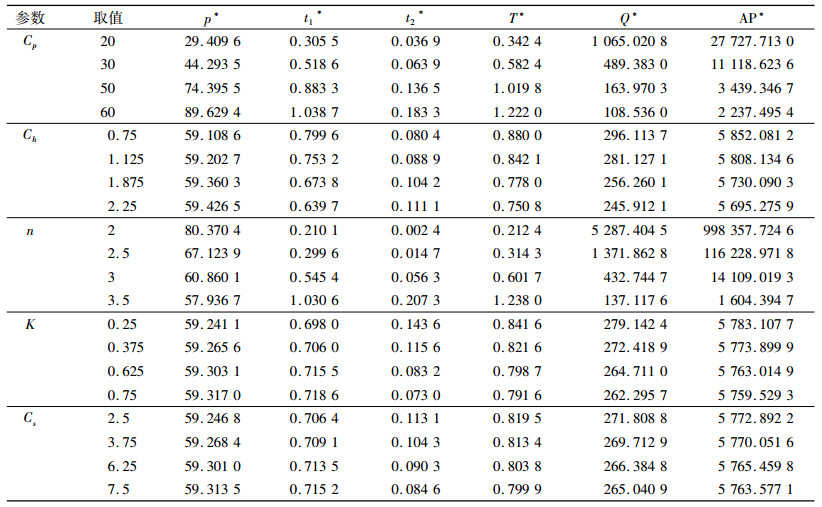
| 表 3 相关参数对最优解的灵敏度分析 Tab. 3 The sensitivity analysis of optimal solutions for some parameters |
观察表 1可以发现:与不考虑库存水平对需求的影响和物品的变质处理成本的情况(β=0和Cd=0)相比,当物品的需求受库存水平影响时(β≠0和Cd=0),最优销售价格上升、库存持有时间延长、缺货期缩短、最优订购量和利润均增加;当物品的变质处理成本存在时(β=0和Cd≠0),最优销售价格上升,库存持有时间缩短、缺货期延长、最优订购量和利润均降低。因此,如果零售商忽略库存水平对需求的影响或变质处理成本,那么所制定的销售价格将比较低。
表 2展示了最优解对β和Cd的灵敏度变化。观察可有如下发现。
1) 随着β的增大,最优销售价格p*、持有库存的时间t1*、订购量Q*和平均利润AP*均增加,最优缺货期t2*缩短。这一结果表示当库存水平对需求的影响较大时,商家应延长持有库存的时间、缩短缺货期。
2) 随着Cd的增加,最优持有库存时间t1*缩短,最优缺货期t2*延长,最优订货量Q*和平均利润AP*均降低。结果指出当单位变质处理成本增加时,商家将缩短持有库存的时间并延长缺货期以减少补货周期内物品的变质量。
3) 观察发现最优销售价格随Cd的变化而变化,但变化趋势并不是单调的。当β较小时,随着Cd的增加,最优销售价格p*上升;反之,当β较大时,随着Cd的增加,最优销售价格p*下降。由式(2)可知任意时刻的库存水平为I(t)=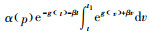
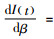
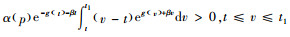
表 3给出了对模型中其它相关参数的灵敏度分析,观察可得以下结论。
1) 随着购买成本Cp的增大,最优销售价格p*和补货周期T*增大,而订购量Q*和平均利润AP*减少且对购买成本的变化具有非常敏感的负相关性。
2) 随着库存持有成本Ch的增大,最优销售价格p*和缺货时间t2*增大,库存持有时间t1*、订购量Q*和平均利润AP*减少。即当系统的持有成本较大时产品的销售定价也应相对提升,同时零售商可采用减少订购量、延长缺货期的策略来控制库存成本。
3) 随着需求的价格弹性系数n的增大,最优销售价格p*、订购量Q*和平均利润AP*减少,而库存持有时间t1*和缺货时间t2*增大。这说明,当产品具有较高的需求价格弹性系数时,为了保持一定的需求率,零售商应采用低价销售策略。
4) 随着部分延迟订购阻力系数K和缺货成本Cs的增大,最优销售价格p*和库存持有时间t1*增大,而缺货时间t2*、订购量Q*和平均利润AP*减少。这表明,当面对等待耐心较差的顾客或可替代性较强的产品时,零售商的最优策略应该是提高产品的销售定价并缩短缺货期。
5 结论本文考虑了一个在数学性质上更具一般性的易变质品的订购与定价联合决策问题,假设需求同时依赖于销售价格和即时库存水平,物品的变质率是与关于时间的一般形式的可微函数,系统允许缺货且缺货量部分延迟订购,部分延迟订购率是与顾客等待时间相关的一般形式的可微递减函数。此外,考虑已变质产品的处理成本,以系统的平均利润最大化为目标函数构建订购与定价联合决策模型。分析并证明了对于给定的销售价格,当参数满足一定条件时,使平均利润最大化的最优补货策略唯一存在;同时,对于给定的补货策略,最优销售策略也存在。此外,证明了在订购与定价联合决策下得到的最优销售价格总是大于单独进行定价决策时得到的最优价格。最后,通过算例给出模型的数值应用,并对相关参数的灵敏度进行了分析,得到以下一些重要结论:1)如果零售商忽略库存水平对需求的影响或变质处理成本,制定的销售价格将偏低;2)对需求受库存水平影响较小的产品来说,最优销售价格随着变质处理成本的增大而提高;反之,对需求受库存水平影响较大的产品来说,最优销售价格随着变质处理成本的增大而降低;3)对于需求价格弹性系数较高的产品,应采取低价销售策略;4)当面对等待耐心较差的顾客或可替代性较强的产品时,零售商的最优策略应该是提高产品的销售定价并缩短缺货期。
| [1] |
MCGILL J I, VAN RYZIN G J. Revenue management: Research overview and prospects[J].
Transportation Science, 1999, 33(2): 233-256.
DOI: 10.1287/trsc.33.2.233. |
| [2] |
GALLEGO G, VAN RYZIN G J. Optimal dynamic pricing of inventories with stochastic demand over finite horizons[J].
Management Science, 1994, 40(8): 999-1020.
DOI: 10.1287/mnsc.40.8.999. |
| [3] |
WHITIN T M. Inventory control and price theory[J].
Management Science, 1955, 2(1): 61-68.
DOI: 10.1287/mnsc.2.1.61. |
| [4] |
COHEN M A. Joint pricing and ordering policy for exponentially decaying inventory with known demand[J].
Naval Research Logistics Quarterly, 1977, 24(2): 257-268.
DOI: 10.1002/(ISSN)1931-9193. |
| [5] |
ABAD P L. Optimal price and order size for a reseller under partial backordering[J].
Computers & Operations Research, 2001, 28(1): 53-65.
|
| [6] |
DYE C Y. Joint pricing and ordering policy for a deteriorating inventory with partial backlogging[J].
Omega, 2007, 35(2): 184-189.
DOI: 10.1016/j.omega.2005.05.002. |
| [7] |
DYE C Y, HSIEH T P, OUYANG L Y. Determining optimal selling price and lot size with a varying rate of deterioration and exponential partial backlogging[J].
European Journal of Operational Research, 2007, 181(2): 668-678.
DOI: 10.1016/j.ejor.2006.06.029. |
| [8] |
SANA S S. Optimal selling price and lot size with time varying deterioration and partial backlogging[J].
Applied Mathematics and Computation, 2010, 217(1): 185-194.
DOI: 10.1016/j.amc.2010.05.040. |
| [9] |
URBAN T L. Inventory models with inventory-level-dependent demand: a comprehensive review and unifying theory[J].
European Journal of Operational Research, 2005, 162(3): 729-804.
|
| [10] |
罗兵, 杨帅, 李宇雨. 变质物品在存货影响销售率、需求和采购价均为时变时的EOQ模型[J].
工业工程与管理, 2005, 10(3): 40-44.
LUO B, YANG S, LI Y. An EOQ model for deteriorating items with time-varying demand and purchase price under stock dependent selling rate[J]. Industrial Engineering and Management, 2005, 10(3): 40-44. |
| [11] |
罗兵, 杨帅, 熊中楷. 短缺量拖后率、需求和采购价均为时变的变质物品EOQ模型[J].
中国管理科学, 2005, 13(3): 44-49.
LUO B, YANG S, XIONG Z. An EOQ model for deteriorating items with time -varying demand purchase price and partial backlogging[J]. Chinese Journal of Management Science, 2005, 13(3): 44-49. |
| [12] |
徐贤浩, 李锐娟. 存货影响销售率的短生命周期物品库存管理[J].
系统管理学报, 2007, 16(2): 135-138.
XU X, LI R. EOQ model for short-life products under stock-dependent selling rate[J]. Journal of Systems & Management, 2007, 16(2): 135-138. |
| [13] |
闵杰, 周永务. 存货影响销售率的非立即变质物品的库存模型[J].
系统工程学报, 2009, 24(2): 198-204.
MIN J, ZHOU Y. Inventory model for non-instantaneous deteriorating items under stock-dependent selling rate[J]. Journal of Systems Engineering, 2009, 24(2): 198-204. |
| [14] |
段永瑞, 李贵萍, 霍佳震. 部分延迟订购的Weibull分布变质品库存策略研究[J].
管理工程学报, 2013, 27(3): 205-213.
DUAN Y, LI G, HUO J. A study of inventory policy for perishable items with partial backlogging and Weibull distribution deterioration rate[J]. Journal of Industrial Engineering and Engineering Management, 2013, 27(3): 205-213. |
| [15] |
TENG J T, CHANG C T. Economic production quantity models for deteriorating items with price-and stock-dependent demand[J].
Computers & Operations Research, 2005, 32(2): 297-308.
|
| [16] |
HOU K L, LIN L C. An EOQ model for deteriorating items with price- and stock-dependent selling rates under inflation and time value of money[J].
International Journal of Systems Science, 2006, 37(15): 1131-1139.
DOI: 10.1080/00207720601014206. |
| [17] |
SONI H N. Optimal replenishment policies for non-instantaneous deteriorating items with price and stock sensitive demand under permissible delay in payment[J].
International Journal of Production Economics, 2013, 146(1): 259-268.
DOI: 10.1016/j.ijpe.2013.07.006. |
| [18] |
WU J, SKOURI K, TENG J T, et al. A note on "optimal replenishment policies for non-instantaneous deteriorating items with price and stock sensitive demand under permissible delay in payment"[J].
International Journal of Production Economics, 2014, 155: 324-329.
DOI: 10.1016/j.ijpe.2013.12.017. |
| [19] |
SHAH N H, SHAH A D. Optimal cycle time and preservation technology investment for deteriorating items with price-sensitive stock-dependent demand under inflation[J].
Journal of Physics: Conference Series IOP Publishing, 2014, 495(1): 1-10.
|
 2016, Vol. 19
2016, Vol. 19