装备制造业是为国民经济各行业提供技术装备的战略性产业,具有产业关联度高、吸纳就业能力强、技术资金密集等特点,是产业升级、技术进步的重要保障和国家综合实力的集中体现。由于技术的迅猛发展,产品更新换代频繁,产品的生命周期越来越短,大规模定制生产在装备制造业越来越普及。此生产模式具有诸多特点:1)装备制造系统具有复杂的随机性,为满足客户的个性化需求,系统必须通过动态配置的单元式生产,实现规模化;2)定制型的客户订单和及时化的交货期严重困扰并制约着定制型装备制造企业的生存发展,装备制造系统缓冲区容量配置是否合理影响着企业接纳订单的数量和交货期;3)定制型生产模式使装备制造系统制造单元分布越来越广,需要配置带AGV小车的物流系统运送工件。以上特点导致装备制造系统资源配置时,除了需要满足总体产能约束外,还需要组合考虑系统AGV小车及缓冲区容量优化配置。
针对系统中缓冲区容量配置问题(buffer allocation problem,BAP),国内外学者做了很多研究。文献[1]考虑具有有限缓冲区三阶段柔性流水车间的缓存优化配置问题,应用排队网建立优化模型。文献[2]考虑系统波动因素的DBR(drum-buffer-rope)瓶颈缓冲区容量设置,提出一种基于系统仿真的动态调节缓冲区容量的方法。文献[3-4]通过仿真建模对BAP问题进行实验而统计分析获得系统性能指标值的方法。文献[5-6]采用仿真的方法对多阶段每阶段具有多台设备的流水车间构建了一个仿真模型,并提出了2种启发式算法对模型中各阶段缓冲区容量值进行优化配置。文献[7]对物流系统仿真相关研究领域进行了综述,国内外学者对于生产物流系统仿真时,大多采用建立基于Petri网的网络模型的方式,而Petri网对复杂系统建模与分析时模型将变得十分复杂并产生组合爆炸。文献[8]基于eM-Plant对某制造企业的生产物流系统建模仿真,在不同的优化目标下,根据企业实际调整生产物流系统的参数和条件。文献[9]以生产线产能最大化为目标,利用仿真模型模拟AGV运行状态,并通过遗传算法确定AGV配置数量。文献[10]介绍了国内外仿真优化技术在制造系统中各个层次的应用概况。回顾相关文献,对于小规模系统的缓冲区设置问题,可以使用近似方法进行求解,如排队网模型等,而很多学者常用仿真建模进行实验进而统计分析获得系统性能指标值求解大规模的优化问题。针对装备制造系统AGV小车及缓冲区容量配置组合优化问题,发现鲜有文献进行研究。
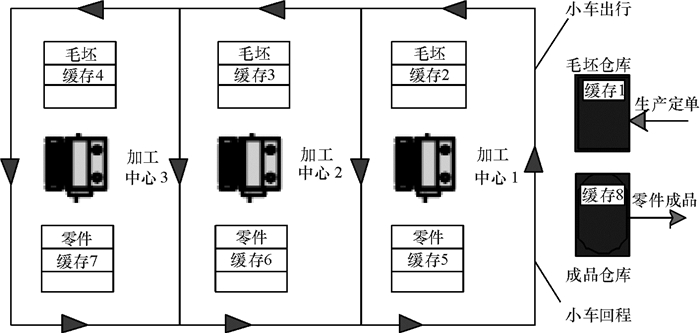
1 问题描述 1.1 问题描述具有MHS某装备制造企业智能车间具有3个加工单元,均可以加工同一类工件,每一个加工单元包含多台数控车床,加工单元前后放置毛坯缓冲区和零件缓冲区。由于加工单元在智能车间的位置分布较广,而且工件体积和重量大,需要安排自动牵引小车,完成工件的搬运。当设备加工完成后,向自动牵引小车发送卸货指令,自动牵引小车前往对应的设备进行卸载完工零件并运往缓冲区,卸货完成后再向自动牵引小车发送运货指令,自动牵引小车从缓冲区载货前往对应的设备进行上料。出于对在制品成本控制、交货期控制与缓存区场地容量的限制,存放的在制品队列是有限的,即各加工单元前后缓冲区为有限缓冲区。同时,自动牵引小车每次装载量影响着设备的利用率,因为同一时间段内可能会出现多台设备同时呼叫小车。如何配置小车及缓冲区的容量,使得制造系统的性能处于较优状态,是本文需要解决的问题。
将该制造系统简化为如图 1所示。拆分为2个子系统,具有3台同等并行机的制造单元和单AGV自动牵引小车的物流环节。只考虑一种生产定单输入系统,定单按照已知的更新过程达到毛坯仓库,若毛坯仓库已满,则拒绝新定单到达。AGV小车负责从毛坯仓库将坯料运输到加工设备前的Buffer,并接着将成品从加工设备后的Buffer运输到成品仓库。AGV小车虽然单向行驶,但有多条可能的运输路线,可以绕不同的加工中心行走,取决于前一个上料任务和下一个卸料任务,小车绕不同线运行的时间不同,且均服从已知的随机分布。各加工中心互相独立,都可以加工相同的工件,工时均服从已知的随机分布。成品被运回成品仓库后,可以看作已离开制造系统。
|
图 1 智能车间制造系统简图 Fig. 1 Intelligent Shop Manufacturing system diagram |
本文所研究的多机制造单元和单AGV运输环节组成的制造系统,除了缓冲区容量参数对系统性能有影响外,运输环节中AGV的最大容量过大,AGV运输的次数会变小,AGV利用率下降,同时也会对加工中心造成堵塞,从而导致设备利用率降低;反之,AGV最大容量过小,毛坯仓库的在制品就会积压,从而毛坯仓库接纳新定单的容量就会变小,拒绝率升高。因此,需要考虑AGV最大容量和制造单元中各缓冲区容量组合设置参数,并对其组合设置参数进行优化。AGV容量和缓冲容量组合配置优化的数学模型描述如下。
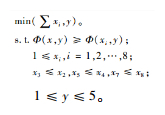
|
其中, xi为制造单元各缓冲区容量,如图 1所示的8个缓存;y为AGV最大容量,因为AGV的容量越大,价格越贵,因此只考虑到AGV最大容量为5的情况;Φ(x, y)为系统实际产量,Φ(xi,y)为系统预设产量。各加工中心线前毛坯缓存设置应不少于线后零件缓存设置。
上述目标函数是一个非线性的整数规划模型,而且,组合考虑AGV小车及缓冲区容量配置问题具有复杂的随机性,数学上的精确法求解该模型十分困难;同时,目标函数包含多维变量,存在维数灾的问题,也难以采用传统的随机模型(如排队网)描述系统的状态和行为。因此,本文拟采用仿真优化的方法,解决装备制造系统AGV小车及缓冲区容量配置优化问题。
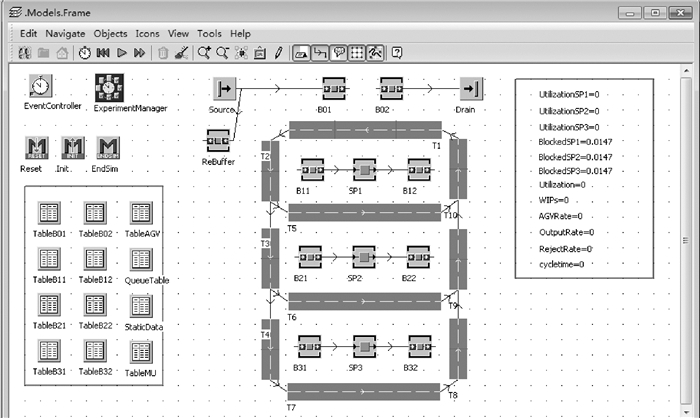
2 仿真模型的建立根据图 1所示的制造系统简图,搭建了基于Tecnomatix Plant Simulation 8.2(eM-Plant)仿真软件的仿真模型,如图 2所示。硬件基本配置为双核CPU 2.0 GHz,2 GB内存的硬件环境。根据某装备制造企业的实际情况,给出仿真模型的假设条件如下。
|
图 2 制造系统仿真模型 Fig. 2 Manufacturing System Simulation Model |
假设1 考虑一种工件输入系统,工件到达互相独立,且服从均值为λ的泊松分布。
假设2 生产环节有3台加工中心,分别只能同时加工一个工件,其加工时间都是互相独立,均服从速率为μ1的指数分布(包括装夹时间、准备时间)。
假设3 每台加工中心可用性比率为90%,即设备失效率为10%,平均修复时间MTTR (mean time to repair)为3 h,故障持续时间服从爱尔朗分布。
假设4 制造单元服务原则为先到先服务,服从后阻塞机制,各毛坯暂存区和各零件暂存区是有限容量的。
假设5 考虑一台AGV小车,最大容量为5,每次运行之间是互相独立,绕3条线运行的平均运送时间不同,且均服从指数分布.
假设6 小车配送原则为负荷均衡原则,不考虑小车的装卸时间。
根据以上假设,仿真模型中系统由物流环节和制造单元组成,如图 2所示。工件由订单源产生,订单源按照泊松分布平均每小时产生λ个任务,只输入一种订单,然后进入毛坯中心库区B01,由AGV小车运输至其中一个加工中心(SP1、SP2、SP3)前的线前暂缓区(B11、B21、B31)等待加工,完工后的零件将进入加工中心后面的线后成品区(B12、B22、B32),等待AGV小车将其运回零件中心库B02,然后离开系统。AGV小车配送原则为自动循环运行,出行时AGV小车为线前暂缓区(B11、B21、B31)中最少工件数的暂缓区服务,装载工件时小车按照将毛坯最少的暂存区补满或小车最大装载量原则,回程时小车为零件数最多的暂存区服务,装载零件时按照最大量装载原则。3台加工中心的加工时间都服从指数分布,总的处理速率为μ个/h,失效率均为10%,MTTR为3 h。AGV小车绕3条线运行的平均运送时间不同,且均服从指数分布。其中图 2所示的



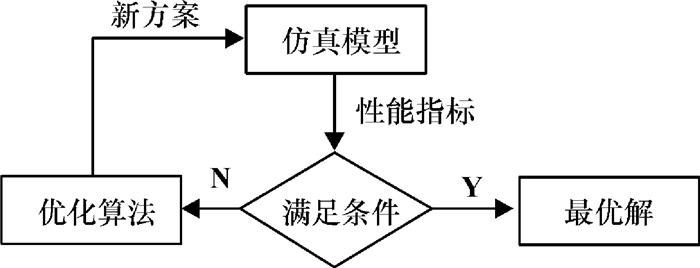
仿真优化的基本原理,利用仿真模型来替代传统优化模型中的目标函数和约束条件,由优化算法产生一组初始解,将该初始解输入到仿真模型,仿真一段时间后,得到这组解的性能指标,将这组解及其性能指标输入到优化算法中搜索迭代得到一组新解,这组新解比迭代前的解性能更优,再将新解导入到仿真模型,如此反复直到性能指标满足要求,输出最优解[11],如图 3所示。
|
图 3 仿真优化原理图 Fig. 3 Simulation and optimization schematics |
任务拒绝率是企业拒绝新订单的比率,任务拒绝率越高,意味着企业失去更多的订单,从而企业总产值下降,这是企业不希望看到的结果。以任务拒绝率为优化目标的优化方法如图 4所示,仿真之前给定一个任务拒绝率的期望值,仿真时设定AGV容量和各缓存初值,AGV容量从1开始一直到5。设图 2中缓存B01、B11、B21、B31、B12、B22、B32初值为N01-32取值参考表 1所得实验结果,缓存B01~B32每一次仿真的实际容量为B01-32,AGV小车的容量为C,图 4~图 6参数变量表示含义相同。然后进行一次仿真,观察所得的任务拒绝率是否达到预设的期望值,如果符合则得到的1组AGV容量与各缓存值为仿真结果,直到5种AGV容量都仿真完成,否则将毛坯仓库缓存增大并进行一次新的仿真,直到任务拒绝率达到预设的期望值。
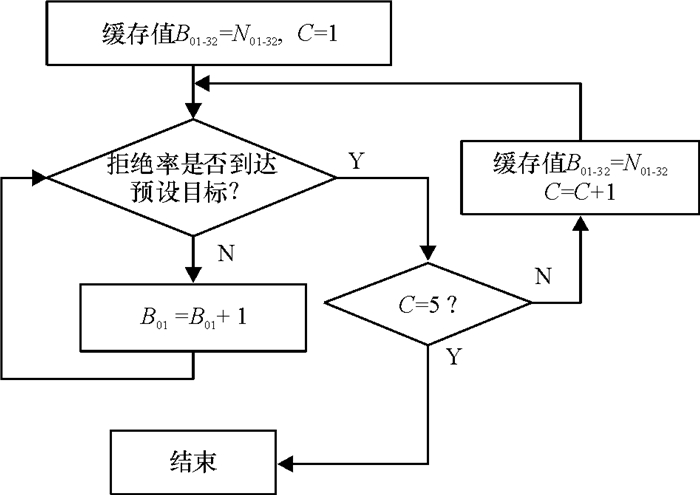
|
图 4 以任务拒绝率为目标的优化方法 Fig. 4 Task reject rate optimization goals |
| 表 1 无限缓存下各缓存平均队长 Tab. 1 The average queue length of the cache |
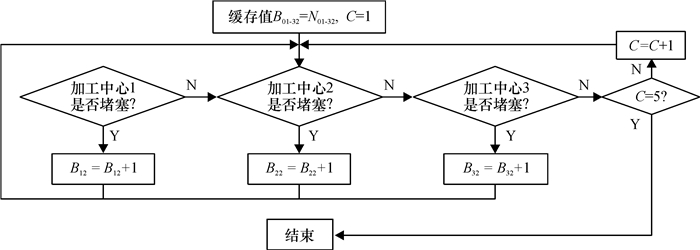
|
图 5 以设备堵塞率为目标的优化方法 Fig. 5 Equipment utilization optimizing goal |
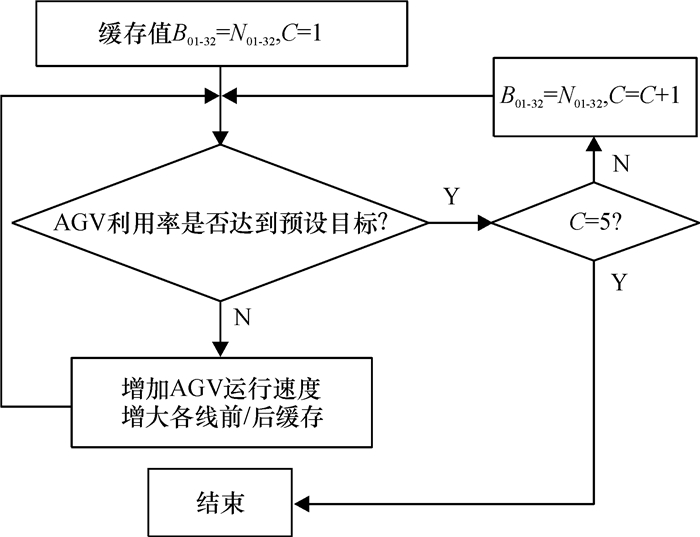
|
图 6 以AGV利用率为目标的优化方法 Fig. 6 AGV utilization optimizing goal |
对于设备利用率,企业因为对设备投入了很大的成本,特别是一些先进的加工中心,企业特别希望设备利用率越高越好,才不会造成产能浪费。文献[6]在仿真优化过程中发现当缓存不够大时,设备的利用率不够高的一个主要原因是由于缓存过小造成了堵塞。图 1所示的制造系统简图,每一个加工中心的线后零件缓存饱和之后,加工中心就会被堵塞,无法进入线后零件缓存区,完工的零件只能在加工中心上等待,直到下一级出现空位,等待过程将严重影响设备的利用率。以设备利用率为优化目标的优化方法如图 5所示,AGV容量与各缓存参数设置和上述以任务拒绝率为目标的优化方法相同,然后进行一次仿真,观察3个加工中心是否堵塞,如果堵塞则增加该加工中心的线后缓存直到该加工中心不再堵塞,3个加工中心都不堵塞,就可以得到1组AGV容量与各缓存值的仿真结果,然后再进行下一种AGV容量的仿真实验,直到5种AGV容量全部仿真完成实验结束。
对于AGV利用率,AGV是制造系统中的运输环节,如果运输环节的效率太低,系统中的工件不能及时被运输到加工中心上,导致设备闲置,而且完工的零件不能被及时运回成品仓库,也会对设备造成堵塞。以AGV利用率为优化目标的优化方法如图 6所示,AGV容量与各缓存参数设置和上述以任务拒绝率为目标的优化方法相同。仿真前预设AGV利用率的期望值,然后进行一次仿真,观察所得AGV利用率是否达到期望值,如果不能达到,则增加AGV运行速度,同时增大各线前、线后缓存,然后再进行一次仿真,直到所得仿真结果达到期望值。如果符合可以得到1组AGV容量与各缓存值的仿真结果,然后再进行下一种AGV容量的仿真实验,直到5种AGV容量全部仿真完成实验结束。AGV利用率在现实生产中要达到100%的可能性很小,因为任务的到达和加工过程的时间都是随机的,AGV每次满载的机率很低,因此AGV利用率预设期望值为90%。
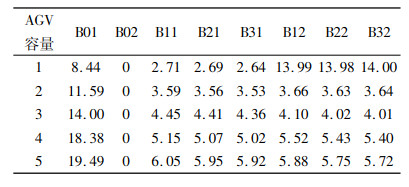
4 实例与结果分析 4.1 仿真实验设计为了验证仿真模型的有效性,针对AGV每一种容量与缓存组合设置参数设计试验方案。根据前文的数学模型,考虑AGV的5种容量,分别是1、2、3、4、5。基于图 2所示的仿真平台,比较分别以任务拒绝率为0、设备堵塞率为0和AGV利用率为90%3种目标的仿真优化方法,选取一种结果更优的方法,得到AGV每一种容量下缓存设置参数。最后再比较5种容量与缓存组合设置的参数,得到一组设置参数使得系统的性能指标更优。因为任务的到达和加工速率都是随机分布,为了得到能准确描述系统的仿真结果,根据大数定理,每次仿真的时间设置为1 000 d,仿真结果由10组相同参数独立随机仿真试验的结果求均值得到。每一种AGV容量下各缓存的初值,通过预设各缓存容量为∞,仿真至系统稳态后得到各缓存的平均队列长度,以此作为缓存初值设置依据,如表 1所示。
从表 1可以看出,零件成品仓库B02缓存的平均队长始终为0,这是因为零件被AGV运回B02后马上离开系统,对系统不会造成堵塞影响。因此,零件成品仓库B02缓存在仿真试验时设置为∞。
针对上述3种方法,进行仿真可得到每一种AGV容量与各缓存组合设置参数的结果,如表 2所示。其中, 方法1表示以任务拒绝率等于0为目标;方法2表示以3个加工中心堵塞率等于0为目标;方法3以AGV利用率大于等于90%为目标。设备堵塞率、AGV利用率和任务拒绝率,具体实验参数设置初始值如表 2所示。每一种试验的输入速率λ表示定单输入速率,λ=0.9个/h;处理速率μ表示3个加工中心总的处理速率,μ=1个/h;AGV容量初始设置为1,仿真过程一直仿真至5;各缓冲区容量参数设置初值参考表 1所得的平均队长。
| 表 2 实例数据 Tab. 2 Instance data |
根据表 2所示的实例数据设置,在仿真模型上进行仿真,得到如表 3~表 5所示3种方法的优化结果。
| 表 3 任务拒绝率为目标的实验结果 Tab. 3 Experimental results for task rejection rate |
| 表 4 设备堵塞率为目标的实验结果 Tab. 4 Experimental results for equipment utilization rate |
| 表 5 AGV利用率为目标的实验结果 Tab. 5 Experimental results for AGV utilization |
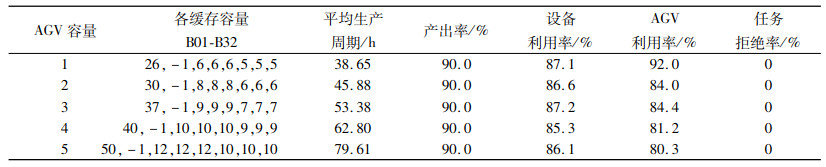
表 3是任务拒绝率等于0为目标的优化方法结果,表中可以看出,5种AGV容量以及各缓存区容量组合参数中,当AGV小车容量为1时的组合参数,系统的平均生产周期最少,即企业的交货期最短,并且AGV小车利用率最高,而设备利用率略低于AGV容量为3时的结果。因此AGV小车容量为1的AGV容量以及各缓存区容量组合参数的设置为5种参数设置中最优。
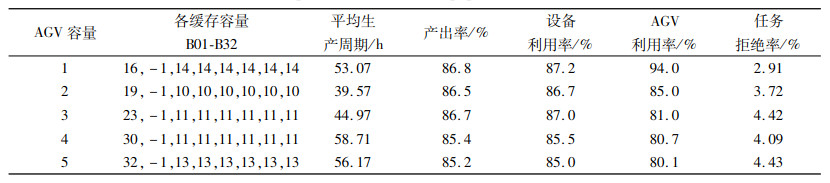
表 4是设备堵塞率等于0为目标的优化方法结果,表中设备利用率并没有因设备堵塞率为0而达到100%,这是因为设备虽然不存在堵塞,但是设备仍存在闲置的可能。5种AGV容量以及各缓存区容量组合参数中,第2组参数的系统平均生产周期最少,即企业的交货期最短,而产出率和设备利用率指标只比第1、3组的系统指标略低,虽然第1组参数所得的AGV利用率也是最高的,但第1组参数系统的平均生产周期比第2组要长很多,即交货期长,这使得企业的竞争力大大降低。因此,综合系统指标考虑,AGV小车容量为2的AGV容量以及各缓存区容量组合参数的设置为5种参数设置中最优。
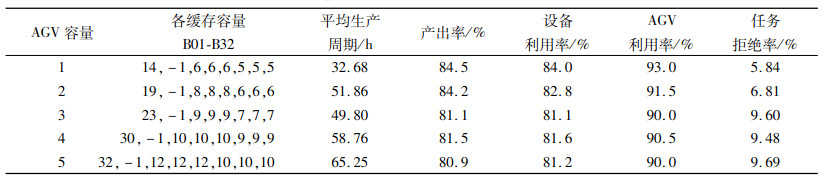
表 5是AGV小车利用率大于等于90%为目标的优化方法结果。表中可以看出,5种AGV容量以及各缓存区容量组合参数中,当AGV小车容量为1时的组合参数,AGV小车利用率最高,系统的平均生产周期最少,即企业的交货期最短,设备利用率、产出率最高,即系统的产能最高。因此AGV小车容量为1的AGV容量以及各缓存区容量组合参数的设置为5种参数设置中最优。
综合表 3~表 5,3种优化方法的最优组合以及所得的系统性能指标如表 6所示。从表 6数据结果显示,第1种优化方案中,平均生产周期较其他2种方案而言不是最短的,但产出率和设备利用率最高,任务拒绝率为0。这种方案下虽然企业的交货期较长,但是企业的产能却是最高的。优化方案2,平均生产周期较其他2种方案而言最少,即企业的交货期最短,这种方案下企业的竞争力较大,但是各缓冲区容量配置却是3种方案中最大的,即缓冲区的面积较大,车间建设成本也较其他两种方案而言要高。第3种优化方案是以运输环节中AGV利用率为目标所得的结果,这种方案的产出率、设备利用率略低于其他两种方案,但缓冲区容量的设置也是3种方案中最少的,即车间建设成本的投入少。
| 表 6 3种优化方法最优参数设置及实验结果 Tab. 6 Optimal parameters setting and experimental results of three kinds of optimization methods |
设备的利用率是企业产能的最重要指标。从表 6实验结果可以看出,要提高设备利用率,企业需要争取更多的订单量,并具备可容纳大量毛坯中心库区;而加工设备前后的缓存区容量不能过大,避免设备出现过多空闲或者被堵塞状态;AGV组成的运输系统,小批量、多批次的运货策略,制造单元的设备利用率最高,运输的效率也是最高。
取表 6中优化方案1,并通过500组仿真实验分析装备制造系统性能指标变化情况,根据得到的500组仿真数据,取其中随缓存增加而单调变化的“任务拒绝率”和“产出率”进行分析,2项指标拟合出的多项式曲线如图 7所示,其中横坐标即为一组试验中不同缓存组合总数。随着各级缓存的增加,“任务拒绝率”在前期出现快速下降的趋势,后期下降速率逐渐变缓并趋于0;而“系统产出率”随着各级缓存的增加则呈现单调上升的趋势,前期出现快速上升的趋势,后期上升速率逐渐变缓并趋于0.9,即趋于系统输入速率。
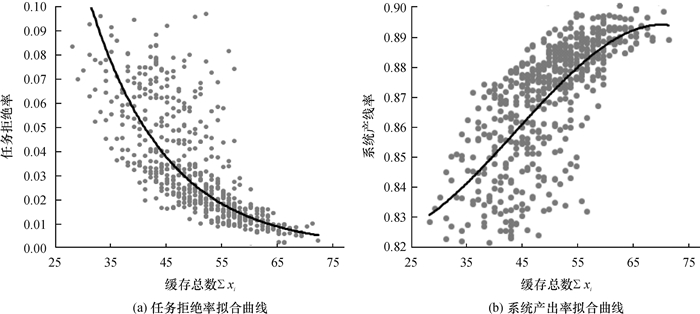
|
图 7 仿真结果拟合曲线 Fig. 7 Simulation result fitting curve |
本文通过建立仿真模型,应用3种仿真优化方法,对具有MHS的装备制造系统AGV小车及缓冲区最大容量配置问题进行了仿真优化。通过仿真分析,得到了3种优化方案下的优化结果,根据仿真优化结果对上述3种方法进行了分析与比较,3种优化方法所得的AGV小车及缓冲区配置方案适用于不同的车间配置与企业决策。该仿真优化模型可为企业配置AGV小车及缓冲区最大容量提供一种有效的方法,同时为制造系统排队网研究提供了大量的数据支持。
| [1] |
张惠煜, 康伟成, 毛宁, 等. 面向定制生产系统的缓冲区优化配置方法[J].
工业工程, 2014, 17(5): 85-92.
ZHANG Huiyu, KANG Weicheng, MAO Ning, et al. Buffer optimization configuration method for customized manufacturing system[J]. Industrial Engineering Journal, 2014, 17(5): 85-92. |
| [2] |
徐云天, 张力菠. 考虑系统波动因素的DBR瓶颈缓冲区容量设置[J].
工业工程, 2014, 17(6): 24-29.
XU Yuntian, ZHANG Libo. Determination of constraint buffer size for drum-buffer-rope considering system′s fluctuation factor[J]. Industrial Engineering Journal, 2014, 17(6): 24-29. |
| [3] |
SINGH A, SMITTH J M. Buffer allocation for an integer nonlinear network design problem[J].
Computers and Operations Research, 1997, 24(5): 453-472.
DOI: 10.1016/S0305-0548(96)00068-8. |
| [4] |
HASKOSE A, KINGSMAN B G, WORTHINGTON D. Performance analysis of make-to-order manufacturing systems under different workload control regimes[J].
International Journal of Production Economics, 2004, 90(2): 169-186.
DOI: 10.1016/S0925-5273(03)00052-5. |
| [5] |
康伟成, 俞爱林, 黎展滔. 基于仿真的多级流水车间缓冲区配置优化[J].
机电工程技术, 2013, 42(11): 1-5.
KANG Weicheng, YU Ailin, LI Zhantao. Simulation-based buffer allocation optimization for multistage flow-shop[J]. Mechanical and Electrical Engineering Technology, 2013, 42(11): 1-5. DOI: 10.3969/j.issn.1009-9492.2013.11.001. |
| [6] |
李翔, 陈庆新, 毛宁, 等. 多级流水线车间缓存设置参数仿真优化[J].
模具工业, 2012, 38(7): 1-6.
LI Xiang, CHEN Qingxin, MAO Ning, et al. Simulation optimization of buffer allocation parameters in multistage flow shop[J]. Mould Industry, 2012, 38(7): 1-6. |
| [7] |
李永先, 胡祥培, 熊英. 物流系统仿真研究综述[J].
系统仿真学报, 2007, 19(7): 1411-1416.
LI Yongxian, HU Xiangpei, XIONG Ying. Overview on logistics system simulation[J]. Journal of System Simulation, 2007, 19(7): 1411-1416. |
| [8] |
杨堃. 基于eM-Plant的生产物流系统仿真与应用[J].
工业工程, 2010, 13(5): 95-100.
YANG Kun. eM-Plant-Based simulation and optimization of steel tube production process:a case study[J]. Industrial Engineering Journal, 2010, 13(5): 95-100. |
| [9] |
张远春, 范秀敏, 驹田邦久. 基于仿真优化的多种类型AGV数量配置优化方法[J].
中国机械工程, 2011, 22(14): 1680-1685.
ZHANG Yuanchun, FAN Xiumin, KOMADA Kunihisa. Multi-types AGVs quantity configuration optimization based on simulation optimization[J]. China Mechanical Engineering, 2011, 22(14): 1680-1685. |
| [10] |
王国新, 宁汝新, 王爱民, 等. 仿真优化在制造系统中的应用现状及发展趋势[J].
系统仿真学报, 2008, 20(1): 1-6.
WANG Guoxin, NING Ruxin, WANG Aimin, et al. Present application situation and trends of simulation optimization in manufacturing system[J]. Journal of System Simulation, 2008, 20(1): 1-6. |
| [11] |
王国新, 宁汝新, 王爱民. 基于仿真的生产调度优化技术研究[J].
计算机集成制造系统, 2007, 13(7): 1419-1427.
WANG Guoxin, NING Ruxin, WANG Aimin. Production optimal scheduling technology based on simulation[J]. Computer Integrated Manufacturing Systems, 2007, 13(7): 1419-1427. |
 2016, Vol. 19
2016, Vol. 19