2. 湖南工学院,湖南 衡阳,421002;
3. 华南理工大学广州学院 计算机工程学院,广东 广州,510800;
4. 南华大学 计算机科学与技术学院,湖南 衡阳,421001
2. Hunan Institute of Technology, Hengyang 421002, China;
3. School of Computer Engineering, Guangzhou College of South China University of Technology, Guangzhou 510800, China;
4. College of Computer Science and Technology, University of South China, Hengyang 421001, China
核电厂数字化规程布局指在事故状态下,各规程在某一时间如何定位到其中一个计算机屏上, 使同一操纵员在屏之间的移动距离最少, 进而减少事故恢复时间,达到减少人因事故的目的。事故处理过程中,规程及信息均呈现在不同的显示屏上, 操纵员需在显示屏之间进行移动来执行或恢复事故。移动路径主要受2个方面影响[1]:1)显示屏之间的距离;2)起始位置及目标位置的定位方式。以影响移动路径的二个因素为切入点,以减少操纵员在屏之间的移动距离为目标, 本文研究了数字化规程布局的最短移动路径算法,从而减少操纵员事故恢复的时间。
1 数字化规程在屏之间布局方法及评价 1.1 规程布局流程本研究利用人工神经网络的处理机制,对数字化规程在屏之间布局的方法进行详细描述。人工神经网络是基于大脑神经元结构对自然界事物反应及处理过程的信息模型[2]。根据神经网络的基本理论,本文提出的数字化规程在屏之间布局过程由3层组成。第1层为参数输入层, 包括人的影响因子及各规程的执行时间;第2层为隐含层, 包括功能函数和人因可靠性评价;第3层为输出层, 输出结果为数字化规程在屏之间布局的人因可靠性。图 1显示了规程在屏之间布局的流程。

|
图 1 核电厂数字化规程在屏之间布局流程 Fig. 1 The layout flow chart about digital regulations among displays in nuclear power plant |
目前为止, 最短路径算法主要有[3]:1)深度与宽度优先搜索算法;2)启发式算法; 3)动态规划方法;4)标号法;5)迭代法;6) Dijkstra算法;7) Floyd算法等等。本文以Floyd算法为基础,对核电厂数字化规程在屏之间的布局提出了动态标识最短移动路径算法。
1.2.1 问题描述当事故发生时, 主控室同一操纵员需在多个显示屏之间不断移动来获取参数信息, 且须按照规程序列一步一步完成任务。这些事故规程动态地呈现在不同显示屏上, 操纵员需在不同屏之间进行画面切换, 且需按处理流程进行操作。这就涉及到操纵员需在不同显示屏之间进行移动才能顺利完成操作, 因此,操作过程完成每一步规程的执行时间包括移动时间和处理时间。需要解决的是如何使执行每一步规程的移动时间最小, 也即是规程如何定位到某个显示屏上。该布局过程要注意几点:1)显示屏位置是固定不变的, 信息分配则是动态的;2)有些显示屏上的规程或信息在某时刻可以被其他规程或信息覆盖, 有些则不能;3)有些显示屏上的规程或信息可以暂时被其他规程或信息覆盖, 但不久后需进行恢复。
上述描述的这个问题, 实际就是最短路径的动态规划问题。当规程切换到某个显示屏并完成相应的操作时, 需确定下一规程应布局在哪个显示屏上以使操纵员移动距离最短, 移动距离最短意味着移动时间最小, 移动时间越小越能保证操纵员有更多的时间去处理事故,从而提高事故处理的可靠性。这一过程简单来说就是规程或信息的布局影响移动时间, 移动时间又进一步影响人因事件的可靠性, 因此,该问题可看成是求动态过程中的最短路径问题。
1.2.2 动态标识最短移动路径算法的提出为描述方便,把每个显示屏看成是图形结构中的一个节点。1)对每个节点进行标识, 若为true, 则表明从其他节点不能到达该节点, 若为false, 则能够从其他节点到达该节点或从该节点本身到达本身。每个节点的标识为true或false是动态变化的, 每执行完一个规程画面或辅助信息画面, 就需判断每个节点标识是否变化, 节点标识的改变完全由其信息特征决定。2)所有节点需分为2组, 一组用来存放标识为true的节点, 另一组用来存放标识为false的节点。3)节点之间的连接权重指距离权重, 用Wij表示(节点i与节点j之间的权重), 若i=j, 则Wij=0。
算法具体执行过程如下。最开始可以任意假定一个节点的标识为true, 为描述方便,这里假设v0的标识为true, 这时第1组仅包含节点v0, 用Group1={v0}表示(最初始节点的标识也可以为false, 那么此时Group1={ }), 其余的节点属于第2组, 用Group2={v1, v2, …,vn}表示, 用Dis[vi, vj]表示从节点vi到vj的距离,这里所指的距离并非节点之间的实际距离,而是指节点之间的距离间隔数。之后从第2组中选择一个节点,使从v0出发到该节点的距离最小,假设该节点为v3, 需满足Dis[v0, v3]= min(Dis[v0, vj])。同时要动态生成权重Wij, 还需评估v3节点上的信息特征, 决定是否改变其标识, 若变为true, 则节点v3进入第1组, 同时需从第2组删除v3, 若标识无改变,则v3仍留在第2组(若是这种情况,下次到达的目的地就是节点本身v3);另一方面,需评估第1组中所有节点, 决定其节点标识是否发生改变, 若某个节点标识发生改变, 则该节点需进入第2组, 同时把其从第1组中删除;类似,第2次执行过程同样需从第2组中选择一个最小的Dis[vi, vj]值, 如果上一次节点的标识仍为false, 那么该次规程画面布局目的地就为同一节点, 则Dis[vi, vj]=0, Wij=0, 否则, 若上一次节点的标识为true, 则用上述描述的方法继续执行下去, 不断循环, 直到事故完全得到恢复为止。
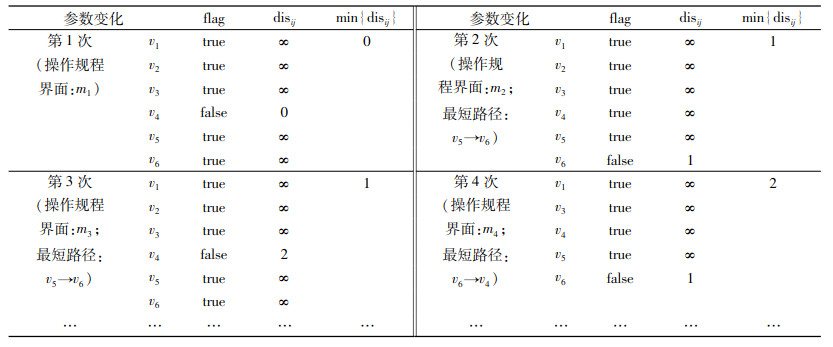
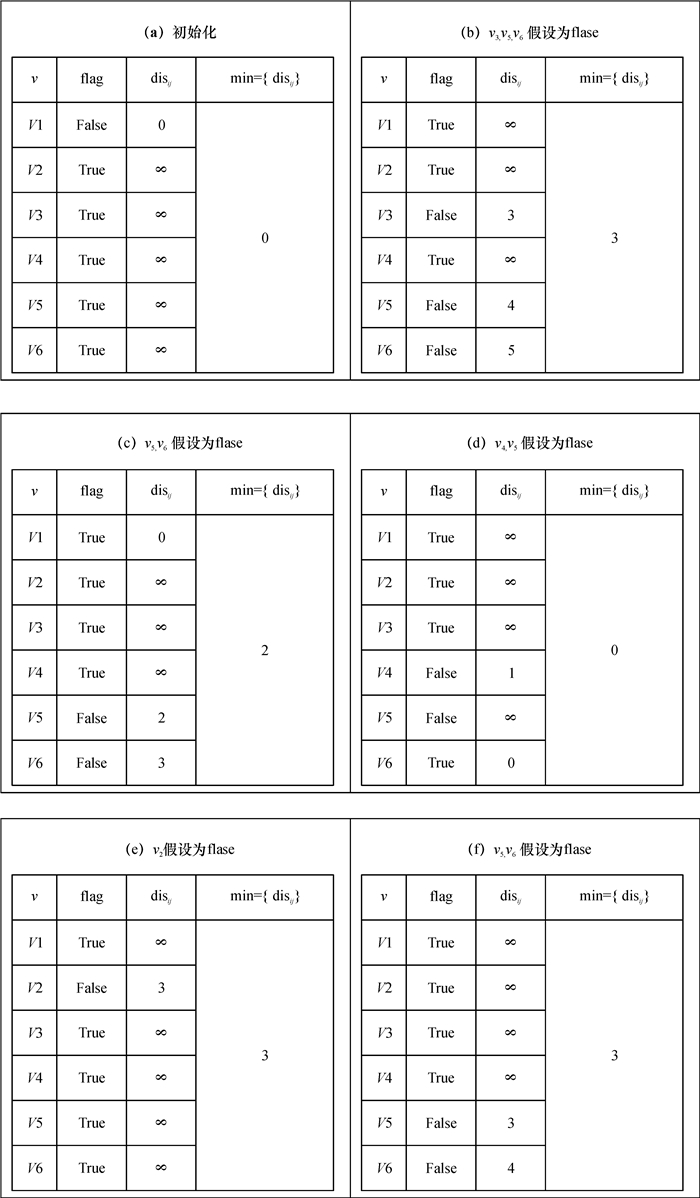
1.2.3 动态标识最短移动路径算法的执行过程假使有6个节点, 用数组set存放每对节点的路径值, 节点用v表示, 标识用flag表示, 节点i与节点j之间的距离用disij表示, 执行次数为5次, 具体执行过程如图 2。
|
图 2 动态标识最短移动路径算法的执行过程 Fig. 2 The performing process of shortest moving path algorithm with dynamic flag |
从图 2的求解过程可以看出:规程布局形成的最短距离分别为0、3、2、0、3、3;规程画面最开始显示在第1号屏上, 此后在执行其他5个规程过程中, 规程画面依次显示在第3、第5、第5、第2、第5号显示屏上。
1.2.4 算法性能分析及代码描述假设事故需要执行n次, 节点数为v, 边的数量为e。该算法复杂度主要花费在扫描节点数组以找出节点之间的最短距离, 显然,每一次寻找节点之间最短距离的执行次数为v, 那么,执行n次的运行次数为n×v, 从而将花费O(|v×n|)代价去查找节点之间的最短距离;另一方面, 在执行任务前, 需给所有节点及节点之间的边赋值, 此过程的执行次数为O(|e2|),因此, 该算法总的复杂度为O(|v×n|+|e2|)。
算法的伪代码如下。
1) 将节点初始化并分为2组。
V1=True;v2, v3, …,vn=false;
Set:Group1={v1}; Set:Group2={v2, v3, …,vn}。
2) 对边的权重赋初值
For a=1;a≤|e|; a++) For (b=1;b≤|e|; b++) Dis[i, j].weight=adjacent[i, j]。
3) flagV1=true;i=1。
4) 重复执行n步,直到事故完成。
For(k=1;k≤n; k++) {min=赋一个很小的初始值;If(flagvk=false) min(dis[k, j])=0; Else{For(j=1;j≤v; j++)
{If(dis[k, j] < min) Min=dis[k, j];
移动到节点Vj; T[k, j]=获取动态时间;k=j; If (vk=true)
{Group1_nodes=Group1_nodes+{vk}; Group2=all_nodes-Group1_noses; } Else vk∈Group2;
//对第1组的各个节点进行判断, 识别节点的标识是否发生变化
for(i=1;i≤Group1_nodes; i++) if(vi=false){Group1_nodes=Group1_nodes-{vi};
Group2_nodes=Group2_nodes+{vi}; }}}。
1.3 规程布局评价方法本研究中, 规程布局性能评价采用作者前期的研究成果,即:利用带时间参数的人因可靠性神经网络方法,该评价方法如下[4]。
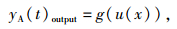
|
(1) |
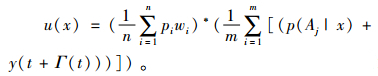
|
(2) |
这里, yA(t)output是某事故下经神经网络变换得到的最终人因失误率;wi是神经网络各神经元的连接权重,pi表示初步人因失误率,wi和pi的基础数据详见已有研究[4-7];y(t+γ(t))表示完成所有规程情况下的初步人因失误率;t+γ(t)表示事故状态下第j次操作过程的执行时间, t表示在屏之间的移动时间, 需通过动态标识最短移动路径算法获得, γ(t)表示操纵员完成第j次操作的时间, n为人的影响因子个数。式(2)具体计算过程见作者前期研究[8]。
2 事例分析 2.1 事例描述本实验以核电厂SGTR(蒸汽传热管断裂事故)为背景。实验过程使用了2台电脑及12个显示屏,事故规程模拟画面均由作者通过Visual studio basic.net工具开发得到。
实验过程需获得的执行时间包括在显示屏之间的移动时间及处理规程或信息的时间。在得到时间后, 须对规程布局过程的性能评价其人因失误率,采用MATLAB完成人因失误率的计算工作。
2.2 规程布局过程及性能评价1) 本实验对SGTR中的规程进行模拟, 根据本研究提出的动态标识最短移动路径算法对数字化规程如何在不同显示屏之间进行布局, 得到整个事件时间参数t。试验起始操作屏为第4屏, 试验过程进行了36次数字化规程画面的布局,除此之外,还进行了34次辅助画面调用。
表 1中,参数disij表示当前显示屏与显示下一规程的显示屏之间的距离, 为简单起见, 距离用显示屏之间的间隔数来表示;min{disij}表示取disij的最小值。由于执行次数较多,这里只列出几次数字化规程布局参数变化情况,如表 1。
| 表 1 规程布局过程及参数变化表 Tab. 1 the procedure layout process and parameters varing table |
实验过程经历了36步, 实验获得的数字化规程在显示屏之间布局的顺序依次为v4, v6, v6, v4, v6, v6, v4, v5, v5, v6, v6, v4, v5, v5, v3, v6, v4, v5, v4, v4, v5, v4, v5, v5, v6, v6, v5, v2, v5, v2, v1, v1, v2, v5, v4, v6。
2) 用于评价规程布局的人因失误率。
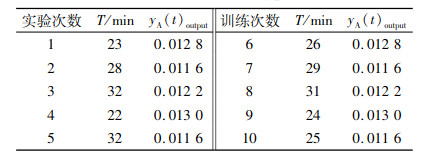
根据动态标识最短移动路径算法及式(2),表 1分别获得了10次模拟的总时间T及用于性能评估的人因失误率。根据本实例的具体情况, 不管实验次数多少,规程布局基本上是一致的, 因此在模拟实验中, 多次实验过程的规程布局基本上是相同的, 且只有按这样的顺序布局在屏上, 操纵员的移动路径才会最少, 其他9次实验不再列出规程布局及参数变化过程。10次模拟实验得到的各自执行时间及人因失误率见表 2。
| 表 2 SGTR事件模拟训练过程的时间及人因失误率 Tab. 2 The time and human error probability in the SGTR simulated training process |
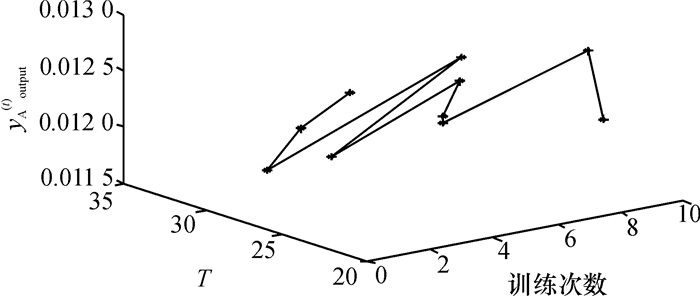
为更清楚表达执行时间与人因失误率之间关系的变化曲线,可根据实验得到的数据, 用一个图来表示,图形如图 3所示。
|
图 3 SGTR实验过程失误率、执行时间的变化曲线图 Fig. 3 The varing curve graph of error probabilities and performing time for SGTR experimental process |
显然,从图 3可以看出, 1)失误率不断变化,说明提出的方法灵敏度高;2)失误率变化幅度不太大,说明该方法比较稳定;3)尽管训练时间有差别,但失误率变化与时间变化不成正比,这说明只要按提出的算法进行规程自动布局,失误率变化不会很明显,因此失误率很大程度上由规程布局决定,更说明该算法具有一定的现实意义。
3 小结本文在Floya算法基础上,结合人因可靠性理论,提出了核电厂数字化规程在屏之间的布局方法, 解决了核电厂数字化人机界面事故规程在显示屏之间的自动布局方法,使同一操纵员在屏之间移动距离最小,进一步减少操纵员处理事故的时间,从而彰显了该算法的优势。且通过实验分析验证了该方法能很好地应用到数字化系统下规程的自动布局,能减少处理事故的时间,提高了系统的安全性。
本研究也存在一些缺陷, 例如人的影响因子还需进一步完善,可能会存在偏差。后续拟通过模拟机实验对方法进行完善并在其他数字化领域进行应用与推广。
| [1] |
SEIDLER K, WICKENS C. Distance and organization in multifunction displays[J].
Human Factros, 1992, 34(5): 555-569.
DOI: 10.1177/001872089203400504. |
| [2] |
ELHEWY A H, MESBAHI E, PU Y. Reliability analysis of structures using neural network method[J].
Probabilistic Engineering Mechanics, 2006, 21(1): 44-53.
DOI: 10.1016/j.probengmech.2005.07.002. |
| [3] |
张建军, 杜莉. 最短路径算法的分析与优化[J].
北京工业职业技术学院学报, 2009, 8(3): 26-31.
ZHANG Jianjun, DU li. Analysis and optimization of A lgorithm for F inding shortest path[J]. Journal of Beijing Polytechn Ic College, 2009, 8(3): 26-31. |
| [4] |
何旭洪, 黄祥瑞.工业系统中人的可靠性分析:原理、方法与应用[M].北京:清华大学出版社, 2007.
|
| [5] |
MASSIMO B. Assessment of human reliability factors:A fuzzy cognitive maps approach[J].
International of Industrial Ergonomics, 2007, 37: 405-413.
DOI: 10.1016/j.ergon.2005.12.009. |
| [6] |
SHEN S H, SMIDTS C, MOSLEH A. A methodology for collection and analysis of human error data based on a cognitive model:IDA[J].
Nuclear Engineering and Design, 1997, 172: 157-186.
DOI: 10.1016/S0029-5493(97)00002-2. |
| [7] |
LI J A, YUE W, LAI K F, LIU K. Reliability estimation and prediction of multi-state components and coherent systems[J].
Reliability Engineering & System Safety, 2005, 88(1): 93-98.
|
| [8] |
ZHANG L, JIANG J J, WANG Y Q, et al. Reliability estimation of neural networks with human factors under emergency of nuclear power plant[C].2011 IEEE International Conference on Computer Science and Automation Engineering. ShangHai:2011.
|
 2016, Vol. 19
2016, Vol. 19