随着Web2.0的不断发展,人们越来越习惯于从社交网络中获得服务,如何高效地搜索并获得服务是一个非常有意义的课题。为了满足用户的各种需求,出现了推荐系统,推荐系统被广泛应用于为用户提供高质量及有效的推荐[1]。推荐系统的方法分为基于内容的推荐,协同过滤推荐,基于知识的推荐和混合推荐的方法,其中协同过滤方法是应用最广泛的方法[2],电子商务环境下为用户提供高效的推荐是非常有意义的课题,但稀疏性和冷启动问题严重影响着推荐算法的质量,同时在社交网络中,一些商家为了利益,容易形成欺诈行为。
社交网络在不断拓展,信任被逐渐引入推荐系统。基于信任的推荐方法虽然有较好的推荐效果,但存在因素单一性,社交网络用户细分等问题[3]。
本文将针对稀疏性和冷启动问题,同时结合社交网络中的信任和相似度,融入到随机游走算法中,并在试验中验证算法的有效性。
协同过滤推荐算法主要有基于User的CF算法[4]和基于Item的CF算法[5],算法主要依靠计算用户或项目间相似度,得到最近邻居集合,通过邻居集合来获得推荐,但算法面临稀疏性和冷启动问题,覆盖率低。
信任逐渐被引入推荐系统来做高质量的推荐,结合信任的推荐系统认为人们更愿意考虑朋友的推荐,目前结合信任的推荐系统已经有了广泛研究与应用。Epinions[6]比较早地在系统中结合了信任这一因素,网站允许用户将他人纳入信任列表或不信任列表,从而获得社会关系。文献[7]提出TidalTrust算法,算法以广度优先的方式,综合考虑了路径长度和信任度大小,通过加权得到节点与节点间的信任度。MoleTrust算法[8]类似于TidalTrust算法,但设定了一个最大路径长度。文献[9]提出TrustWalker的随机游走算法,算法在信任网络中随机遍历用户,综合各个用户的评分数据来预测评分。文献[10]考虑到用户兴趣变化,采用了重启动随机游走算法,能有效提高推荐精度。
一些研究利用信任传播来计算信任度,同时也改善了冷启动和稀疏性问题。文献[11]综合信任传播,通过加权平均来计算信任估计值。文献[12]利用信任传播过程中信任值的衰减,设计了3种计算信任传播的信任度的方法。
一些研究者将信任度和其他因素结合,取代传统CF中的相似度,从而获得更高的推荐精确度。文献[13]将相似度和信任度综合,代替传统CF的相似度,并应用于推荐系统中。文献[14]利用评分-信任协同进行推荐预测,这种混合推荐的技术提高了推荐精度和评分覆盖率。文献[15]提出了结合信任度和社会关系度的电子商务推荐系统,考虑了关于推荐资源的多个因素。
基于信任的推荐算法都在一定程度上改善了数据稀疏性问题,而作为稀疏性的优化方法,近年来,矩阵分解技术在电子商务推荐中应用越来越广泛,文献[16]采用基于随机梯度矩阵分解的社会网络推荐算法,并具有比较好的预测效果。文献[17]在结合社交网络的基础上应用矩阵分解。虽然矩阵分解对于稀疏性问题有较好的效果,但对冷启动问题也无法直接处理,且没有考虑到信任关系在网络中的传播。
近些年针对稀疏性和冷启动问题,基于信任的推荐系统已经有了丰富的研究成果,但也存在一些不足之处。
1) 文献大多只考虑了一个因素,比如信任度,相似度,或两个因素结合,没有综合考虑更多因素,使推荐精度进一步提高。
2) 大多推荐算法需要利用到相似度计算,而相似度计算需要共同评分的项目达到一定数量,而实际上数据是稀疏的,两用户的共同评分项目有时很少甚至没有。
3) 一些基于信任的推荐算法没有意识到信任的朋友有时候并不适合作为邻居用户,因为朋友间也可能会有不同的兴趣偏好,信任用户不一定是相似用户,相似的也不一定是互相信任的,所以需要同时考虑这两个方面。
4) 一些随机游走算法由于要随机遍历整个信任网络,导致整个算法的计算量明显增加,时间复杂度较长。
相比于以前工作的不足,本文综合考虑了信任和相似度,保证随机游走选取的用户既是社交网络中的信任用户,又是兴趣偏好相似的用户,在计算相似度方面采用矩阵分解的方法,避免了共同评分项目过少的情况,在随机游走的的过程中依据信任和相似度的综合权重进行游走,减少了一定的算法复杂度,从而提高了推荐精确度。
1 随机游走推荐算法 1.1 结合信任和相似度的随机游走推荐算法框架结合信任和相似度的随机游走推荐算法分为以下3步。
1) 在已知用户集合、项目集合、评分矩阵的情况下,结合信任度和相似度,通过加权计算出权重TS。
2) 在加权信任网络中,依据权重TS作为随机游走的指标,遍历信任网络中全用户。
3) 终止游走过程,预测目标用户对待评分项目的评分,最终得出推荐。
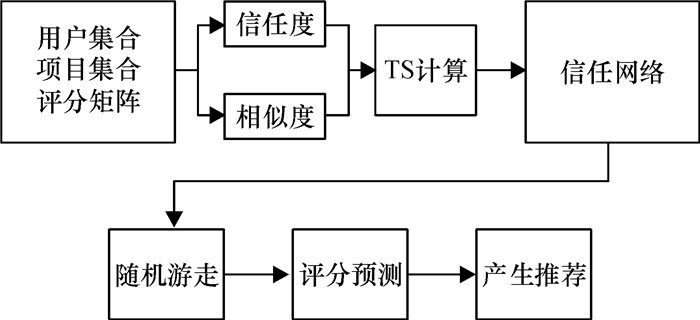
TSWalker算法的流程如图 1所示。
|
图 1 TSWalker算法流程 Fig. 1 The TSWalker algorithm process |
基于信任的推荐算法主要考虑了用户间的信任度,这并不能明显提高推荐的精确度,因为算法选取目标用户的信任用户作为邻居用户,但信任用户与目标可能有不同的偏好,两者兴趣偏好不一致,导致推荐质量下降。结合信任和相似度的随机游走算法在进行游走前,需要计算权重TS,同时考虑了信任度和相似度。
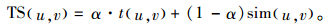
|
其中,sim(u,v)为用户u和用户v之间的相似度;t(u,v)为用户u和用户v之间的信任度。t(u,v)可以从用户的直接评价得出,在本文的实验数据集Epinions上,信任网络为二值信任网络,即用户v在u的信任列表上,信任度为1,不信任则为0。
现阶段计算相似度大多利用协同过滤、杰卡德公式、皮亚诺余项或改进的相似度计算技术,同时用户评分矩阵又很大,导致矢量维度很高,用户评分矩阵稀疏,在此采用一种基于矩阵分解的计算相似度的方法,可以明显提高推荐精确度。对于一个m×n的评分矩阵R,将其降维分解至2个低阶矩阵P和Q。
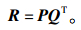
|
其中,P为m×d矩阵;Q为n×d矩阵。将矩阵降维后,采用余弦相似度计算u和v的相似度。
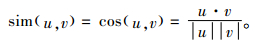
|
从目标用户u0开始进行随机游走,第k步会抵达用户u,如果项目i已被u评分,则停止游走,u对i的评分ru,i即为此步的结果。若u并没有评价i,则:
1) 以概率φu, i, k在u处中止,然后以概率p{Yu=j}从u的评分项目集中选取一个与i相似的项目j,i对j的评分ru,j为此步游走的结果。
u在第k步游走过程中在u处中止的概率φu, k,与i和j的相似度相关,i和j的相似度越高,概率值越大;φu, k的值也与随机游走的深度有关,目标用户u0与用户u之间的游走距离越长,噪音数据也就越多,会严重影响预测的质量,所以φu, k值会随着k值增加。
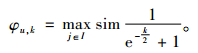
|
其中,sim(i,j)是项目i和项目j之间的相似度,k取值能够保证当k无穷大时,φu, k值接近1,k值比较小时,φu, k值也比较小。现阶段计算项目间相似度值大多依据协同过滤方法,比如皮亚诺余项和一些改进的相似度计算方法,然而当没有用户同时评分过这2个项目时,这些方法就无法计算项目间的相似度了。所以,本文提出一种基于矩阵分解的计算项目之间相似度的方法,同上节,i和j间相似度公式为
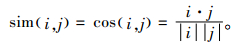
|
当以概率φu, i, k在u处中止时,需要从u的评分项目集中选取项目j, u对j的评分即为此次的结果。u从评分项目集RIu中选取j概率公式为
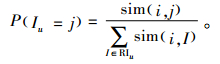
|
2) 以概率1-φu, i, k在网络中继续,从u的直接信任用户集合TUu中选取一个用户v作为第k+1步的用户节点。
一般的随机游走算法选取下一步用户节点是从直接信任用户集合TUu中随机选取,意味着用户u的直接信任用户都有着等同的机率被选取,然后用户的直接信任用户集合中,每个用户都有着自己独特的偏好、习惯、爱好等,与用户u的兴趣偏好相似的直接信任用户被选取的概率应该要大一些,所以,选取用户v的概率为
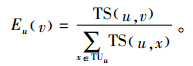
|
其中,TS(u, v)即为上节介绍的权重,TS值越高表明v与u有着越高的信任关系和兴趣偏好相似,可以保证每一步选取的用户都是u直接信任用户集合中与u偏好相似的用户,使评分预测更加精确。
在结合信任与相似度随机游走算法中,u0的预测评分为每步随机游走评分综合。
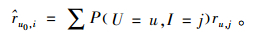
|
P(U=u,I=j)是在用户u处,并选取项目j概率,分为以下3种情况。
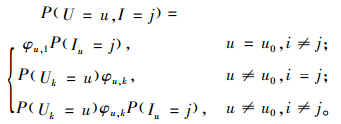
|
其中,Uk=u为选取u为节点;Iu=j为u选取项目j为预测项目。
在第k步,
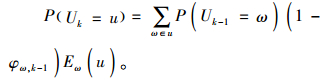
|
根据六度分隔理论,任两个用户可以在不大于6步的情况下获得联系,所以在此限定随机游走最大深度为6步,即当k=6时,随机游走停止。经计算,此公式的最终计算公式为
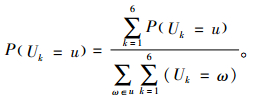
|
每一次随机游走都会返回一个u0对i的预测评分,为了获得更高的推荐效果,会在网络中进行多次随机游走。假设第j次游走的预测评分为rj,i次随机游走的评分平均值为r,当满足如下条件时,算法全部终止。
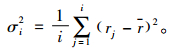
|
其中,σi2是i次随机游走方差。当|σi+12-σi2|≤ε(ε=0.000 1)时,方差收敛,随机游走终止,最终u0对i预测评分为
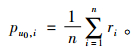
|
其中,ri为每次游走的预测评分;n为游走的总次数。
2 仿真实验 2.1 实验数据集及评价指标选取Epinions数据集进行实验,Epinions数据集开始于1999年,注册会员可以对商品评分,会员之间还可以把别的会员加入自己的信任列表,数据集包括40 163个用户对139 738个商品的评论,有664 824条评分,包括了487 183条信任关系。
评价指标RMSE(均方差误差)通过比较预测值与用户实际评分之间的差异来度量推荐的准确性。
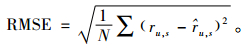
|
Precision(准确率)为系统推荐商品中用户偏好的商品与系统推荐商品总数所占的比例。
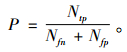
|
其中,Ntp为系统推荐且用户偏好的商品数; Nfp为系统推荐但用户不偏好的商品数;Nfn为系统不推荐但用户偏好的商品数。
Coverage(覆盖率)为系统推荐商品覆盖全部商品的比例。
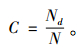
|
F为精确率和覆盖率的调和值。
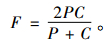
|
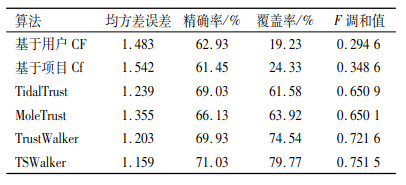
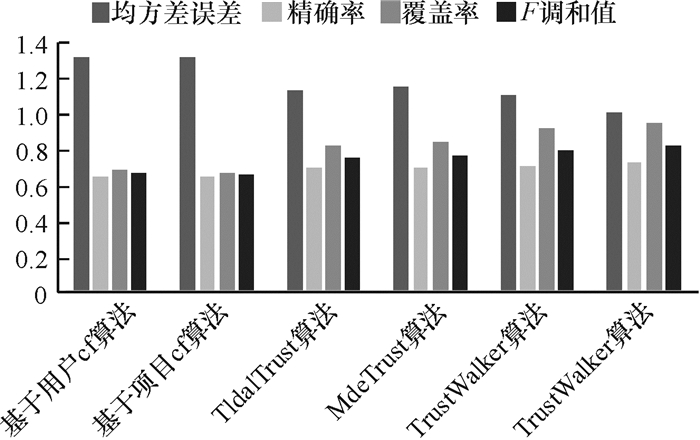
将数据集分为80%训练集与20%测试集,并选取前面提到UserCF、ItemCF、TidalTrust、MoleTrust、TrustWalker算法作为实验参照算法,在计算权重TS时取参数α为0.5。分别对全用户集和冷启动用户集上的实验结果进行推荐质量的对比。在40 163个用户中,认为评分数低于5的即为冷启动用户,共16 910个冷启动用户。表 1和图 2为在全用户集上。
| 表 1 全用户集比较结果 Tab. 1 All User Sets Results |
|
图 2 全用户集比较结果 Fig. 2 All user sets results |
根据表 1和图 2,观察到在全用户集中,推荐算法的精确度在不断提高,越往后的算法考虑的因素越多,所以推荐精度在提高。基于信任的推荐算法相对于CF算法在精确率上并没有很明显优势。CF算法借助用户评分数据计算用户或物品相似度,而基于信任的推荐算法主要考虑的是用户间的信任,没有考虑用户间的兴趣偏好,这可以很明显地提高覆盖率,却不能明显提高精确率。本文提出了权重TS,同时考虑了相似度与信任度,在计算相似度的时候又采用了矩阵分解的方法避免了没有用户同时评分同一商品的情况,通过实验,在均方差误差、精确率、覆盖率、F值等评价指标上均优于其他算法。
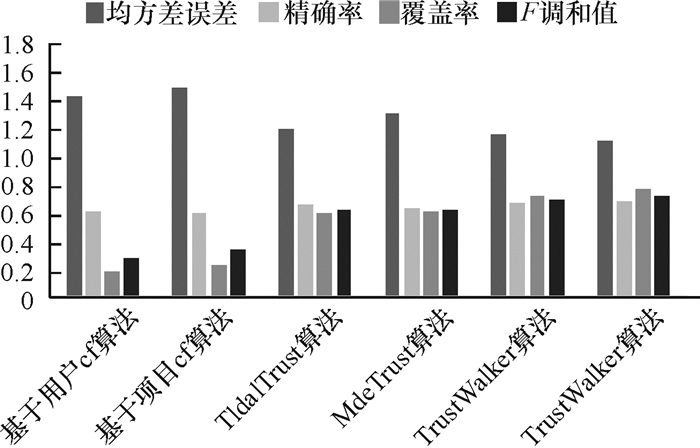
根据实验结果,结合信任和相似度的随机游走算法在冷启动用户集中具有较好的推荐效果。传统的协同过滤算法推荐质量最差,因为在冷启动用户集中,很少有商品被两个及以上用户评分过,意味着用户或物品相似度很难计算,从而降低推荐质量。在推荐算法中引进信任网络,能够明显提高覆盖率,但在冷启动用户集中精确率仍提升不明显。TrustWalker算法和TSWalker算法在精确率和覆盖率上均有优势,相比下TSWalker算法有更高的推荐精度,TSWalker算法同时考虑了信任度和相似度,并将TS权重应用于随机游走算法,具有很好推荐效果。如表 2、图 3所示。
| 表 2 冷启动用户集比较结果 Tab. 2 Cold start user sets results |
|
图 3 冷启动用户集比较结果 Fig. 3 Cold start user sets results |
由于评分数据集非常大,需考虑推荐算法时间复杂度,图 4为各种算法复杂度平均值。可以观察到协同过滤算法耗费时间最短,因为协同过滤算法仅主要考虑用户的评分数据,相反,其他算法需要考虑到信任度,从而提高了算法计算量。相比于其他随机游走算法,TSWalker算法的时间复杂度要低一些,主要因为算法在随机游走的每一步中,都会依据TS权重选取目标用户,而不是随机选取,从而可以提高计算效率。

|
图 4 各算法时间复杂度对比结果 Fig. 4 Time costs of different algorithms |
考虑推荐算法的稀疏性和冷启动等问题,结合信任度和相似度,使随机游走算法下一步选取的用户既是社交网络中的信任用户,又是兴趣偏好相似的用户,在计算相似度上利用了矩阵分解的方法,防止了传统算法中共同评分项目过少的局限,并依据综合权重TS进行随机游走,提高了推荐质量。
今后会考虑2个角度。一是本文的信任度直接利用数据集上的信任度,需要考虑到信任的变化,在信任网络中通过信任传播等方式计算信任度。二是在电子商务网站上需要考虑到推荐算法的实时性,能够及时为用户推荐真正需要的商品是推荐系统的目的。
| [1] |
TAO Z, JIE R, MAT AÚU1 S M, et al. Bipartite network projection and personal recommendation[J].
Physical Review E, 2007, 76(4): 70-80.
|
| [2] |
KANG G, LIU J, TANG M, et al. AWSR: active web service recommendation based on usage history[C]. Proceedings of the 19th International Conference on Web Services. IEEE, 2012:186-193.
|
| [3] |
谭学清, 黄翠翠, 罗琳. 社会化网络中信任推荐研究综述[J].
现代图书情报技术, 2014, 30(11): 10-16.
DOI: 10.11925/infotech.1003-3513.2014.11.02. |
| [4] |
SU X, KHOSHGOFTAAR T M. A survey of collaborative filtering techniques[J].
Advances in Artificial Intelligence, 2009(12): 1-19.
|
| [5] |
NILASHI M, IBRAHIM O B, ITHNIN N. Hybrid recommendation approaches for multi-criteria collaborative filtering[J].
Expert Systems with Applications, 2014, 41(8): 3879-3900.
DOI: 10.1016/j.eswa.2013.12.023. |
| [6] |
MASSA P, AVESANI P.Trust metrics in recommender systems[M].Computing with Social Trust. Berlin: Springer, 2009:259-285.
|
| [7] |
GOLBECK J A. Computing and applying trust in web-based social networks[D].USA:University of Maryland, 2005.
|
| [8] |
MASSA P, AVESANI P. Trust Metrics on controversial users: balancing between tyranny of the majority[J].
International Journal on Semantic Web & Information Systems, 2007, 3(1): 39-64.
|
| [9] |
JAMALI M, ESTER M. TrustWalker:a random walk model for combining trust-based and item-based recommendation[C]//Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2009:397-406.
|
| [10] |
俞琰, 邱广华. 用户兴趣变化感知的重启动随机游走推荐算法研究[J].
现代图书情报技术, 2012(4): 48-53.
YU Yan, QIU Guanghua. Research on user interest shift aware random walk with restart recommendation algorithm[J]. New Technology, 2012(4): 48-53. DOI: 10.11925/infotech.1003-3513.2012.04.08. |
| [11] |
韩丽. 社交网络中的信任推荐和好友搜索过滤算法研究[D]. 秦皇岛: 燕山大学, 2012.
HAN Li.Research on recommendation and search filter of friends algorithm in social networks[D].Qinhuangdao:Yanshan University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10216-1012025582.htm |
| [12] |
CHAKRABORTY P S, KARFORM S. Designing trust propagation algorithms based on simple multiplicative strategy for social networks[J].
Procedia Technology, 2012, 6(6): 534-539.
|
| [13] |
陈晓城. 基于信任传播模型的协同过滤推荐算法研究[D]. 广州: 中山大学, 2010.
CHEN Xiaocheng.Research of collaborative filtering recommendation algorithm based on trust propagation model[D].Guangzhou: Zhongshan University, 2010. |
| [14] |
秦继伟, 郑庆华, 郑德立, 等. 结合评分和信任的协同推荐算法[J].
西安交通大学学报, 2013, 47(4): 100-104.
QIN Jiwei, ZHENG Qinghua, ZHENG Deli, et al. A collaborative recommendation algorithm based on ratings and trust[J]. Journal of Xi'an Jiaotong University, 2013, 47(4): 100-104. |
| [15] |
Li Y M, Wu C T, Lai C Y. A social recommender mechanism for e-commerce: Combining similarity, trust, and relationship[J].
Decision Support Systems, 2013, 3(3): 740-752.
|
| [16] |
李卫平, 杨杰. 基于随机梯度矩阵分解的社会网络推荐算法[J].
计算机应用研究, 2014, 31(6): 1654-1656.
LI Weiping, YANG Jie. Stochastic gradient matrix factorization based on social network recommender algorithm[J]. Application Research of Computers, 2014, 31(6): 1654-1656. |
| [17] |
MA H, KING I, LYU M R.Learning to recommend with social trust ensemble[C]//Proceedings of the 32nd International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2009:203-210.
|
 2016, Vol. 19
2016, Vol. 19