2. 朝阳科技大学 管理学院,台湾 台中 10617
2. College of Management, Chaoyang University of Technology, Taichung 10617, China
商业信用交易越来越成为供应链上下游企业间交易的主要方式,是一种灵活的供应链内部短期融资策略[1]。卖方向买方提供商业信用交易可以得到两大好处:1)买方把它当作一种现金折扣,从而促进销售[2];2)作为直接现金折扣的代替,不容易引起竞争对手的降价竞争[3]。但是另一方面,向买方提供商业信用期,也会给卖方带来增加机会成本和面临着违约风险的问题。因此,如何确定一个最优的信用期,使得信用期带来的收入增加明显盖过由机会成本和违约风险带来的成本增加,是一个需要卖方决策的重要问题。大多数基于商业信用批量模型的研究都是把信用期当作给定参数而不是决策变量,如文献[4-7],而把信用期当做决策变量的研究又存在这样或那样的缺陷。文献[8-10]利用差分方程把信用期作为决策变量引入目标函数,但没有考虑信用期带来的机会成本和违约风险问题;文献[11-13]忽略了机会成本;文献[3, 14]考虑了信用期带来的机会成本和违约风险,但其假设需求仅与信用期有关而与价格无关;文献[15-18]从供应链的角度研究了信用期的优化问题,但是它们的共同问题是假设不存在违约风险。
本文在EPQ(economic production quantity,经济生产批量)架构下,探讨卖方的信用期和批量优化问题,与其他研究不同之处以及亮点在于:1)把卖方定位为一个制造商,其生产系统是非完美生产系统,即存在一定的次品率,而且制造商生产过程中存在明显的学习曲线效应,即随着产量的增加边际生产成本下降;2)不仅考虑信用期给制造商带来的扩大需求的好处,而且综合考虑信用期带来的机会成本和违约风险;3)定义一种更符合实际情况的需求函数,即需求同时受信用期和销售价格的影响。
1 模型假设与参数说明1) 制造商的生产系统非完美,即生产过程中会产生一定比例的残次品,次品率为λ,单位残次品损失成本为g。
2) 制造商向下游采购商提供商业信用交易,商业信用期为M。
3) 制造商生产过程中存在典型的学习效应。借用Arrow[19]提到的经典生产学习曲线模型:假设v(t)为t时刻单位产品的生产成本,X(t)为t时刻累积产品产量,v0为生产首件产品的学习曲线生产成本,u为学习能力系数,u值越小学习能力越强,当u=1,表示没有学习能力,一般取值范围为0.5≤u≤0.9,t时刻累计生产成本为v(t)X(t)=v0[X(t)]u。
4) 需求速度D同时受销售价格s和信用期M的影响。根据销售价格越低需求越高,信用期越长需求越高的市场逻辑,令
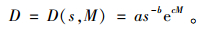
|
其中,a、b、c均为正的常数,a为市场刚需系数; b为需求的价格影响系数; c为需求的信用期影响系数。
5) 制造商的生产速度为P,P > D+λ,生产批量为Q,边生产边对产成品进行残次品检测,生产完成时对检测出的残次品进行一次性库存移除。
6) 考虑下游采购商违约的风险,假设采购商违约的概率F是信用期M的函数,且有
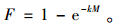
|
其中, k为违约风险系数,是正的常数,k值越大,同等信用期下违约的概率越高。
7) 基于信用期带来的收入延迟存在货币时间价值损失,考虑净收入的现值问题。假设年综合利率为r,则制造商单位时间的净收入现值为
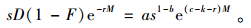
|
8) 制造商一次生产准备成本为A,单位产品单位时间的存货持有成本为h。
9) 不允许缺货。
2 模型构建和优化求解 2.1 制造商利润函数制造商周期内库存变化情况如图 1所示。制造商的成本项目包括生产成本、残次品损失成本、生产准备成本和存货持有成本。根据假设3),基于学习曲线的单位时间生产成本为
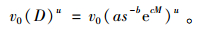
|
单位时间残次品损失成本为
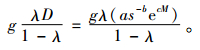
|
单位时间生产准备成本为
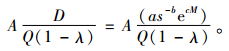
|
单位时间存货持有成本为

|
设制造商的利润函数为Π(Q, M),则有
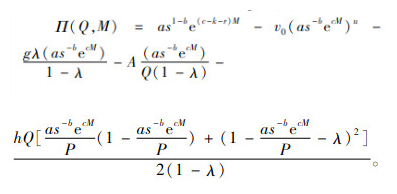
|
(1) |
在制造商的利润函数(1)中,后两项与生产批量Q相关,令
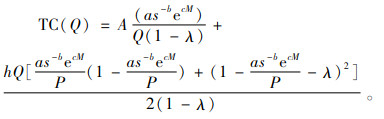
|
(2) |
这里利用算术平均值-几何平均值不等式来求Q的最优解。根据算术平均值-几何平均值不等法则,不等式
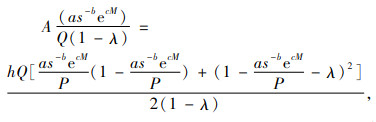
|
(3) |
求得制造商最佳生产批量为
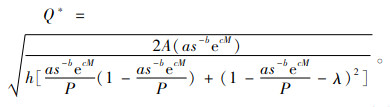
|
(4) |
此时,对应的最小成本为
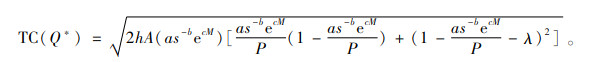
|
(5) |
把式(5)代入式(1),式(1)简化为单决策变量M的函数,如下所示:
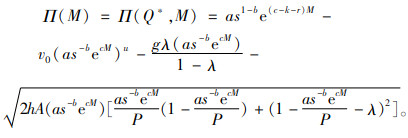
|
(6) |
对式(6)针对M求一阶导数并令其导数为零,有
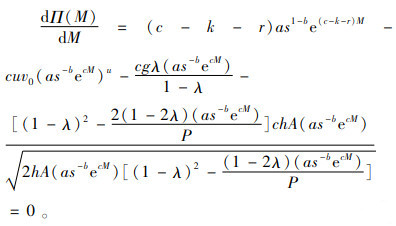
|
(7) |
从式(7)可以推导出以下结论。
定理1:如果c≤k+r且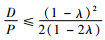
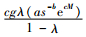
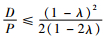
证明:当满足c≤k+r且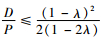
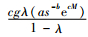
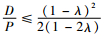
易得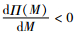
定理1符合以下简单的经济学解释。
1) 当c≤k+r时,制造商给予下游购买商的信用期越长(即M值越大),其净收入现值(即[(c-k-r)as1-be(c-k-r)M])越小,因此制造商不会向下游购买商提供商业信用。
2) 当制造商的边际净收入增长(即[(c-k-r)as1-be(c-k-r)M])低于或等于非完美生产系统的边际生产成本(即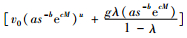
需要注意的是,以上结论均在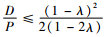
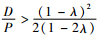
下面进一步探讨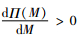
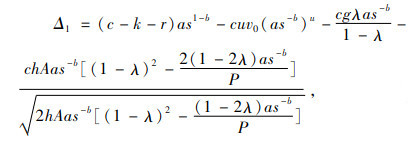
|
(8) |
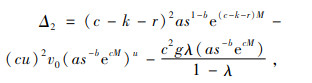
|
(9) |
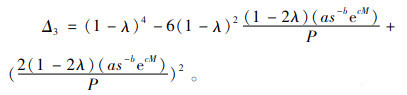
|
(10) |
定理2:1)如果Δ1>0,Δ2≤0且Δ3 > 0,则存在唯一的最优信用期M* > 0,使得制造商的利润最高;
2) 如果Δ1≤0,Δ2≤0且Δ3>0,则制造商取消商业信用(M*=0)时利润最高。
证明:对式(6)针对M求二阶导数,
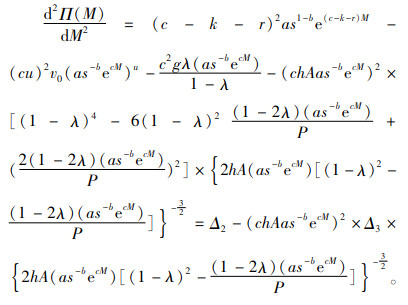
|
(11) |
当Δ2≤0且Δ3>0时,根据式(11)易得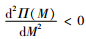
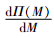
因为
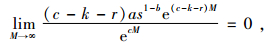
|
所以有
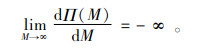
|
(12) |
把M=0代入式(7),得到
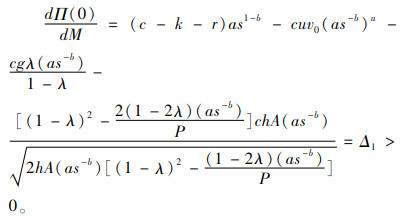
|
(13) |
根据中值定理,一定存在唯一的M*>0使得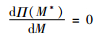
当Δ1≤0时,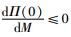
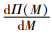
下面通过算例和灵敏度分析来进一步验证模型的可行性和合理性,同时通过灵敏度分析将得到一些有益的结论。算例和灵敏度分析将依赖于以下的参数设置:
市场刚需系数a=1 000, 需求的信用期影响系数c=0.2,需求的价格影响系数b=0.1,违约风险系数k=0.1,综合年利率r=0.05,学习能力系数u=0.9,次品率λ=0.05,单位残次品的损失成本g=5,首件产品生产成本v0=8,销售单价s=18,一次生产准备成本A=50,单位货物单位时间的存货持有成本h=2, 生产速度P=10 000。
3.1 算例分析先把以上参数代入式(8),算得Δ1=45.75>0;接着把以上参数代入式(7),得到一个只包含单变量M的方程,利用Matlab软件求得M*=0.56。把M*=0.56代入式(9)和(10)进行验证,得到Δ2=-84.91、Δ3=0.43。根据定理2,M*=0.56是最优解。把M*=0.56代入式(4),算得Q*=225.01;最后把M*=0.56和Q*=225.01代入式(1),得Π(Q*, M*)=10 111.71。
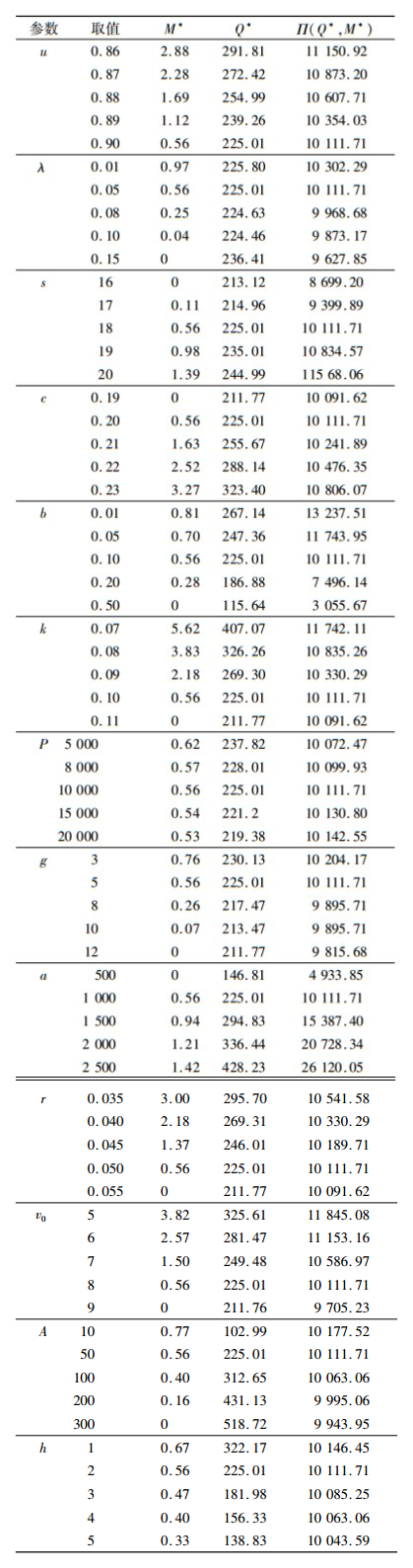
3.2 灵敏度分析在其他参数值固定不变时,变化某一参数进行该参数的灵敏度分析,计算结果如表 1所示。
| 表 1 参数的灵敏度分析 Tab. 1 The sensitive analysis of parameters |
由表 1可知,在其他条件不变的情况下有如下结果。
1) 随着制造商生产过程中学习能力的增强,即u值变小,给予下游购买商的信用期增长,生产批量增大,企业利润增加。
2) 随着制造商生产过程中次品率的增加,即λ值变大,给予下游购买商的信用期变短(甚至为0),生产批量先变小后变大,企业利润减少。
3) 随着制造商销售价格的降低,即s值变小,给予下游购买商的信用期变短(甚至为0),生产批量变小,企业利润减少。
4) 需求对信用期越不敏感,即c值变小,给予下游购买商的信用期越短(甚至为0),生产批量越小,企业利润越低。
5) 需求对价格越不敏感,即b值越大(因为需求函数中参数b前面带有负号),给予下游购买商的信用期越短(甚至为0),生产批量越小,企业利润越低;
6) 下游购买商违约风险越高,即k值越大,给予下游购买商的信用期越短(甚至为0),生产批量越小,企业利润越低。
7) 制造商生产速度越快,即P值越大,给予下游购买商的信用期越短,生产批量越小,企业利润越高。
8) 随着单位残次品损失成本的增加,即g值变大,给予下游购买商的信用期变短(甚至为0),生产批量变小,企业利润减少。
9) 随着市场刚需的减少,即a值变小,给予下游购买商的信用期变短(甚至为0),生产批量变小,企业利润减少。
10)随着年复合利率的增加,即r值变大,给予下游购买商的信用期变短(甚至为0),生产批量变小,企业利润减少。
11)随着制造商首件产品生产成本的增加,即v0值变大,给予下游购买商的信用期变短(甚至为0),生产批量变小,企业利润减少。
12)随着制造商生产准备成本的增加,即A值变大,给予下游购买商的信用期变短(甚至为0),生产批量变大,企业利润减少。
13)随着制造商单位产品单位时间持有成本的增加,即h值变大,给予下游购买商的信用期变短,生产批量变小,企业利润减少。
4 结论单纯从卖方视角研究信用期优化的研究很少,本文把卖方定位为生产过程中存在学习效应的非完美生产制造商,假设需求同时受信用期和销售价格的影响,信用期给制造商带来机会成本和违约风险成本,较好地反映了现实情况。站在制造商的视角构建了制造商的信用期和生产批量优化模型,并通过定理证明了在一定条件下,模型存在唯一的最优解。在构建模型的基础上,用算例验证了模型的可行性和合理性,并通过对13个参数进行灵敏度分析,得出了一系列在参数变化情况下的决策性结论。
进一步深化研究,本文可以从以下多方面进行扩展:比如可以把产品假设为易腐品,加入变质率参数;考虑双重学习效应,即生产过程中不仅边际生产成本随着产量的增加而降低,而且次品率也随着产量的增加而降低;考虑次品的再制造等。
| [1] |
STOKES J R. Dynamic cash discounts when sales volume is stochastic[J].
The Quarterly Review of Economics and Finance, 2005, 45(1): 144-160.
DOI: 10.1016/j.qref.2004.08.001. |
| [2] |
ARCELUS F J, SHAH N H, SRINIVASAN G. Retailer′s response to special sales: price discount vs. trade credit[J].
Omega, 2001, 29(5): 417-428.
DOI: 10.1016/S0305-0483(01)00035-4. |
| [3] |
LOU K R, WANG W C. Optimal trade credit and order quantity when trade credit impacts on both demand rate and default risk[J].
Journal of the Operational Research Society, 2012, 64(10): 1551-1556.
|
| [4] |
MIN J, ZHOU Y W, ZHAO J. An inventory model for deteriorating items under stock-dependent demand and two-level trade credit[J].
Applied Mathematical Modelling, 2010, 34(11): 3273-3285.
DOI: 10.1016/j.apm.2010.02.019. |
| [5] |
MAHATA G C. An EPQ-based inventory model for exponentially deteriorating items under retailer partial trade credit policy in supply chain[J].
Expert systems with Applications, 2012, 39(3): 3537-3550.
DOI: 10.1016/j.eswa.2011.09.044. |
| [6] |
CHEN S C, TENG J T, SKOURI K. Economic production quantity models for deteriorating items with up-stream full trade credit and down-stream partial trade credit[J].
International Journal of Production Economics, 2014(155): 302-309.
|
| [7] |
SONI H N, PATEL K A. Optimal strategy for an integrated inventory system involving variable production and defective items under retailer partial trade credit policy[J].
Decision Support Systems, 2012, 54(1): 235-247.
DOI: 10.1016/j.dss.2012.05.009. |
| [8] |
THANGAM A, UTHAYAKUAMR R. Two-echelon trade credit financing for perishable items in a supply chain when demand depends on both selling price and credit period[J].
Computers & Industrial Engineering, 2009, 57(3): 773-786.
|
| [9] |
CHEN L H, KANG F S. Integrated inventory models considering the two-level trade credit policy and a price-negotiation scheme[J].
European Journal of Operational Research, 2010, 205(1): 47-58.
DOI: 10.1016/j.ejor.2009.11.028. |
| [10] |
GUCHHAIT P, MAITI M K, MAITI M. An EOQ model of deteriorating item in imprecise environment with dynamic deterioration and credit linked demand[J].
Applied Mathematical Modelling, 2015, 39(11): 6553-6567.
|
| [11] |
ZHOU Y W, ZHONG Y, LI J. An uncooperative order model for items with trade credit, inventory-dependent demand and limited displayed-shelf space[J].
European Journal of Operational Research, 2012, 223(1): 76-85.
DOI: 10.1016/j.ejor.2012.06.012. |
| [12] |
WANG W C, TENG J T, LOU K R. Seller's optimal credit period and cycle time in a supply chain for deteriorating items with maximum lifetime[J].
European Journal of Operational Research, 2014, 232(2): 315-321.
DOI: 10.1016/j.ejor.2013.06.027. |
| [13] |
ZHONG Y G, ZHOU Y W. The model and algorithm for determining optimal ordering/trade-credit policy of supply chains[J].
Applied Mathematics and Computation, 2012, 219(8): 3809-3825.
DOI: 10.1016/j.amc.2012.10.009. |
| [14] |
CHERN M S, PAN Q, TENG J T, et al. Stackelberg solution in a vendor-buyer supply chain model with permissible delay in payments[J].
International Journal of Production Economics, 2013, 144(1): 397-404.
DOI: 10.1016/j.ijpe.2013.03.008. |
| [15] |
TENG J T, LOU K R. Seller's optimal credit period and replenishment time in a supply chain with up-stream and down-stream trade credits[J].
Journal of Global Optimization, 2012, 53(3): 417-430.
DOI: 10.1007/s10898-011-9720-3. |
| [16] |
LUO J, ZHANG Q. Trade credit: a new mechanism to coordinate supply chain[J].
Operations Research Letters, 2012, 40(5): 378-384.
DOI: 10.1016/j.orl.2012.04.008. |
| [17] |
汤勤深, 周永务, 郑倩倩. 变化信用期下易变质品分散独立决策供应链系统[J].
工业工程, 2013, 16(3): 38-44.
TANG Qinshen, ZHOU Yongwu, ZHENG Qianqian. A decentralized supply chain system for deteriorating items with credit-linked demand and varying credit period[J]. Industrial Engineering Journal, 2013, 16(3): 38-44. |
| [18] |
ZHANG Q H, DONG M, LUO J, et al. Supply chain coordination with trade credit and quantity discount incorporating default risk[J].
International Journal of Production Economics, 2014, 153: 352-360.
DOI: 10.1016/j.ijpe.2014.03.019. |
| [19] |
ARROW K J. The economic implications of learning by doing[J].
The Review of Economic Studies, 1962, 29(3): 155-173.
DOI: 10.2307/2295952. |
 2016, Vol. 19
2016, Vol. 19