随着气候不断变暖,低碳经济的快速发展,减少CO2的排放、减缓全球气候变暖已经成为全世界各国的共识。在当前全球经济发展与社会经济发展的态势下,构建绿色供应链是企业实现可持续发展不可置疑的必然选择[1]。与一般供应链网络优化问题相比,绿色供应链网络优化问题不仅考虑经济效益最优,同时还考虑环境最优和社会效益最优[2]。
为了降低温室气体给环境带来的负面影响,实现我国以环境友好型和资源节约型为目标的可持续发展战略,低碳供应链有效地将环保思维融入到所有物流和供应链环节中,实现最小碳排放的绿色供应链体系。近年来,关于低碳供应链网络问题被广泛研究。吕品[3]研究了多个厂商、多个配送中心和多个客户情况下的三层供应链网络,提出了考虑碳排放成本的供应链网络设计模型。沈连梅等[4]针对确定需求闭环物流网络中工厂与配送中心的两级选址问题,考虑最优客户满意度及网络低碳。Kannan等[5]利用碳足迹的方法考虑了在确定型逆向供应链中的企业节点选址问题。Yang等[6]在碳税限制条件下,建立了一个双线性非凸集混合整数规划模型,得到了满足低碳限制的新的供应链网络。Zhang等[7]通过路径和运输方式的改变可以实现低碳限制的目标,并得到低碳限制与系统运输时间以及网络碳排量之间的关系。高举红等[8]考虑碳排放和市场不确定,针对多层级多产品的家电闭环供应链网络设计建立了规划模型。杨建华等[9]针对碳税政策对城市冷链物流配送的成本压力,建立了一个考虑碳税成本、冷库能力受限的网络模型。
闭环供应链网络涉及供应商、制造工厂、配送中心、回收中心、处置中心、消费者等多种有效组织。同时,由于供应链上各设施的数量、位置、能力等因素的限制,使得整个网络在设计与优化方面困难重重。伍星华等[10]以再制造闭环物流网络设计为研究对象,考虑设施的规模选择和正逆向物流的集成运作,建立了一个多周期优化设计模型。涂南等[11]提出了一个考虑设施扩展的多周期、多产品、多级的闭环物流网络模型。孙浩等[12]构建了一个制造/再制造集成物流网络,考虑固定费用节省率、最小回收率和政府补贴等因素建立混合整数非线性规划模型。El-sayed等[13]建立了包含正向与逆向物流网络的多周期多阶段随机整数线性规划模型,来决策设施的位置、运输路线及设施间的产品流量,实现供应链的最大利润。Pishwaee等[14]利用鲁棒优化方法对运输价格、需求量和回收量不确定的闭环供应链网络规划问题进行研究,并证明模型的有效性。同时,在闭环供应链网络研究中,除了上述所考虑因素外,企业要想在如今这个竞争激烈的社会中生存,需要站在消费者的角度去思考问题。Fenies等[15]认为客户服务水平是供应链设计的重要目标之一。因此,为了提高供应链绩效,考虑提高消费者的服务水平是必不可少的。
本文在低碳经济背景下,针对单一产品研究具有多个供应商、多个制造商、多个消费者、多个配送中心、多个回收中心以及多个处理中心的多层级闭环供应链网络。考虑网络设施建设方式、低碳、顾客服务等因素,以网络运营成本、碳排放成本和顾客需求响应时间成本为目标建立规划模型来研究企业网络布局问题。通过分析所得结果能有效解决物流网络内各设施选址建设、运输量等网络资源配置问题,为企业供应链网络设计提供服务支持。
1 模型构建 1.1 问题描述与模型假设本文考虑一个多目标多层级的闭环供应链网络(如图 1),包括供应商、制造工厂、配送中心、回收中心、废品处理中心及销售区。在网络中,供应商提供原材料通过制造工厂生产出消费者所需产品,随后将产品运往配送中心,配送中心再将产品送到消费者手中,以满足各消费者的需求。回收中心从消费者处将废旧产品的回收并分类处理,根据回收产品情况分别送到制造工厂再加工或废品处理中心进行处理。其中,制造工厂、配送中心、回收中心和废品处理中心等设施的设置数量和处理能力均具有一定限制。本文在考虑这些约束的情况下,以网络运营成本、碳排放成本和顾客需求响应时间成本为目标建立规划模型,对网络中设施建设、选址等网络资源配置问题进行优化。

|
图 1 闭环供应链网络 Fig. 1 Closed-loop supply chain network |
为方便模型构建,作出如下假设。
1) 供应商规模和销售区需求确定且已知。
2) 在备选地点考虑制造工厂、回收中心、配送中心和废品处理中心的选址。
3) 只考虑产品在运输过程中的碳排放量,不考虑各种设施开设和运营时产生的碳排放,运输过程中产生的碳排放量与运输量有关。
4) 忽略回收过程中产品的损耗,即经回收中心检测合格的废旧产品全部被再处理,不合格的全部被销毁。
5) 设施建设成本与处理能力由备选地点建设方式决定,单位建设成本固定不变;设施之间的运输成本由设施之间的距离决定,单位运输成本固定不变。
2.2 符号说明1) 集合变量。
I为原材料种类集合,i=1, 2, …, I;
J为产品种类集合,j=1, 2, …, J;
V为供应商集合,v=1, 2, …, V;
M为备选制造工厂集合,m=1, 2, …, M;
C为销售区集合,c=1, 2, …, C;
R为备选回收中心集合,r=1, 2, …, R;
P为备选配送中心集合,p=1, 2, …, P;
L为备选废品处理中心集合,l=1, 2, …, L;
N为备选地点建设方式集合,n=1, 2, …, N。
2) 模型参数。
Dcj为消费者c对产品j的需求量;
fkn为第n种建设方式下,设施k的建设成本,其中k∈M∪C∪R∪P。
Cvi为供应商v购买原材料i的单位采购成本;
Cmj为制造工厂m生产产品j的单位生产成本;
Cp为配送中心p对产品的单位运作成本;
Cr为回收中心r对回收产品的单位回收成本;
Cmj为制造工厂m修复回收产品j的单位修复成本;
Cl为废品处理中心l处理废品的单位处理成本;
dvmi为原材料i从供应商v到制造工厂m的运输距离;
dmpj为产品j从制造工厂m到配送中心p的运输距离;
dpcj为产品j从配送中心p到消费者c的运输距离;
dcrj为回收产品j从消费者c到回收中心r的运输距离;
drmj为再处理产品j从回收中心r到制造工厂m的运输距离;
drlj为废品j从回收中心r到废品处理中心l的运输距离;
CAvi为供应商v提供原材料i的能力;
CAmn为第n种建设方式下制造工厂m的处理能力;
CApn为第n种建设方式下配送中心p的处理能力;
CArn为第n种建设方式下回收中心r的处理能力;
CAmn为第n种建设方式下制造工厂m的修复能力;
CAln为第n种建设方式下废品处理中心l的处理能力;
M′为制造工厂数量最大限制;
P′为配送中心数量最大限制;
R′为回收中心数量最大限制;
L′为废品处理中心数量最大限制。
3) 其他参数设置。
tpc为从配送中心p到消费者c的产品传递时间;
tcr为从销售区c到回收中心r的产品传递时间;
Ea为配送中心p到销售区c的产品供给的预期时间;
Eb为销售区c到回收中心r的产品回收的预期时间;
α为销售区的产品供给延迟单位时间成本;
β为销售区的产品回收延迟单位时间成本;
δ为原材料/产品单位运输成本;
Q为单位原材料/产品单位运输距离产生的碳排放量;
ω为碳排放税率;
τij为产品j对原材料i的利用率;
γjm为产品j对制造工厂m处理能力的利用率;
θ为产品的回收率;
ρ为回收产品的维修率,1-ρ为回收产品的处理率。
4)决策变量。
Svmi为原材料i从供应商v到制造工厂m的运量;
Suwj为产品j从地点u到地点w的运量,其中(u, w)=M×P∪P×C∪C×R∪R×M∪R×L;
Xmn为0-1变量,在m处建立第n种方式的制造工厂为1,否则为0;
Ypn为0-1变量,在p处建立第n种方式的配送中心为1,否则为0;
Zrn为0-1变量,在r处建立第n种方式的回收中心为1,否则为0;
Uln为0-1变量,在l处建立第n种方式的废品处理中心为1,否则为0。
1.3 目标函数
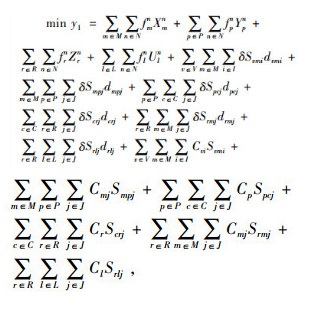
|
(1) |
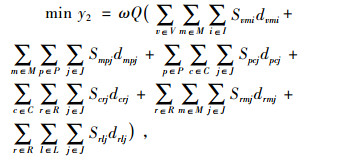
|
(2) |
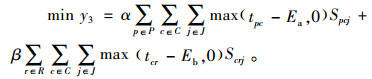
|
(3) |
目标函数(1)表示网络中运营成本,包括各设施建设成本、产品/原材料的运输成本及相关运作费用。目标函数(2)表示网络中碳排放成本,包括各设施之间因运输产生的碳排放量与碳税税率的乘积。目标函数(3)表示需求时间响应成本,指配送中心到消费者的配送延迟成本与消费者到回收中心的回收延迟成本。
1.4 约束条件
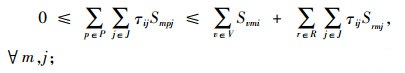
|
(4) |
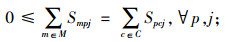
|
(5) |
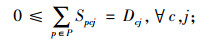
|
(6) |
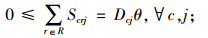
|
(7) |
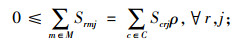
|
(8) |
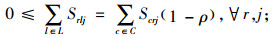
|
(9) |
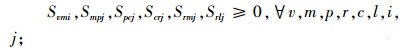
|
(10) |
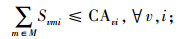
|
(11) |
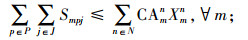
|
(12) |
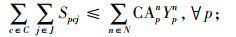
|
(13) |
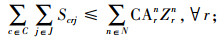
|
(14) |
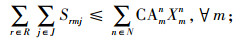
|
(15) |
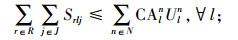
|
(16) |
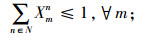
|
(17) |
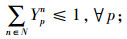
|
(18) |
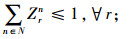
|
(19) |
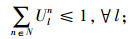
|
(20) |
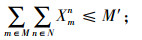
|
(21) |
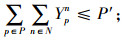
|
(22) |
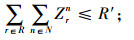
|
(23) |
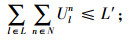
|
(24) |
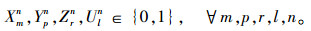
|
(25) |
其中,约束(4)确保从制造工厂运出数量不大于供应商和回收中心运入的数量;约束(5)确保进入配送中心的数量等于输出配送中心的数量;约束(6)确保销售区的需求得到满足;约束(7)确保从销售区回收的产品数量等于进入回收中心的数量;约束(8)确保从回收中心到制造工厂再处理产品的数量等于进入回收中心产品的数量与修复率的乘积;约束(9)确保从回收中心到处理中心的废弃品数量等于进入回收中心产品数量与处理率的乘积;约束(10)保证所有决策变量的非负性。约束(11)确保供应商到制造工厂原材料数量不大于该供应商的供给能力;约束(12)~(16)确保到制造工厂、配送中心、回收中心、废品处理中心的相关产品/零部件不得超出其处理能力。约束(17)~(20)确保制造工厂、配送中心、回收中心和废弃品处理中心最多只有一种建设方式;约束(21)~(24)对制造工厂、配送中心、回收中心和废弃品处理中心设置数量的限制;约束(25)保证决策变量的二元性。
1.5 模型求解Pareto最优解是目前求解多目标优化问题最常用的方法,但是其本质还是根据决策者的喜好以单个目标为主导进行决策,无法很好地反映单个目标最优解与多目标满意解之间的关系[16]。而模糊优化求解多目标问题能较好地考虑不同性质、相互矛盾的多个目标的满意程度,使各个目标都尽可能处于较优状态[17]。本文将采用模糊优化方法进行求解。分别计算总运营成本、碳排放成本和顾客需求响应时间成本的模糊隶属度。由于3个目标函数均是求最小值,故其模糊隶属度计算方法如下。
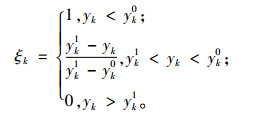
|
其中,yk为目标函数值,yk0和yk1分别为单目标函数的理想值和最差值。然后将3个目标函数分别与约束条件单独进行求解,求出各个目标函数的理想值和最差值,从而求得ξk。最后,将多目标函数转化为单目标函数:min y=λ1ξ1+λ2ξ2+λ3ξ3。λ1、λ2和λ3分别为多目标模糊隶属度的权重。
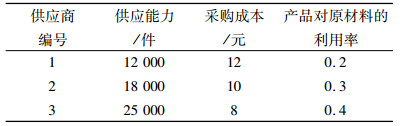
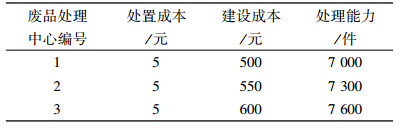
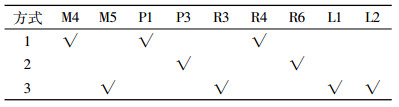
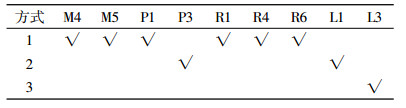
2 算例 2.1 算例描述本文以Y公司的某种产品为例,根据S地区相关情况构建一个多层级闭环供应链网络,该网络中包括3个供应商、5个制造工厂、6个回收中心、4个配送中心、3个处理中心和6个销售区,且每个备选设施建设方式均有高、中、低3种类型。其中,每个供应商只提供一种类型的原材料,最终生成一种产品。相关参数数据见表 1~表 7。
| 表 1 供应商相关参数 Tab. 1 Parameters of supplier |
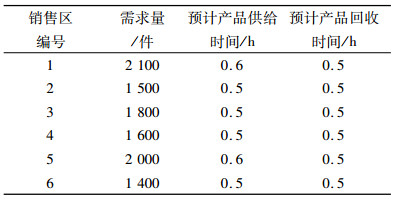
| 表 2 销售区相关参数 Tab. 2 Parameters of customer |
| 表 3 制造工厂相关参数 Tab. 3 Parameters of manufacture |
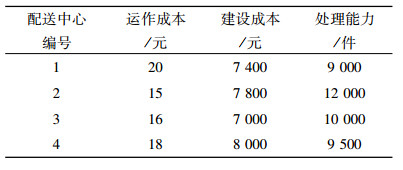
| 表 4 配送中心相关参数 Tab. 4 Parameters of deliver center |
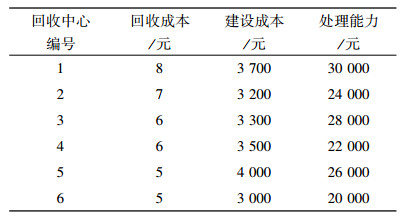
| 表 5 回收中心相关参数 Tab. 5 Parameters of recovery center |
| 表 6 废品处理中心相关参数 Tab. 6 Parameters of dispose center |
| 表 7 其他参数设定 Tab. 7 Other parameters |
假设初始情况下,S地区备选网络设施的能力相同,且各目标模糊隶属度的权重均相等,通过Lingo11.0求解得到目标函数y=2 019 019,各设施选址与建设方式见表 8。可以看出,在网络设施建设成本与生产能力相同的情况下,设施在建设时会优先选择较高级别的方式进行建设,以此来提高设施的能力。由于S地区有关城市的经济、人文等因素的影响,使得备选设施建设成本与生产能力不同,因此当设施初始成本与能力不同时,通过Lingo11.0求解所得y=2 105 365,且选址方案见表 9。可以看出,以节约成本为目的,在设施能力不同时,综合考虑环境、运距、消费者等相关因素,各设施的建设会更倾向于选择成本与能力较低的级别,且设施间的流量会随着建设方式的选择而变化。由此可见,设施能力的不同对网络总成本影响较小,但对网络设施建设方式选择影响较大。
| 表 8 网络设施能力相同下的建设方式 Tab. 8 Construction methods under the same network infrastructure capability |
| 表 9 网络设施能力不同下的建设方式 Tab. 9 Construction methods under the different network infrastructure capability |
由于多目标求解所得是一近似值,因此对不同权重组合下的设施选址以及目标函数值变化进行分析。
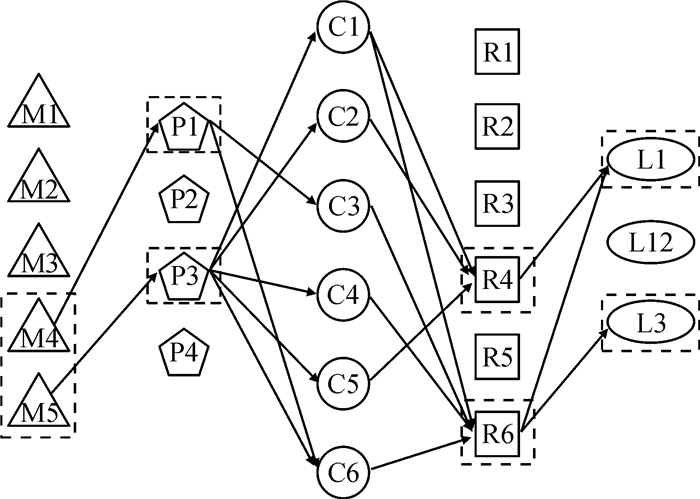
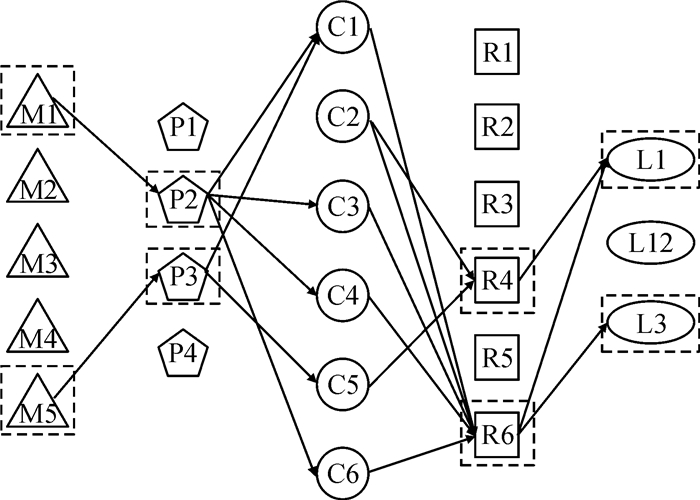
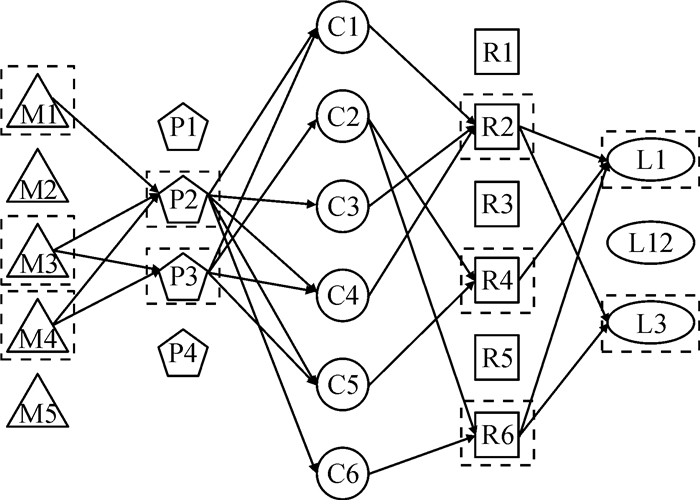
分别对单目标进行求解分析,所得选址方案见图 2~图 4。由图可以看出,制造工厂、配送中心和回收中心的选址存在差异。1)当只考虑闭环供应链网络中运营成本时,选择了建设方式较高、成本较低的M4、M5建制造工厂,P1、P3建配送中心,R4、R6建回收中心,此时需求时间响应成本消耗较大;2)当各地政府和消费者对环境要求较高时,选择了建设方式较低、运输过程中碳排放较小的M1、M5、P2、P3建设备选设施;3)当消费者对服务水平要求较高时,选择了建设方式较低、相对集中的M1、M3、M4建设制造工厂,R2、R4、R6建设回收中心,此时总运营成本和碳排放成本消耗较大。此外,当各目标函数权重变化时,通过对运营成本、碳排放成本、时间响应成本权重调整发现,运营成本和碳排放成本变化并不大,且对总目标影响较小,而时间相应成本会因权重不同变化较大,对总目标函数影响大于其他两者。
|
图 2 运营成本最小选址图 Fig. 2 Operating costs minimum location |
|
图 3 碳排放成本最小选址图 Fig. 3 Carbon emission cost minimum location |
|
图 4 需求时间响应成本最小选址图 Fig. 4 Demand time respond cost minimum location |
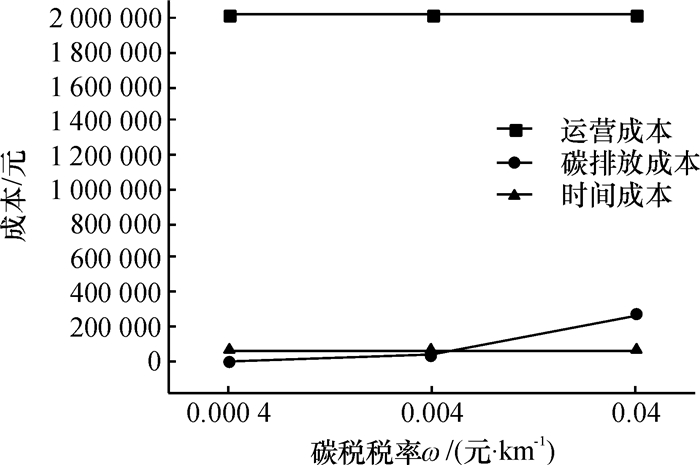
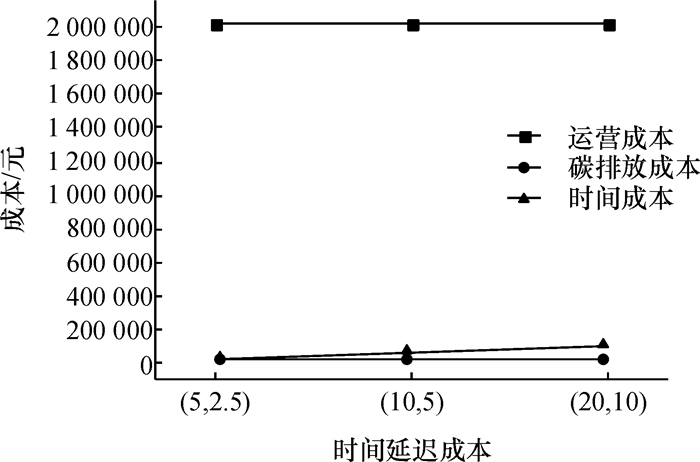
另外,分别对碳税税率与时间延迟成本进行灵敏度分析,并利用Lingo11.0求解相关指标,得到图 5和图 6。当碳税税率ω变化时,随着碳税税率增大,碳排放成本增加,但是碳排放成本增加的比例要小于碳税税率增加的比例,总体看网络中碳排放量在减少,而时间成本有缓慢增长的趋势,说明网络中需求响应时间变长。故而碳税税率的增大,导致设施建设方式等级由高向低转变,说明企业在选址时会更倾向于初始参数较低区域且等级较低的方式进行建设,有利于节约成本, 保护环境和提高服务水平。当单位时间延迟成本增大时,顾客需求响应时间成本增大,但是其增大的比例要小于延迟成本参数增大的比例,由此可见消费者对产品需求响应的速率变快,而网络中碳排放成本与运营成本波动不大。因此,随着延迟成本参数增大,导致设施在建设方式的选择上更倾向于较低等级且设施初始参数较低区域进行建设,这样有利于企业节约成本, 保护环境和提高服务水平。
|
图 5 碳税税率的灵敏度分析 Fig. 5 Sensitivity analysis of carbon tax |
|
图 6 时间延迟成本的灵敏度分析 Fig. 6 Sensitivity analysis of time delays cost |
由于供应链网络优化问题涉及多个经济主体、大量参数变量与约束条件,使得其在建模时呈现出多目标、不确定性等特点,所以说,供应链网络优化设计问题是一个较为复杂的难题。本文建立了一个具有多个供应商、多个制造商、多个配送中心、多个消费者、多个回收中心以及多个处理中心的多层级多目标闭环供应链网络模型,针对单一产品,同时考虑网络设施能力限制、碳税税率、时间延迟成本等方面的影响,以网络运营成本、碳排放成本和顾客需求响应时间成本为目标建立模型。通过求解可以确定闭环供应链网络中各设施的选址、建设方式以及设施间的流量分配,发现在分别考虑单一目标以及相应参数增大时,各设施在建设方式选择上从高级别向低级别转变,且选择建设成本较低、交通便利的地方建厂,有利于企业降低成本, 减少碳排放和提高物流服务水平,并为企业提供决策支持。
| [1] |
侯玉梅, 杨海江. 低碳经济视角下闭环供应链网络优化研究[J].
物流工程与管理, 2014, 36(5): 144-148.
HOU Yumei, YANG Haijiang. Closed-loop supply chain network optimization based on low carbon economy[J]. Logistics Engineering and Management, 2014, 36(5): 144-148. |
| [2] |
SOUZA G C, GUIDE Jr D R, VAN WASSENHOVE L N, et al. Time value of commercial product returns[J].
Management Science, 2006, 52(8): 1200-1214.
DOI: 10.1287/mnsc.1060.0522. |
| [3] |
吕品. 基于最小碳排放的绿色供应链网络设计模型研究[J].
物流技术, 2013, 32(4): 224-226.
LYU Pin. Study on model of green supply chain network based on minimum carbon emissions[J]. Logistics Technology, 2013, 32(4): 224-226. |
| [4] |
沈连梅, 杨勇生, 杨斌, 等. 考虑碳排放的多目标闭环物流网络选址规划[J].
武汉理工大学学报:交通科学与工程版, 2014, 38(2): 409-412.
SHEN Lianmei, YANG Yongsheng, YANG Bin, et al. Considering carbon emissions multi-objective closed-loop logistics network site planning[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering, 2014, 38(2): 409-412. |
| [5] |
KANNAN D, DLABAT A, ALREFAEI M, et al. A carbon footprint based reverse logistics network design model[J].
Resources Conservation and Recycling, 2012, 67: 75-79.
DOI: 10.1016/j.resconrec.2012.03.005. |
| [6] |
YANG J, GUO J, MA S. Low-carbon city logistics distribution network design with resource deployment[J].
Journal of Cleaner Production, 2013, 119: 223-228.
|
| [7] |
ZHANG X, LIU P, LI Z, et al. Modeling the effects of low-carbon emission constraints on mode and route choices in transportation networks[J].
Procedia-Socialand Behavioral Sciences, 2013, 96: 329-338.
DOI: 10.1016/j.sbspro.2013.08.040. |
| [8] |
高举红, 王瑞, 王海燕. 碳补贴政策下闭环供应链网络优化[J].
计算机集成制造系统, 2015, 21(11): 3033-3040.
GAO Juhong, WANG Rui, WANG Haiyan. Closed-loop supply chain network design under carbon subsidies[J]. Computer Integrated Manufacturing Systems, 2015, 21(11): 3033-3040. |
| [9] |
杨建华, 郭继东, 马书刚. 碳税约束的城市冷链物流配送网络设计[J].
工业工程, 2012, 15(5): 86-91.
YANG Jianhua, GUO Jidong, MA Shugang. Distribution network design for carbon tax-constrained urban cold chain logistics[J]. Industrial Engineering Journal, 2012, 15(5): 86-91. |
| [10] |
伍星华, 王旭, 代应. 再制造闭环物流网络的多周期优化设计模型[J].
计算机集成制造系统, 2011, 17(9): 2015-2021.
WU Xinghua, WANG Xu, DAI Ying. Multi-period optimal design model for closed loop remanufacturing logistics network[J]. Computer Integrated Manufacturing Systems, 2011, 17(9): 2015-2021. |
| [11] |
涂南, 昌柳枫, 麦合迪, 等. 考虑设施扩展的闭环物流网络多目标优化[J].
工业工程, 2013, 16(5): 54-61.
TU Nan, CHANG Liufeng, Mehrdad Mehrdod, et al. Multi-objective optimization of closed-loop logistics network with facility expansion[J]. Industrial Engineering Journal, 2013, 16(5): 54-61. |
| [12] |
孙浩, 张桂涛, 钟永光, 等. 政府补贴下制造商回收的多周期闭环供应链网络均衡[J].
中国管理科学, 2015, 23(1): 56-64.
SUN Hao, ZHANG Guitao, ZHONG Yongguang, et al. The equilibrium of multi-period closed-loop supply chain network with manufacturer-collection channel under government subsidies[J]. Chinese Journal of Management Science, 2015, 23(1): 56-64. |
| [13] |
EL-SAYED M, AFIA N, KHARBOTLY A. A stochastic model for forward-reverse logistics network design under risk[J].
Computer and Industrial Engineering, 2010, 58(3): 423-431.
DOI: 10.1016/j.cie.2008.09.040. |
| [14] |
PISHWAEE M S, RABBANI M, TORABI S A. A robust optimization approach to closed-loop supply chain network design under uncertainty[J].
Applied Mathematical Modelling, 2011, 35(2): 637-649.
DOI: 10.1016/j.apm.2010.07.013. |
| [15] |
FENIES P, LAGRANFE S, TCHERNEC N. A decisional modeling for supply chain management in franchised networks: application in franchise bakery networks[J].
Production Planning & Control, 2010, 21(6): 595-608.
|
| [16] |
公绪霞, 齐二石, 刘亮. 基于模糊优化理论的装配线平衡多目标优化[J].
机械设计与制造, 2013(7): 247-250.
GONG Xuxia, QI Ershi, LIU Liang. Multi-objective optimization for assembly line balancing problem based on fuzzy optimization theory[J]. Machinery Design & Manufacture, 2013(7): 247-250. |
| [17] |
李荣钧.模糊多准则决策理论与应用[M].北京:科学出版社, 2002: 262-276.
|
 2016, Vol. 19
2016, Vol. 19