2. 华南理工大学 工商管理学院,广东 广州 510640
2. School of Business Administration, South China University of Technology, Guangzhou 510640, China
众所周知,变质性产品的价值会随着时间的流逝而快速下降。在清晨采购的水果和蔬菜,到了晚上则有部分已经变质。为了对此问题开展研究,Ghare和Schrader[1]首先通过假设产品的损耗率服从指数分布,推导出了具有固定损耗率的经济订货批量模型。在此后的数十年中,有关变质性产品的研究受到了学者们的广泛关注。Liao等[2]在需求依赖于初始库存水平的情形下,考虑了信用支付周期与销售期不一致时,变质性产品的最优订货量。Sana和Chaudhuri[3]在考虑通货膨胀的影响下,解决了变质率服从两参数Weibull分布的库存模型;Ghosh和Chaudhuri[4]在假设产品的变质率服从两参数Weibull分布的情形下,建立了需求率是时间的二次函数时,变质性物品的库存模型。Chung和Liao[5]则考虑了销售变质性产品零售商的订货量必须达到一定数量才可享受信用支付的权利;Huang[6]在文献[5]的基础上考虑了当零售商的订货量达不到某一数量下可以享有部分信用支付权利的情形,即允许一定比例的货款延期支付;Patnaik和Rao[7]则在需求与现有库存负相关时,讨论了变质性产品的最优库存策略;Yang等[8]在供应商向零售商提供临时价格并且零售商仓库容量有限的情况下,讨论了变质性产品的库存模型;Tripathi和Tomar[9]在时变需求且具有临时价格折扣下,分析了变质性产品库存模型;闵杰等[10]则考虑了零售商对客户实施带有等级区别的信用支付策略时,变质性产品的库存策略问题。但是,这些文献并没有考虑多个零售商可以协调订货的情况,更没有讨论多个零售商订购变质性产品的订货决策。
但是,销售变质性产品企业在实际运作中,为了降低成本,它们会寻求与供应链中同层的其他企业进行联合采购的合作。近年来,一些学者对于销售非变质性产品的零售商库存合作联盟展开了分析,例如,Meca等在经典的EOQ和EPQ框架下对此问题进行了一系列的研究。Meca等[11]讨论了n个零售商协调订货周期的库存博弈问题,建立了库存成本博弈和持有成本博弈两类库存合作博弈模型;在文献[11]的基础上Meca等[12]又考虑了零售商具有缺货成本的一般库存成本博弈和持有成本博弈问题,并证明了这两种博弈都是完全平衡的,即存在一种分配方案使零售商留在大联盟中;此外,Meca等[13]还考虑了零售商联合订货时可获得临时价格折扣的库存合作博弈问题,并将其定义为p可加博弈。但是,以上的文献并没有考虑变质性产品对联盟订货量决策、成本的分摊规则和联盟稳定性的影响。而冯海荣等[14]则从合作博弈论的角度讨论了多零售商向同一供应商联合采购某种易腐品的订货决策及费用分配问题,他们指出多个零售商形成联盟所分摊的成本比原来各自独立运营的成本要低。但是,他们并没有讨论零售商的产品可以联合配送的情况,而在实际中,联合采购的产品往往都是由供应商或者第三方物流公司统一配送的。例如,2011年,广东省教育厅组织广州地区23所高校后勤部门以及餐饮中心负责人到广州江南果菜批发市场,进行原材料的集中采购与统一配送①。关于多个零售商进行联合采购与配送的合作模式,吸引了企业界的经理人和学术界研究人员的关注。目前,仅Fiestras Janeiro等[15]在经典的EOQ框架下,讨论了多个零售商联合运输时的成本分摊问题。但是,他们并未考虑变质性产品对联盟订货决策及稳定性的影响。
① http://news.cnwest.com/content/2011-03/17/content_4288350.htm
本文在上述研究的基础之上,考虑销售变质性产品的零售商联合采购和运输联盟的订货策略、成本分摊规则及其稳定性,得到了变质性产品联合采购与运输联盟的最优订货策略;随后指出零售商的采购与运输联盟并不一定能降低各自的成本,并给出了合作可以降低各自成本的条件(即满足次可加性的条件);在合作博弈满足次可加性的条件下,根据边际成本给出了可行的成本分摊规则,并证明了在此分摊规则下,可以保持大联盟的稳定。
1 联合采购与运输联盟的订货量决策 1.1 符号与假设Qi为零售商i(i=1, 2, …, n)的订货量;
Di为零售商i单位时间的需求量;
ai为供应商到零售商i的运输成本,与供应商到零售商之间的距离成正比;
hi为零售商i单位时间单位产品的持有成本;
Ti为零售商i独立订货时的订货周期;
Ii(t)为零售商i在t时刻的库存水平;
c为零售商订购产品的单位成本;
a为补货启动费用;
α为产品单位时间的变质率;
TS为零售商联盟S的统一订货周期。
假设1 采购与运输联盟中零售商的各种信息是完全共享的;
假设2 产品的补货能力无限大,不允许缺货;
假设3 假设零售商均位于一条直线上,如果多个零售商形成联合采购与运输联盟S,则联盟S的运输成本为联盟中与供应商距离最远零售商的运输成本,即aS=max{ai|i∈S}。
1.2 模型的建立与求解当每个零售商独立订货时,零售商i向供应商发出订单。由于产品的补货能力无限大,则可立即以运输成本ai收到货物。产品在运输和销售的过程中会发生变质,而变质的产品会立即退出销售。因此,在一个订货周期Ti内,零时刻的库存水平为Qi,随着需求的累积和变质性产品的处理,在一个周期结束后,库存水平降为0。设零售商i在时刻t ∈[0,Ti]时间内的库存水平Ii(t)满足下列方程: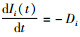
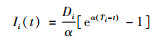
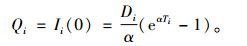
|
(1) |
销售变质性产品零售商i单位时间内采购与运输总成本为
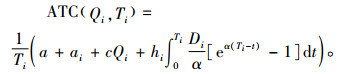
|
(2) |
将式(1)代入式(2)可得
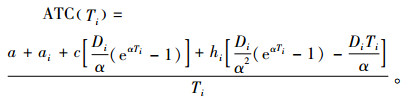
|
(3) |
如果m(1≤m≤n)个零售商形成联合采购与运输联盟S后,将会以统一的订货周期TS向供应商订货,并且产品从供应商到m个零售商将进行统一的配送。本文假设n个零售商均在一条直线上,因此,零售商联盟S的运输成本为aS =max{ ai |i∈S}。变质性物品联合采购与运输联盟的订货库存水平随时间变化规律如图 1所示。
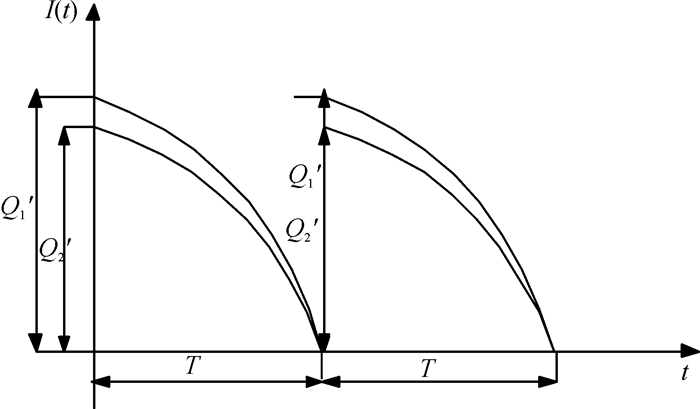
|
图 1 销售变质性产品联合采购与运输联盟的库存水平 Fig. 1 Inventory level of retailers' joint purchasing and transportation coalition for deteriorating items |
因此,根据式(3)可知变质性产品联合采购与运输联盟的总成本为
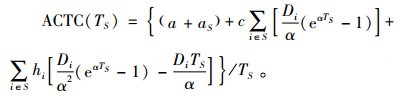
|
(4) |
由eαT泰勒展开式可知,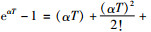
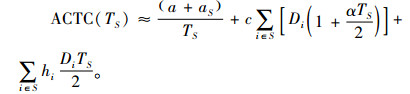
|
对ACTC(TS)关于TS求二阶导数,可知,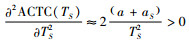
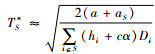
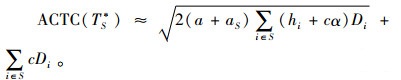
|
(5) |
本节将首先说明零售商进行联合采购与运输并非总是对其自身有利的;其次将讨论零售商参与联合采购与运输合作对自身有利的条件;随后,在零售商参与变质性物品的联合采购与运输合作的情形下,讨论联盟将如何对总成本进行分摊,可使得每个零售商都留在联盟中而不叛逃出去。在合作博弈论中,与这两个问题相对应的概念分别是“次可加性”与“合作博弈的解”。零售商可以选择参与不同的联合采购与运输联盟。不同的联盟将会产生不同的运作成本,联盟的成本可以用一个特征函数刻画,定义为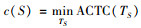
定义1 如果对于任意S, T⊆N,且S∩T=∅,有c(S)+c(T)≥c(S∪T),则称合作博弈(N, c)具有次可加性。
下面的例1将说明变质性物品的联合采购与运输联盟不一定满足次可加性。
例1 在由两个零售商所组成变质性产品的采购与运输系统中,假设零售商每次订货的固定成本为a=20,可变订货成本为c=15,并且产品从供应商到零售商1和2的运输成本分别为a1=20和a2=100,零售商1和2所面对的产品需求分别为D1=800和D2=300,零售商1和2的库存持有成本分别为h1=2和h2=1,产品的变质率为α=0.05。由式(5)可知,零售商1、零售商2以及零售商联合采购与运输联盟的成本则分别如下所示。
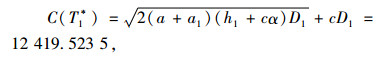
|
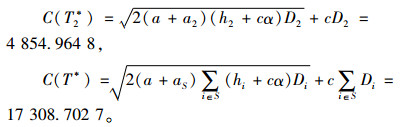
|
可知,C(T1*)+C(T2*)=17 274.488 3<C(T*)= 17 308.702 7。从而说明在此组参数下,合作博弈(N, c)不满足次可加性,即零售商1和2结盟并不能对自身有利。
定理1给出了零售商参与联合采购与运输合作对自身有利的条件,即合作博弈(N, c)满足次可加性的条件,本文随后的讨论都在满足此条件的情形下讨论。
定理1 对于任意的S、T⊆N,满足S∩T=∅且aT>aS,则当且仅当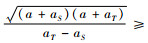
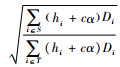
证明 设任意的S、T⊆N,满足S∩T=∅且aT>aS。为了证明的方便,定义一个新的合作博弈(N,c),其中,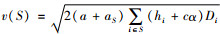
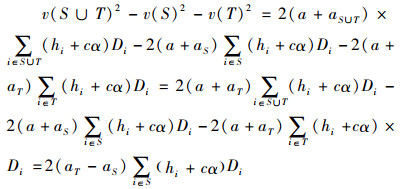
|
由于v(S)+v(T)≥v(S∪T),因此,2v(S)v(T)≥v(S∪T)2-v(S)2-v(T)2,从而可知对任意的S, T⊆N,满足S∩T=∅且aT>aS,满足次可加性的条件为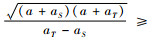
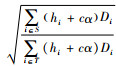
定义2 满足如下条件的集合称为合作博弈(N, c)的核。
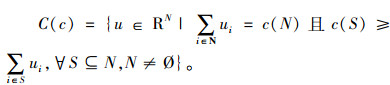
|
定义3 给定合作博弈(N, v),对每个i∈N和满足i∈S的S⊆N,参与者i对联盟S的边际贡献是mi(N, v)=v(S)-v(S\i)。
令π(N)是N的所有置换σ:N→N的集合,集合Pσ(i):={r∈N|σ-1(r)<σ-1(i)}含有关于置换σ的所有i的前继。
定义4 关于置换σ和合作博弈(N, v)的边际贡献向量mσ(N, v)∈Rn,定义为对所有i∈N,mσ(N, v)的第i个分量为miσ(N, v):=v(Pσ(i)∪{i})-v(Pσ(i))。
定义5 Shapley值合作博弈(N, v)的Shapley值将大联盟N的成本v(N)按照下述公式进行分配:
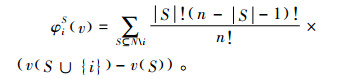
|
其中,|S|表示联盟S中的参与人个数; c(∅)=0。
在合作博弈(N, c)满足次可加性的情形下,若将零售商按照其与供应商之间的距离由远及近降序排列的全体记为π(N, A),则变质性物品联合采购与运输大联盟N的运作成本可按如下规则进行分摊。
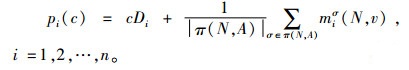
|
(6) |
定理2 成本分摊规则p(c)=(p1(c), p2(c), …, pn(c)是变质性物品联合采购与运输合作博弈的一个核配置。
证明1)对于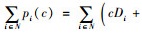
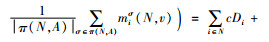
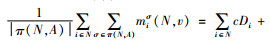
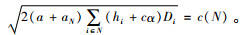
2) a如果联合运输与采购联盟S中含有距供应商最远的零售商σ-1(1),则有
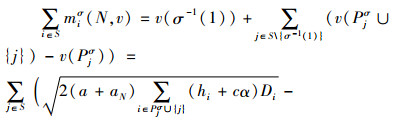
|
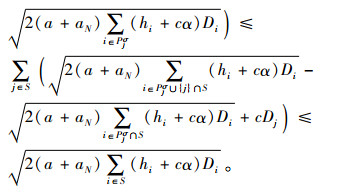
|
由于,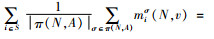
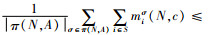
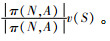
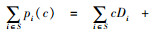
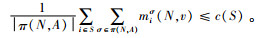
b如果联合采购与运输联盟S中不包含距供应商最远的零售商σ-1(1)。则令S=S∪{σ-1(1)},可知,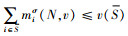
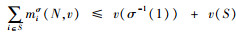
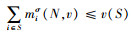
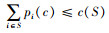
本节将通过数值例子,对比3种成本分摊规则。假设所考虑的变质性物品联合采购与运输系统中仅有3个零售商,3个零售商的参数如表 1所示。
| 表 1 3个零售商的参数 Tab. 1 Parameters of three retailers |
通过表 2可知,在表 1所给出的参数下,变质性产品的联合采购与运输合作博弈满足次可加性。
| 表 2 联合采购与运输合作博弈的次可加性 Tab. 2 Subadditivity of joint purchasing and transportation cooperative game |
| 表 3 联合采购与运输联盟的运作成本 Tab. 3 Operating cost of joint purchasing and transportation coalition |
1) 由系统给定的参数可知,π(N, A)={(3, 2, 1)}。根据式(6)可知,按分配规则p所给出的成本分摊方案为, (12 001.2, 7 500, 6 979.8)。
2) 平均分配方案为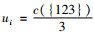
3) Shapley值分配方案为φ=(12 194, 7 792.5, 6 494.5),其中,3个零售商的6种排序情况下所得到的成本分摊份额分别为:(12 580,7 699,6 202),(12 580, 7 500,6 401),(12 001.2,8 277.8,6 202),(12 001,8 277.8,6 202.2),(12 001.2, 7 500, 6 979.8),(12 001, 7 500.2, 6 979.8)。
虽然在这组参数下,Shapley值分配方案在联合采购与运输合作博弈的核中,但需要计算零售商的所有的排序。而给出的成本分摊方案仅仅需要计算一种排序的情况,就能得到相似的结果并且仍然在变质性物品联合采购与运输合作博弈的核中。特别当零售商的个数较多时,所给出的成本分摊方案的优势更加明显。
4 总结本文以多个销售变质性产品的零售商为研究背景,建立了变质性产品零售商形成联合采购与运输联盟的稳定性模型。在确定性需求下得到了变质性产品联合采购与运输联盟的最优订货策略;随后指出零售商的采购与运输联盟并不一定能降低各自的成本,并给出了合作可以降低各自成本的条件(即满足次可加性的条件);根据边际成本给出了可行的成本分摊规则,并证明了在此分摊规则下,可以保持大联盟的稳定。随后通过数值例子发现,Shapley值分配方案在联合采购与运输合作博弈的核中,但是,其需要计算零售商的所有排序;而本文说给出的成本分摊方案仅仅需要计算一种排序的情况,就能得到相似的结果并且仍然在变质性物品联合采购与运输合作博弈的核中。当零售商的个数较多时,所给出成本分摊方案的优势更加明显。
| [1] |
GHARE P, SCHRADER G. A model for exponentially decaying inventory[J].
Journal of Industrial Engineering, 1963, 14(5): 238-243.
|
| [2] |
LIAO H C, TSAI C H, SU C T. An inventory model with deteriorating items under inflation when a delay in payment is permissible[J].
International Journal of Production Economics, 2000, 63(2): 207-214.
DOI: 10.1016/S0925-5273(99)00015-8. |
| [3] |
SANA S, CHAUDHURI K. An EOQ model with time-dependent demand, inflation and money value for a ware-house enterpriser[J].
Advanced Modeling and Optimization, 2003, 5(2): 135-146.
|
| [4] |
GHOSH S, CHAUDHURI K. An order-level inventory model for a deteriorating item with Weibull distribution deterioration, time-quadratic demand and shortages[J].
Advanced Modeling and Optimization, 2004, 6(1): 21-35.
|
| [5] |
CHUNG K J, LIAO J J. Lot-sizing decisions under trade credit depending on the ordering quantity[J].
Computers & Operations Research, 2004, 31(6): 909-928.
|
| [6] |
HUANG Y F. Economic order quantity under conditionally permissible delay in payments[J].
European Journal of Operational Research, 2007, 176(2): 911-924.
DOI: 10.1016/j.ejor.2005.08.017. |
| [7] |
PATNAIK V P R, RAO K S. Optimal ordering policies of an inventory model for deteriorating items with demand inversely proportional to the on-hand inventory[J].
International Journal of Operational Research, 2012, 13(2): 200-218.
DOI: 10.1504/IJOR.2012.045187. |
| [8] |
YANG C T, OUYANG L Y, WU K S, et al. Optimal ordering policy in response to a temporary sale price when retailer's warehouse capacity is limited[J].
European Journal of Industrial Engineering, 2012, 6(1): 26-49.
DOI: 10.1504/EJIE.2012.044809. |
| [9] |
TRIPATHI R, TOMAR S S. Optimal order policy for time-dependent deteriorating items in response to temporary price discount linked to order quantity[J].
Applied Mathematical Sciences, 2013, 58(7): 2869-2878.
|
| [10] |
闵杰, 徐小明, 张家精, 曹宗宏.等级信用支付策略下变质性产品的库存优化模型[J].运筹与管理, 2014, 23(6):29-36.
MIN J, XU X M, ZHANG J J, et al. Inventory optimization model for deteriorating items under grade trade credit policy[J]. Operations Research and Management Science, 2014, 23(6):29-36. |
| [11] |
MECA A, TIMMER J, GARCÍA-JURADO I, et al. Inventory games[J].
European Journal of Operational Research, 2004, 156(1): 127-139.
DOI: 10.1016/S0377-2217(02)00913-X. |
| [12] |
MECA A, GARCÍA-JURADO I, BORM P. Cooperation and competition in inventory games[J].
Mathematical Methods of Operations Research, 2003, 57(3): 481-493.
DOI: 10.1007/s001860200253. |
| [13] |
MECA A, GUARDIOLA L A, TOLEDO A. P-additive games: a class of totally balanced games arising from inventory situations with temporary discounts[J].
Top, 2007, 15(2): 322-340.
DOI: 10.1007/s11750-007-0020-5. |
| [14] |
冯海荣, 李军, 曾银莲. 易腐品供应链企业联合采购决策与费用分配研究[J].
系统科学与数学, 2011, 31(11): 1454-1466.
FENG H R, LI J, ZENG Y L. Study on collaborative purchasing and cost allocation problem in supply chains with perishable products[J]. Journal of Systems Science and Mathematical Sciences, 2011, 31(11): 1454-1466. |
| [15] |
FIESTRAS-JANEIRO M, GARCÍA-JURADO I, MECA A, et al. Cost allocation in inventory transportation systems[J].
Top, 2012, 20(2): 397-410.
DOI: 10.1007/s11750-011-0207-7. |
 2016, Vol. 19
2016, Vol. 19