失效模式与影响分析(failure mode & effects analysis, FMEA)是一种用于风险分析和预防的技术,其重心是事前预防失效发生[1]。它的核心是对失效从严重度S(Severity)、发生度O(Occurrence)和难检度D(Detection)3个维度来评估风险,并加以控制, 从而将风险减少到可接受的水平[2]。分析人员使用这3个维度以及RPN(risk priority number)法对失效模式进行评价和优先级排序,筛选出优先级最高的失效模式。鉴于失效模式与失效原因的“一对多”关系,分析人员依据其失效原因提出相应的改善方案,再次采用同样的维度和方法进行评价和排序,得到改善方案实施的优先级顺序。
因为应用环境与目的的改变以及RPN方法本就存在的许多局限性[3-7],在采用同样的3个维度和RPN法进行第二次评价和排序时,很多不适用问题就暴露出来了。
1) 将FMEA方法中的术语死板地用于质量改善方案评价排序之中,会因为背景差异导致难以理解。
2) 三个风险维度严重度S、发生度O和难检度D的评价具有不确定性、不精确性和模糊性。例如,专家的评判语言一般都有“可能”、“很重要”等模糊描述,而原方法一般采用1-10这样的精确数字,必然会造成误差。
3) 在原RPN方法中,严重度S、发生度O和难检度D的权重是相等的,不同的严重度S、发生度O和难检度D评价值,经过计算后可能得到相同的RPN值。这个局限仍然存在于改善方案实施的优先级排序过程中。
4) 风险顺序数RPN是由严重度S、发生度O和难检度D相乘得来的。这种倍增的方法使RPN值对三个风险因素的变化很敏感。
5) 在原RPN方法中,并没有科学的设定界值进行分档,只是依据分析人员的经验来判定一个界值。这可能造成轻视重要的改善方案,或因实施无价值的方案造成巨大的浪费。
鉴于这些局限性,本文从以下方面展开研究和应用。
1) 重新定义FMEA中的关键术语,使其更好地应用于改善方案的评价和优先级排序中。
2) 借助语言评价和三角模糊数获得更合理、准确的决策指标值和主观权重;采用熵权法获得客观权重,进而得到决策指标的组合权重。
3) 利用基于改进三角模糊数距离测度的TOPSIS法进行改善方案优先级排序,使用RSR法对改善方案分档。最后,采用一个企业实例验证上述方法的有效性和可行性。
1 FMEA关键术语的重新界定为了更好地适用质量改善项目实施的优先级排序,FMEA的一些术语需要进行适当地重新界定。
(1) 失效模式置换为改善主题。
传统FMEA中的失效模式是指工程中可能发生的不满足过程要求和设计意图的问题点[2]。当产品功能缺失或者存在不符合要求的过程时,分析人员来定义“失效模式”。而在质量改善项目选择时,沿用失效这一概念会造成理解混乱。根据质量改善项目的背景和特点,本文定义为“改善主题”,是与失效模式所有可能的失效原因相对应的改善方案。
(2) 严重度S、发生度O和难检度D置换为难易程度D、发生度O和改善潜力P。
传统FMEA中严重度S是失效模式所产生影响的等级值。本文定义为难易程度D(Difficulty),重点是对改善已发生问题和低水平环节的成本、效益、可行性和解决能力的综合评估。
发生度O原意是指失效原因引起失效结果的可能性大小。在质量改善项目中仍沿用这个术语,强调的是如果不进行改善,已发生问题再次发生的可能性和低水平环节导致问题出现的可能性。
难检度D原意是采用现行的过程控制可以检测到失效模式由某种肯定的原因激发的可能性大小。本文定义为改善潜力P(Potential),强调质量改善项目现状与行业水平值的差距大小。
根据改善的快速易实施原则,难易程度D越小、发生度O越大、改善潜力P越小,质量改善项目的优先级顺序越大。
2 指标值及权重的确定 2.1 模糊集理论确定指标值在FMEA分析过程中存在很多模糊语言话语,如“一般”、“很重要”、“可能”“也许”等。如果以精确的数字来确定这些模糊性语言的等级,可能出现较大的偏差。模糊集理论可以将这些模糊语言变量用模糊数来表示,充分考虑了分析人员的模糊主观判断,使得评估更加客观。
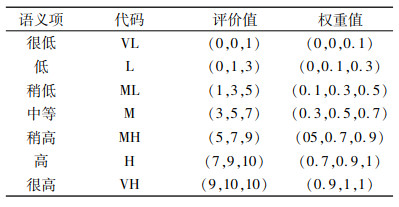
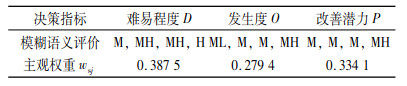
模糊数是基于实数集的模糊子集。在实际运用中,用得比较广泛的模糊数是三角模糊数。选取“很低”、“低”、“稍低”、“中等”、“稍高”、“高”、“很高”7个语义项来评估这3个决策指标的值及其权重[8]。表 1中的评价等级给出了专家对于各个改善主题的决策指标的评价等级和权重等级。
| 表 1 改善主题LPi决策指标的语义变量评价等级 Tab. 1 Linguistic variables evaluation grade |
本文引入模糊数的等级均值积分来获得三角模糊数的清晰数。根据等级均值积分的定义,一个三角模糊数A=(a, b, c)可以进行解模糊化计算,得到一个清晰数。

|
(1) |
通过文献调查发现,许多关于FMEA中失效模式风险排序问题的研究,在确定决策指标的权重时,大多是专家群体主观的赋予决策指标不同权重。这必然会造成较大的误差。为了更加充分地利用专家的知识和经验,本文采用主观和客观赋权的方法来确定决策指标的权重。
假设共有m个不同的改善主题LP1, LP2, …, LPn,由n个决策指标对其进行评价。有k名专家依据第j个决策指标Cj(j=1, 2, 3…, n)对每一个改善主题进行评价,其中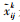
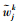
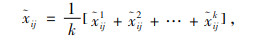
|
(2) |
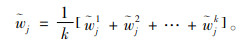
|
(3) |
将专家对改善主题的决策指标的语义评价用三角模糊数表示,依据式(1)获得决策指标的清晰数,得到第k个专家对第j个决策指标的评估值wjk,然后进行归一化处理,最终得到决策指标的主观权重wsj。
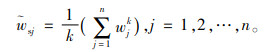
|
(4) |
熵权法是挖掘数据内部规律的有效方法,相对于主观赋权方法,精度较高客观性更强,可以有效降低人为因素等对赋权的影响,更好地解释所得到的结果,是一种有效的客观赋权方法。熵权法的计算步骤:
1) 构建模糊评价矩阵D
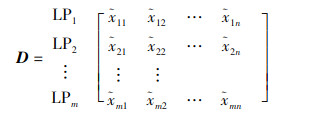
|
(5) |
2) 构建规范化评价矩阵R=(rij)m×n。
一般地,最常见的属性类型有效益型B和成本型C,其中效益型属性是指属性值越大越好的属性,成本型属性是指属性值越小越好的属性[9]。
将评价矩阵D=(xij)m×n转化为规范化矩阵R=(rij)m×n,利用下列规范模糊评价矩阵的计算公式。
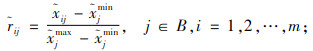
|
(6) |
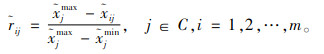
|
(7) |
3) 计算第j项决策指标下,第i个改善主题的特征比重。
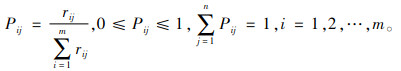
|
(8) |
4) 计算每一个决策指标的熵值。计算过程如式(9)。
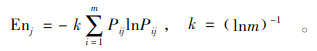
|
(9) |
5) 计算各个决策指标的差异系数。差异系数越大,对改善主题评价的作用越大,决策指标的权重系数就越小。差异系数的计算等式为
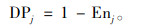
|
(10) |
6) 使用熵权法对决策指标进行赋权,得到每个决策指标的客观权重woj。
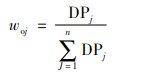
|
(11) |
将专家主观权重和熵权法得到的客观权重综合考虑,共同确定决策指标的权重wj。
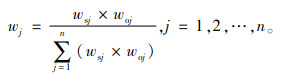
|
(12) |
为了更好地度量各个改善主题与模糊理想解之间的分离程度,本文使用刘华文提出的改进的三角模糊数距离测度来改进TOPSIS法的欧氏距离测度[9]。和媛媛等经过对五种距离公式的实验分析比较,发现这种距离测度公式对改善主题区别能力最强,最终的排序结果可靠性最好,并且随改善主题个数增加其排序结果的变化是最稳定的[10]。
本文将改进的TOPSIS方法用于质量改善项目优先级排序过程,其步骤如下。
1) 构建模糊评价矩阵D。
2) 构建规范化的评价矩阵R=(rij)m×n。
3) 构建考虑决策指标权重的评价矩阵V=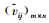
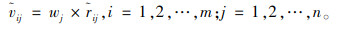
|
(13) |
4) 确定模糊理想解Α+和模糊负理想解Α-。
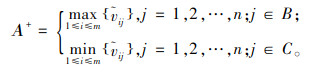
|
(14) |
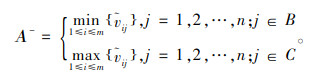
|
(15) |
5) 计算各个改善主题到模糊理想解和模糊负理想解的距离。
假设一个经过加权规范化三角模糊数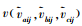
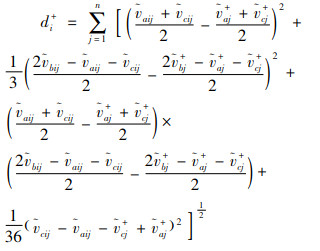
|
(16) |
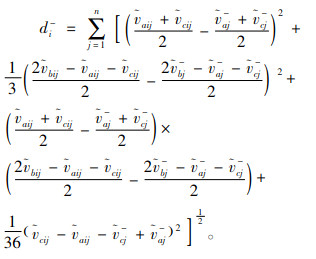
|
(17) |
6) 计算相对贴近度。
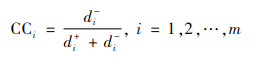
|
(18) |
所以,根据相对贴近度的大小,将其由大到小进行排列,CCi越大,则对应的改善主题的优先级越高。
4 基于RSR法的项目分档秩和比法(Rank-sum ratio,RSR)是我国学者田凤调于1988年提出的,目前此法已日渐完善,广泛地应用于医疗卫生领域的多指标综合评价、统计预测预报、统计质量控制等方面[11-12]。本文在具体应用时,先使用上述改进的TOPSIS法计算各相对贴近度,再借助RSR法对其进行分档,希望获得客观、全面、真实的改善项目优先级排序,并借助RSR法排除没有实施价值的改善项目。
下面将具体介绍其分析的步骤。
1) 对所得的8个相对贴近度CCi进行编秩。编秩原则:因为相对贴近度是高优指标,故对其最大值编以8,次大值编以7,再依次类推到最小值编以1。
2) 计算RSR值,其计算公式为
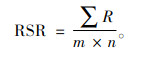
|
(19) |
其中,m为指标数(本文由于只考虑相对贴近,故其设为1);n为样本数(本文对应为8);R为步骤(1)中编秩的秩次。
3) 确定RSR分布,将其按照从小到大排列起来,分别计算各RSR对应的频数f,向下累积频数f′,秩次范围R,平均秩次R和向下累计频率pi(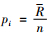
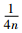
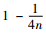
4) 求出相应的回归方程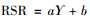
5) 根据常用分档,计算分档的各个临界值,从而确定各个样本所在的分档情况。
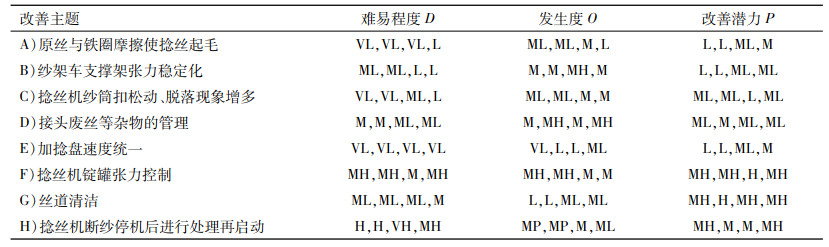
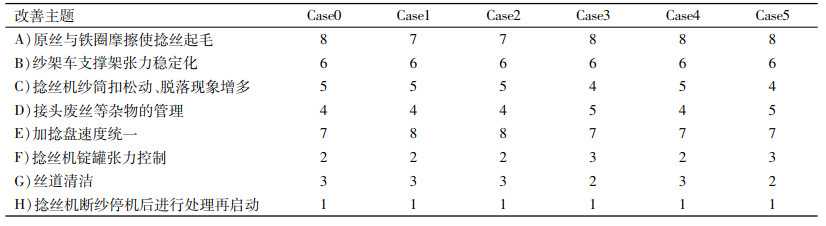
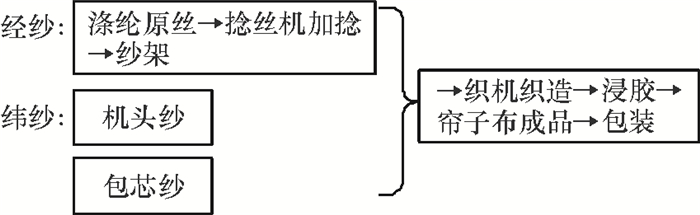
5 实证研究KL公司主要生产轮胎帘子布和汽车安全气囊,其客户中有许多知名的轮胎制造商和汽车制造商。为了提升涤纶浸胶帘子布(DTC)产品的品质,降低成本,提高产品竞争力,进而提高顾客满意度,公司组织了质量改善小组。公司认为与DTC生产相关的设备、技术应作为质量改善重点,具体包括DTC捻丝线品质改善,DTC捻丝机、纱架和配套织机的作业改善,产品外观特性改善。目前,涤纶浸胶帘子布的工艺流程如图 1所示。质量改善小组4位主要成员经过现状调查和原因分析,确定了提升DTC产品品质的8项改善主题,并对改善主题进行评估确定实施顺序。但是企业采用的经验排序方法过于依靠专家经验,对于相关的经验和知识要求较高,不适合普通人员使用。本文采用新的排序方法,改进排序过程。采用模糊语言对其进行评价,如表 2所示。
|
图 1 涤纶浸胶帘子布工艺流程图 Fig. 1 The process flow of polyester tyre cord fabric |
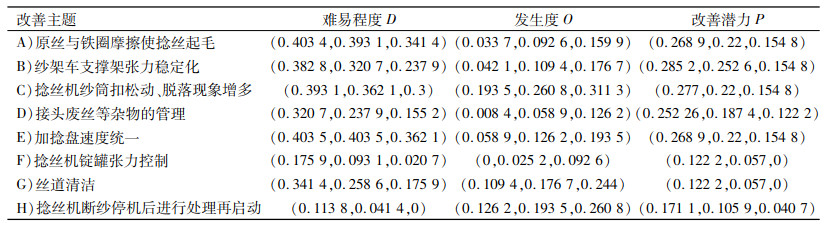
| 表 2 专家对各个改善主题的模糊语义评价 Tab. 2 The fuzzy linguistic evaluation of expert |
使用专家的语言模糊评价来进行决策指标权重的计算,其步骤如下:
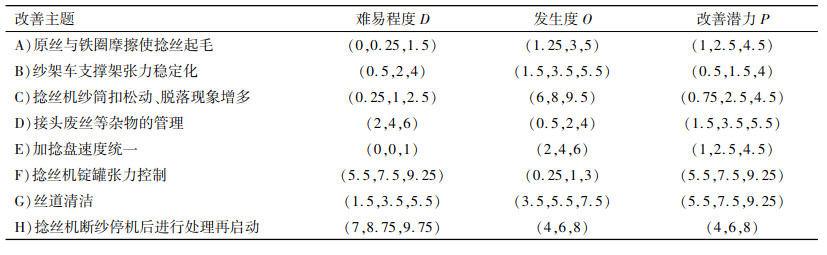
第一步,构建模糊评价矩阵,依据式(2)得到的评价矩阵如表 3所示。
| 表 3 模糊评价矩阵D Tab. 3 The fuzzy evaluation matrix D |
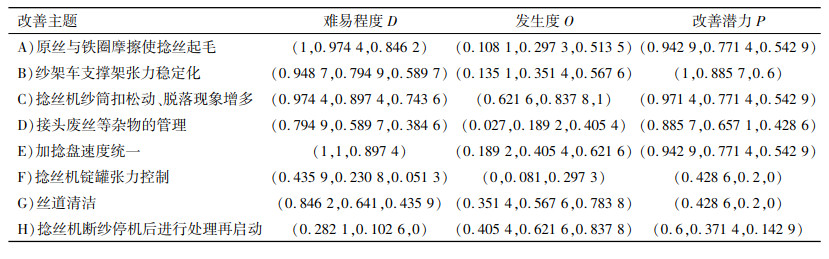
第二步,对评价矩阵进行规范化处理,依据式(6)和(7)计算得到规范化评价矩阵如表 4所示。
| 表 4 规范化评价矩阵R Tab. 4 The standardized evaluation matrix R |
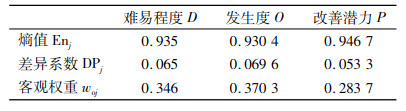
第三步,计算3个决策指标的综合权重。其中,主观权重依据式(4)计算,如表 5所示;使用熵权法进行客观权重赋值,依据式(8)~(11)的计算结果如表 6所示,得到各个改善主题的熵值、差异系数和客观权重。最终的综合权重依据式(12)计算,得到决策指标的综合权重向量wj=(0.403 5, 0.311 3, 0.285 2)。
| 表 5 决策指标的模糊语义评价和主观权重 Tab. 5 Linguistic fuzzy evaluation and subjective weight of decision factors |
| 表 6 决策指标的客观权重 Tab. 6 Objective weight of the decision factors |
使用改进的TOPSIS法进行改善项目的优先级排序,主要步骤如下:
第一步,构建考虑决策指标综合权重的模糊评价矩阵,依据等式(13)计算得到的模糊评价矩阵如表 7所示。
| 表 7 考虑决策指标综合权重的模糊评价矩阵 Tab. 7 Weighted fuzzy evaluation matrix |
第二步,依据等式(14)和(15),确定模糊理想解Α+和模糊负理想解Α-。
Α+=[(0.113 8, 0.041 4, 0), (0.193 5, 0.260 8, 0.311 3), (0.122 2, 0.057, 0)];
Α-=[(0.403 4, 0403 4, 0.362 1), (0, 0.025 2, 0.092 6), (0.285 2, 0.252 6, 0.171 1)]。
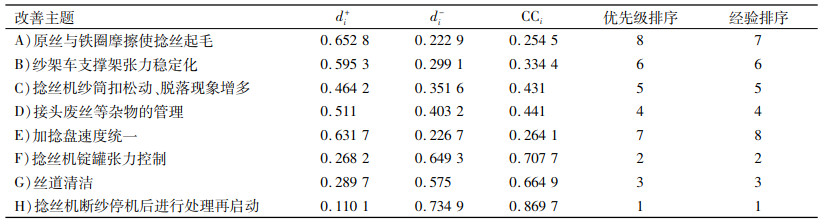
第三步,依据等式(16)~(18),确定各个改善主题距离理想的距离和相对贴近度,并依相对贴近度进行排序。如表 8所示。
| 表 8 各个改善主题和优先级排序 Tab. 8 Priority ranking process of improved themes |
将新方法获得的优先级排序结果与经验排序对比,发现改善主题H“捻丝机断纱停机后进行处理再启动”的优先级都是第1位,质量改善小组应该首先从此主题开始推行质量改善活动。优先级排序对比说明改进的TOPSIS法能够代替经验排序方法,新方法利用综合权重和改进的三角模糊数距离测度,确保了优先级排序的适用性、有效性、科学性和准确性。
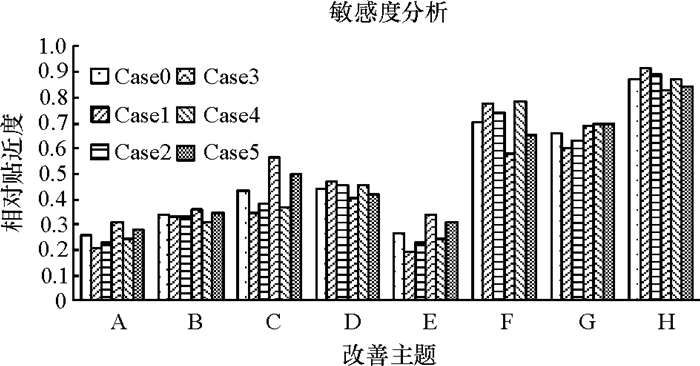
5.3 敏感度分析为了探究新的优先级排序方法对决策指标权重变化的敏感度,本文进行了敏感度分析。表 9是决策指标的各不相同的权重赋值,表 10和图 2是各个改善主题在不同权重赋值情况下的优先级排序。
| 表 9 决策指标的权重赋值 Tab. 9 Weight assignment of decision factors |
| 表 10 改善主题在不同权重赋值情况下的优先级排序 Tab. 10 Priority ranking using different weights assignment |
|
图 2 敏感度分析 Fig. 2 Sensitivity analysis |
表 10显示,在列举的六种情况下,优先级排第1名的改善主题都是“(H)捻丝机断纱停机后进行处理再启动”。在Case3和Case5情况下,“(G)丝道清洁”的优先级排第2名,“(F)捻丝机锭罐张力控制”的优先级排第3名;“(C)捻丝机纱筒扣松动、脱落现象增多”的优先级排第4名,“(D)接头废丝等杂物的管理”的优先级排第5名,其他情况下两对改善主题的排序是相反的。
在新的优先级排序方法中,决策指标权重由主观权重和客观权重综合得来的。为了验证主观权重对排序结果的影响程度,将不同决策指标权重下的相对贴近度大小用图 2表示出来。敏感度分析表明决策指标权重变化或决策指标值的变化对排序结果的影响非常小,改进的TOPSIS法在进行改善项目优先级排序时,大大减少了人为因素带来的波动,稳定性比较强。
5.4 改善项目的分档一些质量改善项目的实施对产品质量追平的提高帮助很有限,甚至得不偿失,事先根据专家评价对改善项目进行科学合理的分档,可以规避无价值项目。在采用改进的TOPSIS法获得相对贴近度后,基于RSR法的项目分档,主要步骤如下:
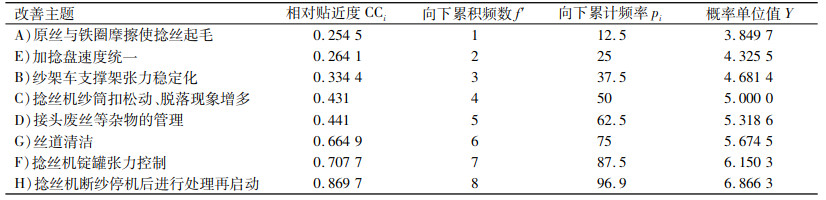
第一步,将8个改善主题依据相对贴近度从小到大进行排列,计算向下累计频数、向下累计频率和概率单位值,如表 11所示。
| 表 11 相对贴近度的秩和比分布 Tab. 11 RSR distribution of CCi |
第二步,利用参数统计中线性回归方法,确定相对贴近度和概率单位值之间的回归关系。运用SPSS19.0进行回归分析,得到相对贴近度与概率单位值之间的线性回归方程为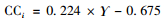
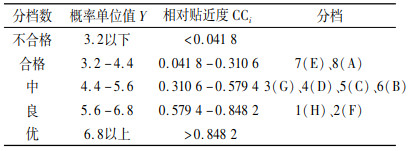
第三步,根据合理分档数表进行分档[12]。将改善主题分为5档,如表 12所示。
| 表 12 改善主题的分档 Tab. 12 Improved themes for different buses |
本次分档显示,H和F改善主题的等级为良,是需要优先对其进行改善实施。G、D、C、B四个改善主题的等级为良,需要次级优先进行改善实施。而分档表示对E和A进行改善实施,可能得不到理想的改善效果。通过RSR法分档,质量改善小组可以忽略低等级的改善项目,将有限的资源集中于中等以上的改善项目,按照优先级排序和等级分档进行改善活动,提升产品的质量水平。
6 结论1) 鉴于FMEA中RPN排序在改善项目优先级排序的不足,重新定义了改善主题、难易程度、发生度和改善潜力等相对应的术语。
2) 基于模糊集理论,采用模糊语言对改善主题进行评价,并且使用熵权法客观赋权,考虑了主、客观综合权重
3) 使用经过三角模糊数距离测度改进的TOPSIS法实现了改善主题的优先级排序,敏感度分析也确认了新排序方法的稳定性。
4) RSR法的分档确定了改善主题的等级,排除了无实施价值的改善项目,避免了浪费。
| [1] |
STAMATAS D H. 故障模式影响分析FMEA从理论到实践[M]. 陈晓彤, 姚紹华, 译. 2版. 北京: 国防工业出版社, 2005.
|
| [2] |
朱宗乾, 罗阿维, 李艳霞, 等. 采用FMEA的ERP项目实施风险分析方法[J].
工业工程, 2010, 13(6): 1-5.
ZHU Zongqian, LUO Awei, LI Yanxia, et al. The implementation of ERP project risk analysis methods using FMEA[J]. Industrial Engineering, 2010, 13(6): 1-5. |
| [3] |
KUTLU A C, EKMEKCIOGLU M. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP[J].
Expert Systems with Applications, 2012, 39(1): 61-67.
|
| [4] |
SONG Wenyan, MING Xinguo, WU Zhenyong, et al. Failure modes and effects analysis using integrated weight-based fuzzy TOPSIS[J].
International Journal of Computer Integrated Manufacturing, 2013, 26(12): 1172-1186.
DOI: 10.1080/0951192X.2013.785027. |
| [5] |
LIU H C, YOU J X, SHAN M M, et al. Failure mode and effects analysis using intuitionistic fuzzy hybrid TOPSIS approach[J].
Soft Computing -A Fusion of Foundations, Methodologies and Applications, 2015, 19(4): 1085-1098.
|
| [6] |
MEHMET E, AHMET C K. A fuzzy hybrid approach for fuzzy process FMEA: an application to a spindle manufacturing process[J].
International Journal of Computational Intelligence Systems, 2012, 5(4): 611-626.
DOI: 10.1080/18756891.2012.718104. |
| [7] |
SONG W, MING X, WU Z, et al. A rough TOPSIS approach for failure mode and effects analysis in uncertain environments[J].
Quality & Reliability Engineering International, 2014, 30(4): 473-486.
|
| [8] |
张春勋. 改进的QFD与设计FMEA集成框架研究[J].
管理学报, 2009, 6(2): 207-212.
ZHANG Chunxun. The integrated framework research of improved QFD and DFMEA[J]. Management Journal, 2009, 6(2): 207-212. |
| [9] |
刘华文. 基于距离测度的模糊数排序[J].
山东大学学报:理学版, 2004, 39(2): 30-36.
LIU Huawen. The ranking fuzzy numbers based on distance measure[J]. Journal of Shandong University: Sciences Edition, 2004, 39(2): 30-36. |
| [10] |
和媛媛, 周德群, 巩在武. 三角模糊TOPSIS决策方法及其实验分析[J].
系统工程, 2010, 28(11): 95-103.
HE Yuanyuan, ZHOU Dequn, GONG Zaiwu. Machine experimental analysis of fuzzy TOPSIS decision method[J]. System Engineering, 2010, 28(11): 95-103. DOI: 10.3969/j.issn.1001-2362.2010.11.042. |
| [11] |
付学谦, 陈皓勇. 基于加权秩和比法的电能质量综合评估[J].
电力自动化设备, 2015, 35(1): 128-132.
FU Xueqian, CHEN Haoyong. Comprehensive evaluation of power quality based weighted RSR method[J]. Electric Power Automation Equipment, 2015, 35(1): 128-132. |
| [12] |
田凤调.秩和比法及其应用[M].北京:中国统计出版社, 2002.
|
 2016, Vol. 19
2016, Vol. 19