2. 青岛农业大学 经济与管理学院,山东 青岛 266000
2. School of Economics and Management, Qingdao Agricultural University, Qingdao 266000, China
随着国民经济和工业的不断发展,危险化学品的需求量逐年上升,其运输量与运输频次也日益增加。危险化学品由于自身的易燃、爆炸、毒害等特性,使得其运输与普通货物运输路径选择相比需要考虑的因素有较大的不同。普通货物运输主要考虑在运输需求量、运输时间等约束条件下选出一条运输成本最小化的运输路径,属于较典型的VRP问题;危险化学品运输的路径选择则还需考虑对运输沿线区域内人口、车辆、环境等方面的潜在危害,因为每辆危险化学品运输车辆都是一个流动的危险源,一旦事故发生,不仅附近区域的车辆及人员会受到损伤,由危险品爆炸、泄露、起火及扩散导致的二次事故将有可能引发更为严重的后果。因此科学、合理地选择安全且经济的运输路径,防范和降低路径风险,已成为危险化学品道路运输的主要研究重点。
对于危险化学品运输路径优化问题国内外许多学者进行了研究,合理的危险化学品运输路线必须考虑到控制和减少事故的发生,其优化选线标准需要综合考虑运输成本、运输风险、个人风险和社会风险等多个目标限制。选线方式可分为单目标选线与多目标选线。单目标选线确定某一优化目标然后进行道路优化选择。Miller-Hooks等[1]给出了以最小路径旅行时间为目标的有害品运输路径选线方法。Batta等[2]将危险化学品运输车辆与运输路径影响区内人口聚集中心之间的距离与影响人员总数的乘积作为选线标准。Lenoelli等[3]用单位运输成本和可能致死的生命价值来表示路径成本。多目标方面,邹宗峰等[4]建立了基于道路能力、风险、成本、交通状况和时间五大指标体系的混合时间窗条件下的多目标危险化学品运输路线优化模型,并给出了改进的多目标遗传算法,但其未考虑其他动态条件如时变、模糊不确定性等条件。Brainard等[5]采用成本最小化(成本为行程时间、道路等级、人口密度和事故率的函数)解决危险化学品配送问题。Wijeratne[6]提出了随机多目标最短路线算法搜索危险化学品运输网的非占优路线,最小化所有选线标准。周珣[7]提出了利用模糊综合评价和层次分析相结合的方法建立危险货物运输路线优化模型。Zografos等[8]提出了在考虑了时间参数情况下的最小化运输风险和最低运输成本的混合整数规划模型。
由现有的文献可知,对于危险化学品运输路径优化方面的研究包括时变动态网络下的单目标决策问题、不含时间窗的时变多目标决策问题等,并且在多目标优化选线问题的求解方式上,一般是对多目标赋予权重加权求和或将某些目标转化为约束条件,转化为单目标形式进行求解,前者权重的确定缺乏科学性,后者由于算法复杂性太高而有时无法求解。因此,本文将考虑与实际情况更吻合的存在时间窗约束的危险化学品道路运输时变多目标路径优化问题,建立数学模型并利用启发式算法求解,为危险化学品运输提供具有社会效益与经济效益的可行运输路径方案。
1 问题描述对于危险化学品运输路线选择问题,由于其涉及政府监管部门、运输企业、需求企业等多个参与对象,各对象从自身利益出发会产生不同的目标,一般来说,其目标涵盖了经济效益和安全运输两个方面,并且目标之间存在冲突难以同时达到最优。在运输过程中,由于交通流量、天气变化等因素的影响,事故的发生概率、道路人口密度、运输时间等路径属性往往随时间发生变化,因而运输成本和运输风险①具有动态、时变的特性。作为政府监管部门,在规划危险化学品运输路径时,可能会限制某些区域路段可服务于危险化学品运输车辆的时间段,以此降低运输对沿线区域带来的风险,所以还需要考虑节点的服务时间窗限制,在规定的时间段内才允许危险化学品运输车辆通行。这也引出了是否允许车辆在节点处等待以通过节点的问题,因为等待也会引起路段的运输成本和风险随时间改变,契合了运输网络的时变特性。
① 此处运输风险定义为事故率(数量级为10-8-10-6)与事故损失的函数,涉及具体事故幕景、影响范围、人口密度、致死率、事故损失计算方式等,对于其求解本文并不做推导。
2 模型建立与分析 2.1 模型建立G(N, A)为一个运输网络,其中N为网络中节点集合,可能为路段交叉点、重要设施位置点或人口中心点,0为起点,n+1为终点,A为边的集合。假设一辆危险化学品运输车辆需运输某类危险化学品从运输网络起点0至终点n+1,其可以在24 h内选择出发时间,但规定必须在时间T之前送达。已知每一个节点的允许服务时间窗为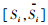
模型建立如下。
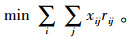
|
(1) |
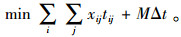
|
(2) |
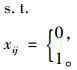
|
(3) |

|
(4) |
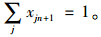
|
(5) |
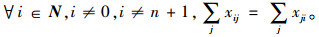
|
(6) |
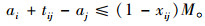
|
(7) |
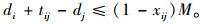
|
(8) |
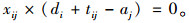
|
(9) |

|
(10) |

|
(11) |
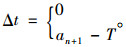
|
(12) |
其中M为一个极大数。
式(1)和(2)表示模型的多目标函数,即运输风险最小和运输时间最短,并且设定交货时间为硬时间窗,超过规定时间时运输时间无限大。式(3)~(6)表示网络中连接起点与终点的一条运输路径,xij为1表示节点i、j之间的路径被选中,为0则未被选中。式(7)与式(8)表示由于等待时间可能存在,所以到达节点i的时间加上路径ij上的行驶时间不会大于到达节点j的时间,离开节点j的时间加上路径ij上的行驶时间也不会大于离开节点j的时间。式(9)表示若路径ij被选中,则离开i的时间加上路径ij上的行驶时间等于到达j的时间;式(10)表示离开i的时间等于到达i的时间加上在i处的等待时间。式(11)表示离开节点i的时间必须满足节点i的服务时间窗要求。式(12)表示车辆的延误时间,若到达终点时间小于规定到达时间,则为0,否则为到达终点的时间减去事先规定的到达时间。
2.2 时变性分析实际运输时间和运输风险这两个属性的分布依赖于时间,本文对于其具体满足的分布给出如下定义。
1) 路径ij上所需的实际运输时间为
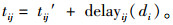
|
(13) |
其中tij′为路径ij上的理论运输时间,即路径ij里程值与行车速度的比值,delayij(di)为延迟时间。
定义1 某段路径实际运输时间可表示为路径(即理论运输时间)加上一个延迟时间,延迟时间服从指数分布,且其均值在一天的高峰时间段9点~17点为上述比值的20%,其余时间段为上述比值的10%[9-10],如式(13)所示。
2) 路径ij上的实际运输风险为

|
(14) |
其中riskij(di)为风险调节值。
定义2 危险化学品事故概率可分为正常期上午5点~9点、高峰期上午9点~下午17点、低峰期0点~5点及17点~24点4个时段。事故概率可以同样定义为由一个正常事故概率与一个时间有关的调节概率决定,假定该调节概率同样服从指数分布,在正常期其均值为正常事故概率的10%,高峰期和低峰期其期望值为正常事故概率的20%,对于高峰期应为正常事故概率加上与时间有关的调节概率,而低峰期则应为正常事故概率减去与时间有关的调节概率。假定路径事故损失值为定值,则路径损失风险主要取决于路径事故率,因此可以认为时变条件下,路径的风险值同样服从上述分布,如式(14)所示。
根据实际运输成本和运输风险的分布定义,每段路径的行驶延迟时间与风险调节值如表 1。
| 表 1 时间与风险调节函数 Tab. 1 Regulating functions of time and risk |
本文将基于蚁群算法进行求解,其基本思想是以信息素的浓度来指导蚂蚁进行节点路径的优化。通过蚂蚁在路径中的移动对各段弧的信息素进行增强,保证目标函数最小的路径对应的信息素浓度较高,使接下来越来越多的蚂蚁选择该条路径,最终得到较好的结果。
由于运输时间和运输风险具有不同的量纲,首先需对数据归一化,最后对结果进行还原。两者归一化因子设为: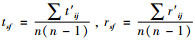
1) 在路径遍历搜索前,网络中每段路径拥有一个初始信息量,设为τij(t0),同时确定蚂蚁总数m及起点、终点。
2) 路径选择。
若第k只蚂蚁位于节点i,在选择下一条路径时,根据其可选择路径上的信息量τij(t)及路径的启发信息ηij(t)来计算状态转移概率:
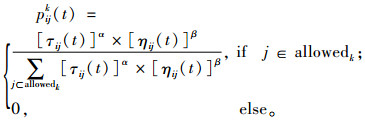
|
allowedk为蚂蚁k的可行节点集,其元素满足j∉tabuk,同时路径ij是通路;α为信息启发式因子,β为期望启发式因子,启发函数ηij设置为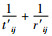
3) 目标函数计算。
对于到达终点的蚂蚁k,保存其所选择的路径及其在各节点的到达时间、等待时间及离开时间,并依此确定相应的目标函数值f1k、f2k(分别表示路径风险、运输时间)。
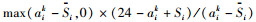
4) 路径信息素更新。
所有蚂蚁完成一次遍历时,路径的信息素按τij(t+1)=(1-ρ)×τij(t)+Δτij(t)更新,ρ为信息素蒸发系数,取值范围[0, 1],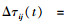
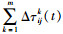
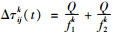
5) 非劣解筛选。
由于原问题为多目标优化问题,在大多数情况下,同时满足运输成本和风险成本达到最小值的路径几乎是不存在的,所以最后还需对蚁群选择的路径进行非劣排序,获得最大程度上满足以上两个目标的“次优”可行路径,即帕累托最优解集。对于非劣解的筛选按如下原则。
假设路径选线目标有s个,分别为{u1, u2, …, us}。设g、q为运输网络中由起点至终点的两条可行路径,则其路径属性分别为{u1(g), u2(g), …, us(g)}和{u1(q), u2(q), us(q)}。
1) 若对∀1≤l≤s,目标ul(g)≤ul(q)均成立,且∃1≤l≤s使得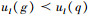
2) 若运输网络中不存在一条由起点至终点的可行路径r能够满足对∀1≤l≤s,目标ul(r)≤ul(g)均成立,则路径g为帕累托解。
3) 帕累托解集为帕累托最优解的集合。
经过最终筛选的解即为原问题的帕累托解。
4 算例结果及分析为了验证本文设计的算法对解决危险化学品运输路径选择问题的适用性及有效性,本文对文献[11]的案例数据进行仿真实验。
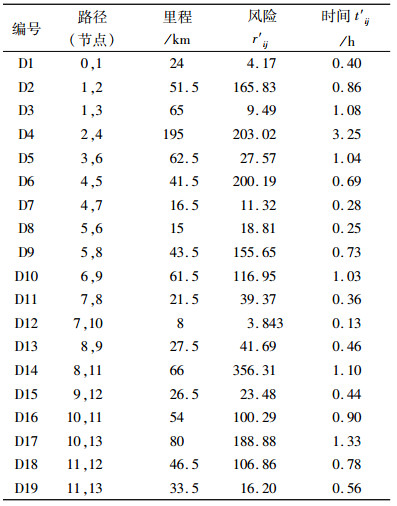
4.1 算例数据运输网络如图 1所示,有10 t液氯需要通过槽罐车由节点0运至节点13,各路径属性值如表 2。
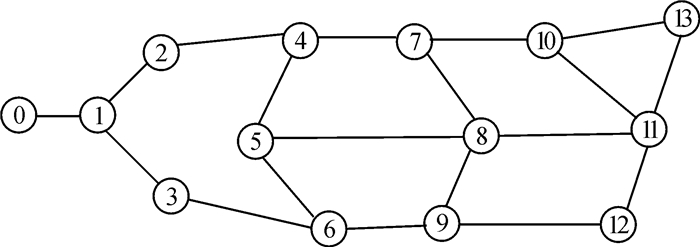
|
图 1 运输网络 Fig. 1 Transportation network |
| 表 2 路径属性表(未归一化) Tab. 2 Roads' attributes |
节点的允许服务时间窗如表 3所示,如节点5只允许车辆在9~20点通过。未标明的节点表示无服务时间窗限制,24 h内都允许通过。
| 表 3 节点服务时间窗 Tab. 3 Nodes' service time window |
假设要求达到时间为36,即第二天12点,初始化各参数,设置Gmax=50,m=200,α=2,β=0.2,ρ=0.05,Q=5,调用MATLAB编写的算法程序得到以下结果。
1) 指定出发时刻为0~23点中任一整点时刻,可求得始点至终点之间帕累托解集,如表 4所示。
| 表 4 帕累托解集1 Tab. 4 Pareto solution 1 |
表中4条路径为帕累托最优解集,决策者可依据此结果进行路径选择。可以看出,路径1、2运输风险与时间一致,但是路径1相比于路径2,出发时间提前1 h,等待时间增加1 h,到达时间则相同,可以推断是由于节点服务时间窗的限制导致路径1在某节点处增加了等待时间。路径3、4相比于路径1、2,虽然运输时间减少,但运输风险有所提升,同时由于出发时间及节点顺序的变化使得运输车辆较好地满足了节点服务时间窗限制,等待时间为0。
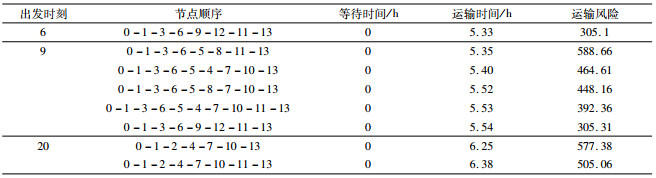
2) 指定出发时刻分别为6、9和20,得帕累托解集如表 5。
| 表 5 帕累托解集2 Tab. 5 Pareto solution 2 |
表 5说表明不同时间点出发获得的帕累托最优解个数有较大差别,如t=6出发只有一个非劣解,说明t=6出发可选路径较少,应避开此类时间点;t=9出发则有5个非劣解,可选路径较多。决策者可根据不同出发时间点的运输结果制定运输车辆的出发时间表,也可根据求得的帕累托最优解的具体路线结合实际问题和决策偏好作出最合适的决策。
3) 指定出发时刻为5点,利用算法求解下述3种情形下的运输路径帕累托解集情况如表 6所示。
| 表 6 帕累托解集3 Tab. 6 Pareto solution 3 |
情形1:存在服务时间窗约束,允许车辆在节点处等待。
情形2:存在服务时间窗约束,不允许车辆在节点处等待。
情形3:不存在服务时间窗约束,车辆无需在节点处等待。
情形1的解是情形2的解的非支配解,强制运输车辆必须满足节点服务窗限制且节点处不允许停留等待时,可选运输路径发生改变,偏向于选择没有服务时间窗限制的节点,导致运输时间与风险明显增加。情形1与情形3的解的路径顺序一致,但情形1由于允许在存在服务时间窗限制的节点处停留,使得运输车辆可以通过等待来改变通过路径的时间,进而降低路径的运输风险。对于危险化学品监管部门,可以通过合理规划各路径的服务时间窗及允许停留等待的节点,达到调节各路径运输时间及风险、影响决策者路径选择的目的。
5 小结危险化学品道路运输作为异于一般物品运输的问题,引起了政府、大众和学者的诸多关注。本文研究了带时间窗的时变多目标危险化学品运输路径选线问题,在运输时间及运输风险的多目标基础上,考虑运输时间与风险损失的时变性,并引入节点允许服务时间窗及是否允许车辆等待的条件。文章通过使用Matlab编写程序实现蚁群算法,给出运输路线的帕累托最优路径集求解算法。算例的仿真实验结果表明:1)算法可以给出相应的帕累托最优解集,为车辆行驶路径的选择提供决策支持;2)根据不同出发时刻的运输结果,运输企业可制定车辆的出发时刻表,决策者可结合实际问题和决策偏好作出最合适的决策;3)监管部门可通过合理规划各路径的服务时间窗及允许停留等待的节点来调节各路径运输时间及风险。总的来说,通过此算法可以获得时变随机条件下危险化学品运输帕累托优化路径集,为路径决策者根据自身的情况选择合适的出发时间和路径奠定了基础,但由于时变随机网络条件下以上算法的计算复杂性非常高,因此其对现实中对大型复杂道路网络下的应用尚需要进一步研究。
| [1] |
MILLER-HOOKS E, MAHMASSANI H S. Least expected time paths in stochastic, time-varying transportation networks[J].
Transportation Science, 2000, 34(2): 198-215.
DOI: 10.1287/trsc.34.2.198.12304. |
| [2] |
BATTA R, CHIU S S. Optimal obnoxious paths on a network: transportation of hazardous materials[J].
Operational Researeh, 1988, 36(1): 84-92.
|
| [3] |
LEONELLI P, BONVICINI S, SPADONI G. Hazardous materials transportation: a risk- analysis-based routing methodology[J].
Journal of Hazardous Materials, 2000, 71(1): 283-300.
|
| [4] |
邹宗峰, 张保全. 带混合时间窗的多目标危险化学品运输路径优化[J].
中国安全科学学报, 2012(4): 83-89.
ZHOU Zongfeng, ZHANG Baoquan. Path optimization on dangerous chemicals transport with mixed time window of multi-objective[J]. Chinese Journal of Safety Science, 2012(4): 83-89. |
| [5] |
BRAINARD J, LOVETT A, PARFITT J. Assessing hazardous waste transport risks using a GIS[J].
Geographical Information Systems, 1996, 10(7): 831-850.
DOI: 10.1080/02693799608902112. |
| [6] |
WIJERATNE A B. Routing and scheduling decisions in the management of hazardous material shipments[D]. NY: Cornell University, 1990.
|
| [7] |
周珣. 基于道路危险货物运输安全的路线优化研究[D]. 西安: 长安大学, 2004.
ZHOU Xun. Route optimization research based on hazmat transportation safety[D]. Xi'an: Chang'an University. |
| [8] |
ZOGRAFOS K G, ANDROUTSOPOULOS K N. A heuristic algorithm for solving hazardous materials distribution problems[J].
European Journal of Operational Research, 2004, 152(2): 507-519.
DOI: 10.1016/S0377-2217(03)00041-9. |
| [9] |
KULKARNI V G. Shortest paths in networks with exponentially distributed arc lengths[J].
Networks, 1986, 16(3): 255-274.
DOI: 10.1002/(ISSN)1097-0037. |
| [10] |
任福田, 刘小明.交通工程学[M]. 2版.北京:人民交通出版社, 2008.
|
| [11] |
王旭磊. 危险化学品道路运输风险分析与路线选择研究[D]. 上海: 上海大学, 2012.
WANG Xulei. Hazardous material road transportation risk analysis and path selection study[D]. Shanghai: Shanghai University, 2012. |
 2016, Vol. 19
2016, Vol. 19