电动汽车因具有节能环保等优点得到了政府的大力推广支持,但售价昂贵、维护成本高等劣势使其推广销售受阻[1-3]。租赁模式可有效解决电动汽车推广难题,不仅能使顾客无需承担高昂的采购和维护成本,消除使用顾虑,还能使生产商实现制造和服务的绑定,增加利润。鼓励探索租赁等商业模式也被列入政府制定的支持节能与新能源汽车产业发展规划中。按时间收费作为电动汽车租赁的一种主要收费模式[4],已被租赁商尝试采用,该模式指租赁商根据顾客租赁时间时段长短收取租赁费。根据电动汽车特征、租赁服务系统及顾客排队等多种复杂因素进行利润决策是出租商面临的难题,因此,对电动汽车租赁的按时间收费模式进行利润建模和优化分析,具有重要的理论和实践意义。
按时间收费方面,Chhabra等[5]基于马尔科夫决策理论建立按时间收费利润模型;Fruchter等[6]基于动态定价理论建立按时间收费制的瞬时收入模型;Lambrecht等[7]基于顾客行为特征建立按时间收费利润模型并分析其对收入的影响。但在建模时只以单一顾客为研究对象,未考虑顾客群体特征,或假设单位时间内前来的顾客数量可以无限增加,而实际中顾客到达率会被有限的市场规模等因素限制不能无限制增加。Madden等[8]基于动态需求理论建立考虑网络影响时按时间收费模式下用户的服务价值模型;McCabe[9]建立了考虑价格分歧时按时间收费模式下用户的服务价值模型;Issman等[10]建立按时间收费值下顾客价值模型并分析顾客特征对平衡状态时的临界价值影响。但在建模时均假设所有潜在顾客都会采用服务,不符合实际情况中某些顾客会因感知价值过低而不采纳该服务的特征,或未定量化描述选择服务的顾客具有的感知价值特征。Cachon等[11]基于排队论建立面向普通服务系统的按时间收费利润模型;Bitran等[12]运用排队论建立按时间收费利润模型并分析顾客在单一和群体状态下的服务选择特征;Tong等[13]基于排队论建立了面向自行决断服务的按时间收费收入模型并计算相应的服务绩效指标。这些文献展示了按时间收费服务系统的自然排队特征,但未考虑服务运营成本或成本针对普通服务系统。在成本方面,本文主要考虑与电动汽车行驶运行特征密切相关的维修成本,不考虑其他相关性很小的成本如管理或购置成本等,但有关电动汽车维修成本模型方面的研究,仅针对汽车或电池单方面研究,现存的车辆维修成本建模研究大多只针对汽车[14-16],不包含电池的特性,或只研究电池维护成本[17],不包含电动汽车行驶里程等特征。利润由服务系统、顾客排队、维修成本相关的多种因素综合决定,寻求最优利润是一个复杂的多因子数值优化问题。遗传算法[18]、模拟退火算法[19]、响应曲面法[20]等方法可用于解决多因子数值优化问题,然而只能基于大量试验数据寻求优化目标值,系统推理能力差且耗费成本高。在需同时兼顾盈利和效率的租赁商业环境中,耗费更少的人力、物力和时间获得优良结果显得尤为重要,试验设计法可通过较少的试验次数寻求到优良目标值,有很强的系统推理能力和较低的决策成本[21]。但传统试验设计法中,多依靠增加因素区间内取值个数来寻求更优的目标值,存在因为水平取值选取方向性不强造成优化效率低的问题,容易出现虽然因素取值个数大量增加,但所得目标值的优化程度却很弱的现象。
本文假设了顾客感知服务价值的分布函数和取值区间,用来表示选择服务顾客占总体顾客数的比例,再结合顾客最大到达率、电池损耗系数、行驶里程等参数,研究构建了包含顾客到达率瓶颈、顾客依据感知价值选择服务的特征及电动汽车特性的利润模型,使模型更贴近现实。为提升利润优化效率,提出改进试验设计法,求解利润模型,比传统试验设计法得出显著更优结果,再采用极差分析法确定参数对利润的影响程度,最终达到高效低成本地优化利润的目标,为电动汽车出租商优化按时间收费模式的利润提供决策依据。
1 利润模型电动汽车租赁的按时间收费模式利润模型包括电动汽车的维修成本模型和租赁收入模型两部分。
1.1 维修成本模型设某时段内,电动汽车的损坏次数η服从泊松分布[16],考虑到损坏次数与行驶里程有正相关关系[14],设泊松分布的系数为rs0S,表示平均损坏次数,s0S为行驶里程,r>0,表示平均损坏次数与行驶里程之间关联度的常数。电池损耗系数为C,与电池充电能力有关[22],电池充电能力越差,电池损耗系数越大。故电池损耗系数为C的电动汽车行驶s0S里程,损坏次数为η的损坏概率为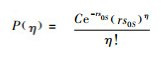
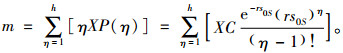
|
(1) |
设当顾客认为按时间收费模式租车带来的服务价值V不低于临界值VS时才会租车。VS可表示为
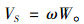
|
(2) |
式(2)中,服务价值临界值VS等于顾客租车过程中耗费的等待成本ωW。ω为每位顾客单位时间内花费的等待成本;W为顾客等待时间,指顾客从开始申请租车到成功取到车期间花费的时间。为了更清晰地描述选择服务的顾客特征,选取有适用性强、队列状况不确定因素少、可控性强等优点的M/M/1排队模型[11, 13]用于后续租赁服务建模分析过程,则由标准排队理论知,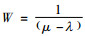
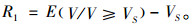
|
(3) |
式(3)中,E(V/V≥VS)是选择按时间收费模式租车的顾客认为其带来服务价值V的期望值,V与电动汽车及按时间收费模式的特点有关,如品牌、马力、充电特性、收费时段等[23]。单位时间内出租商从所有顾客处获得的收入RS1为
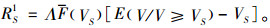
|
(4) |
由式(1)和式(4),可得出租商单位时间内获得的利润
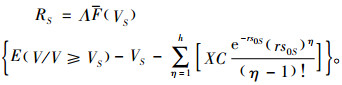
|
(5) |
设电动汽车租赁市场中的潜在客户均匀且独立,服务价值V满足均匀分布[11],即相等长度服务价值区间内的顾客数相同,用V~U[0, V]表示,可得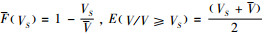
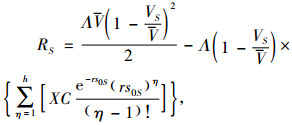
|
(6) |
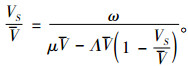
|
(7) |
式(7)中,由μ>λ知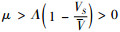
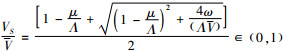
将式(7)代入式(6)得
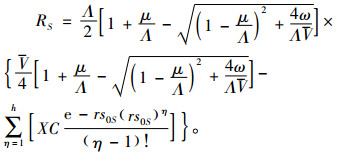
|
(8) |
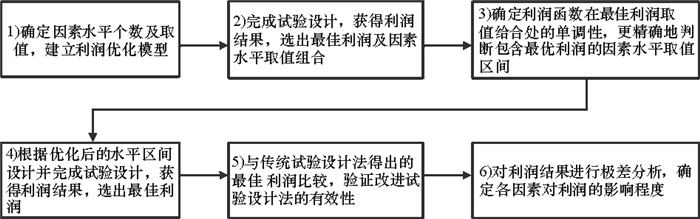
利润RS与电动汽车(r、s0S、h、C、X)、租赁服务系统(ω、μ)及顾客排队(Λ、V)等多方面满足复杂约束的参数有关。试验设计法系统推理能力强且成本低,可低成本高效地优化RS并确定因素对其影响程度,但多依靠增加因素区间内取值个数来寻求更优的目标值,因素水平选取方向性不强,优化效率较低。为解决该问题,先采用传统试验设计法求出最佳利润及取值组合,确定利润函数在最佳利润取值组合处的单调性,进而更精确地判断包含最优利润的因素水平取值区间,基于精确化后的因素取值区间,保持因素水平数不变,采用试验设计法再次优化利润,可获取显著更优的利润结果,对试验结果进行极差分析确定因素对利润的影响程度。模型求解步骤如图 1所示。
|
图 1 改进试验设计法优化利润的步骤 Fig. 1 Steps of Modified design-of-experiments method |
1) 确定因素的水平个数及取值,建立利润优化模型。由建模部分参数含义知利润相关因子ω、μ、r、s0S、h、Λ、V、X、C相互独立,设每个因子分别有nω、nμ、nr、nS、nh、nΛ、nV、nX、nC个水平,从每个因子中各取一个水平,共构成nωnμnrnSnhnΛnVnXnC个水平组合,由式(8)可求得对应的利润试验结果RS。利润优化模型表示为
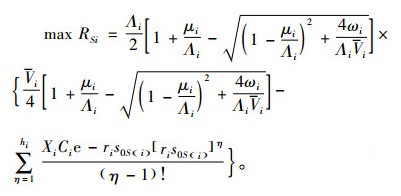
|
(9) |
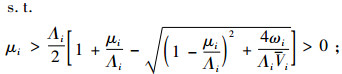
|
(10) |
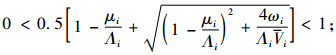
|
(11) |
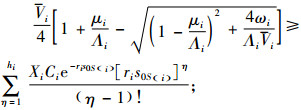
|
(12) |
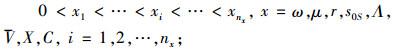
|
(13) |
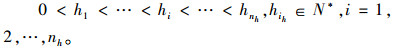
|
(14) |
式(9)为最大化利润的目标函数,RSi为各因子分别取第i水平(ωi、μi、ri、s0S(i)、hi、Λi、Vi、Xi、Ci)时得到的利润结果。式(10)~(14)为约束条件,N*表示正整数集,式(10)由式(7)成立的条件μ>λ得出,式(11)由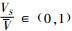
2) 完成试验设计,获得利润结果,选出最佳利润及水平取值组合。由式(13)知8个因素的水平范围为[x1, xnx],水平数为nx且各因子相互独立,选择无交互作用水平不等的单指标(以利润最大为目标)试验设计表LM(nω1nμ1nr1nS1nΛ1nV1nX1nC1),M为试验次数,上标1表示因素占的列数,进行试验分析。不同因素水平组合对应的试验结果如表 1所示。
| 表 1 试验条件及结果表 Tab. 1 Experiment conditions and results |
表 1中,j指代任意一次试验,yj表示第j次试验中因素水平取值组合,所得利润结果为RSj(yj)=RSj(ωj, μj, rj, s0Sj, Λj, Vj, Xj, Cj),可由该次试验中各因素水平取值及式(8)得出,设最优利润在第l次试验取得,为RSl(yl)=max RSj(yj),对应因素取值为yl=ωl, μl, rl, s0Sl, Λl, Vl, Xl, Cl。kxj表示因素x的第j个水平值xj在所有试验(每列)中出现的次数。
3) 确定利润函数在最佳取值组合处的单调性,更加精确地判断取得最优利润的各因素水平取值区间,增强水平选择的方向性。为更精确地确定最优利润存在的水平区间,需确定RS的函数极值点个数及单调性,则需以各参数为自变量对RS求一阶导数得
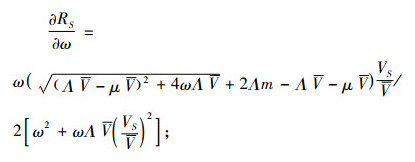
|
(15) |
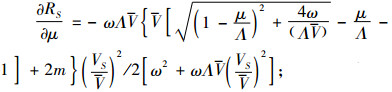
|
(16) |
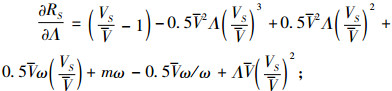
|
(17) |
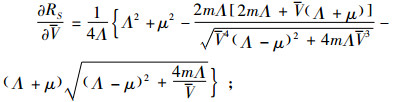
|
(18) |
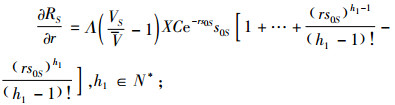
|
(19) |
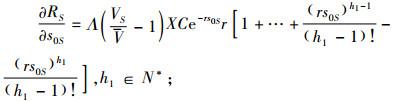
|
(20) |
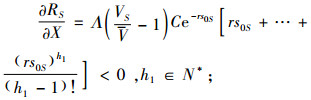
|
(21) |
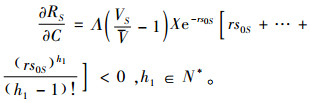
|
(22) |
式(15)~(17),(19)~(22)为联立式(6)、(7)求导得出,式(18)为对式(8)求导得出。
式(15)中,令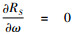
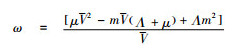
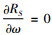
式(16)中,令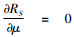
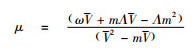
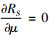
式(17)中令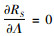
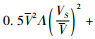
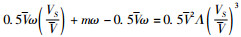
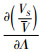
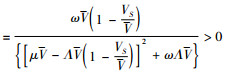
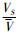
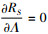
式(18)中令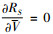
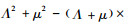
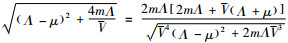
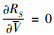
式(19)中,令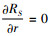
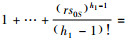
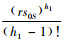
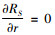
同理,可知式(20)中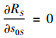
式(21)、(22)中,由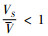
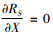
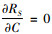
综上,RS有唯一极值点(类凸或类凹)或无极值点(单调)。
由式(13)知因素x的原始水平范围为[x1, xnx],设优化后的水平范围为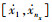
| 表 2 优化后的因素水平取值区间 Tab. 2 Optimized value ranges of factor levels |
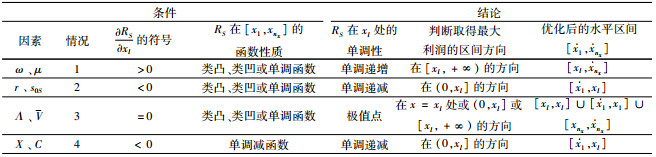
表 2中,根据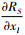
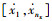
情况1~3针对因素ω、μ、r、s0S、h、Λ及V。以因素ω为例说明,其他因素μ、r、s0S、Λ、V分析原理类似。
情况1:由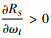
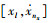
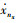
情况2:由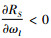
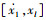
情况3:由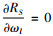
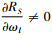
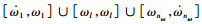
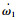
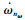
情况4:针对因素X及C,由式(21)、(22)知,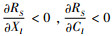
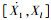
4) 根据优化后的水平区间,重新设计并完成试验设计,获得利润结果,选出最佳利润。根据优化后的水平区间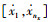
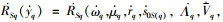
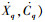
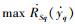
5) 与传统试验设计法得出的最佳利润比较,验证改进试验设计法的有效性。计算优化前后得出利润的变化率
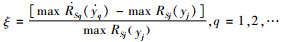
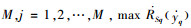
6) 对利润结果作极差分析,确定各因素对利润的影响程度。极差
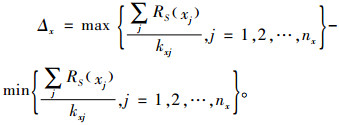
|
(23) |
式(23)中,Δx为各因素x的不同水平(xj, j=1, 2, …, nx)下对应的利润结果极值,Δx越大,表示因素x对利润的影响越大,先对试验表每列中因素x同一水平xj下的试验结果RS(xj)求均值,再寻找均值中的最大值和最小值,二者之差为Δx。
3 案例分析通过用实例验证改进后试验设计法优化利润的有效性并确定因素对利润的影响程度,辅助出租商调整现有的因素取值取得更大利润,当预算有限时可做到有选择性地调整影响程度更大的因素。
1) 确定因素的水平个数及取值。设出租商经过对电动汽车租赁服务系统的实地调研观测,得出的利润相关因素取值如表 3所示。
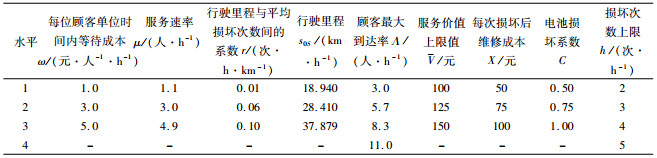
| 表 3 优化前的因素水平表 Tab. 3 Value ranges of factor levels before optimization |
表 3中,s0S是指1 h研究时段的行驶里程。确定s0S范围时,假设顾客年行驶里程范围为[500 000, 100 000]km,每月平均使用天数为22,每天使用时数为10,不再展示获取参数范围的具体过程,实际可经过市场调查及服务系统评估确定。由第3部分知,为使利润最大,取h=2次/h,将ω、μ、r、s0S、Λ、V、X和C作为试验设计的8个因素。
2) 完成试验设计,获得利润结果,选出最佳利润。运用Minitab软件设计L8700(31×47)全因子试验,获取的最佳利润为RS=287.5元/h,对应因素取值分别为:ω=1元/(人·h),μ=4.9人/h,r=0.01次·h·km-1,s0S=18.940km/h, Λ=5.7人/h, V=150元,X=50元,C=0.5。
3) 为使出租商进一步优化利润,需确定因素水平优化方向。根据表 2求利润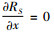
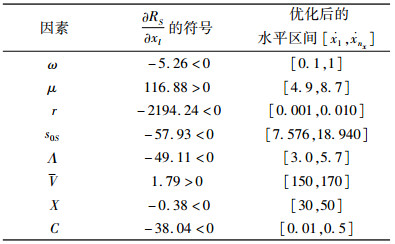
| 表 4 优化后的因素水平取值区间 Tab. 4 Value ranges of factor level after optimization |
将表 4中参数值代入式(16)~(23)中,得出利润一阶导数在最优利润点处的符号,进而确定利润RS在该点处的单调性。由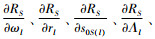
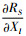
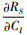
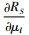
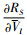
4) 确定优化水平区间后的试验设计因素水平表,如表 5所示。
| 表 5 优化后的因素水平表 Tab. 5 Factor level table after optimization |
5) 根据表 5中优化水平区间后的水平取值,完成试验设计,获得利润结果。所得的最大利润结果为ṘS=484.3元/h,对应因素取值分别为: 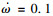
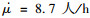
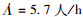
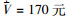
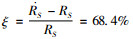
6) 确定因素对利润影响的大小,寻找影响利润的关键因素。通过对各因素不同水平下的利润结果作极差分析确定各因素对利润的影响程度,如表 6所示。
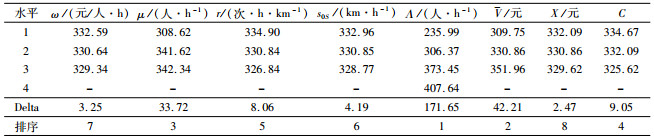
| 表 6 各因素对利润的影响排序 Tab. 6 Influential rankings of factors on profit |
表 6中可看出各因素取不同水平下对应的利润值及极差Delta,Delta越大表示因素对利润影响程度越大,可知Λ、V、μ、C、r、s0S、ω及X对利润的影响逐渐减小。当提高利润的预算有限时,出租商可选择改变对利润影响较大的因素,如增强按时间租赁收费模式的营销力度,增加潜在顾客数,进而提升顾客最大到达率Λ,提高租赁服务质量及顾客对出租电动汽车的感知价值等,进而增加服务价值上限V,完善服务设施进而增加服务速率μ,选择电池损耗系数C低(电池老化度低)的车出租等。
4 结论建立并优化电动汽车租赁收费利润模型是辅助出租商作利润决策的有效途径。提出了面向电动汽车租赁的按时间收费利润模型,将顾客到达率瓶颈、顾客依据感知服务价值选择服务的特征及电动汽车特性考虑进入模型构建过程,采用改进试验设计法优化利润,极差分析法确定各因素对利润的影响程度。通过算例分析可知改进后试验设计法所得利润值比改进前所得利润值显著更优,并得出因素的利润影响度排序,为出租商预测并有选择性地根据影响度大的因素优化利润提供决策依据。
| [1] |
KIM D, KO J, PARK Y. Factors affecting electric vehicle sharing program participants' attitudes about car ownership and program participation[J].
Transportation Research Part D: Transport and Environment, 2015, 36: 96-106.
DOI: 10.1016/j.trd.2015.02.009. |
| [2] |
KRAUSE R M, CARLEY S R, LANE B W, et al. Perception and reality: public knowledge of plug-in electric vehicles in 21 U.S. cities[J].
Energy Policy, 2013, 63: 433-440.
DOI: 10.1016/j.enpol.2013.09.018. |
| [3] |
MAK H Y, RONG Y, SHEN Z J M. Infrastructure planning for electric vehicles with battery swapping[J].
Management Science, 2013, 59(7): 1557-1575.
DOI: 10.1287/mnsc.1120.1672. |
| [4] |
WILLIAMS A. Product service systems in the automobile industry: contribution to system innovation[J].
Journal of Cleaner Production, 2007, 15(11): 1093-1103.
|
| [5] |
CHHABRA M, DAS S, SARNE D. Expert-mediated sequential search[J].
European Journal of Operational Research, 2014, 234(3): 861-873.
DOI: 10.1016/j.ejor.2013.10.033. |
| [6] |
FRUCHTER G E, SIGUÈS P. Dynamic pricing for subscription services[J].
Journal of Economic Dynamics and Control, 2013, 37(11): 2180-2194.
DOI: 10.1016/j.jedc.2013.05.003. |
| [7] |
LAMBRECHT A, SEIM K, VILCASSIM N, et al. Price discrimination in service industries[J].
Marketing Letters, 2012, 23(2): 423-438.
DOI: 10.1007/s11002-012-9187-0. |
| [8] |
MADDEN G, COBLE-NEAL G, DALZELL B. A dynamic model of mobile telephony subscription incorporating a network effect[J].
Telecommunications Policy, 2004, 28(2): 133-144.
DOI: 10.1016/j.telpol.2003.12.002. |
| [9] |
MCCABE M J. Information goods and endogenous pricing strategies: the case of academic journals[J].
Economics Bulletin, 2004, 12(10): 1-11.
|
| [10] |
ISSMAN E, SHY O. Pricing of library subscriptions with applications to scientific journals[J].
Journal of Economics and Business, 2003, 55(2): 197-218.
DOI: 10.1016/S0148-6195(02)00136-4. |
| [11] |
CACHON G P, FELDMAN P. Pricing services subject to congestion: charge per-use fees or sell subscriptions[J].
M & SOM-Manufacturing & Service Operations Management, 2011, 13(2): 244-260.
|
| [12] |
BITRAN G R, OLIVEIRA P R, SCHILKRUTA. Managing customer relationships through price and service quality[R/OL]. (2008-09-09). http://dx.doi.org/10.2139/ssrn.1264933.
|
| [13] |
TONG C, RAJAGOPALAN S. Pricing and operational performance in discretionary services[J].
Production and Operations Management, 2014, 23(4): 689-703.
DOI: 10.1111/poms.2014.23.issue-4. |
| [14] |
KRIVTSOV V, FRANKSTEIN M. Nonparametric estimation of marginal failure distributions from dually censored automotive data[C/OL]. (2004-01-26). http://dx.doi.org/10.1109/RAMS.2004.1285428.
|
| [15] |
RAI B, SINGH N. A modeling framework for assessing the impact of new time/mileage warranty limits on the number and cost of automotive warranty claims[J].
Reliability Engineering & System Safety, 2005, 88(2): 157-169.
|
| [16] |
AKSEZER C S. Failure analysis and warranty modeling of used cars[J].
Engineering Failure Analysis, 2011, 18(6): 1520-1526.
DOI: 10.1016/j.engfailanal.2011.05.009. |
| [17] |
HAN Y, WANG J, ZHAO Q, et al. An optimal operating strategy for battery life cycle costs in electric vehicles[J/OL]. (2014-03-11). http://dx.doi.org/10.1155/2014/305905.
|
| [18] |
THAKUR M, MEGHWANI S S, JALOTA H. A modified real coded genetic algorithm for constrained optimization[J].
Applied Mathematics and Computation, 2014, 235: 292-317.
DOI: 10.1016/j.amc.2014.02.093. |
| [19] |
NEDIC V, CVETANOVIC S, DESPOTOVIC D, et al. Data mining with various optimization methods[J].
Expert Systems with Applications, 2014, 41(8): 3993-3999.
DOI: 10.1016/j.eswa.2013.12.025. |
| [20] |
NEŞELI S, YALDŞZ S, TVRKEŞ E. Optimization of tool geometry parameters for turning operations based on the response surface methodology[J].
Measurement, 2011, 44(3): 580-587.
DOI: 10.1016/j.measurement.2010.11.018. |
| [21] |
LI Z, LI Z, NGUGEN T T, et al. Orthogonal chemical reaction optimization algorithm for global numerical optimization problems[J].
Expert Systems with Applications, 2015, 42(6): 3242-3252.
DOI: 10.1016/j.eswa.2014.11.045. |
| [22] |
KIM T, QIAO A W. A hybrid battery model capable of capturing dynamic circuit characteristics and nonlinear capacity effects[J].
Energy Conversion, IEEE Transactions on, 2011, 26(4): 1172-1180.
DOI: 10.1109/TEC.2011.2167014. |
| [23] |
MIAO R, XU F, ZHANG K, et al. Development of a multi-scale model for customer perceived value of electric vehicles[J].
International Journal of Production Research, 2014, 52(16): 4820-4834.
DOI: 10.1080/00207543.2014.890757. |
 2016, Vol. 19
2016, Vol. 19