2. 重庆理工大学 管理学院,重庆 400054
2. College of Management, Chongqing University of Technology, Chongqing 400054, China
以决策主体“纯粹自利”为假设条件的供应链管理研究没有考虑供应链主体的行为和心理特征,从而不能真实地反映现实中的供应链管理行为[1]。行为经济学研究表明,在自利关切之外,人们还存在其他行为心理特征,这些心理特征对人们的决策行为产生重要影响,使其偏离“纯粹自利”假设下的决策结果[2]。公平关切就是一种客观存在的非常重要的心理特征。具有公平关切的人们不仅关注自身的利润,还关注利润分配的公平性[3]。Katok等[4]通过实验分析了不公平规避、有界理性和不完全信息3种能够造成供应链低效率化的因素,发现不公平规避对零售商的决策行为产生的影响最大。可见,决策者的公平关切心理特征是客观存在的影响供应链运作的重要因素。
Hopp[5]认为对决策者行为心理特征的关注很可能成为管理科学研究的新趋势。近些年,一些国内外学者已经开始尝试将决策者的公平关切纳入供应链运作的研究中。通过对现有研究文献的梳理,发现学者们在建立决策者公平关切效用模型时,主要存在两种判断公平与否的参考点:1)以对方利润为参考的绝对公平关切;2)以决策双方Nash讨价还价均衡解为公平参考解的相对公平关切。大多数文献假设决策者是绝对公平关切的,以此研究公平关切对供应链决策与协调的影响。Cui等[6]研究了决策者的公平关切对供应链契约协调性的影响,发现在一方或双方都具有公平关切下,供应商仍能够设计合适的批发价格契约协调供应链。Caliskan-Demirag等[7]对Cui等[6]的研究进行了扩展,指出与线性的需求函数相比,当只有零售商具有公平关切时,指数需求函数下供应链协调更为容易实现。马利军[8]指出零售商的公平关切能够提高其自身的讨价还价能力,从而获得更多的供应链利润。林强等[9]针对零售商的努力行为和公平关切,研究设计了能够实现双渠道供应链协调的改进回购契约。另外,成克河等[10]探讨了公平关切对渠道成员最优定价的影响。
在现实生活中,公平具有相对性。在一个供应链中,决策双方的实力与贡献会影响利益分配的结果。基于此,部分学者尝试以决策双方Nash讨价还价均衡解为公平参考解进行相关研究。杜少甫等[11]研究表明零售商存在相对公平关切时,其最优决策趋于保守。张克勇等[12]基于零售商的相对公平关切行为,研究了闭环供应链的差别定价策略,指出零售商的讨价还价公平关切行为能够为其获得更多的供应链利润。Shi等[13]建立了由一个供应商和两个同质的零售商组成的供应链模型,研究决策者的订货量与定价决策。覃燕红等[14]基于Stackelberg博弈模型研究表明,无论是否考虑决策主体的公平关切,经典的回购契约都不能实现供应链协调。
现有的考虑公平关切的供应链研究文献大多数考虑决策主体的绝对公平关切。虽然有部分学者指出绝对公平不符合实际,转而考虑决策者的相对公平关切,但目前还没有学者对两种公平关切下的决策结果进行比较研究,以明确两种公平关切下决策者的策略选择与利润获取存在哪些不同之处。同时,大多数相关文献都集中于在报童模型背景下研究供应链的订货量决策以及契约协调问题,涉及到供应链定价决策的文献很少。基于此,本文尝试分别探讨绝对公平关切和相对公平关切对传统单零售渠道供应链定价决策以及利润的影响。一方面将两种公平关切下的定价策略与利润同供应链成员为公平中性时的定价策略与利润进行比较;另一方面,分析比较两种公平关切下的定价策略与利润,以丰富现有的理论研究并得到更加符合实际的管理启示。
1 模型描述考虑由一个制造商和一个零售商组成的两级供应链结构,制造商通过零售商只销售单一品种产品。双方在定价博弈时,假设价格决策的信息是对称的,制造商率先制定一个批发价格wB,然后零售商根据得到的批发价格信息确定零售价格pB。为了分析的简便,假设市场需求函数仅受零售商的零售价格的影响,即D(pB)=a-bpB,其中a为基本市场需求,b为价格影响系数且b>0;供应链中只有制造商存在单位生产成本c,除此之外不考虑其他任何成本。根据以上假设,可知零售商、制造商和供应链的利润函数分别为πBr=(pB-wB)D(pB),πBm=(wB-c)D(pB), πBt=(pB-c)D(pB)。上标r、m、t分别表示零售商、制造商和供应链整体;下标B表示公平中性的供应链模型,下文中下标R、N分别表示绝对公平关切情形、相对公平关切情形。
2 供应链成员为公平中性时的定价策略在产品定价时,制造商和零售商进行Stackelberg博弈。利用逆推法,零售商在第2阶段假设批发价格信息已知的情况下确定零售价格。易知,零售商利润函数关于pB的二阶导数以及制造商利润函数关于wB的二阶导数均小于0,所以零售商存在唯一最优的零售价格pB*且满足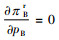
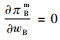

|
(1) |
本文假设零售商是公平关切的,制造商了解这一信息并予以关注。这就意味着零售商在制定价格决策时不仅考虑自己的实际收益,而且关注收益分配结果的公平与否,即零售商决策的目标是最大化其效用函数,而制造商在进行批发价格决策时也要考虑零售商的公平关切。
3.1 零售商为绝对公平关切情形在由制造商和零售商组成的两级供应链关系中,如果零售商的实力较小,往往只能获得少部分供应链利润。此时,零售商不情愿以实力或贡献来参与供应链的利润分配,而更愿意通过直接与制造商的利润进行比较来表达对公平的关切。采用参考点依赖的方式刻画零售商的公平关切效用函数,即零售商直接以制造商的利润作为己方利润的参考点,显示出零售商的绝对公平关切感知。在刻画该效用函数时,假设利润差异会带来效用的变化,即:零售商的利润与制造商的利润差距越大,零售商的效用损失就越大。学者们为了计算简便考虑,假设决策者面对同等利润和损失的敏感程度一样,即直线型[10-11]。引入参数λ(λ>0)作为零售商的公平关切系数,得到零售商的效用函数为
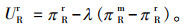
|
(2) |
命题1 零售商具有绝对公平关切时,零售商的最优零售价格pR*满足式(5),且等于其公平中性时的最优零售价格;制造商的最优批发价格wR*满足式(5),且小于零售商公平中性时其最优批发价格。
证明 零售商的效用函数关于pR的一阶和二阶导数为

|
易知零售商存在唯一最优的零售价格pR*,且满足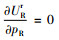
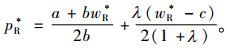
|
(3) |
制造商效用函数关于wR的一阶和二阶导数为
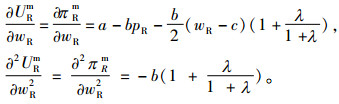
|
易知制造商存在唯一最优的批发价格wR*,且满足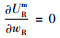
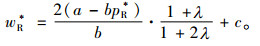
|
(4) |
联立式(3)和(4),可得双方Stackelberg博弈的均衡解为
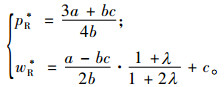
|
(5) |
对比式(1)与(5)易知,pR*=pB*;wR* < wB*。可见,当零售商具有绝对公平关切时,制造商关注零售商的公平关切并采取降低批发价格的行为,而零售商的价格决策保持不变,即与其公平关切程度无关。
3.2 零售商为相对公平关切情形如果在某条供应链中零售商的经营规模、实力和影响力都比较大,例如苏宁、国美电器,这样的零售商往往具有相对公平关切,常常要求制造商压低批发价格,从而使自身获得更多的供应链利润。假设决策双方Nash讨价还价模型的均衡解为


|
(6) |
命题2 零售商具有相对公平关切时,零售商的最优零售价格pN*满足式(9),且等于其公平中性时的最优零售价格;制造商的最优批发价格wN*满足式(9),且小于零售商公平中性时其最优批发价格。
证明 零售商的效用函数关于pN的一阶和二阶导数为

|
易知零售商存在唯一最优的零售价格pN*, 且满足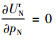

|
(7) |
制造商效用函数关于wN的一阶和二阶导数为
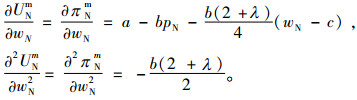
|
易知制造商存在唯一最优的批发价格wN*,且满足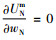
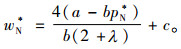
|
(8) |
联立式(8)和(9),可得双方Stackelberg博弈的均衡解为
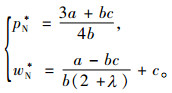
|
(9) |
对比式(1)与(9)易知,pN*=pB*;wN* < wB*。可见,当零售商具有相对公平关切时,制造商关注零售商的公平关切并采取降低批发价格的行为,而零售商的价格决策保持不变,即与其公平关切程度无关。
命题3 当0 < λ≤1时,有wR*≤wN*;当λ>1时,有wR*>wN*。
证明 比较式(5)与(9),有
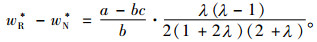
|
(10) |
易知,当0 < λ≤1时,有wR*≤wN*;当λ>1时,有wR*>wN*。在制造商主导的两级供应链中,制造商因实力和贡献较大而拥有较强的话语权,制造商以率先制定批发价格的方式占据供应链较多份额的利润。而当零售商具有公平关切行为特征时,制造商会降低其批发价格以维护渠道关系。命题1和命题2证明如此。当零售商的公平关切度较弱,即0 < λ < 1时,在考虑了双方的实力与贡献的相对公平关切下,制造商的批发让价幅度小于零售商纯粹以对方利润为参考点的绝对公平关切情形;而当零售商的公平关切程度较强,即λ>1时,零售商相对公平关切下,制造商的批发让价幅度大于零售商绝对公平关切情形。这就为制造商进行批发价格决策提供了参考依据。当零售商的公平关切程度较弱时,制造商不会选择在绝对公平关切模型下确定自己的批发价格,因为那样将毫无意义地损失自己的利润份额;而在零售商公平关切程度较强时,制造商可以权衡利弊,选择在何种公平关切模型下确定自己的批发价格。在绝对公平关切模型下,制造商可以制定较高一点的批发价格,从而保持更高的利润水平;在相对公平关切模型下,制造商的批发价格虽然低一些,但是从维护供应链合作关系角度来看对双方和整个供应链都是有好处的。
性质1 两种公平关切情形下,制造商的批发价格均随零售商公平关切程度的增大而减小。
证明 绝对公平关切下,wR*关于λ的一阶导数为

|
相对公平关切下,wN*关于λ的一阶导数为

|
不失一般性,有bc-a < 0,故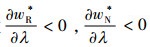
根据上文分析,可得零售商、制造商与供应链整体在不同公平关切情形下的利润表达式,如表 1。
| 表 1 不同公平关切情形下供应链成员的利润 Tab. 1 The profits of supply chain members under different situation of fairness concern |
表 1表明,零售商的公平关切不改变供应链整体的利润水平,但改变零售商与制造商之间的利润分配结果。也就是说,零售商的公平关切起到了一种利润分配机制的作用。在某条供应链上,无论哪一个决策方起到主导作用,只要主导者能够适当关注其他供应链上成员的公平关切行为,即使短期内会导致自身利润份额的减少,但从长期来看对维护供应链稳定、和谐和健康的合作关系有着积极作用。
命题4 零售商公平关切时,两种公平关切情形下,零售商获得的最优利润均大于其为公平中性的情形。当0 < λ < 1时,绝对公平关切情形下零售商的最优利润大于相对公平关切下的情形;当λ>1时,绝对公平关切下零售商的最优利润小于相对公平关切下的情形。而制造商的最优利润情况与零售商正好相反。
证明 易知
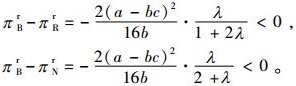
|
故有πBr < πRr、πBr < πNr;而
性质2 两种公平关切情形下,零售商的最优利润均随其公平关切程度的增大而增加;制造商的最优利润均随零售商公平关切程度的增大而减小。
证明 易知,绝对公平关切情形下,有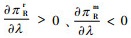

现有的考虑决策主体公平关切的供应链管理研究文献要么强调决策者的绝对公平关切,要么强调决策者的相对公平关切。针对这一事实,本文尝试分别从绝对公平关切和相对公平关切两种角度探讨零售商公平关切对供应链定价策略及利润的影响,并对两种公平关切情形下的决策结果进行比较分析。结果表明,考虑了零售商的公平关切后,制造商的最优批发价格小于零售商公平中性时的情形,零售商的最优零售价格保持不变,这就导致零售商将获得比其公平中性时更多的供应链利润。说明为了维护渠道公平,制造商宁愿选择批发让价,宁愿让出部分供应链利润给零售商,以应对零售商的公平关切行为。在两种公平关切情形下,制造商的最优批发价格和最优利润均随零售商公平关切程度的增大而减小,零售商的最优利润均随其公平关切程度的增大而增大。但是,受零售商公平关切程度的影响,两种公平关切情形下的制造商的定价策略以及供应链成员利润呈现明显的分段差异性。这些研究结果具有实际应用价值。比如,戴尔集团为了维护良好渠道关系,除了补偿供应商的全部物流成本,还让其成为戴尔的分销商,同时享有供货总额3%~5%的利润,戴尔的利他行为使戴尔电脑供应、生产、销售紧密结合,实现了战略合作伙伴关系和各个决策主体共赢的目标。至于制造商如何能够准确地判断零售商的公平关切程度,从而更好地进行批发价格决策,已超出了本文的研究范畴,需要制造商根据已知的信息和经验或者在与零售商多次博弈中做出判断。
本文在建模分析中,为了简化分析,假设市场需求是确定的线性结构,并假设供应链成员中只有制造商产生生产成本,不考虑其他各类成本,采用的公平关切效用函数也是较为简单的线性函数,并只考虑零售商的公平关切。实际上,供应链成员会发生生产成本、销售成本、库存成本、缺货成本等很多类别的成本,市场需求是不确定的,每个供应链成员都有可能具有公平关切。另外,本文假设信息是对称的,而实际上供应链成员之间的决策信息并不是完全透明的。因此,以后的相关研究将考虑更为复杂的供应链模型、不确定性市场需求、制造商的公平关切以及信息不对称等情形,以对现有研究进行进一步修正和完善。
| [1] |
GINO F, PISANO G. Toward a theory of behavioral operations[J].
Manufacturing Service Operations Management, 2008, 10(4): 676-691.
DOI: 10.1287/msom.1070.0205. |
| [2] |
LOCH C H, WU Y Z. Social preferences and supply chain performance: an experimental study[J].
Management Science, 2008, 54(11): 1835-1849.
DOI: 10.1287/mnsc.1080.0910. |
| [3] |
FEHR E, SCHMIDT K M. A theory of fairness, competition and cooperation[J].
Quarterly Journal of Economics, 1999, 114(3): 817-868.
DOI: 10.1162/003355399556151. |
| [4] |
KATOK E, PAVLOV V. Fairness in supply chain contracts: a laboratory study[J].
Journal of Operations Management, 2013, 31(3): 129-137.
DOI: 10.1016/j.jom.2013.01.001. |
| [5] |
HOPP W J. Fifty years of management science[J].
Management Science, 2004, 50(1): 1-7.
|
| [6] |
CUI T H, RAJU J S, ZHANG Z J. Fairness and channel coordination[J].
Management Science, 2007, 53(8): 1303-1314.
DOI: 10.1287/mnsc.1060.0697. |
| [7] |
CALISKAN-DEMIRAG O, CHEN Y F, LI J. Channel coordination under fairness concerns and nonlinear demand[J].
European Journal of Operational Research, 2010, 207(3): 1321-1326.
DOI: 10.1016/j.ejor.2010.07.017. |
| [8] |
马利军. 具有公平关切成员的两阶段供应链分析[J].
运筹与管理, 2011, 20(2): 37-43.
MA Lijun. Supply chain analysis with fairness preference agent[J]. Operations Research and Management Science, 2011, 20(2): 37-43. |
| [9] |
林强, 魏光兴. 基于公平偏好的双渠道供应链改进回购契约协调[J].
物流技术, 2015, 34(1): 204-208.
LIN Qiang, WEI Guangxing. Study on improved buyback contract based coordination of bi-channel supply chains based on fairness preference[J]. Logistics Technology, 2015, 34(1): 204-208. |
| [10] |
成克河, 王磊, 王世伟. 具有公平关切参与者的双渠道供应链定价策略研究[J].
商业经济, 2013(4): 22-24.
CHENG Kehe, WANG Lei, WANG Shiwei. Pricing strategies of a dual-channel supply chain with participants of fairness preference[J]. Shangye Jingji, 2013(4): 22-24. |
| [11] |
杜少甫, 朱贾昂, 高冬, 等. Nash讨价还价公平参考下的供应链优化决策[J].
管理科学学报, 2013, 16(3): 68-80.
DU Shaofu, ZHU Jiaang, GAO Dong, et al. Optimal decision-making for Nash bargaining fairness concerned newsvendor in two-level supply chain[J]. Journal of Management Sciences in China, 2013, 16(3): 68-80. |
| [12] |
张克勇, 吴燕, 侯世旺. 讨价还价公平关切下闭环供应链差别定价策略[J].
工业工程, 2013, 16(6): 95-100.
ZHANG Keyong, WU Yan, HOU Shiwang. Differential pricing strategy of retailer's bargaining on concern of fairness in closed-loop supply chain[J]. Industrial Engineering Journal, 2013, 16(6): 95-100. |
| [13] |
SHI Y, ZHU J. Game-theoretic analysis for a supply chain with distributional and peer-induced fairness concerned retailers[J].
Management Science and Engineering, 2014, 8(1): 78-84.
|
| [14] |
覃燕红, 尹亚仙, 魏光兴. 公平偏好下基于Stackelberg博弈的回购契约研究[J].
工业工程, 2014, 17(4): 85-90.
QIN Yanhong, YIN Yaxian, WEI Guangxing. Stackelberg game based research on buy-back contract with fairness preference considered[J]. Industrial Engineering Journal, 2014, 17(4): 85-90. |
 2016, Vol. 19
2016, Vol. 19
